Tecnicas de conteo:
Tecnicas de conteo:
LAS TECNICAS DE CONTEO [br]Son aquellas que son usadas para enumerar eventos dificiles de cuantificar. La numeracion de puntos en un espacio muestral, en ocasiones es dificil y laboriosa por la cantidad de puntos a contar o enumerar. En este caso se recurre al analisis combinatorio, que es una manera mas sofisticada de contar.[br][br]PRINCIPIO FUNDAMENTAL DEL CONTEO[br][br]1.-Si un evento puede suceder o realizarse de "n" maneras diferentes y si, continuando el procedimiento un segundo ejemplo puede realizarse de "n1" maneras diferentes y asi sucesivamente, entonces el numero de maneras en que los eventos pueden realizarse en el orden indicado es el producto de "n1" * "n2" * "n3".....[br][br]REGLAS GENERALES DEL CONTEO [br]1-regla del producto(multiplicacion)-[br]--Si los eventos A y B pueden ocurrir de "m" y "n" maneras distintas respectivamente, entonces el total de maneras distintas en que ambos eventos pueden ocurrir en el orden indicado es "m" * "n".[br]Esta regla puede extenderse a tantos eventos como se quiera. El numero total de posibilidades es el producto del numero de posibilidades de cada evento. Por ejemplo, si los eventos "A", "B", "C" y "D" pueden ocurrir de "m", "n", "o" y "p" maneras distintas respectivamente, entonces el total de formas diferentes en que estos eventos pueden ocurrir en ese orden es, "m" * "n" * "o" * "p".[br][br] ~Ejemplo:[br]1.-Una persona para vestirse tiene la posibilidad de escoger entre 2 pares de zapatos, 3 pantalones y [br] 4 blusas ¿De cuantas maneras puede combinar las prendas?[br] SOLUCION: [br] Conocemos que hay 2 posibilidades de combinar los pares de zapatos (Z=2), los pantalones[br] de 3 maneras(P=3), y las blusas de 4(B=4).Entonces Z*P*B= 2*3*4= 24. Existen 24 [br] posibilidades de combinar las prendas.[br][br]2.-¿Cuantos juegos de placas de circulacion para automoviles pueden fabricarse, si se utilizan 3 digitos [br] y tres letras(en ese orden), si no se puede repetir ningun digito ni letra en cada placa, ni se puede [br] utilizar el cero, las letras O, Ñ y W.[br] SOLUCION:[br] Para el primer digito (D1) existen 9 posibilidades al quedar excluido el "0"; para el [br] segundo digito (D2) hay 8 alternativas, al no poder usar el "0" ni el usado en el primer [br] espacio; para el tercer digito (D3) quedan 7 posibilidades.Para la primera letra (L1),[br] se tienen 24 alternativas, ya que de las 27 letras del abecedario, 3 estan restringidas; [br] para la segunda letra (L2) se tienen 23 alternativas y para la letra (L3) quedan 22 [br] posibilidades, por lo que:[br] (D1)*(D2)*(D3)*(L1)*(L2)*(L3)= 9*8*7*24*23*22= 6120576. Se pueden fabricar [br] 6120576 juegos de placas con esas carcteristticas.[br][br]2.- REGLA DE LA SUMA[br][br] ~Si una primera tarea puede realizarse de "m" formas y una segunda tarea puede realizarse de "n" formas y no es posible realizar ambas tareas de manera simultanea entonces para realizar cualquiera de ellas pueden utilizarse cualquiera de "m"+"n" formas.[br][br] EJEMPLO:[br] 1.-Una biblioteca tiene 40 libros de historia y 50 de filosofia. Si un estudiante [br] quiere aprender acerca de alguno de estos dos temas, por la regla de la suma [br] puede elegir entre 40+50= 90 libros.[br] (NOTA: el estudiante no quiere estudiar historia y filosofia, sino historia o [br] filosofia)[br] La regla puede ampliarse a mas de dos tareas, siempre que ningún par de ellas [br] pueda ocurrir simultáneamente.[br][br][br]Permutaciones[br]~Las permutaciones de un numero "n" de objetos de un conjunto es cualquiera de las diferentes [br] maneras de ubicar esos objetos en un orden definido.[br] *Se utiliza el simbolo (nPn ó P(n) cuando se toman las permutaciones de igual [br] numero [img]https://static.xx.fbcdn.net/images/emoji.php/v9/t7d/1/16/1f44e.png[/img] de elementos u objetos del conjunto.[br]~Si se desean ordenar [img]https://static.xx.fbcdn.net/images/emoji.php/v9/t7d/1/16/1f44e.png[/img] objetos diferentes de una linea, el primer objetos se puede escoger de [img]https://static.xx.fbcdn.net/images/emoji.php/v9/t7d/1/16/1f44e.png[/img] maneras, el segundo de (n-1); y el tercero de (n-2) y asi, sucesivamente, hasta 1.[br][br]nPn= P(n)= (n)(n-1) (n-2)....(1)= n![br][br][br] EJEMPLOS:[br] ~ 1.-¿De cuantas maneras se pueden permutar los 3 digitos del numero 478?[br] SOLUCION:[br] P3=P(3)= 3*2*1= 3!=6[br] Las permutaciones son: 478, 487, 748, 784, 847 y 874.[br][br][br]Cuando las permutaciones se hacen de un tamaño (r) menor al numero [img]https://static.xx.fbcdn.net/images/emoji.php/v9/t7d/1/16/1f44e.png[/img] de elementos del conjunto, se utilizan indistintamente los simbolos (nPr) ó P(n,r).[br]De un grupo [img]https://static.xx.fbcdn.net/images/emoji.php/v9/t7d/1/16/1f44e.png[/img] de objetos, deseamos ordenar (r) objetos de una linea. El primer objeto se puede escoger de [img]https://static.xx.fbcdn.net/images/emoji.php/v9/t7d/1/16/1f44e.png[/img] maneras; el segundo de (n-1) y asi, sucesivamente, de manera que el ultimo de ellos sera (n-(r-1)= n-r+1.[br][br] 2.- ¿Cuantas permutaciones de 2 letras se puede formar a partir de las 5 vocales?[br] SOLUCION:[br] nPr= 5P3= n!/(n-r)! = 5!/(5-2)! = 5!/3!= 20.[br] [br] Las permutaciones son: ae, ai, ao, au, ea, ei, eo, eu, ia, ie, io, iu, oa, oe, oi, ou, ua, ue,[br] ui, uo.[br][br][br] 3.-¿ De cuantas maneras pueden sentarse 12 personas en una banca que solo tiene [br] capacidad para 7?[br][br] SOLUCION:[br] [br] nPr= 12P7= n!/(n-r)! =12!/5!= 3991680.[br][br] [br] CONTENIDO DEL CURSO DE MATEMATICAS DISCRETAS SOBRE PERMUTACIONES [br][br] 1.- PERMUTACIONE[br] A[br] B[br] C[br] D[br][br] 2.- PERMUTACIONES[br][br] ab ba ca da P1: elegir la 1° letra [br] ac bc cb db P2: elegir la 2° letra[br] ad bd cd dc hay 34*3= 12[br][br] 3.- PERMUTACIONES[br][br] P1: elegir la 1° letra 4*3*2=12 resultados [br] P2: elegir la 2° letra 3 permutaciones.[br] P3: elegir la 3° letra[br][br] 4.-PERMUTACIONES[br][br] P1: elegir la 1° letra.[br] P2: elegir la 2° letra. 4*3*2*1= 24.[br] P3: elegir la 3° letra 4 permutaciones posibles [br] P4: elegir la 4° letra.[br][br][br]
combinatoria
[br][br][br][img]https://probabilidadyestadisticabloque1.weebly.com/uploads/2/5/3/0/25308816/1980789_orig.jpg[/img][br]Es de interés, dada una cierta actividad, saber si existen resultados posibles. Si existen, ¿cuántos resultados posibles?, ¿cómo se clasifican?, ¿hay un algoritmo para clasificarlos?[br]Algunos resultados de la teoría de conjuntos, para conjuntos finitos. Si A y B son finitos entonces[br]|A| Cardinalidad de A o número de elementos. [br]Por ejemplo, A = {L, M, M, J, V, S, D}[br]|A| = 7[br][color=#ff00ff]Cardinalidad[/color][br]1. |AUB| = |A| + |B| -|A∩B|[br]2. SI A∩B = Ø entonces |AUB |= |A| + |B|[br]3. Si U es finito entonces |Ā|= |U|-|A| o bien |U| =|A|+|Ā|[br]4. Si A, B y C son finitos |AUBUC| = |A|+|B| +|C|-|A∩B|-|B∩C|-|A∩C|+|A∩B∩C|[br][color=#0000ff]Ejemplo 1[/color][br]La asistencia a dos partidos de futbol fue de 72397 personas al primer partido y de 69211 al segundo, en total 93478 asistieron a ambos juegos ¿Cuántos asistieron a ambos partidos?[br]Solución[br]|A|=72397, |B|=69211, |AUB|=93478[br]|AUB| = |A|+|B|-|A∩B|[br]=> |AUB|+|A∩B| = |A|+|B[br]=> |A∩B| = |A|+|B|-|AUB|[br]|A∩B| = |A|+|B|-|AUB|[br] = 72397 + 69211 - 93478[br] = 48130[br]48130 personas asistieron a ambos partidos.[br][color=#0000ff]Ejemplo 2[/color][br]Se encuestó a 98 estudiantes:[br]74 vieron la P1[br]57 vieron la P2[br]66 vieron la P3[br]52 vieron la P1 y P 2[br]51 vieron la P1 y P3[br]45 vieron la P2 y P3[br]43 vieron la P1, P2 y P3[br]¿Cuántas personas no vieron alguna de las 3 películas?[br]Solución[br]|U|=98[br]|P1|=74[br]|P2|=57[br]|P3|=66[br]|P1∩P2|=52[br]|P1∩P3|=51[br]|P2∩P3|=45[br]|P1∩P2∩P3|=43[br]|P1∩P2|- 43 = 52-43=9[br]|P1∩P3|- 43 = 51-43=8[br]|P2∩P3|- 43 = 45-43=2[br]|P1|-9-43-8=74-60=14[br]|P2|-9-43-2=57-54=3[br]|P3|-2-43-8=66-53=13[br]|AUBUC|=14+9+3+43+8+2+13=92[br]|U|-|AUBUC|=98-92=6[br]6 estudiantes no vieron ninguna película.[br]
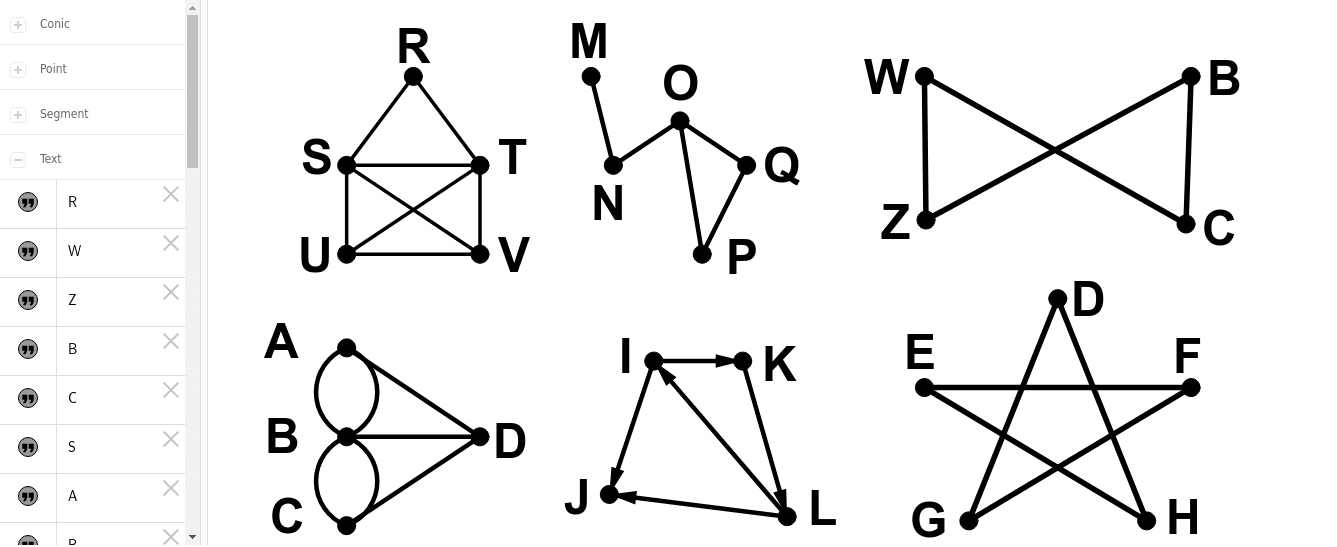
Collage de Grafos
ISOMORFISMO
ISOMORFISMO
[color=#9900ff]Isomorfismo [/color]de grafos Dados G=(V,E) y G´=(V´,E´), se denomina isomorfismo de G a G´ a la aplicación biyectivaf tal que para a,bÎV, {a,b}ÎE Û se cumple {f(a),f(b)}ÎE´. Es decir, la aplicación que relaciona biyectivamente pares de vértices de E con pares de vértices de E´, de modo que los vértices conectados por aristas siguen estándolo.[br]G y G´ se denominan isomorfos, y son [color=#9900ff]matemáticamente iguales[/color], solo varia la apariencia, o sea, que se mantienen las adyacencias, estructura, caminos y ciclos.[br][img width=567,height=139]http://www.dma.fi.upm.es/personal/gregorio/grafos/web/sucgraf_certifarboles/html/Isomorfismo%20de%20grafos_archivos/image002.jpg[/img][br]Los grafos G y G ‘ son isomorfos pues existe la biyección f: V ® V ‘ definida por f(a) = 2, f(b) = 1, f(c) = 3, f(d) = 4 que conserva la adyacencia.[br]ComplejidadLos problemas matemáticos se pueden dividir en primera instancia en dos grupos:[br] Problemas indecidibles: aquellos que no se pueden resolver mediante un algoritmo.[br] Problemas decidibles: aquellos que cuentan al menos con un algoritmo para su cómputo.[br]Sin embargo, que un problema sea decidible no implica que se pueda encontrar su solución, pues muchos problemas que disponen de algoritmos para su resolución son inabordables para un computador por el elevado número de operaciones que hay que realizar para resolverlos. Esto permite separar los problemas decidibles en dos:[br] intratables: aquellos para los que no es factible obtener su solución.[br] tratables: aquellos para los que existe al menos un algoritmo capaz de resolverlo en un tiempo razonable.[br]Los problemas pueden clasificarse también atendiendo a su complejidad. Aquellos problemas para los que se conoce un algoritmo polinómico que los resuelve se denominan clase P. Los algoritmos que los resuelven son deterministas. Para otros problemas, sus mejores algoritmos conocidos son no deterministas. Esta clase de problemas se denomina clase NP. Por tanto, los problemas de la clase P son un subconjunto de los de la clase NP, pues sólo cuentan con una alternativa en cada paso.[br]El problema de isomorfismo de grafos no se sabe si es un problema de la clase P o de la clase NP, y si hubiese una clase intermedia entre ambas, el isomorfismo de grafos sería el tipo de problema ideal para ella.[br]Existe un caso concreto de grafos (los árboles) donde el problema del isomorfismo si se puede resolver mediante la aplicación de algoritmos no muy complejos. Este caso será el que desarrollaremos en la segunda parte del proyecto, apartado 2.3.[br][br][br]Ejemplo:[br]Sean los siguientes grafos [b]G[sub]1[/sub][/b] y [b]G[sub]2[/sub][/b] [br] [img]http://mate.cucei.udg.mx/matdis/5gra/isomorfismo.gif[/img][br][br] Un isomorfismo para los grafos anteriores [b]G[sub]1[/sub][/b] y [b]G[sub]2[/sub][/b] esta definido por:[br][i]f[/i] (a) = A[br][i]f[/i] (b) = B[br][i]f[/i] (c) = C[br][i]f[/i] (d) = D[br][i]f[/i] (e) = E[br]y [i]g[/i](X[sub][i]i[/i][/sub]) = Y[sub][i]i[/i][/sub], [i]i[/i] = 1, ... , 5[br]Los grafos [b]G[sub]1[/sub][/b] y [b]G[sub]2[/sub][/b] son isomorfos si y solo si para alguna ordenación de vértices y lados sus matrices de incidencia son iguales. Veamos las matrices de incidencia de los grafos anteriores:[br][img width=515,height=160]http://mate.cucei.udg.mx/matdis/5gra/isomorfismo2.jpg[/img][br][br]Ejercicios:[br]Verificar si los siguientes pares de grafos son isomorfos.[br][br][br][br][br][br][img]http://mate.cucei.udg.mx/matdis/5gra/isomorfismo3.jpg[/img][br][b]a)[/b][br][img width=468,height=193]http://mate.cucei.udg.mx/matdis/5gra/isomorfismo4.jpg[/img]