Construcciones Geogebra en clase
En este libro GeoGebra tenemos una colección de actividades pensadas para llevar directamente al aula. Se ha procurado que sean actividades rápidas de hacer, para que podamos construirlas directamente en el ordenador mientras estamos en clase. Las actividades están agrupadas por bloques, introduciendo en cada una de ellas nuevos conocimientos para manejar el programa GeoGebra. Como complemento, se proponen algunos ejercicios de construcciones para practicar con las herramientas de GeoGebra. Enlaces [list] [*][url=https://www.geogebra.org/m/qympztcp]Construcciones preparadas[/url] para trabajar con los alumnos, agrupadas por curso y unidad.[/*] [*]Ejemplos de construcciones: [url=https://www.geogebra.org/m/ew8wdvd9]Geogebra en el aula.[/url][/*] [/list]
Table of Contents
- Geometría Plana
- Arcos de medio punto, escarzanos, de herradura, apuntados...
- Ejemplo de actividad de aula. "Situación de aprendizaje" Modelizado de arcos
- Polígonos
- Rectas tangentes
- Puntos de corte de dos tangentes a una circunferencia
- Ortocentro de los triángulos inscritos en una circunferencia
- Centros de los triángulos equiláteros inscritos en una cónica
- Polígonos y sus elementos
- Homotecias
- Ejercicios
- Ejercicios: Elementos Geométricos
- Ejercicio: Teorema de Napoleón
- Porisma de Poncelet. Polígonos bicéntricos; con circuncentro e incentro
- Arco de Navidad
- Cónicas. Aprendiendo GeoGebra.
- Ejercicio. Representación de intervalos
- Puntos a cierta distancia de un triángulo...
- Ejercicio. Propiedades de los cuadriláteros
- Modelizado paso a paso. Rosetón Parroquia San Gil Abad (Burgos)
- Elementos geométricos. Estela funeraria S. I a. C
- Funciones
- Ejemplo de actividad. Las temperaturas (funciones y exponenciales)
- Estudiar funciones
- Funciones a trozos
- Polinomio de interpolación
- Interpolación lineal
- Integral definida (Riemann)
- Desigualdades e inecuaciones
- Dos actividades rápidas con funciones
- Geometría del Espacio
- Gráficas en 3D
- Poliedros
- Superficies de Revolución
- Sólidos Platónicos
- Intersección de planos
- Perpendicular Común a dos rectas que se cruzan
- Modelado geométrico con Splines. Bellota
- Cilindros y superficies de revolución. Candy cane
- Realidad aumentada. Modelizado rápido de un depósito
- Montes y superficies de revolución. Cerro de Masatrigo
- Ejercicios (3D)
- Ejercicio. Creando un arbolito
- Ejercicio. Superficie en cilíndricas
- Cálculo simbólico CAS
- Operaciones con números
- Operaciones algebraicas
- Matrices
- Resolver ecuaciones
- Derivadas
- Integrales
- Límites y asíntotas
- Estadística y Probabilidad
- Estadísticas de 1 variable
- Regresión lineal
- Diagramas de Caja
- Problemas basados en la distribución Normal
- Problemas basados en la distribución Binomial
- Programación lineal
- LaTeX
- LaTeX en GeoGebra
- Nota. Podemos usar símbolos Unicode.
- Ejercicios de ampliación
- Rellenando un spline
- Arrastrar una parte de una función
- Visualizando la media de varios números
- Imágenes y transformaciones. Ejercicios
- Modelado geométrico y Resolución Numérica
- Ejercicios de estadística
- Actividades CAS para el aula. Ejemplos
- Triedro de Frênet. Usamos funciones paramétricas y sus derivadas.
- Gafas matemáticas. Uso de imágenes y LaTex
- Mirando con lupa...
- Espiral de Arquímedes
- Torre de Espantaperros y Prismas
- Flores-Polígonos regulares y ejes de simetría
- Conos y piedras de molino
Arcos de medio punto, escarzanos, de herradura, apuntados...
Los [url=http://enciclopedia.us.es/index.php/Arco_(arquitectura)]arcos[/url] de circunferencia son muy utilizados en construcciones. Los puntos en los que el arco se apoya el arco se llaman "impostas". La distancia entre las impostas se denomina "luz"[br][list][*]Los romanos solían utilizar medias circunferencias, y el arco se denominaba "de medio punto", de manera que el centro de la circunferencia está precisamente en la línea que une las impostas, y comprende un ángulo llano. Su altura es, precisamente, la mitad de su luz.[br][/*][*]Cuando el centro está por debajo de la línea de impostas, el arco se denomina "[url=https://es.wikipedia.org/wiki/Arco_escarzano]escarzano[/url]", y comprende un ángulo menor de 180º. Por tanto, es un arco rebajado (su[i] [/i]altura es menor que la mitad de su luz).[/*][*]Si el centro está por encima, el arco se denomina "de [url=https://es.wikipedia.org/wiki/Arco_de_herradura]herradura[/url]", y es un arco "ultrapasado" (altura mayor que la mitad de su luz).[/*][/list][br]
Arco de circunferencia que modeliza el arco escarzano "[url=https://cacereshistorica.caceres.es/patrimonio-historico/edificios-historicos/arquitectura-civil/arco-de-la-estrella-o-puerta-nueva/]Arco de la Estrella[/url]", en Cáceres.[br][br]Debajo, la imagen original (descargar para repetir esta construcción).[br][br][b]Ejercicio[/b]: buscar imágenes de otros arcos escarzanos, de medio punto o de herradura, y modelizarlos de la misma forma.
Arco de la Estrella, en Cáceres
Arco Carpanel de Tres Centros
Para disminuir el ángulo que forma el arco rebajado con las impostas, podemos añadir unas circunferencias tangentes tanto a ese primer arco como a los laterales. En particular, el centro de estos nuevos arcos debe estar en la línea de impostas.[br][br]Así, obtenemos un arco formado a su vez por tres arcos de circunferencia, que denominamos Arco Carpanel (de tres centros). En [url=https://www.geogebra.org/m/xttthtwe]este enlace[/url] puedes aprender más detalles sobre cómo crear este tipo de arcos.[br]En ocasiones, pueden añadirse más circunferencias.
Arco Carpanel en una casa
Imagen para modelizar
Arco típico en los pasillos de las casas de los pueblos de la Siberia Extremeña (España). Concretamente, Tamurejo.
Ejercicio. Fachada del CPR de Cáceres
La siguiente fotografía es de la fachada del CPR de Cáceres.[br]Podemos identificar diferentes elementos matemáticos, dependiendo de en qué nos interese centrarnos.[br]Analiza estos elementos utilizando GeoGebra.[br]Por ejemplo:[br][list][*]La pequeña rampa de entrada, combinada con los escalones, sirven para el estudio de la [b]pendiente de una recta[/b].[/*][*]Las propias escaleras, para analizar las rectas [b]paralelas[/b].[/*][*]El hecho de que la foto se tomó con un pequeño [b]ángulo[/b], hace que "sobre el papel", el ángulo de los laterales y las escaleras no sea del todo recto, pero ¿nos aporta información sobre el ángulo que estaba haciendo la cámara con la vertical respecto al suelo mientras se tomaba la fotografía?[/*][*]¿Qué figuras geométricas con las lámparas interiores? [/*][*]¿Y las piedras del contorno? Analiza qué herramientas matemáticas y de GeoGebra utilizaríamos para modelizarlas.[/*][/list]Pero queríamos centrarnos en el estudio de los arcos. Para ello, lo analizaremos de la siguiente manera:[br][list][*]¿Cómo trazar el primer arco de la izquierda? (describe matemáticamente, y llévalo a cabo)[br]Repite la actividad de manera que quede patente que es un arco de medio punto.[/*][*]El arco central, ¿es igual que el de la izquierda? ¿Qué estrategias matemáticas podemos llevar a cabo para mostrarlo?[/*][*]¿Y con el tercero?[/*][*]La parte superior del arco, ¿qué tipo de circunferencia formaría respecto la parte inferior?[/*][/list]
Entrada al CPR de Cáceres.
Comparando arcos
La siguiente imagen es del patio del edificio del Palacio de Toledo-Moctezuma de Cáceres, donde se encuentra el actual Archivo Histórico Provincial.[br][list][*]Podemos apreciar la diferencia entre un arco escarzano y uno de medio punto. Ambos tienen la misma flecha (altura), pero diferente luz (ancho). [/*][*]Añadiendo un poco más de curvatura en los extremos del arco escarzano, lo transformaríamos en un arco carpanel de tres centros.[/*][*]Vamos a observar las diferencias en la construcción. Compara las posiciones de los centros de las circunferencias y cómo varía el arco carpanel al modificar la posición del centro.[/*][/list][size=85](*) Recuerda que puedes visitar [url=https://www.geogebra.org/m/xttthtwe]esta actividad[/url] para aprender más sobre la construcción del arco carpanel.[/size]
Palacio de Toledo-Moctezuma
Otros arcos para modelizar
Aquí tienes otras imágenes que puedes utilizar para modelizar diferentes tipos de arco.[br][br]
Fachada de una casa de Siruela (Badajoz)
Una mirada matemática en la Plaza Alta de Badajoz
Las siguientes fotografías han sido tomadas en la Plaza Alta Marín de Rodezno, de Badajoz (España). [br][[url=https://goo.gl/maps/x5pXPBuPdDhv7Dp9A]Clic para ir a Google Maps[/url]]
Fachada de las Antiguas Casas Consistoriales de la Plaza Alta de Badajoz
Arco del Peso en la Plaza Alta de Badajoz
Al fondo, tras el arco, se ve la fachada del Convento de San José.
Convento de San José de Badajoz
Es habitual que combinar diferentes tipos de arco.
Ejercicios: Elementos Geométricos
Mediante comandos o las herramientas, podemos calcular perpendiculares, paralelas, mediatrices, bisectrices,... Por ejemplo:[br][list][*]Con [icon]https://www.geogebra.org/images/ggb/toolbar/mode_polygon.png[/icon] creamos un [b]triángulo[/b].[/*][*]Calculamos la [b]mediatriz[/b] de cada lado con [icon]/images/ggb/toolbar/mode_linebisector.png[/icon][/*][*]Marcamos su [b]intersección[/b] (circuncentro) con [icon]/images/ggb/toolbar/mode_intersect.png[/icon][/*][*]Trazamos la circunferencia circunscrita [icon]/images/ggb/toolbar/mode_circle2.png[/icon].[br][/*][/list]Por supuesto, la construcción es dinámica. Si movemos los puntos, todo se recalcula directamente.[br][br]Puedes probar a hacer la construcción [url=https://www.geogebra.org/geometry]aquí (https://www.geogebra.org/geometry)[/url].
Vídeos explicativos
En los siguientes vídeos veremos cómo construir con GeoGebra algunos de los elementos notables del triángulo:[br][list][*][url=https://drive.google.com/open?id=1RukQ6-SqCao2PfaFSiONNV_LSiiLk5wt]Medianas y baricentro[/url].[/*][*][url=https://drive.google.com/open?id=1wTJ2OULTzLILmQr7Z4q0phBlk5rfUKRp]Mediatrices, circuncentro y circunferencia circunscrita[/url].[/*][*][url=https://drive.google.com/open?id=14wbQo7NYWA0c37cvwuc84wLUQEDRSXOT]Alturas y ortocentro[/url].[/*][*][url=https://drive.google.com/open?id=1pLTvYfw4ChfcOqjnxCTMfXDsmlVaentY]Bisectrices, incentro y circunferencia inscrita[/url].[/*][/list]
Ejemplo de actividad. Las temperaturas (funciones y exponenciales)
Hemos decidido hacer un experimento casero, para ver cuántos minutos tarda en enfriarse el aceite de freir.[br][br]Usando un modelo matemático, [br]Ana ha calculado que sigue la función [math]f(t)=20+160\cdot 2^{-0.6t}[/math].[br]Juan, ha calculado que la función es [math]g(t)=20+160\cdot 10^{-0.18t}[/math].[br][br]1. Representa estas funciones, y haz una tabla de valores para ver las temperaturas.[br]2. Utiliza el siguiente applet para comprobar tus resultados.
Cuestiones
¿Conoces el número [i]e[/i]?[br]Pues resulta que hemos propuesto otro modelo, que es:[br][math]h(t)=20+160\cdot e^{-0.42t}[/math].[br][br][list][*]¿Resulta la misma función?[br][/*][*]Sabiendo que la cocina estaba a una temperatura ambiente de 20ºC,[br]¿qué relación crees que hay entre los coeficientes que aparecen en las funciones y la temperatura del aceite?[/*][*]¿Crees que hay alguna relación entre la base de la potencia y el coeficiente de [i]t[/i] que aparece en el exponente?[/*][/list]
Investiga
¿Qué podríamos decir de la siguiente función?[br][list][*][math]T(t)=30+150\cdot 3^{-0.49t}[/math][/*][/list]
Gráficas en 3D
Superficie paramétrica
Crear una superficie introduciendo su forma paramétrica solo nos supondrá una línea:[br][list][*][b]Superficie(a,b,sen(a) sen(b),a,-10,10,b,-10,10)[/b][/*][/list]Pruébalo en la [url=https://www.geogebra.org/classic/3d]vista 3D (https://www.geogebra.org/classic/3d)[/url]
Ejercicio. Creando un arbolito
Nuestro primer árbol
Aprovecharemos los objetos 3D de GeoGebra para crear un árbol tipo "cono".[br]Por comodidad, haremos que la altura del tronco y de la copa sean variables. Para ello, usaremos las siguientes instrucciones:[br][quote][code]altura1 = 3[br]altura2 = 6[br]circ1: Circunferencia((0, 0), 1)[br]tronco: Cilindro(circ1, altura1)[br]circ2: Circunferencia((0, 0, altura1), 3)[br]copa: Cono(circ2, altura2)[br][/code][/quote][br]Una vez cambiados los colores y la opacidad, el resultado debería ser similar al siguiente:
Observa y responde
[list=1][*]En la construcción, fíjate que GeoGebra ha añadido algunos objetos auxiliares, como puede ser el vértice del cono.[/*][*]Edita la definición (propiedades) de la segunda circunferencia. Verás que GeoGebra ha modificado lo que nosotros introdujimos, reescribiéndolo como[br][quote][code]circ2: Circunferencia((0, 0, altura1), 3, planoXY)[/code][/quote][/*][/list]Indica a qué crees que se deben estas dos cosas.
Modificando nuestro arbolito
Vamos a añadir una segunda copa al árbol, y modificar un poco los colores.[br]Para ello, usaremos los siguientes comandos:[br][quote][code]altura3 = 4[br]circ3: Circunferencia((0, 0, altura1 + altura2 / 2), 2)[br]copa2: Cono(circ3, altura3)[/code][/quote]Una vez modificados los colores, el resultado debería ser similar al siguiente:[br][br][br]
Ejercicio
De forma similar a como hemos hecho anteriormente, modifica nuestro arbolito, incluyendo una tercera copa y cambiando los colores.[br]Intentaremos obtener un resultado similar al siguiente:
¿Cómo lo hemos hecho?
Indica, a continuación, cuáles han sido los comandos que has introducido para crear esta tercera copa.
Sólido de rotación
Si nos fijamos, también era posible definir nuestro arbolito como un sólido de rotación, tanto el tronco como la copa.[br]Como el tronco ha sido sencillo de modelizar con un cilindro, veamos cómo hacer la copa:[list][*]En primer lugar, borramos u ocultamos las copas anteriores, para crear la nueva.[/*][*]A continuación, haremos una poligonal en el plano y=0. Si queremos, podemos representarlo, como se ha hecho en el applet de más abajo.[/*][*]Los puntos de la poligonal podrían ser:[br][quote][code]A = (3, 0, altura1)[br]A0 = (1, 0, altura1)[br]B = (2, 0, altura1 + altura2 / 2)[br]B0 = (1.3, 0, altura1 + altura2 / 2)[br]C = (1.5, 0, altura1 + altura2 / 2 + altura3 / 2)[br]C0 = (0.8, 0, altura1 + altura2 / 2 + altura3 / 2)[br]D = (0, 0, altura1 + altura3 + altura4)[/code][/quote][/*][*]Crearemos la poligonal con el comando:[br][quote][code]perfil = Poligonal({A0, A, B0, B, C0, C, D})[/code][/quote][/*][*]Por último, el sólido de revolución se crea con el comando [url=https://wiki.geogebra.org/es/Comando_Superficie]Superficie[/url], en el que hay que incluir el ángulo de giro (2pi, o 360º para una vuelta completa), y el eje de rotación si no es el eje X. [/*][*]Podemos utilizar una variable para ese ángulo. En este caso, la denominaremos [code]ang[/code]. El comando para crear la superficie será:[br][quote][code]copaRotacion = Superficie(perfil, ang, EjeZ)[/code][/quote][/*][/list]Una vez modificados los colores, y animando el ángulo, la construcción podría quedar como en el siguiente applet. [br]
Operaciones con números
Los comandos son completamente intuitivos, (y también tenemos herramientas, como [icon]/images/ggb/toolbar/mode_factor.png[/icon]). [br]Algunos ejemplos:[br][list][*]Factoriza[360][/*][*]FactoresPrimos[42][/*][*]ListaDivisores[15][/*][*]MCD[12, 15][/*][*]MCD[{12, 30, 18}][/*][*]MCM[12, 15][/*][*]MCM[{12, 30, 18}][/*][/list][br]Puedes probar estos comandos en el modo [url=https://www.geogebra.org/classic/cas]cálculo simbólico CAS (https://www.geogebra.org/classic/cas)[/url]
Estadísticas de 1 variable
GeoGebra incorpora una potente hoja de cálculo que podemos usar para hacer todo tipo de estadísticas.[br]Además el modo [url=https://www.geogebra.org/spreadsheet]hoja de cálculo (https://www.geogebra.org/spreadsheet)[/url] tiene preprogramadas las funciones que necesitaremos más habitualmente, usando el [b]botón de análisis de una variable[/b] [icon]/images/ggb/toolbar/mode_onevarstats.png[/icon].
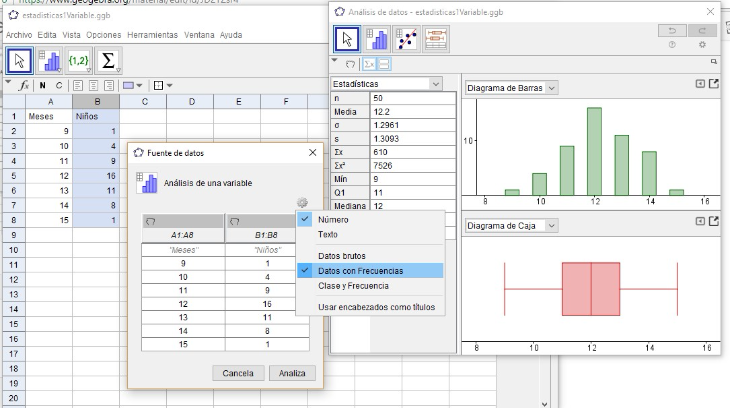
Ejemplo
Un pediatra obtuvo la siguiente tabla sobre los meses de edad de 50 niños de su consulta en el momento de andar por primera vez.[br][list=1][*]Haz el diagrama de caja y bigotes correspondiente.[br][/*][*]Calcula la media y la desviación típica.[br][/*][/list]
LaTeX en GeoGebra
LaTeX también en rótulos
Se puede utilizar LaTeX en los rótulos (por ejemplo de los botones) o dentro de las listas desplegables.[br]Tan solo hay que poner el comando entre símbolos de dólar que es lo que se ha hecho en el botón "Fórmulas [math]\textcolor{brown}{\sqrt{x},\frac{a}{b}}[/math]" , cuyo rótulo es (dólar)\text{Fórmulas \textcolor{brown}{\sqrt{x},\frac{a}{b}}(dólar)
Para más información, visitar la [url=https://wiki.geogebra.org/es/Sobre_LaTeX_-medidas_de_fuentes_-_cajas_de_color_y_matem%C3%A1tica_-]wiki de GeoGebra[/url] sobre LaTeX, o la recopilación de ejemplos [url=https://www.geogebra.org/m/RC7Pnnk5]https://www.geogebra.org/m/RC7Pnnk5[/url], de [url=https://www.geogebra.org/u/michael+borcherds]Michael Borcherds[/url].[br][br]Más nombres de colores en [url=https://en.wikibooks.org/wiki/LaTeX/Colors#The_68_standard_colors_known_to_dvips]este enlace (wikibooks)[/url]. Para usar los colores predefinidos LaTeX, podría hacerse así: \textcolor{ProcessBlue}{Hola}[br][br]En este [url=https://oeis.org/wiki/List_of_LaTeX_mathematical_symbols]enlace de oeis.org[/url] hay una lista de los principales símbolos matemáticos en LaTeX.[br]
Rellenando un spline
Un [url=https://wiki.geogebra.org/es/Comando_Spline?lang=eu]Spline[/url] es una curva suave que une varios puntos.[br]GeoGebra tiene la particularidad de que si cambiamos su opacidad (al elegir el color), rellenará el interior del Spline.[br]Vamos a probarlo:[br][list][*]Introducimos varios puntos A,B,C,D,E en la vista gráfica, con la herramienta punto [icon]/images/ggb/toolbar/mode_point.png[/icon]. [/*][*]Creamos el Spline con el comando [b]Spline({A, B, C, D, E}, 3)[/b][/*][*]Lo seleccionamos, y modificamos su color y su opacidad con los botones de la barra de herramientas.[/*][/list]