MTH 4/583 Midterm Exam Fall 2017
Instructions:
[u]1. You are welcome to write out your responses on paper or to type your responses in a different program![/u][br]I really only need a geogebra file through Question 2, and it may be easiest to create a new geogebra file instead of typing into this one. To get the link for a Geogebra file, first choose "Sharing" from the menu.[br]2. Please name your file as: LastName_FirstName_MTH4583_Winter2017 . [br]When you are finished, save the file a last time and upload a file containing the link (as well as any other links or files) to the midterm folder on the D2L dropbox. [br]

Task 1
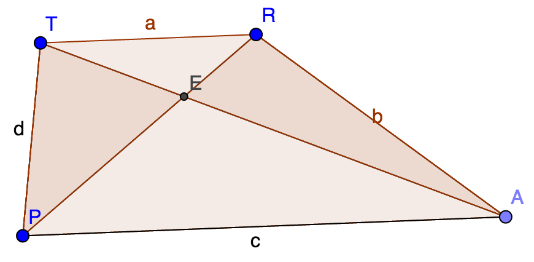
Construct a (non-isosceles) trapezoid TRAP. Construct the diagonals and label their intersection E (see figure).
Exam Question 1
What is the "drag test"? Employ and describe the results of the "drag test" in relation to the figure you constructed above.
Exam Question 2
Go back to your construction, and now construct the height h of the trapezoid through E (e.g., the perpendicular to TR and PA). Label the height of triangle PEA [math]h_1[/math] and the height of triangle TER [math]h_2[/math]. What can you say about the ratio [math]\frac{h_1}{h_2}[/math] in terms of a, b, c, or d? [br]
Exam Question 3
Write the area of the trapezoid in terms of [math]h_1[/math] and [math]h_2[/math].
Exam Question 4
Use your responses above to explain why triangle PET and triangle EAR must have the same area.
Exam Question 5
Find a primitive Pythagorean triple with hypotenuse 73. Explain how the geometry of the complex plane can be used to find the primitive triple.
Exam Question 6
Suppose that x can be written as the sum of two squares, and y can be written as the sum of two squares. Prove that xy can be [i]also [/i]be written as the sum of two squares. Hint: how can you use complex numbers to write the sum of two squares as a product?[br][br][br]
Exam Question 7
Use polynomial division to find the equation of a [b][i][color=#ff0000]parabola[/color][/i][/b] that is tangent to the function [math]f\left(x\right)=x^4-2x^3+3[/math] at [math]x=1[/math] and [math]x=0[/math] . Form and articulate (at least) two conjectures about relationships between roots, remainders, and tangency behavior.[br]