
Fonctions Linéaires et Affines - Introduction(3e)
Activité - Aide aux consignes
[color=#9900ff][b]Pour chacune des parties, déplacer éventuellement les figures/points et faire varier les paramètres (curseurs) sur les figures qui suivent, et répondre aux questions.[/b][br][/color]
Voici 2 programmes de calculs

Etude des deux programmes (Introduction)
[b][color=#0000ff][u]Selon vous, quelle est la différence principale entre ces deux programmes de calcul?[/u][/color][/b][br]
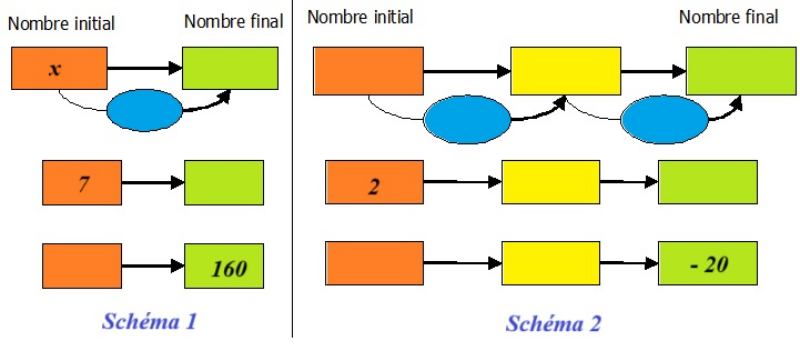
[b][color=#0000ff][u]Une des deux fonctions peut s’écrire sous la forme [i]x→ ax[/i]. [/u][/color][/b][color=#0000ff][u][color=#0000ff][u]Ce type de fonction est appelé une [/u][/color][/u][/color][b][color=#0000ff][u][b][color=#0000ff][u]fonction [i]linéaire. [/i][/u][/color][/b]Quelle est-elle ? Que vaut a?[/u][/color][/b]
Etymologie
[size=85][justify][size=100][color=#0000ff][size=200][size=150]"[u]Linéaire[/u]" : [/size][/size][/color][size=200][size=150][i]xv[sup]e[/sup] siècle. Emprunté du latin linearis, de même sens.[br]Qui a rapport aux lignes ; qui se fait par des lignes. Mesure linéaire, mesure de longueur. Le mètre est l’unité de mesure linéaire. Dessin linéaire, représentation des objets par un simple trait. Mouvement linéaire, qui suit une ligne droite[/i][/size][/size][color=#0000ff][size=200][size=150].[br][br]"[u]Affine[/u]" [/size][/size][/color][size=200][size=150][i]xx[sup]e[/sup] siècle. Emprunté du latin affinis, « limitrophe, voisin ; allié », lui-même dérivé de finis, « limite, fin, but »[/i][/size][/size][color=#0000ff][size=200][size=150].[br]Image : Mathovore[/size][/size][/color][br][/size][br][/justify][/size]
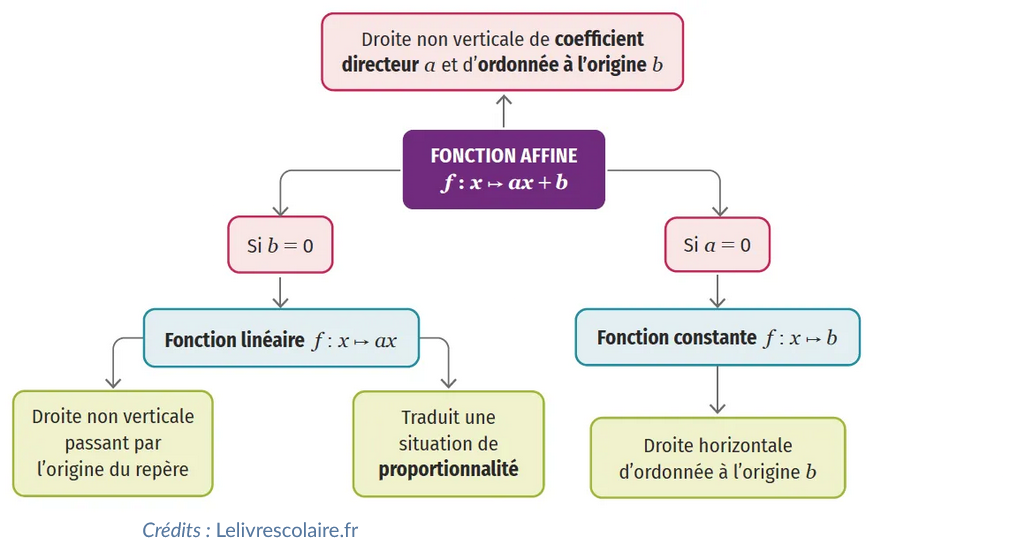
[b][color=#0000ff][u]L’autre fonction peut s’écrire sous la forme [b][i]x → ax + b[/i][/b] où [b][i]a[/i][/b] et [b][i]b[/i][/b] sont des nombres fixes. [/u][/color][/b][color=#0000ff][u][color=#0000ff][u]Ce type de fonction est appelé[/u][/color][/u][/color][b][color=#0000ff][u][b][color=#0000ff][u] une fonction [i]affine. [/i][/u][/color][/b]Préciser alors les valeurs correspondantes de[b][i] a[/i][/b] et [b][i]b[/i][/b].[/u][/color][/b]
Compléter le tableau (1) de valeurs de la fonction f
Compléter le tableau (2) de valeurs fonction g
[color=#0000ff][b]Quelle particularité possède le tableau(1), et que ne possède pas le tableau (2) ?[/b][/color]
Représentation graphique des fonctions f et g
[b][color=#0000ff]Quelle est la représentation graphique d'une fonction linéaire? affine? [br]Quelle semble être la différence entre les deux?[/color][/b]
(A faire sur le graphique précédent)
[color=#9900ff][b]Avec l'onglet curseur , Construire un curseur a (il suffit de sélectionner l'onglet et cliquer sur la[br]feuille de travail. Appliquer les valeurs ci-contre: min=− 5 max = 5 incrément = 0,5[br]Créer un deuxième curseur b.[br]Entrer dans la barre de saisie: f(x)=a*x+b[br]Construire le point d'intersection de la droite avec l'axe des ordonnées, puis faire apparaître ses coordonnées.[/b][/color]
Tableaux de valeurs (vertical)
[b][color=#0000ff]On cherche ici à construire le tableau de valeurs de la fonction affine f telle que[i] f[/i]([i]x[/i][i])= 2[/i][i] x[/i][i]− 4[/i][br]a) Dans B2, entrer la formule :[i] =[/i]2*A2 - 4 puis valider.[br]b) Incrémenter (étirer) cette formule jusqu’en B13.[/color][/b]
[b][color=#0000ff]c) Pour cette fonction f telle que f(x) = 2x - 4[br]A l'aide du tableau, recopier et compléter : [i]f[/i](3) = ….. [i]f[/i](0) = ……… [i]f[/i](……) = 0 [i]f[/i](……) = − 12[/color][/b]
[b][color=#0000ff]d) Quelle formule de tableur serait inscrite en B13? [/color][/b]
[b][color=#0000ff]e) De la même manière, compléter le tableau de valeurs ci-dessous de la fonction affine g telle que[i] [br]g[/i]([i]x[/i][i])= -5[/i][i]x +9[/i][br][i]x[/i] varie pour des valeurs entières comprises entre – 7 et 4.[/color][br][/b][br]
[b][color=#0000ff]f) Pour cette fonction g telle que g(x) = - 5x+ 9[/color][/b][b][color=#0000ff][br]A l’aide du tableau, compléter : [i]g[/i](− 2) = ….. [i]g[/i] (0) = ……… [i]g[/i](……) = 0 [i]g[/i](……) = 6[/color][/b]
[b][color=#0000ff]g) Lorsque [i]x[/i] augmente de1, de combien varie son image ? A quoi correspond ce nombre ?[/color][/b][br][br][br]
[img]https://i.ytimg.com/vi/ni1cSNtLgWY/maxresdefault.jpg[/img][br][color=#9900ff][size=200][b][i][u][size=85]crédit image : mathlab[/size][br]Cas général[/u][/i] : Une fonction est affine, elle est de la forme [i]f[/i] ([i]x[/i][/b] ) = [b][i]a[/i][/b] [b][i]x[/i][/b] + [b][i]b[br][/i][/b][br][b][i]f[/i][/b] (0) correspond au nombre [i][b]b [/b](Vérifier cela dans les deux exemples précédents[/i].)[br][br]Lorsque [b][i]x[/i][/b] augmente de 1, son image augmente de [b][i]a[/i][/b][/size][/color]
[size=200][center][b][color=#ff0000]Bilan vidéo + learning app[/color][/b][/center][/size]