Distribuciones de probabilidad
Veremos algunas de las distribuciones más usuales y su relación De forma genérica hay dos tipos: discretas y continuas
Table of Contents
- Distribución binomial
- Distribución Binomial
- Distribución normal
- Distribución normal
- Relación Binomial-normal
- Aproximación de la Binomial a la normal
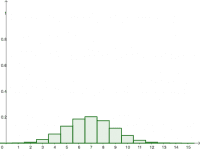
Distribución Binomial
Binomial
La distribución de probabilidad binomial es una distribución discreta en la que queremos calcular la probabilidad de r éxitos cuando repetimos. el experimento n veces. El experimento se denomina dicotómico, es decir o tenemos éxito con una probabilidad p, o fracasamos con probabilidad 1-p (también se llama de Bernouilli)[br][math]P\left(X=r\right)=\binom{n}{r}p^r·\left(1-p\right)^{n-r}[/math]
Si acumulamos la probabilidad de ocurrencia de un nº de éxitos, es decir[br][math]P\left(X\le r\right)=\sum_{k=0}^rP\left(X=k\right)[/math][br]Se llama función de distribución de la probabilidad
Prueba a:
- Varía la probabilidad y comprueba como cambia la distribución de probabilidad[br]- Varía el nº de repeticiones y verás como cambia la configuración[br]- Fíjate que en última instancia el valor acumulado es de 1
Distribución normal
Campana de Gauss
La. distribución de variable normal, es la distribución de probabilidad de una variable continua, la más usual. [br]La función de densidad tiene una forma acampanada, de ahí su nombre y la expresión es:[br][math]f\left(x\right)=\frac{!}{\sqrt{2\pi}\sigma}e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}}[/math]
Función de distribución
Se definer como:[br][math]F\left(a\right)=P\left(X\le a\right)=\int_{-\infty}^af\left(x\right)dx[/math][br]Por tanto es el área encerrada por la curva y el eje OX, hasta la variable, ese área es la probabilidad
Aproximación de la Binomial a la normal
Condiciones
En determinadas condiciones se puede aproximar la Binomial a la normal:[br][*][b][img]data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACH5BAEAAAAALAAAAAABAAEAAAICRAEAOw==[/img]np≥5 [/b]El número esperado de éxitos es al menos 5.[/*][*][b][img]data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACH5BAEAAAAALAAAAAABAAEAAAICRAEAOw==[/img]n(1−p)≥5[/b] El número esperado de fracasos es al menos 5.[/*][*][b][img]data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACH5BAEAAAAALAAAAAABAAEAAAICRAEAOw==[/img]n≥30 [/b] Un número de ensayos (n) grande facilita la aproximación.[/*]
Recordar que la media y la desviación típica de la bonomial son:[br]Media: [math]\mu=n·p[/math][br]Desviación típica: [math]\sigma=\sqrt{n·p·\left(1-p\right)}[/math][br]Por tanto la normal aproximada tendrá una distribución[br][math]N\left(n·p,\sqrt{n·p·\left(1-p\right)}\right)[/math][br]Puedes comprobar usando los deslizadores en qué condiciones es mejor o peor aproximación