[b][i][size=200][center]ESTIMACIÓN DE ÁREAS DE CUADRADOS, RECTÁNGULOS Y TRIÁNGULOS EN EL GEOPLANO[/center][/size][/i][/b]

Para esta actividad la vamos a dividir en dos casos[br]A) [u]Cuando uno de los lados es paralelo o perpendicular a las filas del geoplano[/u]. [size=85](imágenes 01 y 02)[/size][br]B) [u] Cuando sus lados son oblicuas (inclinadas) respecto al geoplano.[/u] [size=85](imágenes 03 y 04)[/size][br]

[b]A)[/b] [i][size=150][b]Cuando una de los lados es paralelo o perpendicular a las filas del geoplano. [/b][/size][/i]

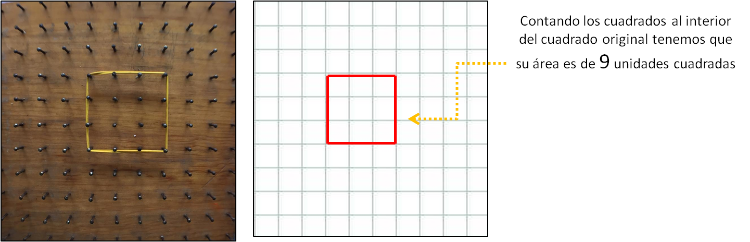
 [b]ACTIVIDAD 04[/b][b][b].-[/b][/b] Cuando tenemos a un cuadrado o a un rectángulo, para estimar su área basta con contabilizar las unidades cuadradas (los cuadrados) que hay en él, veamos el siguiente el ejemplo.

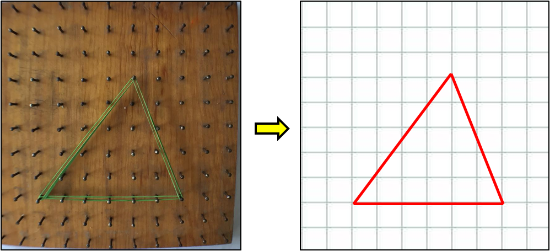
 [b][b][b]ACTIVIDAD 05[/b][b][b].-[/b][/b][/b][/b] Cuando tenemos un triángulo, no es de la misma manera.

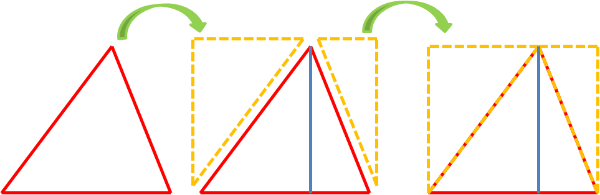
[br][br]Dado el triángulo, a partir del lado que esta sobre la malla del geoplano,  trazamos:[br][list][*]la altura  del triángulo [size=85](segmento azul)[/size][/*][*]construimos el rectángulo (o cuadrado) circunscrito a él, con altura igual a la altura del triángulo [/*][/list]

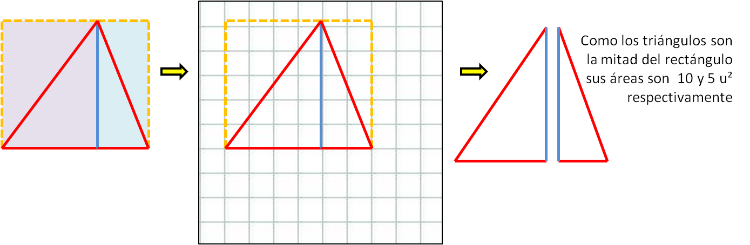
[list][*]A partir de la altura del triángulo, el rectángulo que formamos se puede dividir a su vez en dos[br]rectángulos con la particularidad de que los lados del triángulo original son[br]diagonales de cada uno de ellos. [/*][*]Contando los cuadrados al interior de cada rectángulo tenemos que sus áreas son de 20 y 10 u² respectivamente[br][br][br][/*][/list]