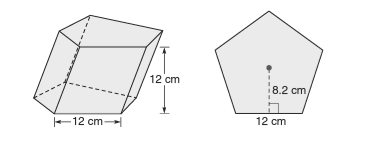
[b]Para los ejercicios 41-43 considere el prisma pentagonal regular oblicuo que se muestra. Cada lado de la base mide 12 cm y la altura mide 12 cm.[br][br] 42. Encuentre el área total del prisma. [/b]

[color=#ff0000]1. Analizamos y establecemos los datos dados en el problema [/color][br]Datos [br]Base: 12 cm [br]Altura: 12 cm [br]Apotema: 8.2 cm [br][br][color=#ff0000]2. Primeramente, debemos encontrar el área lateral de un prisma pentagonal regular oblicuo, es igual al perímetro por la altura. [/color][br][br]a) Encuentre el área lateral del prisma.[br][br][math]A_{_{_L}}=P\times h[/math][br][math]A_{_{_L}}=12cm\left(5\right)\times12cm[/math][br][math]A_{_{_L}}=60cm\times12cm[/math][br][math]A_{_{_L}}=720cm^2[/math][br][br][color=#ff0000]3. El área total de un prisma es igual a la suma de su área lateral (área de sus caras laterales) y el área de sus dos bases.[/color][br]El área de la base es igual al perímetro por el apotema dividido entre dos[br][br][math]A_B=\frac{P\times a}{2}[/math][br][math]A_B=\frac{60cm\times8.2cm}{2}[/math][br][math]A_B=246cm^2[/math][br][br][b]42) Encuentre el área total del prisma.[/b][br][br][math]A_T=A_L+2A_B[/math][br][math]A_T=720cm^2+2\left(246cm^2\right)[/math][br][math]A_T=720cm^2+492cm^2[/math][br][math]A_T=1212cm^2[/math][br][br]