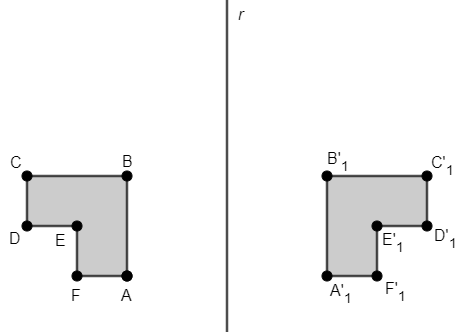
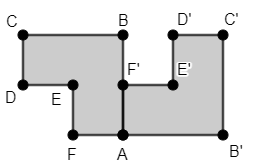
Uma transformação geométrica no plano é uma função [i]T [/i]que associa cada ponto [i]P[/i] de seu domínio um ponto [i]P'[/i] no seu contradomínio, dado por [i]T(P) = P' [/i]que é denominado imagem de [i]P[/i] pela transformação [i]T[/i].[br]Entre essas transformações, identificamos as que são denominadas transformações isométricas - rotação, reflexão e translação - como as que preservam distâncias entre pontos. A imagem de um polígono por meio de uma transformação isométrica é um polígono congruente ao original, ou seja, com seus ângulos preservados e, também, perímetro e área. Na homotetia, uma transformação não isométrica, a distância entre pontos não necessariamente é preservada. A imagem de um polígono por meio de uma homotetia poderá não ser um polígono congruente ao polígono original mas, sim, um polígono semelhante. [br][br]

Transformações isométricas são transformações geométricas que preservam as distâncias entre os pontos, ou seja, que não alteram o tamanho ou a forma, apenas sua posição no espaço podendo preservar ou não a orientação dos objetos. Exemplos de transformações isométricas: translações, reflexões e rotações.