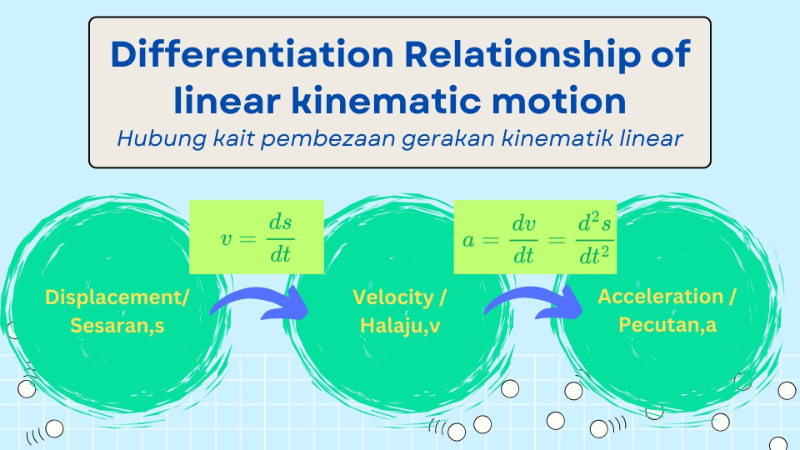
8.2 Differentiations in Kinematics of Linear Motion
[justify][size=100]Differentiation in linear kinetic motion refers to the mathematical process of determining the rate of change of motion-related quantities, such as displacement, velocity, and acceleration, with respect to time. These rates are foundational in understanding the dynamics of objects in linear motion.[b] The differentiation always starts from displacement, s=f(x). [/b][/size][i][size=100][br][br][/size][/i]The [b]velocity[/b] is defined as [b]the rate of change of displacement with respect to time[/b]. Hence, the velocity function,v is given by:[/justify][center][br][math]v=\frac{ds}{dt}[/math][br][br][/center][justify][size=100]The[b] acceleration[/b] is [b]the rate of change of velocity with respect to time[/b]. Hence, the acceleration function,a is given by:[br][/size][/justify][i][center][math]a=\frac{dv}{dt}=\frac{d^2s}{dt^2}[/math][/center][/i][justify][br]The relationship between the displacement function, s, the velocity function, v, and the acceleration function, a, can be summarized as shown in the following diagram:[/justify]
