
Tópicos de Geometria
Relembrando
Apresentando aqui um resumo de alguns conceitos estudados em geometria plana, para que você possa recordá-los e aplicá-los, sempre que necessário, neste estudo de geometria espacial.
Ângulos
[b]Ângulos complementares e ângulos suplementares[br][/b] Dois ângulos são complementares se, e somente se, a soma de suas medidas é 90°. Um deles é o complemento do outro.[br] Dois ângulos são suplementares se, e somente se, a soma de suas medidas [br]é 180°. Um deles é o suplemento do outro.[br][br][b] Ângulo nulo e ângulo raso[br][/b] Pode-se estender o conceito de ângulo para se ter o ângulo nulo (cujos lados são coincidentes) ou o ângulo raso (cujos lados são semirretas opostas).[br] Então, a medida [b][i]a [/i][/b]de um ângulo é tal que [math]0°\le a\le180°[/math]
Observe:

Os ângulos complementares
Os ângulos complementares são os ângulos cuja soma equivale a 90°. Esses ângulos estão compreendidos entre 0° e 90°.[br]Dois ângulos complementares que compartilham um mesmo lado e um vértice entre eles, são chamados de adjacentes.[br]Além disso, não existem pontos que são comuns a região compreendida dos ângulos adjacentes.
Os ângulos AÔC e BÔC são complementares e adjacentes cuja soma é 90°.
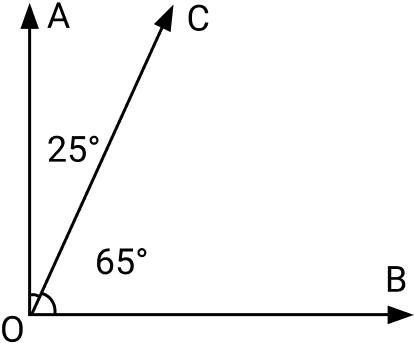
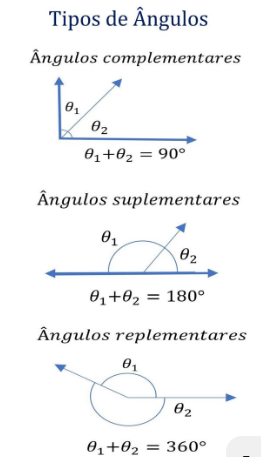
Os [url=https://matematicabasica.net/angulos/]ângulos[/url] complementares são os ângulos que a soma das medidas dos dois ângulos equivale a 90°. Enquanto que os ângulos suplementares a soma das medidas dos ângulos equivale a 180°. Já os ângulos replementares, a soma das medidas equivale a 360°.
Retas paralelas - definição

Retas paralelas cortadas por uma transversal
Euclides propôs que a condição para que duas retas sejam paralelas é uma reta transversal, não perpendicular, que corta às duas formando ângulos alternados congruentes.[br][br][br] Essa proposição de Euclides pode ser visto na imagem a seguir:[br][br][br][img width=343,height=244]https://matematicabasica.net/wp-content/uploads/2019/02/retas-paralelas-2-1.png[/img][br] Seja duas retas r e s, paralelas entre si e uma transversal t, não perpendicular a r e s. [br][br] Temos que os 8 (oito) ângulos formados pela reta transversal com as retas r e s, quatro deles serão agudos (α) e congruentes (mesma medida), os outros quatro serão obtusos (β) e congruentes. [br][br] Além disso, os ângulos obtusos e agudos serão suplementares (medem 180°).[br][br] Os ângulos β (beta) tem medidas iguais, assim como os ângulos α (alfa). E a soma de α + β é 180°, dessa forma eles são suplementares.[br][br] Os ângulos formados pelas retas paralelas com a transversal são nomeados como: ângulos correspondentes, alternos e colaterais
Observe
Ângulos Correspondentes:[br] Os [url=https://matematicabasica.net/angulos/]ângulos[/url] correspondentes são aqueles que possuem as mesmas medidas e ocupam a mesma posição. Na imagem os ângulos α e β, além de ocuparem a mesma posição, são congruentes.[br][br][img width=343,height=241]https://matematicabasica.net/wp-content/uploads/2019/02/retas-paralelas-3-1.png[/img][br][br][br]Ângulos Alternos:[br] Os ângulos alternos são os ângulos que estão em lados opostos. Os ângulos α e β estão em lados diferentes da reta transversal. Além disso, os ângulos alternos são congruentes. Eles também podem está dentro ou fora das retas r e s.[br][br][img width=343,height=470]https://matematicabasica.net/wp-content/uploads/2019/02/retas-paralelas-4-1.png[/img][br][br]Ângulos Colaterais:[br] Os ângulos colaterais são aqueles que estão do mesmo lado da reta transversal, mas em posições diferentes. Eles não são congruentes. Porém, são suplementares, ou seja, a soma das suas medidas é igual a 180°.[br][img width=343,height=241]https://matematicabasica.net/wp-content/uploads/2021/09/retas-paralelas-5-1.png.webp[/img]
Exercícios Resolvidos sobre retas paralelas
1) Encontre os valores para x e y que corresponde as medidas dos ângulos na figura:[img]https://matematicabasica.net/wp-content/uploads/2019/02/retas-paralelas-8.png[/img][br]Resolução:[br][br]Ao analisar a imagem percebe-se que x e 60° são ângulos alternos. Em retas paralelas cortadas por uma transversal os ângulos alternos são congruentes. [br][br]Portanto, x = 60°[br][br]O ângulo ao lado de y é correspondente ao ângulo de 60°, dessa forma podemos encontrar a medida de y assim:[br][br]Como y e 60° são suplementares, a soma deles mede 180°.[br][list][*]y = 180° – 60° = 120°[/*][/list]

O Teorema de Pitágoras
O Teorema de Pitágoras é um dos mais famosos teoremas da matemática. Este teorema é aplicado aos comprimentos dos lados do [url=https://matematicabasica.net/triangulo-retangulo/]triângulo retângulo[/url] — triângulo que possui um ângulo reto, isto é, que mede 90°.[br][br]O Teorema de Pitágoras diz que: “O quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos”.[br][br] A hipotenusa é o lado do triângulo que tem a maior medida e fica oposta ao ângulo reto, enquanto os catetos existem dois: o cateto adjacente e o cateto oposto. [br] O cateto adjacente é aquele que fica ao lado de um ângulo e o cateto oposto fica em frente a um determinado ângulo. Veja no triângulo abaixo:[br][br][img width=308,height=167]https://matematicabasica.net/wp-content/uploads/2019/02/triangulo-retangulo-1-1.png.webp[/img][br][br][br]Hipotenusa: a hipotenusa é o lado que fica oposto ao ângulo reto.[br][img width=321,height=163]https://matematicabasica.net/wp-content/uploads/2019/02/teorema-de-pitagoras-hipotenusa-1.png[/img][br][br][br]Cateto Oposto: o cateto oposto fica oposto a um dos ângulos.[br][img width=307,height=150]https://matematicabasica.net/wp-content/uploads/2019/02/teorema-de-pitagoras-cateto-oposto-1.png[/img] [br][br][br]Cateto Adjacente: o cateto adjacente fica ao lado de um dos ângulos.[br][img width=290,height=166]https://matematicabasica.net/wp-content/uploads/2019/02/teorema-de-pitagoras-cateto-adjacente-1.png.webp[/img][br][br][br]Fórmula do Teorema de Pitágoras:[br] O teorema de Pitágoras diz que a soma dos quadrados dos catetos é igual à hipotenusa ao quadrado. Isso pode ser traduzido em uma fórmula:[br]a² = b² + c²[br]Onde:[br][list][*]a: representa a hipotenusa;[/*][*]b e c: representa os catetos oposto e adjacente.[/*][/list]Exemplo:[br]Considere um triângulo com as seguintes medidas:[br][list][*]Hipotenusa: 5 cm[/*][*]Cateto Adjacente: 4 cm[/*][*]Cateto Oposto: 3 cm[/*][/list][br][br][br]Aplicando o Teorema de Pitágoras, a soma dos quadrados dos catetos tem que ser igual à medida da hipotenusa ao quadrado, assim: a² = b² + c²[br][br]Então: 5² = 3² + 4² ⇒ 25 = 9 + 16 ⇒ 25 = 25[br] Podemos ver isso na imagem abaixo, onde temos 9 quadrados no cateto oposto e 16 no cateto adjacente. Somando-se os quadrados dos catetos, chegamos a soma dos quadrados que estão na hipotenusa.[br][br][br][br][img width=536,height=530]https://matematicabasica.net/wp-content/uploads/2019/02/teorema-de-pitagoras-2-1.png.webp[/img][br][br][br]Pitágoras provou que a área dos quadrados construídos sobre os lados de um triângulo retângulo referente aos catetos, equivale à área do quadrado construído ao lado da hipotenusa.[br]
Exercícios Resolvidos:
Calcule a medida da hipotenusa para o triângulo retângulo ABC, com ângulo reto em B, sendo que os catetos AB e BC, têm medidas de 6 cm e 8 cm, respectivamente.[br][img width=353,height=183]https://matematicabasica.net/wp-content/uploads/2019/02/teorema-de-pitagoras-3-1.png[/img][br][br]Cálculos dos quadrados dos catetos:[br][list][*](AB)² = 6² = 36 cm[/*][*](BC)² = 8² = 64 cm[/*][/list]Aplicando o Teorema de Pitágoras, temos:[br][list][*](AC)² = (AB)² + (BC)²[/*][*]x² = 36 + 64, com x > 0 ⇔ x² = 100 ⇔ x = √100 ⇔ x = 10 cm[/*][/list][br][br][br]Calcule a medida do cateto AB do triângulo retângulo ABC, com ângulo reto em B, sabendo que a hipotenusa AC tem medida igual a 10 cm, e o cateto BC mede 5 cm.[br][br][img width=353,height=183]https://matematicabasica.net/wp-content/uploads/2019/02/teorema-de-pitagoras-4-1.png[/img]Cálculo do quadrado da hipotenusa AC e do cateto BC:[br][list][*](AC)² = 10² = 100 cm[/*][*](BC)² = 5² = 25 cm[/*][/list]Aplicando o Teorema de Pitágoras, temos:[br][list][*](AC)² = (BC)² + (AB)²[/*][*]100 = 25 + x², com x > 0 ⇔ x² = 100 – 25 ⇔ x² = 75 cm ⇔ x = √75 ⇔ x = 5√3 cm[/*][/list]
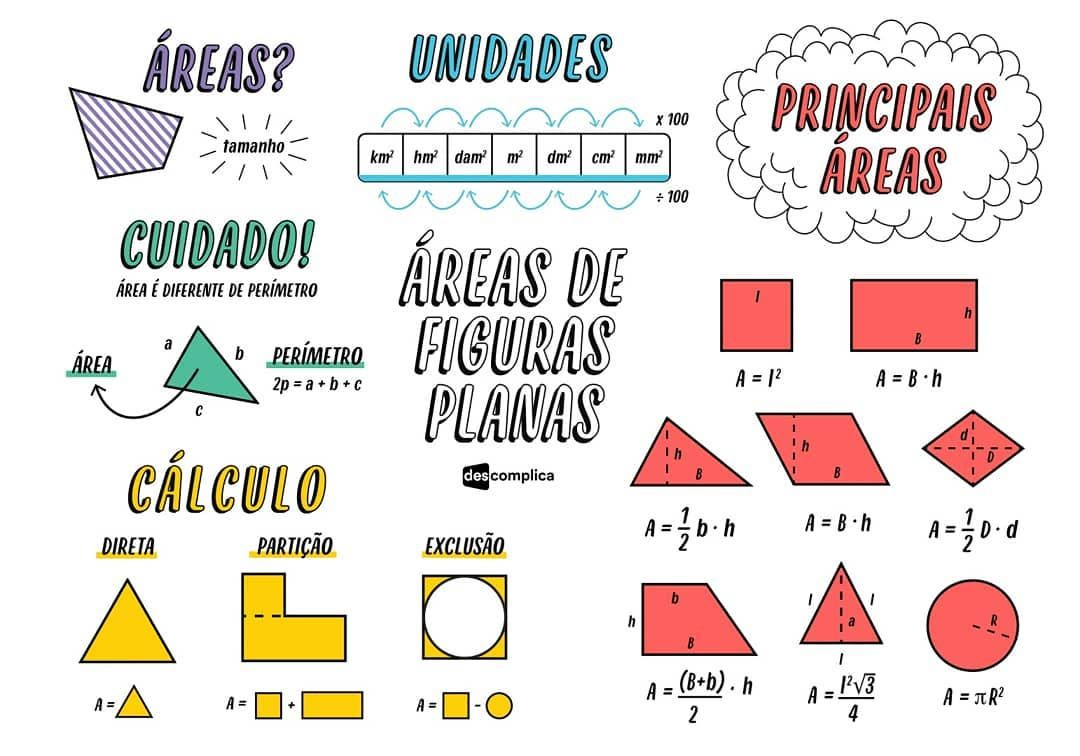
Área de figuras planas
Prismas
Consideremos um Quadrilátero qualquer ABCD condito num plano [i]a [/i]e um segmento XY de uma reta concorrente com [i]a[/i].
Um prisma é um sólido geométrico que possui duas bases congruentes e paralelas, que são polígonos, e faces laterais que são paralelogramos. Por exemplo, um prisma pode ter uma base quadrada e faces laterais retangulares.[br][br]Em termos de conhecimentos prévios, é importante entender conceitos básicos de geometria, como áreas de polígonos, propriedades de paralelogramos e operações com figuras tridimensionais.[br][br]As aplicações dos prismas são diversas e frequentemente encontradas em situações do cotidiano e na indústria, tais como:[br][br][list=1][br][*][b]Embalagens e caixas[/b]: Muitas caixas e embalagens são modeladas como prismas retangulares ou prismas hexagonais para otimizar espaço e facilitar o armazenamento e transporte.[br][br][/*][br][*][b]Arquitetura[/b]: Alguns edifícios possuem estruturas de telhados que podem ser modeladas como prismas, especialmente em áreas industriais e comerciais.[br][br][/*][br][*][b]Óptica[/b]: Prismas são essenciais em óptica para dispersão de luz e análise espectral, como os prismas usados em espetroscopia para separar a luz em seus componentes de comprimento de onda.[br][br][/*][br][*][b]Educação[/b]: São frequentemente utilizados como exemplos para ensinar conceitos geométricos básicos e propriedades de figuras tridimensionais para estudantes.[br][/*][/list]
Classificação e Tipos de:
Figura geométrica criada pela união de retas congruentes[br][br] O prisma é uma das várias [url=https://www.maisbolsas.com.br/enem/matematica/formas-geometricas-planas-e-espaciais]formas geométricas[/url]. É formado pela união de faces laterais paralelas, com base de mesma forma e tamanho (congruentes). Os prismas são classificados a partir de como suas bases são estruturadas, podendo ser denominado de quadrangular, triangular, pentagonal e outros. [br][br] Conheça abaixo as características dos prismas, as divisões, elementos e fórmulas. [br] [br] A Geometria Espacial[br][br]A geometria espacial é a área da matemática que estuda as figuras ou formas geométricas que ocupam um lugar no espaço, ou seja, que possui três dimensões (altura, largura e comprimento).[br]As principais figuras geométricas espaciais são as apresentadas abaixo:[br][br]• Tetraedro;[br]• Dodecaedro;[br]• Octaedro;[br]• Icosaedro;[br]• Pirâmide;[br]• Cubo;[br]• Prisma.[br][br]Nomenclatura dos prismas:[br] Um prisma é identificado pela forma como a base é estruturada. Pode ser:[br]• Quadrangular: é o prisma com base em forma de quadrado;[br]• Triangular: a base tem o formato de um triângulo. Rampas e telhados angulares são exemplos de prismas presentes no cotidiano;[br]• Hexagonal: sua base em formato de hexágono (seis lados). É encontrado nas "cabeças” de porcas e parafusos;[br]• Pentagonal: a base é um pentágono (cinco lados). O Pentágono nos Estados Unidos é a construção mais famosa nesse formato;[br]• Heptagonal: é o prisma com base em heptágonos (sete lados);[br]• Octagonal: a base do prisma é formada por octógonos (oito lados).[br][img]https://images.educamaisbrasil.com.br/content/banco_de_imagens/mb/D/tipos-de-prismas.jpg[/img][i]Tipos de prismas (Imagem: Mais Bolsas) [br][br][/i][br]Elementos de um prisma Um prisma é composto por alguns elementos. [br] São eles:[br][br]• Bases: são os lados congruentes e paralelos da figura. Representado por R e S na figura abaixo;[br]• Altura: é a menor distância entre as bases. Na figura baixo é representado pela distância h dos planos a e ß;[br]• Arestas das bases: são os lados das bases de um polígono. No prisma indicado é representado por (AB), (BC), (CD), (DE), (EA), (A' B' ), (B'C'), (C'D'), (D' E' ), (E'A');[br]• Arestas laterais: são os lados das fases que não pertencem a base. São os seguimentos (AA'), (BB'), (CC'), (DD'), (EE') na figura abaixo;[br]• Faces laterais: são os paralelogramos. São os seguimentos (AA'BB'), (BB'C'C), (CC'D'D), (DD'E'E), (EE'A'A) na forma abaixo.[br][img]https://images.educamaisbrasil.com.br/content/banco_de_imagens/mb/D/elementos-de-um-prisma.jpg[/img][i]Elementos que formam um prisma. (Imagem: Mais Bolsas) [br][br][/i][br]Classificação dos prismas:[br] Um prisma poderá ser diferenciado pela sua inclinação. Assim, eles podem ser reto, regular ou oblíquo. [br]• Prismas retos: são aqueles em que as arestas laterais são perpendiculares aos planos das bases. A medida da altura será igual à medida das arestas;[br][img]https://images.educamaisbrasil.com.br/content/banco_de_imagens/mb/D/prisma-reto.jpg[/img][i]Prisma reto. (Imagem: Mais Bolsas)[/i][br]• Prismas oblíquos: são aqueles em que as retas laterais formam ângulo de 90º com o plano das bases; [br][img]https://images.educamaisbrasil.com.br/content/banco_de_imagens/mb/D/prisma-obliquo.jpg[/img][i]Prisma oblíquo. (Imagem: Mais Bolsas) [/i][br]• Prisma regular: é o prisma reto no qual a base é um polígono regular. Para ser considerado prisma regular é necessário que todos os lados tenham a mesma medida e os ângulos internos sejam congruentes entre si. [br][img]https://images.educamaisbrasil.com.br/content/banco_de_imagens/mb/D/classificacao-dos-prismas.jpg[/img][i]Classificação dos prismas. (Imagem: Mais Bolsas)[/i][br]