[color=#ff0000][size=150]UTILIZZARE DEI PARAMETRI[br][/size][/color]Vediamo in questi primi esperimenti l'utilità di usare delle lettere al posto dei numeri. Se vogliamo posizionare un punto in una certa posizione sarà sufficiente specificare le sue coordinate [math]\large{x}[/math] e [math]\large{y}[/math], ma una volta stabilita la sua posizione rimarrà lì...[br][br][b]Che fare se invece vogliamo poter spostare il punto in seguito, o vogliamo che si muova in un certo modo - quindi, in entrambi i casi vogliamo riservarci la possibilità di [i]cambiare[/i] le sue coordinate?[/b] [br][br]Nei prossimi esperimenti vediamo come una lettera può essere utilizzata come contenitore, un segnaposto - [i]placeholder[/i] in Inglese - che possiamo poi riempire con contenuti via via diversi.[br][br][b]RICORDA[/b]: per aggiungere un punto scrivi le sue coordinate (in forma numerica.. o algebrica) tra parentesi tonda e separate da una virgola [p.e.: [color=#ff0000]A=([/color]3, 7[color=#ff0000])[/color]]

[b][color=#ff0000]RICORDA[/color][/b]: per creare un segmento usa la funzione "segmento(<punto>, <punto>)" [p.e. per tracciare un segmento dal punto (2,4) al punto A - che deve essere già presente per essere riconosciuto - [color=#ff0000]segmento([/color](2,4)[color=#ff0000],[/color] A[color=#ff0000])[/color]]

[b]Sfida aggiuntiva: [/b]Aggiungi dei segmenti che si muovano in verso opposto a quelle che hai creato: ad esempio in s[sub]2[/sub] dovrà partire dal fondo quando a=0 e muoversi verso l'alto, In s[sub]1[/sub] dovrà partire da destra e andare verso sinistra e così via[br][color=#ff0000][br][/color][b][br]RICORDA[/b]: puoi aggiungere un poligono con la funzione "poligono(, ..., )" [p.e. [color=#ff0000]poligono([/color](2,3)[color=#ff0000], [/color](6, 3)[color=#ff0000],[/color] (4,4)[color=#ff0000])[/color]

[b]Sfida aggiuntiva 1[/b]: l'altezza della piattaforma può essere cambiata tramite un parametro h (ma il numero dei gradini rimane costante[br][br][b]Sfida aggiuntiva 2[/b]: Il numero dei gradini può essere cambiato (da 3 a 6) tramite un parametro n (ma l'altezza della struttura e la larghezza dei gradini rimane costante).

[size=150][color=#ff0000]QUANTI MODI CI SONO PER UNIRE DUE PUNTI?[br][/color][/size]Nell'animazione sotto vogliamo che il punto H si muova sulla[color=#c27ba0][b] rotaia viola[/b][/color] al cambiare del [color=#e69138]parametro [b]a[/b][/color]. Quanti modi ci sono per generare questo movimento? [br][br][b]Prova a giocare con lo slider p[/b]. Cosa cambia? come è possibile ottenere questi effetti secondo te?

[b][color=#0000ff]Suggerimento:[/color][/b] Come abbiamo visto nei primi esempi, vogliamo che ad[color=#ff0000] a=0 corrisponda un'altezza di H pari a 1[/color], mentre ad [color=#0000ff]a=3 deve corrispondere un'altezza h=5[/color]. Possiamo rappresentare queste due coppie come punti: [math]\large{\textcolor{red}{A(0,1}}[/math] e [math]\large{\textcolor{blue}{B(3,5)}}[/math].[br][br]ci sono tanti modi per unire questi due stati, tanti quanti ce ne sono di unire i corrispondenti punti...

[b][color=#ff0000]RICORDA![/color][/b] Puoi inserire dei connettori logici in geogebra utilizzando i simboli[br][br][table][tr][td]&&[/td][td]per il connettore logico AND - [math]\large{\land}[/math][/td][/tr][tr][td]| |[/td][td]per il connettore logico OR - [math]\large{\lor}[/math][/td][/tr][/table]

Ed ora proviamo a divertirci aggiungendo un po' di movimento...

Abbiamo imparato cosa sono seno e coseno, finalmente non siamo più condannati a muoverci sempre diritto![br][br]Accogli le sfide dei prossimi esperimenti, ricordati che:[br][list][*]per inserire un punto è sufficiente inserire le sue coordinate all'interno di parentesi tonde. Ad esempio per inserire un punto di coordinate [math]\large{x=3}[/math] e [math]\large{y=5}[/math] è sufficiente scrivere [b][color=#0000ff](3,5)[/color][/b].[/*][*]le funzioni goniometriche in Geogebra si chiamano [b][color=#0000ff]sin()[/color][/b], [b][color=#0000ff]cos()[/color][/b] e [b][color=#0000ff]tan()[/color][/b][/*][*]queste funzioni misurano gli angoli in RADIANTI, quindi vanno da [math]\large{0}[/math] a [math]\large{2\pi}[/math] (cioè da [math]\large{0}[/math] a [math]\large{\approx 6,28}[/math]); [math]\large{\pi}[/math] si indica con la sigla [b][color=#0000ff]pi[/color][/b], quindi ad esempio 60° si indica come [color=#0000ff][b]pi/3[/b][/color].[/*][/list]

[b][color=#ff0000]ALCUNI SUGGERIMENTI PER I PROSSIMI ESERCIZI[/color][/b] [br][list][*]per assegnare un nome ad un punto che vuoi creare, in modo da potervi far riferimento in seguito, premetti alle coordinate del punto la lettera maiuscola del nome ed il segno di uguale. Esempio: [b][color=#0000ff]C=(2,1)[/color][/b][br][/*][*]una volta che hai creato i punti che ti servono, puoi creare un segmento che unisce due punti con l'istruzione [b][color=#0000ff]segmento(A,B)[/color][/b], dove [math]\large{A}[/math] e [math]\large{B}[/math] sono i nomi dei due estremi del segmento che vuoi creare.[br][/*][/list]

Per il prossimo esercizio ti potrebbe far comodo fare riferimento alle coordinate di certi punti nelle tue formule. [b][color=#ff0000]RICORDA[/color][/b]: con Geogebra è sufficiente scrivere [math]\large{x(Z)}[/math] per indicare la coordinata [math]\large{x}[/math] del punto [math]\large{Z}[/math].

Viene data una funzione [math]\Large{f(x)}[/math]. [br][br]Usando questa come riferimento, si costruisce la funzione [math]\Large{g(x)}[/math] come indicato nell'animazione qui sotto.

Ovviamente puoi utilizzare lo slider per vedere l'effetto; consideriamo ora però, a titolo di esempio, il valore iniziale dato al parametro [b]k[/b], cioè [b]k=3[/b]. [br][br]La funzione [math]\Large{g(x)}[/math] punto per punto "va a prendere" il risultato che [math]\Large{f(x)}[/math] ha [b]3[/b] unità più avanti.[br]Se sulle [math]\Large{x}[/math] abbiamo il tempo, è come se [math]\Large{g(x)}[/math] "anticipasse" di tre unità il comportamento di [math]\Large{f(x)}[/math][br][br][code]Il risultato di g nel punto x coincide con il risultato di f nel punto...[/code][br][br]Come può essere espressa quindi [math]\Large{g(x)}[/math]?

Che significato pratico ha questa scrittura? [br][br]Puoi facilmente ricavare che l'equazione di [math]\Large{f}[/math] è [math]\Large{f(x)=x^2-10x+16}[/math][br][br]Come fai a trovare il risultato di [math]\Large{f(x)}[/math] nel punto [math]\Large{x=3}[/math]? E nel punto [math]\Large{x=-2}[/math]?[br][br]Quindi come fai a trovare, data una qualsiasi [math]\Large{x}[/math], a trovare il valore che [math]\Large{f(x)}[/math] assume [b]tre unità più avanti rispetto a [math]\Large{x}[/math][/b]?[br][br]Svolgi i conti ed inserisci l'espressione che ottieni nell'animazione sotto, iniziando con [code]g(x)=...[/code]

[b][color=#0000ff]UNA PREMESSA: FACCIAMO IL PUNTO SUGLI STRUMENTI[code][/code][/color][/b][code][br][/code]Per lavorare in questa pagina avrai bisogno di costruire funzioni, ed in particolari funzioni definite a tratti. A questo scopo Geogebra mette a disposizione due istruzioni:[br][br][list][*][color=#38761d][b]VERSIONE 1:[/b][/color] Se(Condizione, Allora)[br][br][/*][*][b][color=#0000ff][/color][color=#bf9000]VERSIONE 2:[/color][color=#0000ff] [/color][/b]Se(Condizione, Allora, Altrimenti)[br][br][/*][/list][b][color=#38761d]La prima versione[/color][/b] controlla [code]Condizione: [/code]quando è vera restituisce [code]Allora[/code][code][/code], altrimenti [u]non dà nessun risultato[/u] - quindi [color=#ff0000]quando [/color]la [code]Condizione[/code][code][/code] è falsa [color=#ff0000]il risultato della funzione [/color][color=#ff0000]non è definito[/color].[br][br]Ad esempio se scriviamo[br][br][code]y = Se(-2<x<3, 4+2x)[/code][br][br]otteniamo una funzione che SE x è compresa tra -2 e 3 restituisce 4+2x, altrimenti non è definita - la funzione non esiste fuori da questo intervallo. In termini matematici equivale ad una funzione definita a tratti... con un solo tratto![br][br][math]\large{ y=2x+4 \qquad \{-2\lt x \lt 3\} }[/math][br][br]La funzione è riprodotta nell'animazione qui sotto.[br][br]

[b][color=#b45f06]la seconda versione[/color][/b] di questo comando ci permette di costruire situazioni più articolate: se [code]Condizione[/code] è vera restituisce [code]Allora[/code], quando invece [code]Condizione[/code] è falsa il risultato è [code]Altrimenti[/code]. Ad esempio se dobbiamo riprodurre la funzione definita a tratti[br][br][math]\large{y=\begin{cases}x+3&\qquad x\lt2\\5-x&\qquad x\ge2 \end{cases}}[/math][br]potremmo provare a scrivere [br][br][code]y=se(x<2, x+3, 5-x)[/code][br][br]Vedi il risultato qui sotto

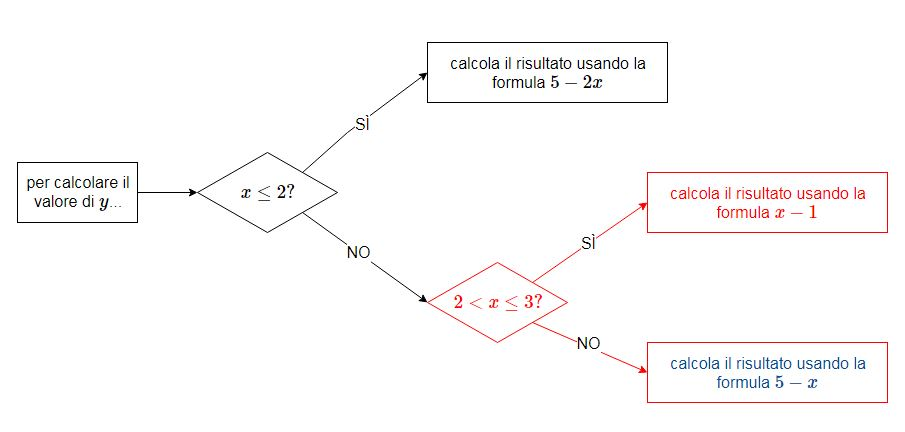
Per ottenere risultati ancora più articolati è possibile [b][color=#b45f06]innestare una dentro l'altra più funzioni del secondo tipo[/color][/b]. Ad esempio per ottenere[br][br][math]\large{y=\begin{cases}5-2x&\qquad x\le 2 \\ x-1&\qquad 2\lt x\le 3\\5-x&\qquad x\gt3\end{cases}}[/math][br][br]Possiamo utilizzare una combinazione del tipo[br][br][math]\large{\mbox{Se}(x\lt=2\ ,\ 5-2x,\ \textcolor{red}{\mbox{Se}(2\lt x \lt = 3,\ x-1,\ \textcolor{blue}{5-x})})}[/math] [br][br]La [math]\large{y}[/math] viene calcolata in questo modo: se [math]\large{x\le 2}[/math] (primo intervallo), verrà utilizzata l'espressione [math]\large{5-2x}[/math] [color=#ff0000]altrimenti fa un ulteriore controllo: se è vera [math]\large{\textcolor{red}{2\lt x\le 3}}[/math] (secondo intervallo) calcoleremo la [math]\large{\textcolor{red}{y}}[/math] tramite l'espressione[/color] [math]\large{\textcolor{red}{x-1}}[/math], [color=#0000ff]altrimenti (terzo intervallo) useremo la formula[/color] [math]\large{\textcolor{blue}{5-x}}[/math].[br]

[color=#ff0000][b]Quando si utilizza una tecnica di questo tipo è importante controllare che le funzioni siano innestate correttamente: ogni nuovo Se svolge il ruolo dell'Altrimenti per il Se precedente; inoltre ogni parentesi che viene aperta deve essere chiusa nel punto opportuno[/b][/color].[br][br]Qui sotto vedi la funzione; come al solito puoi cliccare sulla sua espressione per verificare come è fatta.

Si può innestare un numero qualsiasi di controlli uno dentro l'altro, ottenendo così funzioni costituite da un qualsiasi numero di tratti. [br][b][br][color=#38761d]Per vedere alcuni esempi di funzioni costruite in questo modo fa riferimento all'applet qui sotto, che puoi cliccare ed ispezionare a piacere[/color][/b].

[size=150][color=#ff0000]LE FUNZIONI COME LEGAME TRA UN INPUT ED UN OUTPUT[/color][/size][br]Abbiamo definito una [b][color=#ff0000]funzione[/color][/b] come un particolare tipo di [color=#ff0000][b]connessione tra due insiemi, che per ogni elemento di partenza, o [i]input,[/i] restituisce un risultato, o [i]output[/i][/b][/color]. Una delle applicazioni più frequenti di questo tipo di strumento è la possibilità di stabilire la [i]legge[/i] con cui definiamo come deve comportarsi un certo elemento.[br][br]Vediamo un semplice esempio.[br][br]Supponiamo di avere una macchina in cui c'è un disco verde. Noi vogliamo che una volta che la macchina sia accesa il disco sia[br][list][*]in una certa posizione [b][color=#0000ff]per i primi due secondi[/color][/b], ad esempio nel punto [math]\large{\textcolor{blue}{(-1,4)}}[/math] in un certo sistema di riferimento[/*][*]in un'altra posizione [b][color=#38761d]per i tre secondi successivi[/color][/b], ad esempio nel punto [math]\large{\textcolor{#ff7700}{(-1,0)}}[/math][br][/*][/list][br][ipotizziamo che dopo cinque secondi il ciclo ricominci]. [br][br]L'animazione sotto usa una funzione per impostare questo comportamento:[br][list][*]la variabile [math]\large{\textcolor{red}{t}}[/math], libera di cambiare da 0 a 5, simula il tempo che passa - e quando attiveremo l'animazione [premendo sulla freccia nell'angolo in basso a sinistra del piano cartesiano] SARÀ il tempo che passa.[/*][*]la funzione [math]\large{\textcolor{#007700}{f}}[/math], definita a tratti, restituisce come risultato [math]\large{\textcolor{blue}{4}}[/math] quando l'input è minore o uguale di 2, e [math]\large{\textcolor{#ff7700}{0}}[/math] quando l'input è compreso tra 2 e 5. Proprio come serve a noi![/*][/list][br][b]A questo punto è fatta![/b] Usiamo la variabile [math]\large{ \textcolor{red}{t}}[/math] come input della funzione [math]\large{\textcolor{#007700}{f}}[/math] e prendiamo [math]\large{\textcolor{#007700}{f(t)}}[/math], il risultato che ci restituisce la funzione (e che abbiamo modellato come vogliamo noi), per usarlo come coordinata [math]\large{y}[/math] del nostro disco verde.[br][br][center][math]\Large{ \textcolor{red}{t} \underrightarrow{\text{\small{\ dato t, f restituisce\ \ }}} \textcolor{#007700}{f(t)} \underrightarrow{\text{\small{\ il risultato f(t) è usato da \ \ }}} A(0,\textcolor{#007700}{f(t)}) }[/math][/center][br][br]Nota: Geogebra permette di [b]animare[/b] gli slider, facendo cambiare automaticamente la posizione del cursore e quindi il valore della variabile. Questa opzione ci sarà utile per definire funzioni il cui output deve cambiare in funzione del [b]tempo[/b].

Sia la coordinata [math]\large{x}[/math] che la coordinata [math]\large{y}[/math] del punto dipenderanno dal parametro [math]\large{a}[/math]. Definisci l'espressione di [math]\large{a}[/math] che, dato un certo valore di questo parametro, permette di calcolare la corrispondente coordinata [math]\large{x}[/math] del punto [math]\large{A}[/math]. Dovrebbe essere abbastanza semplice. Poi definisci l'espressione che calcola la coordinata [math]\large{y}[/math] del punto in funzione del valore di [math]\large{a}[/math]. Costruisci un punto le cui coordinate sono date da queste due espressioni... ed il gioco è fatto!

[b]NOTA:[/b] se necessario quando lo slider del tempo è visibile puoi anche trascinarlo manualmente per verificare accuratamente le caratteristiche del modo del punto secondo per secondo.

Generalizziamo ora il concetto. Vogliamo costruire un punto che percorra in continuazione il rettangolo riportato nell'animazione qui sotto, partendo da puunto A e muovendosi in senso antiorario.[br][br]Supponiamo che il punto si muova alla velocità di 1 quadretto al secondo. [br][br][list][*]costruisci uno slider t la cui estensione sia pari al tempo necessario al punto per compiere un intero giro. Nelle opzioni dello slider (accessibili con il tasto destro) specifica che dovrà muoversi in modo crescente. [/*][*]definisci la funzione a(t) che restituisca, dato un qualsiasi istante t, il valore che dovrà avere la coordinata x del punto[/*][*]definisci la funzione b(t) che restituisca, dato un qualsiasi istante t, il valore che dovrà avere la coordinata y del punto[/*][/list][br]A questo punto costruisci il punto usando le funzioni a(t) e b(t).[br]

[b][color=#ff0000]UNA VARIANTE IMPEGNATIVA[/color][/b][br]Ecco una sfida per toccare con mano quanto il concetto di funzione può rendere flessibile ogni tua creazione. Crea uno slider [b]v[/b] che vada da 1 a 4: indicherà la velocità del punto (1= un quadretto al secondo, 4=quattro quadretti al secondo). [br][br]Come devi modificare le tue funzioni in modo che cambiando il valore di v il punto si muova di conseguenza? [br][br]Per aiutarti disegna il grafico della tua funzione a(t) che calcola la x al variare del tempo. Come cambia il grafico se ad esempio il punto non si muove più con v=1 ma con v=2? E se v=4? Quindi per un v generico...

[b][color=#ff0000]UNA POSSIBILE VARIANTE[/color][/b]: il semaforo ha tre colori, lo sappiamo tutti. Crea un tuo semaforo che resta rosso 5 secondi, diventa giallo per 2 secondi poi verde per i successivi 8 secondi. Ovviamente ogni luce deve essere nella corretta posizione.