Wie wir gesehen haben, entspricht die positiv oder negativ [i]orientierte[/i] Länge x des blauen Schattens (in dm) dem Kosinus- und die des roten Schattens y dem Sinuswert des Drehwinkels. Für 0°[math]\le[/math]α[math]\le[/math]90° befindet sich P wie im Bild zu sehen in Quadrant I und beide Werte sind positiv.

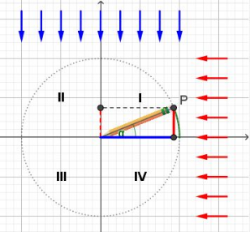
[u]Auftrag 1[/u]:[br]Erzeuge im folgenden Applet durch Klick auf die grüne Schaltfläche (0°[math]\le[/math]α[math]\le[/math]90°) einen zufälligen Winkel (in Quadrant I). Deine Aufgabe ist es, für[color=#ff0000] y=sin(α)[/color] und [color=#0000ff]x=cos(α)[/color] Schätzwerte einzutragen, die um höchstens 0.05 (dm) vom tatsächlichen Wert abweichen. Viel Erfolg![br][br][i]Tipp: Mit einem der beiden Schatten bleibt es übersichtlicher. Mit etwas mehr Sicherheit kannst du später dann auch Sinus- und Kosinus-Werte gleichzeitig schätzen. [/i]

[u]Auftrag 2[/u]:[br]Erweitere deine Untersuchung im nächsten Applet auf Quadrant II (90°[math]\le[/math]α[math]\le[/math]180°).[br][br][i]Tipp: Sinus- und Kosinus-Werte können auch negativ sein, achte daher genau auf die Vorzeichen![/i]

[u]Auftrag 3[/u]:[br]Nun kannst du den Vollkreis untersuchen. Erzeuge durch Klick auf die Schaltfläche 0°[math]\le[/math]α[math]\le[/math]360° zufällige Winkel und trage wieder deine Schätzwerte ein.[br][br][i]Tipps: Die Gitternetzlinien helfen dir beim Schätzen. Achte wieder auf die wechselnden Vorzeichen![/i]

[u]Auftrag 4[/u]:[br]Nun bist du fit für [i]Besondere Werte mit 0°[/i][i][math]\le[/math]α[math]\le[/math]360°[/i] ![br]Welche besonderen Drehwinkel werden hier zufällig ausgewählt?[br]Schätze wieder die zugehörigen Sinus- und Kosinus-Werte, die wir noch häufiger verwenden werden.[br][br][i]Tipp: Diese Werte kannst du dir auch in der Tabelle auf Entdeckerblatt 2 nochmals ansehen.[/i]