Honors Geometry
Resources for my 9th grade Honors Geometry Class
Table of Contents
- 3D Geometry
- Plane: Three points
- Plane: Point and Line
- Plane: Two Intersecting Lines
- Plane: Two Parallel Lines
- Extra Credit 1 - 3D Model
- Ratio & Proportion
- Exterior Angle Bisector Theorem
- Varignon's Theorem
- Classwork 54 #2
- Weeks & Adkins p.214 #13
- Projection of a Point onto a Line
- Trigonometry
- Unit Circle Trigonometry
- Unit Circle: Complementary Angles
- Law of Sines
- The Ambiguous Case of SSA
- Area
- Shoelace Formula
- Area of a Circle
- Constructions
- Constructing a Golden Triangle
- Surface Area & Volume
- Creating a Cone
- Frustum of a Cone
- Surface Area of a Sphere
- Cavalieri's Principle
- Volume of a Pyramid - Cavalieri's Principle
- Volume of a Regular Pyramid
- Archimedes Volume of a Sphere
- Homework/Classwork Problems
- p.519 #33
- Classwork 30 #2
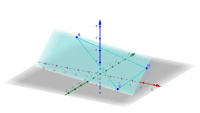
Plane: Three points
Three Non-Collinear points Determine a Plane
Exterior Angle Bisector Theorem
Theorem
An angle bisector of an exterior angle of a triangle divides the opposite side externally into segments proportional to the adjacent sides.
Setup for Proof
Given: [math]\overline{AD}[/math] bisects the exterior angle of [math]\triangle ABC[/math] at [math]A[/math].[br][br]Prove: [math]\frac{DB}{DC}=\frac{AB}{AC}[/math][br][br]Construction:[br]Construct [math]\overline{BE}[/math] parallel to [math]\overline{AD}[/math] through [math]B[/math], intersecting [math]\overline{AC}[/math] at [math]E[/math]
Explore
Move [math]A[/math] to change the type of triangle for [math]\triangle ABC[/math].
Will the angle bisector always intersect [math]\overleftrightarrow{BC}[/math]?
Unit Circle Trigonometry
Drag the slider for [math]\theta[/math] to adjust the angle. Notice the coordinates of point [math]P[/math] on the unit circle.
Unit Circle Definition of Trig Functions
We can extend the definitions of sine, cosine and tangent (and their reciprocals) to angles of [i]any[/i] measure, by using the unit circle.[br][br]On the unit circle, if the point [math]P[/math] has coordinates [math]\left(x,y\right)[/math], then from the right triangle we can see that, in Quadrant I:[br][math]x=\cos\theta[/math][br][math]y=\sin\theta[/math][br][math]\frac{y}{x}=\tan\theta[/math][br][br]Therefore, the point where the terminal side of [math]\theta[/math] intersects the the unit circle will have coordinates [math]P\left(\cos\theta,\sin\theta\right)[/math], assuming the angle is in standard position.[br][br]Since the signs of the coordinates depend on the quadrant, the signs of sine, cosine, and tangent will also depend on the quadrant.[br][br]We can determine the coordinates of the point on the unit circle by using [math]\theta'[/math], the [i]reference angle[/i] of [math]\theta[/math]. This is the acute angle formed between the terminal side of [math]\theta[/math] and the [math]x[/math]-axis. Completing the right triangle will get us the ratios for [math]\theta'[/math], which will be identical to the ratios for [math]\theta[/math], except that we may need to attach a negative sign depending on the quadrant.[br][br]You can drag the slider for the angle and see how the red reference angle changes and where the right triangle is that will allow us to find the coordinates of the point on the unit circle and, in turn, the ratios of [math]\theta[/math].
Shoelace Formula
Triangle Area (Counter-Clockwise)
What if we were to switch points [math]A[/math] and [math]C[/math]?[br]What would happen?
Triangle Area (Clockwise)
Shoelace for Quadrilateral
The formula can also be applied to Quadrilaterals or other polygons in general. Try dragging A,B,C,D around to see what happens if the quadrilateral is not convex, or if it is self-intersecting. Does it seem like the formula is still valid?
Constructing a Golden Triangle
Creating a Cone
Creating a Cone
A cone can be created by cutting out a sector of a circle and taping the two radii together.[br]In the diagram of the cone, we can see the Pythagorean relationship between the height [math]h[/math], radius of the base of the cone [math]r[/math], and slant height of the cone [math]l[/math]:[br][br][math]r^2+h^2=l^2[/math]
Central Angle and Radius
If we fix the slant height [math]l[/math] (which corresponds to the radius of the flat sector, what is the radius [math]r[/math], in terms of [math]l[/math]?
Relating the Angles
How does the central angle of the sector [math]\alpha[/math] relate to the angle between the altitude and slant height [math]\beta[/math]?
p.519 #33
This demonstrates the fact that, for a trapezoid [math]ABCD[/math], given a point [math]P[/math] in its interior, it is not necessarily true that:[br][math]A_{\triangle APD}+A_{\triangle BPC}=A_{\triangle APB}+A_{\triangle PCD}[/math][br][br]Drag point [math]P[/math] around and notice that the sum of the areas of the two triangles is not always half of the area of the entire trapezoid. Since all four triangles sum to the area of the trapezoid, this means that the two sums of areas of the triangles are equal if and only if each sum is half of the area of the trapezoid.