[math][/math]afirma que puedes demostrar que en todo [url=https://es.wikipedia.org/wiki/Tri%C3%A1ngulo_rect%C3%A1ngulo]triángulo rectángulo[/url], el area del cuadrado que formas con el lado mas largo ([url=https://es.wikipedia.org/wiki/Hipotenusa]hipotenusa[/url]) es igual la suma de las areas de los cuadrados de las respectivas longitudes de los [url=https://es.wikipedia.org/wiki/Cateto]catetos[/url]. Es la afirmacion mas viral en las matemáticas. [img]data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEAAkGBxISEhASEhIQFRUXFRcYFRUVEBYSFxcXGBUWFhYVFxUYHSggGRomHRcVIjEhJSkrLi4uGB8zODMtNygtLisBCgoKDg0OGhAQGi0lICUtLS0tLS0tLS0tLS0tLS0tLS4vLS0tLS0tLS8tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLf/AABEIAMUBAAMBEQACEQEDEQH/xAAbAAEAAQUBAAAAAAAAAAAAAAAAAwIEBQYHAf/EAE0QAAEDAgIFBQgOCAcAAwAAAAEAAgMEERIhBQYxQVETMmFx0QciQlKBk7HTFBYjM0NTVWJzkZKz0vAVNXSCocHE4SQlNFRysvEXY4P/xAAbAQEAAgMBAQAAAAAAAAAAAAAAAgQBAwYFB//EADgRAAIBAgMEBgoCAgIDAAAAAAABAgMRBBIxBSFBURMygZGh0QYUFSIzUmFxscE0UxbwI0KC4fH/2gAMAwEAAhEDEQA/AO4oAgCAIAgCAIAgCAICCtqmQxvlkc1jGNLnuOQa0C5JQHPNXu6vFLM5lVF7Hie8+x5ibtLb2aJvi3nbfZnbK2cI1It2TLNTCVqdNVJR3M6S03FwplY9QBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAcY7p+s/syY0URvTwuHLuBylmabiIcWMNieLsvBzrYitkVlqexsnAdPPpJdVeLNSewEEEAg7QRkV5qbW9HXyhGSytbjO6p65VGjrRkOnpB8Fe8kQ4wuO1vzD5CFfo4m+6RzGP2O43qUdOR2fQemoKyFs9PI2Rjt42g72uac2uHA5q4c+ZBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQGg91HW11MwUlO61TM3Nw2wxbHS9DjmG9NzuWupUUI3ZawmFliKihHtOR0zRGGstYDIHcf7/AJzXlzbk8x21CMaEVTta3iXCgWSJ+Ztu3/h7f7qWm80y995VotS50ZXT0kpqKSTk5DbG0i8coGxsrN++zhmLmxW6liHDc9Dz8fsqniFmhul+TsOpevUFf7kRyNSBd0Dje43vidskZ1ZjeAvRjJSV0cjWoToyyzVmbYpGoxVJp+OSolp2MnJjcWvk5I8kHBjX4cfGzh5UBlkAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAY3SWnqanfHFNKGvk5jbOJdYhpPeg2F3NFzxQGSQGD1w1jjoKd0z++dzYo75ySHmsHpJ3AErDaSuShBzkox1Zwh8skj5Jp3Y5pXYpHbr7mt4MaMgOAXl1qrnK53Gz8EsNTtxeoc2+1adC80mrMgkcW5DO/lI6ekfxU0lLeyvOUqfurf+iWMCwts/Oai733m6Cio7itYJlvPHiLbFzXNIc17XFr2EbCxwzDltpzlDeinisPDE/wDHJdvI6Jqf3Sywtg0kQBkGVYFmngJ2jmH547077L0KVaNT7nJ47ZtTDO+seZs9Fqu4VzawexGtD5X44YiyacSts2OZ2xzG869zchps2xvuPONvQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEBp+t2haiaeOSnY4SYGMbUNrJIuStMHvxwA4ZWlt8s7nIgDNAbTV1LIo3ySOaxjGlz3ONg1oFyT0WQHANZtOyaRqDUOxNibdtLGfBYdsjh479p4Cw3XVDEVrvKtDp9k7OcY9NPV6GPa/ccj/A9XYqjXFHvRnvtLUqe+wv8AnqWFvZKUlFXPI2nadp29iy3wRGEWt71Z45tsx9W49h6Vm/Mw4Wd4lJm3DncD6erpTLx4GHV4LXkSMbbt49Kw3cnCOVHrmggggEHaDmsJ2MyipKz0MxqprhUaOIYA6el2mAnv4hxgcd3zDlllbNX6OIuvfOYx+yMss1DtR2nQGnKesiE1PIHsOR3Oad7XtObXDgVcOfatuZkkAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAcZ7qGtHsuU0MLgaeJ3+IcDlLK03EI4sYbF3F1huzrYirkVlqevsrAesTzy6q8TUwvNOy0KXNB2or8CMopqzIGnME5t8E7SOk8eg8PrWxpWstStHNfNLfHh5lwCtZaTTW4PdYElEg5JK7IhHfM5HdxaOHb/AGClmtuRpVPN70tfweteRk7yHcewrFr6ElNxdp95VI+w4ncOJRK5KcsqEbLde89Kw3cQjl+71JaCrmppeXpZOSlyxZXZKB4ErPCHTtF8it9LEOG56Hm47ZdPEe9HdL8/c6/qVr9DXHkZByFUBnC51w8Da+F/ht6No3jevShNSV0cjXw9ShLJNWZuAUjSeoAgCAIAgCAIAgCAIAgCAIAgCAIAgCA0Pun63GmjFLTutUzN5wz5GLY6U/OOYb057lrqVFCN2WsJhZYiooR7TkUVMGNAZlYdd/8AlxPTtXlym5O8jtqeGjSgo091vH7kjJNxyPDs4hRaNsZ33Pcyl+Ztu39n5/msrcrkZPO8q04+RLZRNxGWkZt+rs4FZvfczU4OO+HcUsdiN9w3dPE/y+vgpNZSEJKq78F+SZQLBS+1jfZvuiIytZ30IWAjvsyNw3gfzWx2e4rwjKLzarxRO11xktbVixGSkro8e6w/P1IlcTkoq5C+mDgMV8QIcHNJa5rhm0scM2kbiFsjUcH7pWq4SnWhaort+H2Og6od0p0WGDSTrtyDKsC3UJ2jYfnjLjbavQpV4z3cTk8bs2phndb48/M6tFIHAOaQQRcEG4IOwgjaFvPNK0AQBAa/rtUVDafDTRzOc92F74sGOKOxL5Gh7gMVhhHAuBsbWIHnc+mc7RtAXte13seMHHziQwDEczttfPPPOyA2FAEAQBAEAQBAEAQBAEBhNb9Y49H0z55O+PNijB76SQ3wsb6TwAJ3LDdtSUYuTsjgzqiSZ8lRM8PmlOKRw2cAxo3MaMgOheXXqOcvodts3Bxw9L6vV/oqWk9Eim3DednR0+RZjzNNWz93j+PqeNOHI7PG/F2+hZfvGIXpK0tOfmTKJvIpHXy2cTwCklbeaakr+7f7njsNgbgcDcfV0hFm5GJOnZNNLkypkm45HdwPV09Cw1xRKNThI85x6AfrI7PT1LOhjrytwXiSqJuI3N3jI7+B6+1ZT4M1SjZ5o7vwUQvxG+zgDt6/L+d6lJW3EKcukld8OH7JwoFgiqZQ1pLsxsta5JOQaBvJ2WUoRcnZGjE1YUqTlPQ23UXQla01NNJW1lNyXIuEML2FsfLMMhZ7o11iMhYWF7rTtjatTAZFFJ3vqcNljVk5JWXI2v2v1PytpP7UHql4v+V1/wCuPiS9XXMifoOpDmD9K6Tzv4UG4fRLdD0mrypynkjutz43MdAr2uS+1+p+VtJ/ag9UtP8Aldf+uPiZ9XXMgrtC1TI3vGldJXAvm6D1S20PSevUqKLhHf8Acw8OktSc6v1PytpP7UHqlq/yqv8A1x8TPq65j2v1PytpP7UHqk/yuv8A1x8R6uuZDSaEqXNudK6S2uHOg3OLR8F0LbX9Jq9OVlCOifHirmFQT4k3tfqflbSf2oPVLV/ldf8Arj4mfV1zJ9SHzsrtIU8tVUVDI4qZzDMWEtMnLYrYGgeC3duXUbLxssXh1VkrO70K9SOV2N4XokAgCAIAgCAhq6lkTHySOaxjGlz3ONg1oFySeACA4FrNp9+kan2QbiFl20sZysw7ZXDx32B6BYdKoYmtf3V2nUbGwGVdPNb+HmYx7N42/wAD19qq34M9xwad46/k85UWN8iN2/otxTKOlSTvryKo27ztP5ssN8EZhF9Z6v8A2xWsGwgku3mi/BvZwHR+TNb9SvO9Pqb/AKEc9uTd3pk+bbMm+8bt3kWY3z8jVVyqi7RzfT6lhJTnA3vXl3fm3JNw43WNixwNm8D15repq73o82VBunGyd9+6267+nIyj8wG5XIF+gfnZ/ZVludz15XlFQevH6Ad7YbR/EdfEfx9KP3vuZinSVuH4JQVE3J33ojd3xtuG3p6O1SW5XNUvfeXgtfLzK3sv27wsJ2JygpIoElsnW6Du8vA/noWbX0I9Jl6/ebv3LNVvZMja+dvuMbv8K0+G8ZGoI4DMN6bngvRw9HJG71OQ2pj3iKmWPVXj9TZdH/rPTHXSfcOXKeletLt/RUw+jM6uPLJbzc+P970K1S+BU+8f2ReqLhVSRaaW95l/4lWcJ8aJiWhdlV3qZCwC10bzP3n/AHj1axnxOyP4RGOhdKqSMPqt+tdKfs9F/UL6N6OfwY/dlKt1zdl7ppCAIAgCAIDm3dnZVuhiEbHOowcVVyd3PyN2BzBnyQOZtfYL2AzhUzZXl1LGFdJVU6vVOZxSBwBaQQdhGYXjtNPed9TnCcU4Pd9CsoTIcGI3Owc38X5/mp3y7ivkVV5npw8z3HbJ3kO7y8Co2voTUnHdLvJHOsLlYtc2OSSuyhg3nb6Bw/P8llvgjXCLvmlr+D17N4yP528UTMyhd3W5lBltkRnuHHqP5smW+hF1bbnr+SuNtuvejdycI5Vv1K1gmQSgjm2ud27pPQfz1TTv1itUTi/+PV8CuEi1hu3Hb5e1Rlc203G1kSLBsL/VfV52kankBcQMs6qeDbvTzYWnx37+DbngruFo/wDdnO7Zx9l0EH9/I79TQNjY1jGtaxrQ1rWiwa0CwAG4AK8cwaHSueNJ6XwNYc6W+J5b8Adlmlcj6Tqm3TztrXRFmhffYzOObxIfPP8AVrlMuG+aXcvMse8QSvmxx95F4XwruH0as044foJ2lLWPBfX6mHe6Jsc3iQ+ef6tVsuG+aXcvMz7xa6UfNyMt2Rc0/Cu9WrGFjh+mjaUu5eZiV7F2XzeJD55/q1occN80u5eZneMc3iQ+ef6tYy4b5pdy8x7xbaPfNgHeRc5/wrvjHf8A1qzio4fPvlLRcFyX1MRvYuOUm8SHzz/Vqtlw3zS7l5mfeMfqgXfpTSmINB5Ciya4uHw+8gehd/sBRWDWTS71KdbrG8r2jUEAQBAEAQHlkBzXXTua4i+o0cGxyk3kpycMUp3lnxUh+yd9sytVWjGot5dwePq4aXuvdyOYucS98T2vjew2ljeML2nxSOnjsI61586bpvedZh8ZDFpZH91x+xOFpPQPHBDDVyDpGbRu334jiBw/stl91uJVSd7rfFEzHAjJa7NFqMlJXR64oG7K5GG4syOocOnoKlfLuRpUM/vS7PoMRbt2ceHX2+hLX0M5nDdLTn5lb32F/wAlYSNkpJK55G3edp29nUjZGEbb3qw9l+g7iidjMoZt/EQQyzSR08LcU0pwsHg/Okdwa0Zn+a3UaOd/Q87H494anZ9Z6eZ3zVPV6KgpmU8edu+keedJI7nyO6T/AAAA3L00rbji5Scm29TMrJg0PR/6z0x10n3DlxnpXrS7f0WsPxM6uPLJBNz4/wB70K3S+BU+8f2YeqJ1UMlppb3mX/iVZwnxomJaF4VXepk8WAW2jeZ+8/7xytYz4nZH8IjHQuVVJGJ1W/Wulf2ei/qF9G9HP4MfuyjW65uq901BAEAQBAEAQBAa3rhqbT6QaMd45mj3OdgAez5p8dnFpy6jmsSipKzJ06s6cs0HZnGdN6KqKGQRVbQLm0czfepeo+C/5hz4XC8+thnHfHQ6vAbXjWtCrul4MspDc4R5TwHDrVZbt5603meVdpIAsGxKysihzN4yP8D19qzfma5Q35o6lDX4jbZbaOJHpA9KlbKrkFPpJZXw8SdQLAKGH9S3a3whs3N/mOB6PRcrY2tGVYwd88dOC/ZMx4Oz/wA61rasWYyUtCmomDGlxvYcMyTuAG8lSjFydka69aNGDnLRHXO5lqiaSM1NQ3/FTNGIHPkY9rYR07C7ieoL1qcFCNkcLisTLEVHOXYb0plYIDn1NUBmk9L3DznS82N7/gDtwg2XI+k9JzdO1uOrsWcO7XMv7Pb4s3mJfwrlPVJ813rzLOZEMtc3HH3svhfAS8P+Ks08LPoJq6/68V9SLlvRN7Pb4s3mJfwqt6pPmu9EsyNc1g09K2ZsXJ2gdDMb8nJyj3Maw5NLQGtGLpv0Db7WA2dSdPO3eakuKsk+3eapzdxqlrPJUXMwcMUbJWMbSSNIY9zhcPDnCRmQFyGm4OViFHaey6dJLouDs25L/wBWYp1G9TY/Z7fFm8xL+FeP6pPmu9eZtzIttH1zcHNl5z/gJfjHfNVnFYaTqarRcVyRGMlYufZ7fFm8xL+FVvVJ813rzJZkYbQulI4a7TVQ/GGR0tI9143B1mioJs0i5K7/AGBBwwaT5spVusZbue6wyVjawyyQvcyoIa2JzXNjjdHG5jMQ59iXjEdpDt1gvaNRtqAIAgCAIAgCAIC10no6KojfDPGySNws5jhcHsPSMwgONa3ahz0GKWnD6iluSRzpoB075Yxx2gbb2uqtbDqW+Op7ez9rOj7lXeufE1mKUOAc0gg7CM157i07M6unUhUjmg7o8kcdg2+gcez+yLmyM237q/8Ah6YxYDhs6EzO5l042sUh9ud9e7y8Fm19DCk47pd4d3xtu39nb/dFu3hvO8q04ktlE2lD2b9h49vQsp8DXOK6ydn/ALqbl3LNVzVSNr52jkY3f4Zp2SSAkGcjxW7G9NzuF/SoUcivxOP2nj3iJ5F1V4/U3LQmiqhlbLJLDI4mSZ3sr2WRGYXkcjEKcONy0ACxaALFwJJKsHlG4oDVvbcGVVTBNG8MjnghZK1hcwGaOMs5R24l78IsDuva6AxlB+s9MddJ9wVxnpXrS7f0WsNxM7ZceWS3m58f73oVul8Cp/4/sw9UXFlUMmO01SMcwyFt3sY8Mdc5B4Ad9eEfUr+BxE4TVNPc2r9mhCSWpVo/Q0EDnuijDC7Im7jkCSGtuThaC5xwiwuTkoYnHVsQlGo7pf72szGCWhf2VMkWujh3n70n3j1axnxOyP4RGOhdWVUkYjVYf5rpX9nov6hfRvRz+DH7so1uubfTUccZkLGNaZH43kC2J+ENxHibNaPIvdNROgCAIAgCAIAgCAIAgOc669zcSF9RQYIpibvhPewzHecve5D4wyO8Z3WqpSjNby5hMdVw0rxe7lwOXMxNe+ORj45mH3SN4wuaere3gRkQvPq05Qe/Q63AYyliI3i/e4olWk9AjkduG0+jeSsrmaqj/wCq1ZS1uECwuOG/ycer/wAWW8xGMHS6u9ciRrwRcKL3G2MlJXRkdWtX36RqRTtuIWWdVSDKzDsiafHfa3QLnoVzDUb++zwNs7QyroKb38fI77SUzI2Mjja1rGNDWtaLBrWiwaBuACvnLkyAIDAVOqVO+d87jNd8sUr4+VIje+ENERcz5pY09JGd7AIDB6PH+Z6Y66T7grjvSqLbp2XMtYfiZ3CeBXIdHPkyzdEEzTykeR8L0K1ShLoKm56x/ZFtXRPhPAqr0c+T7iV0WmlmnkZcjzSrGEpy6aO4jJqxeFp4H6lodOV9GZujzCeBWOjnyfcZui20a04Nh50n3jlaxdOXSaPRfhEYtWLnCeB+pVejnyZK6MRqsP8ANdK/s9F/UL6J6OprBRvzZRrdY3Ve4aggCAIAgCAIAgCAIAgCA17W7VCn0gwCUFkrfep2ZSRnhfwm8WnI9BzWGlJWZOnUlTkpRdmcX1g0RU6PfydU0YSbRzsB5KXgPmP+afISFQq4ZrfHQ6nA7YjUWWrul+SzjbvO07exVW+CPZpxtverK1g2FDKaSWWOGnbimldhYN3S9/zWjMn/AMW+hTdR2eh5e0sVHDQzLrM73qlq7FQUzII8zzpJCO+kkPOkd15AcAANy9NKyscZKTk3J6szSyRCAIAgOfU9LG/Sel8ccb7GltiYHW9wOy4XIelFWcHTyu2paw6vcy/6Lg+Ig80zsXJ+t1/nfeWMqIJdGQY4/cYfC+CZw6lZp4mt0FR5n/1/ZFpXRP8AouD4iDzTOxVvWq3zvvJZUWulNGQCGUiGHmn4JvYrGFxVZ1opyfeYklYuzouD4iDzTOxV3iq1+u+8zlR5+i4PiIPNM7E9ar/O+8ZUW2j9GQFnvMPOf8E34x3QrOLxNZVN0nouP0RGMVYuf0XB8RB5pnYq3rdf533ksqLDU+FrNKaUaxrWjkKLJrQ0fD7gvoHo/OU8EnJ3d2Uq3WN5XtmoIAgCAIAgCAIAgCAIAgCAttIUEU8b4po2SRuFnMcMQI6kBx3W7UCaivLSiSemGbmc+aEdG+WMfaHTtVWthlLfHU9rAbXnRtCrvj4o1A1jMHKBwLbbRnfoHTusqPRyzZeJ00sXSVJ1b7jr/cx1RNLGaqobaqmGY28jFtbEPnbC7py3L1acFCNkcRi8VPEVHOXYb0plYw+t0E0lM9kEYkeXR3YXll2CRpfY42AnCDZpcAdhyQEGpFBNBS8nOHBwlmLQ54eRG6V7oxdpIFmkC261kBn0ByHWjTxp3aRqJ6nSmBlcKeOOmnZG1rTTxy3ONpttd1kgIDKapRYKzSg5SeQH2I4OncHSWdTlwDiAMxey430r1pdv6LWH4m2XXHFogm58f73oVql8Cp94/sg9UT3VUmWmlveZf+JVnCfGj9yMtC8JVd6mUjy6wZLbR3M/ef8AePVrGfE7I/hEYaFzdVSRidVv1rpX9nov6hfRvRz+DH7soVuubqvdNQQHhNtqA1ah1+oZpGRRvkHKFzYpXwSMhlcwHEGSkBrrWO/cgIO5/rI+tNVeop544zGGOjaI3FxxiQmPG4tiJADC6zjZxzFigLiv17poZJInRV5cxxaSyhme0kG3euDbEdIQGc/SkYg9kuJZHyfKEvaWlrMOLvm7QbbtqA16LXummbM2N8kEgp3zsdVUssTDG0e/C9sbASDkQTuQE+oOnXVkEkxlilbypbE5ga1/J4WEcqxrnBjyS44doaW3AN0Am14pG1baYzU+EwvkM3siMMaWvDeSdnk7O+3cUBV3RdNS0ej6ipgwcozBhxjE3vpGtNxcbiUBbx68U0rZ2MlMMrIHStdU08sTCwD35odhMkYPAglATagaddWwSTGWKRvLObG5ga13JhrC3lWNc4MeSXHDtDSy4BugNnQBAcX7qWgooK+ilphyD5BNK8sa0tMsRiwScm4FmPv3Z222O3NWMLQVaplZWxmLnh6Lkt+/Qs/bBpP5SqPM0/q16fsqHzM8X23P5EUyaxaTA/WNRtHwNPvIHxajLZcEr5mThtmcnbKir2waT+UqjzNP6tS9lQ+ZkPbc/kQ9sGk/lKo8zT+rT2VD5mPbc/kRRFrFpMgH9JVGY+Jp/VrEdlxavmZKe2pxk1lRbU9ZWsMzm104Mr+Uk9ygOJ+FrcRBjsDZrRlwWfZUPmZH25P5EZzULRVTWzaRkdpGqY8PhDnMjgvJ7kcJcDGQLDLKy8HaOzcPOplqxzW0ue7g8TKrSVTS5uXtLqPlau83TeqXn+xsD/UvHzLXSz5lJ1IqCQf0tXXGz3Om3/8A5qS2Tg0nFU1Z/cx0kuZV7S6j5WrvN03qlH2Ngf614+ZnpZ8ymXUedwLTpauIORHJ03q1KOyMHF3VNeI6SXMq9pdR8rV3m6b1Sj7GwP8AWvHzHSz5j2l1HytXebpvVJ7GwP8AWvHzHSz5lMepE7RYaWrgMz73TbySfg+JKlLZODk7umvEx0kuZV7S6j5WrvN03qlH2Ngf614+ZnpZ8y/1Z1WNJLUTOqZ6h8zY2udK2NthFjw2wNA8Mq7QoU6EMlNWRBtvezY1uMBAQ1kAkjkjJIDmuaSNoxAi4+tAaPqjozSlM2jo3xUbaeAuD6jlDI6WPPCGRWBjcbi5JKA3xsYGwAdQsgNYr9R4pZJJTVaTaXuLi2OvlYwXN7NaMgOhAZHS1BOKKWCklLZhCWQySOLjiDbNc5xBu753E3QGn6r6r1cdfTVU0AY0U0kUpfXPq5HSOLXY3F+xpIIDW7Oi9gB0ZrANgA6hZAajUdzyifWNqTT0vJiJ7HQGlYWvkc8O5YnZiABGy+ZzQF13RtCy1uj6imgDTI/AG4nYRlIxxz6gUBjtH6GrZtIU9VVxQRMpoJImCOUy8s6Swc/NowssMgc0BurGAbAB1CyAqQBAcr7r/wDrNG/RVXpp1f2b8fsZ5m1/4z+6NTXRHJkc+zyt/wCwUKnV7jbR63Y/wSLYamFgIjp+a3qUKfVRsrddki2Go3TuOc/Sn0kH3RXM4/48jsdmfxonTFTL4QBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAcq7sBPsvRtre9VW023wdCvbOv027kzzdqpPD73xRqN3cG/bP4V7958vE5jLT+bwI5y62xu1vhnxh81Qm5205cTZSjTzdbg+H0JLu4N+2fwrZefLxNeWn83gAXeK37Z/CsXny8Rlp/N4EVOXYW5N2eOfwqNOU8q3eJsqxp5373gS3dwb9s/hU7z5eJqy0/m8Ddu41fHpS/xkG+/wAEVzmOv08rnWbNt6tGx01VC8EAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQHK+69/rNG/RVXpp1f2b8fsZ5e1/4z+6NTXRHKEc+zyt/7BQqdXuNtHrdj/BHXzOYwloF7tFyC4NBcAXEDMgAk+RQrzlCF4mzC0o1KlpaFOjKkyMxG1w5zSQCAcLiLgHMX22WMPVdSF2ZxdFUqmWOlkyan5repbKfVRprddkimaza+5fIGt0y4yiEAxEynDaO0B90OLLLbnlkuax/x5HX7M/jRNs1FrpH+zopZZJTDUBrXPMbzyboYns90jaGvviLtl24sOdgVTPQNpQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAcq7sDrVejfoqrcTvg4K9s52rdjPN2rFyw7S5o1Dlh0/Zd2LoOkRy/QS/1lE8wtv2t8F3jDoUKlRW7jZSoyUux/gTFrgWnFboDwcjcEEZhJuM1ZinGpCWZW8BBgYA1oIA+a47TckkjM33pBwhGyFSNSpLNLU8p5hhbt2eK7sSnUWVCrRk5vzJOWHT9l3Yp9IjX0Ev9Zu3ccs52lARcGSEEEbRyJyIK5zHO9ds6zZqaw0UzotBQRQNwQxxxsuThjYGNudps0WuqheLlAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEByvuvf6zRv0VV6adX9nfH7GeXtf+M/ujU10RyhHPs8rf8AsFCp1e420et2P8EimamECI6bmt6lCn1UbK3XZIpms3TuOc/Sn0kH3RXNY/48jsNmfxonTFTL4QBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAcr7r/APrNG/RVXpgV/Z3xuxnmbWTeHduaNSuuhzLmcrklyI5zl5W/9goVJK3cbaMJZtOD/BJdTzI1ZJcj0FMyChLkRU571vUoU5LKt5srQlne4kup5lzNeSXI3XuNnv8ASn0kH3RXN49/88jrtmK2GidMVMvhAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEBidOatUlYWGqgjlLL4Md+9xWxWsd9h9SXsDGf8Ax1or/YwfU7tWcz5mLI8Pc50V/sYPqd2pmfMWRj9O6k6NghdIzRtM8jbjk5FjW5l0kkjicLABckAnoTM+YsirQWpmiamngqBo6JglYHhrr3FxfaDn1pmfMWRfDuc6K/2MH1O7UzPmLI9/+OtFf7GD6ndqZnzFkZXQer1LRh4pYWRB5BeG3zIuATc9JWDJlEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAEAQBAWOl6F0zA1k0kLg4OD2YTs8FzXAhzSDmCgKdBaKbSwRwMc5wYD3zrYnFzi5xNgALknIAAIDIIAgCAIAgCAIAgCAIAgCAIAgP//Z[/img][br][br][br]Si en un triángulo rectángulo hay [url=https://es.wikipedia.org/wiki/Cateto]catetos[/url] de longitud [img]https://wikimedia.org/api/rest_v1/media/math/render/svg/1d73aa5354c24942dab5316be466465a9d171510[/img] [img]https://wikimedia.org/api/rest_v1/media/math/render/svg/4b1bcf19f4ec75b1d2cc0be001e58a314fb0a940[/img], y la medida de la [url=https://es.wikipedia.org/wiki/Hipotenusa]hipotenusa[/url] es [img]https://wikimedia.org/api/rest_v1/media/math/render/svg/8573e7d95140b0d4068258d8162e189563baee6b[/img], entonces se cumple la siguiente relación: [img]https://wikimedia.org/api/rest_v1/media/math/render/svg/b4e89a8fb02916280c36043b2937ade5d8315304[/img][br]De esta [url=https://es.wikipedia.org/wiki/Ecuaci%C3%B3n]ecuación[/url] se deducen tres [url=https://es.wikipedia.org/wiki/Corolario]corolarios[/url] de verificación algebraica y aplicación práctica:[br][br][table][tr][td] [img]https://wikimedia.org/api/rest_v1/media/math/render/svg/ca09e8ee119ce95c893ceb2ac1f7ccd3a40fad9c[/img][/td][td] [img]https://wikimedia.org/api/rest_v1/media/math/render/svg/3fabe577a6a4ec15f7428e9ee9711da32d79bc00[/img] [/td][td][math]C=\sqrt[2]{a^2+b^2}[/math][br][/td][/tr][/table][br] [img]https://upload.wikimedia.org/wikipedia/commons/thumb/f/f2/Pythagorean_right_angle.svg/180px-Pythagorean_right_angle.svg.png[/img][br][br]HISTORIA[br][br]El teorema de Pitágoras fue comprobado en el siglo VI a.C. por el [url=https://es.wikipedia.org/wiki/Filosof%C3%ADa]filósofo[/url] y matemático [url=https://es.wikipedia.org/wiki/Antigua_Grecia]griego[/url] [url=https://es.wikipedia.org/wiki/Pit%C3%A1goras]Pitágoras[/url], pero se estima que pudo haber sido previo a su existencia, o demostrado bajo otra denominación.[br][br]El teorema de Pitágoras tiene este nombre porque su demostración, sobre todo, es esfuerzo de la [url=https://es.wikipedia.org/wiki/Escuela_pitag%C3%B3rica]escuela pitagórica[/url]. Anteriormente, en [url=https://es.wikipedia.org/wiki/Mesopotamia]Mesopotamia[/url] y el [url=https://es.wikipedia.org/wiki/Antiguo_Egipto]Antiguo Egipto[/url] se conocían [url=https://es.wikipedia.org/wiki/Terna_pitag%C3%B3rica]ternas de valores[/url] que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y [url=https://es.wikipedia.org/wiki/Papiro]papiros[/url]. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación.[br][br]
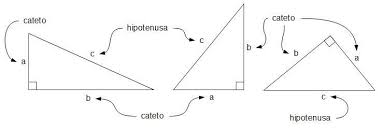
[img]data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEAAkGBxMSEhUSEhISEBUVGBIXEhcVEBUWEBUYFRUXFxcVFRcYHSggGBolGxUVITEhJSkrMi4uFx8/ODMtNygtLisBCgoKDQ0NFQ0NDjcZFRkrKzcrNystNysrLSstKy0rNysrKysrKysrKysrKysrKystKystKysrKysrKysrKysrK//AABEIAIQBfgMBIgACEQEDEQH/xAAbAAEBAAMBAQEAAAAAAAAAAAAABAEDBQIGB//EAEIQAAIBAgMDBwgJBAEEAwAAAAECAAMRBBIhMUFRBRMiMlJhcRQVM0KBkZTSBiNUYnOCkrLTU3KhsfGiwcLwJDRD/8QAFQEBAQAAAAAAAAAAAAAAAAAAAAH/xAAUEQEAAAAAAAAAAAAAAAAAAAAA/9oADAMBAAIRAxEAPwD9xiIgIiICIiAiIgIiICIiAiIgIiICIiAiIgIiICIiAiIgIiICYJmZBinNRjSUkAelYGxAOopg7mIOp3A7iQYDB47PVdQOgFUq1+sSzq1hbqjKNd+u4Am+RUVArEAAAU6YAAsAAz2AEtgIiYJgZiec3dPNOsGvlINiQbHYRoR4wNkTXRrK6hlIZWAKkagg7CDwmyAiIgIiICIiAiIgIiICSYjHhTlCtUfblQC4HFiSAo8SL2Nrz1yjiCiFhq2gQbizEKoPdciZweGyLa+Y7WY9ZmO1j4/40GwQMJVYqSUyHWy5wd3ET5yryzXCUiLuzBWqjyd1CnNRD0950FSobWvpqeib/V2mbQPjDjsXkZAzXyvlYoecY3rXIsvWXKlhs016wnUweOrGsqEFluq6oRen5OH58txNUlLf40netFoATMRAREQEREBERATBMhrY5iStFOcIuGYvkogjapaxJO7RSAQQSDPOLWq1CoGVQ5SoFVHLjVTaxKrrfugXh5m8+OxdTE0mphnrZBUVOcFKk1Uqy4U2HQ7RrjQX6J2kCY5QOOei6fXZmpuAFWnbL5PV6TNbo1uc5sWU7SthbMQH2YifL16mMLuFZ1XMoWyL6MtSGYZksGtnuCTtbojSKeIxgqZCKtuiFbm0K2WrigzNa2uQYU7r5hb1rB9RE+RbFY0BLCs1nS7ZVIdc9HOchpKVGXndCRsNi/Rn1FbPboBWPBnKj3hT/qBuic7yyqmtakFXW7U6vOKoG9wyq1vANOgrXgZiIgIiT4zEZALDMxNkXezcO4bSTuAMDXjMQbinT67b7aIvbb/QG89wJG7C4cIuUbO/UknUsTvJJJJ754weGyAljmdrF2ta54AblGwD/ZJJpgSJ6dvw6f76krkienb8On++pK4His4VSSbAAknuG2S8nB2UVHY3cK2Swy07i+UWFyeJJOuyw0meWFJoVgNpp1bfoMposCoI2EC3haB8vj/ozUek1IcwC3OZqlvrKmYVMrvdDZlz7jfbZlnofRluczHm7Z2cgWBBaqKhcE0ycx6psRcIuu4fUyN6h59Vubc3UJG6+amAf3QONgfo49PmdaQ5tcOt1vmTmSxYU9NlQGzbNp2zvYiizCwqNT71CE/9akTfEDn+QVPtVb9GH/ino4WsNle/99FT+wrLogQEYhf6FX9dL54GPZfSUai/eW1RPZk6XvUS+IGnD4pKgujBxsNiDY8DwPdN0lxWBVzm1R9gdTlqDuv6w7jcd010MSynJVsb6I4Fg3cR6rd2w7uAC6IiAiIgQcoa1KC/fZj+Wm9v8lT7JfIMfpVoHi7r76Tn/wAZfATn42mzVaah3p9Cq11O9WpAXBBDaM2hB2zoSOp6en+HX/fRgazWq0+uvOr2qY6Q7zTJufyknulOGxaVBdGDW0PEHgw2qe4zdaT4rAo5zFbMNA6krUA4Bl1t3bIFMTnkV6e8YhfypX9h0Rz+i3EzdhsejnLcq41KMCtQd+U7R3i474FUTAMzAREQEk5VrFKTFTZjZUO7O5CJf8zCVyDlI5mopxqZm7lpguD+sUx7YFWGw4RQi7FAA3mw4nee+bCJmIGMo4RaZiBi0ZRMxAxaZiIGGnBq8t4fAUguKqrQVWFOkzaIUJPN2PctlN9mW50IJ78i5U5JoYlBTxFKnXQENlqKGTMLgGx0O0wKMPiEqKHRldWF1ZWBUjiCNDNeDx1OqM1Nsw0scrAEEXDKSOkp3EXBmcHgaVFObo0qdFNbLTRUTXbooAmjk/BCggQVHZVChM+ToKosACqi4AG1rnvgVYiuqKWY2A9vcABvN7ADfeT4SixPOPo5FgL35tez4mwJPG24Ca8ODWYVD1F9EO1celb/AMRwNzqRl6AEDMRECRPTt+HT/fUlc5PKWL5o1qts3N0A9r2zZTUa17G17cDK8FjlqA2DKVIV1YWZSVVgO/osp048YFTC8h5HP1eX+m9RB/ajkIPYuUeycUfT3BvixgaNQ4iuQ5IpDNTBTahe9g23uFjcid/k7DlEAYgsSzNbZmdizW7rtYdwECqQYQ5q9ZuzzdIDwXnSw8eeUfklxkPJOxzvNWtm9jkD/pCwL4iICIkmLxeUhVGdzsUG2+2Zj6q9/uBOkD3i8WtMXY7TZQBd2a1wqqNSdDp3GS4THvnCVk5svc0rNmBsLlGO5wNbDQjYTYzzV5Pe4rXD1lva+lPKbFqQGuVTlXpam4Um4GWeatNsQMuVqSAqbsuWtmU3GQEdGxHW3200s0DrTTicOHUqRoe+x7iCNQQbEHcRNOCxJN0qddbXsLK4Ox14A8NxuNdCbIEfJtZmBVzd6bFH7yACrcOkpVrDZmI3SyfLVvpElPlVcFzVc1K9EOHCpzAFM1DmJzXvtU6bQu6fUCBmIiBFyshNO6i7IVdQNpKEEqPEAr+aVUqoYBlNwQCCNhBFwZ6InyfKtTlHD4qn5JhkxODsTWU1aaVgzvrzRYgWUC4U6HORcaZQ+tkdT09P8Ov++jPHKuNNKmHAAJZFAbcWIGutr+0DvEl5Kx3P+TVrBecoVGsCCAWNAkXG2xgdmIiAImnE4VKgs6ht4uNh4g7j3ibogQeT1afo35xexVJv+WoLkfmDeInqjyitwtQNScmwDgAMeCsOix7gb9wls8VKSsCrAMDoQRcEcCDtgeiZzxj2Nc0ugAvN5iz2c5w5GRba9Tjx4a5PJ7J6Fyg7DXej7ATmTQWAUgDgZ4bFhSDXpc0RsqaPSF9v1gAKD+4KPGBL9K+V8Rh6ebC4OrjahByqhVUXvck39ignwm/kI1KtNMRXTmqr00vTsfqswDOhvrmzWv8A2jhc9MMCAQQQdh3GegIGYiICIiAiIgIiICIiBgyCp9cxT/8ANTZzudh6g+6PW79O1PWLrF25qmbEgGow9RTw++d3DU7gGqoUgihVAUAWAGwAQPYEzEQEREDm4rDLVerTYXV6KqwBIJDGoDqNRoZTgsEtIELfpG7FmLMTYLck6nRQPYJ5T07fh0/31JXA1nDoSGyqSNhyi4vwO6bBEQE+U5epcpU8VTqYFKNXDm5xVOpUyu7EKoNM5TlIVFtra5Nxvn1cQOVy9i3p4Y1FIpMDRuWsQoaqgbNY2tYm9j7Zv5Hxhq0s7ZetVUFb5GCVGVXW+5goO07dpGssYyAVGrdQlKe9x1nHCnwX7/6doaBsr4pmYpSsSNHY9RL7j2nt6vvtcX24TChAdpJN2Ym7seLH/tsG6e6FBUAVQFA2AbJtgJgCZiBLjcKWsVsrrcod2u1W4qdhHgdoBHrB4jOL7CDZlO1WG0H/ABY7wQd8okWMolTztMXYCzrf0ijcN2cXJF+8aA3AYq4Cm1ZMQVvUppVRDwWqULD3018NeJlwnz+K5NavXpYhHQovNMNLN0TUDa5b6ipaxNhlItc3H0EBERAREQMMoOhF5G6/X0/w6/76MtkdT09P8Ov++jAsiYvMwEREBERATBEzECGpyaAc1Imidpy25sn7yHQ+Ise+eTi6lP0qXHbpAsPFqerL7M3jOhMEQNdDEI65kZXXXVSCNNouJtkeJ5PRjnF0ftocrm2zNucDgwI7p4z1k2qK68VstUeKk5W8QR3LAviT4XGJUvlbUdZSCrr/AHK1iPaJvvAzERAREQElxmIK2VLM73yA7BbazfdFx7wN82YvEBFubk7FA6zMdir3n/nSasFhyLu9jUa2YjqgDYi39UXPC5JNheB7wmGCLbab3Zj1mY7WP/ugAGwSiIgIiICImLwJU9O34dP99SVyRPTt+HT/AH1JXAREQE1YiuqKWYhQLXPibe062t3zxisUEA2sx0VRqzHuH/c6DfNNDDMWD1bM2uUD0dO+nRvta2mY67bWBIgeRRatrUGWnuQ7W76nd9z332C8CAJmAiIgIiICIiBz6t6LFx6NjeoNyH+oOAPre/tE3gwy3kFH6lgh9G2lI9k/0j3dn3cLh0IgRAREQE5+Lp5q1MZmX6uubqbHrUdJ0JPXwauQxzAgMAVqMps1rjokX6o90CdFKV1XO7BqdUkMQdVakAdn3m986EhPJVPMGvVuAQD5RW2NYkdb7q+6e/N69qt8RV+aBXEk83r2q3xFX5o83r2q3xFX5oFcSTzevarfEVfmjzevarfEVfmgVxOfXwtNBdnqqNNTiattTYetxImwcnr2q3xFX5oFkSPzenaq/EVfmmfN69qt8RV+aBXEk83r2q3xFX5o83r2q3xFX5oHvEYNKlsy3I6puQ6/2sNV9hk4p1qfVIrr2XstUeDgWbwIHe02+b17Vb4ir80eb17Vb4ir80DGH5QRmyG9Nz6jjK5tty7nA4qSO+WXkFfkek4KvzjqdoatUK+4tKMHhFpIqKXIXQZ6r1H9r1CWb2mBvnitVCgsxACgkknQAakme5PjMGtUANmsCrDK7LquoPRIvrY+wcIGnCoXbnXBG0U1PqKd5HbO/gNON7RJPNy9qt8RV+aZ83r2q3xFX5oFcSM4BNuer8RV+aPN6dqr8RV+aBZE54w9IsU5184FyvlVTOBpqRnvbUe+bfN69qt8RV+aBXIa6lqqqHdBkYnKQLnMoF9O8++e/N69qt8RV+aePNSXzZq17EX8oq7Cb263cIHjCUctd+kz/V0+sQbdOpssJ0ZNhsEqMWBclgAS1R30BJFsxNusZTASPEYs5ubpgO+hPZQH1nO7fYbT4AkVOtxa5HeLXHvkGH5LKCy4isN50okk7yxNO5PeYFGFwgW7El3brMdp7gPVXgP9m5lMj8jf7TW/TQ/jjyN/tNb9ND+OBZEj8jf7TW/TQ/jjyN/tNb9ND+OBZEj8jf7TW/TQ/jmPI3+0Vv00P44FsTlrq5pjF1C42rahcaA6/VbbMptwImytRKAs2KqIBtLeTgDxJpwOhEiGEc7MTWP5aH8cz5G/2mt+mh/HAsmrEUg6lWFwdo/42eM0eRv9prfpofxx5G/2mt+mh/HAxg6zA81UN2AurEW5xRpm4ZhcBgOIOgIEtkDcmklS1eq2Vgw0ojUd4pg6gkGx1BPGXiAiIgIiICIiAiIgIiIHP5dwjVqL01Cktl0ckIbOGIYgEgEAjZM8k4RqdMqbKS1RgEJKIGYkKpIGgvwHhaXxA+TwXIGOTGNXflJ69E03VKT0EUIzMhBtTyq4ADC+h136zuc9Wp9dVqrvakrK47+bJNx4MTwUzoRA8UqgYBlIIIBBBuCDsIM9znUDzVQp6lQlqfAOdXT2m7jiS/ATowEREBERAREQEnxmJyAaZmYhUW9ixNzt3AAEk7gDN5kFA85WL+rTBROBYkGoe8DKq+IeBNylyKcTQq0a1ZwKtOpTIp2RFFRCtxvYgN6xINtm6a/ov9FqGApc3RNZhpc1a71CbcFJyr+UCd2IHFp8jkYryjnL9eyZDoHWmp1zW20gb5db2N7AjtREBERAREQEREBERAREQERECLD4DJUdg5y1Gzsth1sqJt22sg04k67AOV9LPoVg+UVAxNMlh1XRytRfAjQ7d4M+iiBzfIGpgczUawHUqMXpmw2XPTX2Gw4GVYPE5wdCpU2dTtVrXt36EEHeCJRIKX/2Htvp0y3DrvlPj1vcIF8REBERAREQEREBERAREQEREBERAREQNdeiHBVgCDtB2SM4Oqvo62nCqnOWHAMGVvaxadCIECtiBtWi/g7p/jK3+5jlZ6gRCmYdNOdNNc7hNb5AQb62B0va9tZ0IgfH4tsUz5f/AJAp9Ek5Vz9CrhyDdUGpTniVGbfs0WZpDGM1Jnz3V7sLWphjRxINyFF6WY0R61tDmve318SDkchvVIbnc5Fktziqr5sg5wWUAZQ2w+NiRaVVWrEnKtIDcWdybd6hR/uWxKOeMFUf0lbTs0kNMHuZizN+krLqVMKAoAAGgAFgANgA3T1EBERAREQEREBERAREQERED5vlDlupSeuCgZELimQ4DgrhRXIIKkW0bpXO0aTOF+kbtkXmkDVMhT68lAH54/WNzd1NqDaWOptfQzu1MMrbVU3ve6g3uMuvs08Jow/JVJKfNLTTJpdSoINtha/WOg1Mg4ND6UuVzcznzF2pgM+iLRpVLEqjdImp3C19RbWzD/SJmazUlUGoyIRWuSFxLUCWGQZT0QbAnba+mvXfBUztRDcgm6KbkCwJ02gaXh8GhBBVSDtBUEG5zG4366+Mo4i/Sc5Uc0lVaiqaZNRyHZkDBFKUmF9dlwxAJCnS/V5G5Q5+lzmXIc1VCM2axp1GpnWw3qd02HAU/wCnT6uT0a9XsbOr3TdRoqgsoCjgAAPcIET4520p0ah29KpanTHjfp+5TKcJhslyTmZjd2ta52AAXNlA0A/2SSaIgIiICIiAiIgIiICIiAiIgIiICIiAiIgIiICIiAiIgIiICIiAiIgIiICIiAiIgIiICIiAiIgIiICIiAiIgIiICIiB/9k=[/img]
SIEMPRE PUEDES VERIFICAR QUE LA HIPOTENUSA ESTA EN POSICION OPUESTA AL ANGULO RECTO, EN CUALQUIER TRIANGULO RECTANGULO
ALGUNAS APLICACIONES QUE PUEDES ENCONTRAR: [br][br][br][table][tr][td]Construcción y carpintería[/td][td]Verificar ángulos correctos en paredes o estructuras [url=https://www.unschoolingmom2mom.com/unschooling-the-pythagorean-theorem?utm_source=chatgpt.com]unschoolingmom2mom.com[/url][/td][/tr][tr][td]Navegación/GPS[/td][td]Calcular rutas directas y posicionamientos [url=https://www.unschoolingmom2mom.com/unschooling-the-pythagorean-theorem?utm_source=chatgpt.com]unschoolingmom2mom.com[/url][/td][/tr][tr][td]Jardinería o urbanismo[/td][td]Trazar sendas diagonales o delimitar parcelas [url=https://www.unschoolingmom2mom.com/unschooling-the-pythagorean-theorem?utm_source=chatgpt.com]unschoolingmom2mom.com[/url][/td][/tr][tr][td]Arquitectura e ingeniería[/td][td]Diseño de techos, cerchas, vigas diagonales [url=https://www.numberanalytics.com/blog/pythagorean-theorem-real-world-applications?utm_source=chatgpt.com]Number Analytics[/url][/td][/tr][tr][td]Tecnología y videojuegos[/td][td]Detección de colisiones, distancias en gráficos 3D [url=https://www.numberanalytics.com/blog/pythagorean-theorem-real-world-applications?utm_source=chatgpt.com]Number Analytics[/url][/td][/tr][/table][br][br][br][br][br][br]ahora escribe en tu cuaderno los objetivos del nuestro taller de aprendizaje.

