[size=85][size=100]Let [math]z=r\left(cos\left(\phi\right)+isin\left(\phi\right)\right)[/math] be a complex number and [b][i]n[/i][/b] any integer. Then [/size][size=100][br][b][color=#ff0000]z[sup]n[/sup]=(r[sup]n[/sup])([i]cos[/i](n[/color][/b][math]\phi[/math][b][color=#ff0000])+i[i]sin[/i](n[/color][/b][math]\phi[/math][b][color=#ff0000]))[br][/color][/b][b][color=#0000ff][u]NOTE: [/u][/color][/b][left][size=85][size=100]In calculating the powers of complex numbers, a complex number z=a+bi must be written in [b][color=#980000]polar form[/color][/b].[br]Then, you can find [b][i]z[/i][sup]n[/sup][/b] as the complex number[br][/size][/size][/left][list=1][*] whose absolute value is [b][color=#1155cc]|[i]z[/i]|[sup][i]n[/i][/sup][/color][/b], the [i]n[/i][sup]th[/sup] power of the absolute value of [i]z[/i],[/*][*] whose [u]argument [/u]is [i]n[/i] times the argument of [i]z.[/i][/*][/list][/size][/size]
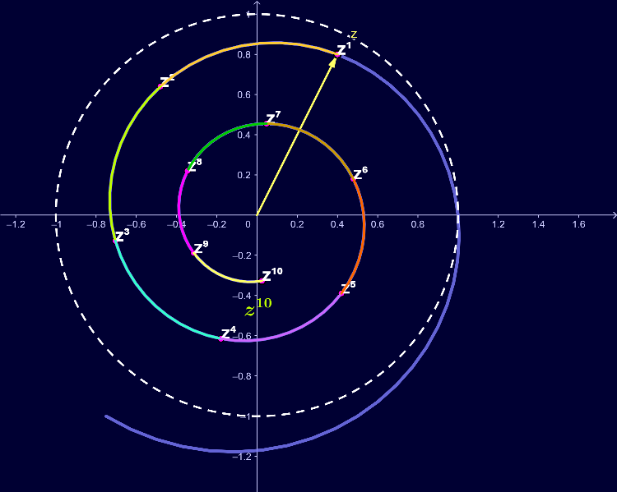
[size=100]In the figure you see a complex number [i][b][color=#0000ff]z[/color][/b][/i] whose absolute value is [b]|[i]z[/i]| = 0.89[/b], and whose argument is [b]63.43°[/b]. Here, the unit circle is dotted white. Since |[i]z[/i]| is less than one, it ’is within unit circle and its square is at 126.87° and [b][color=#6aa84f]closer [/color][/b]to 0. [u]Each higher power is 63.43° further along and even closer to 0.[/u] The first 10 powers are displayed, as you can see, as points on a [b][color=#ff0000]spiral[/color][/b]. [/size]
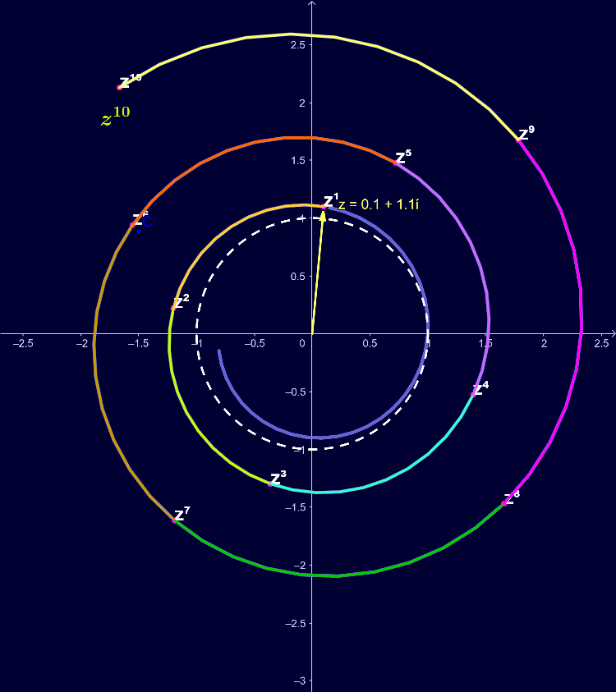
[size=100]The second figure shows the complex number z whose absolute value is |z| = 1.1, and whose argument is 84.81°. Since [b][color=#0000ff]|z| is greater than one[/color][/b], it is outside the unit circle. Each higher power is 84.81° along and [b][u]away from 0[/u][/b].[/size]
[b][color=#0000ff][size=100][size=150]Activity:[/size][/size][br][/color][/b]The following applet you can use to show the spiral of powers.[br]Move the sliders a and b to test for different complex numbers.

