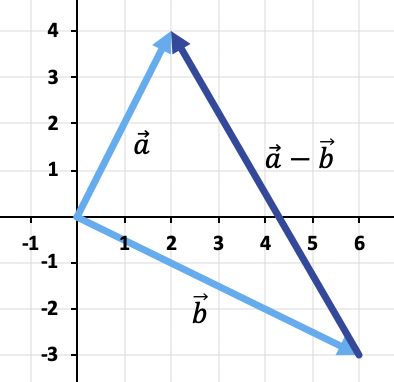
La noción de [b]resta de vectores[/b] se emplea en las [url=https://definicion.de/matematicas/][b]matemáticas[/b][/url]. En este caso, el vector es una magnitud que se grafica como un segmento que tiene su origen en un [b]punto A[/b] y se orienta hacia su extremo (el [b]punto B[/b]). El vector, por lo tanto, es un [b]segmento AB[/b].[br]La resta de vectores es una operación que se realiza con dos de estos [url=https://definicion.de/segmento/][b]segmentos[/b][/url]. Para realizar la resta de dos vectores, lo que se hace es tomar un rector y [b]sumarle su opuesto[/b]

Supongamos que deseamos realizar la siguiente resta: [i]AB – DE[/i], siendo [i]AB (-3, 4)[/i] y [i]DE (5, -2)[/i] de acuerdo a la posición de los vectores en el [url=https://definicion.de/plano-cartesiano/][b]plano cartesiano[/b][/url]. Teniendo en cuenta lo dicho sobre la suma del opuesto, deberíamos plantear la operación de este modo:[br][i](-3, 4) – (5, -2)[br](-3-5, 4+2)[br](-8, 6)[br][/i][br]Como se puede apreciar, a [i]-3[/i] le sumamos el opuesto de [i]5[/i] (es decir, [i]-5[/i]), mientras que a [i]4[/i] le sumamos el opuesto de [i]-2[/i] (o sea, [i]2[/i]). Así, el resultado de esta resta de vectores es [i](-8, 6)[/i].