2016-2 Planteamiento y solución de Problemas (Psol) 2016-2
En este espacio se encuentran las actividades interactivas que se usarán para el curso electivo PSOL, en formato semanal.
Table of Contents
- Semana 1
- Semana1 Sesión 1: ¿ -2 x -3 es igual a +6 ?
- Semana 1 Sesión 2: Promedio de dos viajes
- Paper folding - finding the square root of n
- Domain and Range of a Function
- Domain and range of real functions
- Semana 2
- Suma de áreas poligonales (adaptado de Judah Schwartz)
- La escalera deslizante (Adaptado de Judah Schwartz)
- Semana 3
Semana1 Sesión 1: ¿ -2 x -3 es igual a +6 ?
Semana 1 Sesión 1
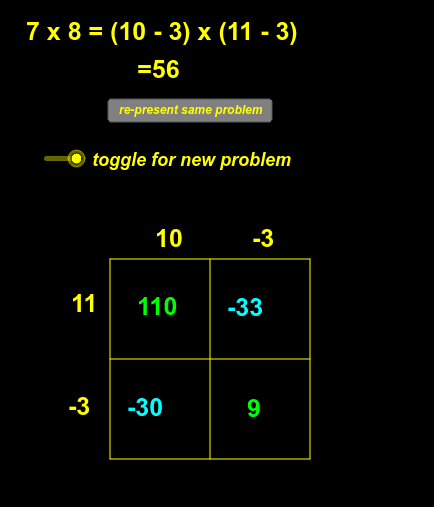
¿Puedes usar este applet para encontrar un argumento que explique por qué[br]menos por menos es más? (Adaptado de [url=https://www.geogebra.org/m/QPQkXr4p]Judah Schwartz[/url] )
Suma de áreas poligonales (adaptado de Judah Schwartz)
The GOLD dot is connected to all four vertices of a rectangle. [br]You can set the size & shape of the rectangles by dragging the GRAY dot.[br]You can place the GOLD dot anywhere in the rectangle.[br][br]The length of the segment from each vertex of the rectangle to the GOLD dot is the side of a regular polygon.[br][br]The sum of the areas of the BLUE polygons is equal to the sum of the areas of the GREEN polygons no matter where you place the GOLD dot. [br][br]Can you prove this? What happens when you drag the GOLD dot outside the rectangle? Why?