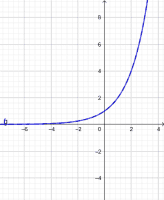
Die allgemeine Exponentialfunktion
In allgemeiner Form kann eine Exponentialfunktion wie folgt geschrieben werden: [br][math]f\left(x\right)=b\cdot a^x[/math][br]Wir werden uns nun der Reihe nach den Einfluss der Parameter a und b erarbeiten.
Der Parameter a:
Welche Einfluss hat der Parameter a (auch Wachstumsfaktor genannt) auf den Graphen von f. Nutze den Schieberegler, um den Einfluss zu untersuchen[br][br]Übertrage anschließend den Graphen für [math]a=\frac{1}{2}[/math] und [math]a=3[/math] und fülle den Lückentext aus. [br]
Der Parameter b:
Welche Einfluss hat der Parameter b (auch Anfangswert oder Startwert genannt) auf den Graphen von f. Erstelle diesmal selbst ein geeignetes Applet mit Schieberegler. Verwende als Wachstumsfaktor a =1,25. [br][br]Tipp: Wenn du den Funktionsterm f(x) = b*1.25^x eingibst, wird automatisch ein Schieberegler erstellt. [br][br]Übertrage das Diagramm für die Fälle b = 2, b = 3 und b = -1 und ergänze dann die Lücken in den Sätzen.
Negative Exponenten
Erstelle ein geeignetes Applet, um herauszufinden, wie ein negativer Exponent den Graphen beeinflusst. [br][br]Vergleiche dazu die Graphen von [math]f\left(x\right)=2^x[/math]und [math]g\left(x\right)=2^{-x}[/math]. [br][br]Finde dann einen geeigneten Wachstumsfaktor, sodass der Graph von [math]h[/math] mit [math]h\left(x\right)=a^x[/math] und der Graph von [math]g[/math] mit [math]g\left(x\right)=2^{-x}[/math] identisch sind. Begründe deine Beobachtung algebraisch (rechnerisch). [br][br]Ergänze die Rückseite des Arbeitsblatts entsprechend.
Vertiefung für Schnelle:
Vergleiche die Graphen der Funktion f mit [math]f\left(x\right)=3\cdot3^x[/math] und [math]g\left(x\right)=3^{x+1}[/math]. Was fällt auf? Begründe deine Beobachtung wieder algebraisch. [br][br]
Wie muss b in Abhängigkeit von c gewählt werden, damit gilt [math]b\cdot a^x=a^{x+c}[/math]?
Wie muss c in Abhängigkeit von b gewählt werden, damit gilt [math]a^{x-c}=b\cdot a^x[/math]
Mehrfache Nullstellen
Vom Funktionsterm einer ganzrationalen Funktion lässt sich nur das Verhalten des Graphens für sehr große x-Werte ablesen. [br][br]
Beschreibe das Verhalten des Graphen im Unendlichen. [br][math]f\left(x\right)=-3x^7+5x^5-x^4+100x^2-5050[/math]
Nur der Leitkoeffizient (Koeffizient der Potenz mit dem größten Exponenten) sowie der größte Exponent ist wichtig. Folglich muss man hier nur wissen, wie der Graph der Potenzfunktion g mit [math]g\left(x\right)=-3x^7[/math] aussieht.
Ausnutzen der Nullstellen
Ein wesentliches Merkmal jedes Graphen sind die Nullstellen. Kennt man diese kann man den Funktionsterm in die "Nullstellenform" bringen. [br][br]z.B. bei quadratischen Funktionen: [math]f\left(x\right)=2x^2+6x+4=2\left(x+2\right)\left(x+1\right)[/math][br]oder bei Grad 7: [math]g\left(x\right)=-2x^7-10x^6+72x^5+96x^4-96x^3-96x^2-256x-128=-2\left(x-2\right)^2\left(x+2\right)^4\left(x+1\right)[/math][br][br]Gib jeweils die Nullstellen an.
Erklärung:
Liegt der Funktionsterm in der faktorisierten Form vor, genügt, es die einzelnen Faktoren (-> Klammern) zu untersuchen. Denn ist einer der Faktoren Null, so ist auch das gesamte Produkt Null.
Einfluss der Exponenten in der Nullstellenform
Untersuche nun, welchen Einfluss der Exponent auf die jeweilige Nullstelle hat. Verschiebe dazu die Schieberegler.
Es lassen sich zwei Verläufe unterscheiden.

Beim Exponenten der jeweiligen Nullstlle spricht man auch von der Vielfachheit der Nullstelle. [br][br]Bsp: [math]f\left(x\right)=0,5\left(x-7\right)^3\left(x-3\right)^8[/math][br]Hier hätte die Nullstelle [math]x_1=3[/math] die Vielfachheit 8 und die Nullstelle [math]x_2=7[/math] die Vielfachheit 3.
Die Erklärung des Verhaltens ist recht simpel. Betrachtet man nur die Umgebung der Nullstelle, ist der Einfluss des entsprechenden Faktors in der Nullstellenform am größten. [br][br]Bsp: [math]f\left(x\right)=0,8\cdot\left(x-3\right)^4\left(x+5\right)^3[/math][br][br]Betrachten wir hier nur die Umgebung um [math]x=3[/math] hat der Term [math]\left(x-3\right)^4[/math] den größten Einfluss. Das heißt, bei dieser Nullstelle verhält sich der Graph wie der einer Potenzfunktion vom Grad 4. Mit diesem Vorgehen lässt sich der gesamte Graphenverlauf zusammenbauen.
Graphen skizzieren
Mit diesem Wissen können wir nun den Graphen einer ganzrationalen Funktion schon genauer zeichnen.
Hefteintrag
Übernimm nun den Hefteintrag. Skizziere dabei den Verlauf des Graphen unter Beachtung des Verhaltens im Unendlichen und um die Nullstellen. [br][br]Wichtig: Den genauen Verlauf können wir so natürlich nicht zeichnen.
Erarbeitung der allgemeinen Sinusfunktion
Beschreibe, wie der Graph der Funktion f mit [math]f\left(x\right)=-2\left(x-2\right)^2+3[/math] aus der der Normalparabel ([math]g\left(x\right)=x^2[/math]) hervorgeht.
Überprüfe dein Wissen nochmal mit dem Applet, indem du die Schieberegler verschiebst.
Transformationen der Sinus-Funktion:
[br][br]Stelle zunächst Vermutungen auf, wie der Graph der folgenden Funktionen aus dem Graph von f: x↦sin(x) hervorgeht. [br][br][math]g_1:x\mapsto sin\left(x\right)+2[/math][br][math]g_2:x\mapsto sin\left(x+\frac{\pi}{2}\right)[/math][br][math]g_3:x\mapsto2sin\left(x\right)[/math][br][math]g_4:x\mapsto sin\left(2x\right)[/math][br][br]
[math]g_1[/math]
[math]g_2:[/math]
[math]g_3:[/math]
[math]g_4:[/math]
Überprüfe nun deine Vermutung durch Ausfüllen der Wertetabelle und Zeichnen der Graphen auf dem Arbeitsblatt.
Kugel - Würfel - Schachtelung
Der große Würfel hat die Kantenlänge a. Darin einbeschrieben ist eine Kugel, d.h. die Kugel berührt gerade so alle Seitenflächen des Würfels. In der Kugel ist wiederum ein Würfel einbeschrieben, d.h. die Ecken liegen genau auf der Kugeloberfläche. Usw. ...[br][br]a) Bestimme die Radien der Kugeln sowie die Kantenlänge des inneren Würfels in Abhängigkeit von a. [br]Vorgehen: [br]1) Betrachte schrittweise immer nur einen Körper, sowie den darin einbeschriebenen für mehr Übersichtlichkeit. [br]2) Suche eine Ansicht, sodass die Zusammenhänge am besten zu erkennen sind. [br]3) Nutze dann die üblichen Instrumente wie Pythagoras, ... [br][br]b) Bestimme die Volumina und die Oberflächeninhalte der Kugeln/Würfel. Vergleiche die Ergebnisse.
Zusatz für Schnelle:
Stelle einen Funktionsterm auf, der das Volumen des n-ten Würfels angibt und plotte ihn im Graphikrechner. Wähle a = 1.