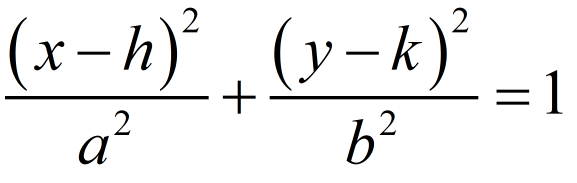La Elipse Actividad 4
INICIO
[br][justify]Usa la gráfica anterior, para realizar las acciones indicadas y responder las preguntas correspondientes.[/justify][justify][b]1º[/b] Desplaza el punto Q libremente, y observa el valor de las sumas de distancias a dos puntos fijos F[sub]1 [/sub]y F[sub]2[/sub] que está calculado en la parte superior.[/justify][justify]¿Esta suma de distancias puede tomar cualquier valor?[/justify][justify]Determina cuál es el valor mínimo de esta suma e indica la posición del punto.[/justify]
¿Esta suma de distancias puede tomar cualquier valor?
Determina ¿Cuál es el valor mínimo de esta suma? e indica la posición del punto.
[b]2º[/b] Desplaza el punto P y comprueba que ocurre con la suma de distancias a F[sub]1[/sub] y F[sub]2[/sub] ([b]FOCOS[/b]) que está calculado en la parte superior derecha.
Al variar las posiciones de este punto P se obtiene la [b]ELIPSE[/b]. Defínela como lugar geométrico.[br]
¿Tiene algún tipo de simetría la elipse? ¿por qué?[br]
¿Qué cumplen los puntos que no están situados en la elipse?
[b]3º[/b] Para representar una elipse particular se han fijado los dos focos en el eje de abscisas a una distancia [b]c[/b] de 4 unidades, cada uno, del origen de coordenadas. Y se ha fijado la suma de distancias a los focos como 10 unidades.
Determina el valor de [b]a[/b] ([b]SEMIEJE MAYOR[/b]) en función del valor de la suma de distancias de los puntos de la elipse a los focos. (Para justificarlo puedes situar el punto P sobre A)[br]
¿Qué relación hay entre a, b y c? . (Para justificarlo puedes situar el punto P sobre B)[br]
Determina el valor de [b]b[/b] ([b]SEMIEJE MENOR[/b]) en función de a y c.
DESARROLLO
[justify]La proporción o cociente entre c y a se llama [b]EXCENTRICIDAD[/b], [b]e[/b] = c/a[br]Si mantenemos el valor de [b]a[/b]=5 , observa al modificar el valor de [b]b,[/b] con el deslizador situado en la parte inferior derecha, observe cómo varían los focos y la forma de la elipse para responder las siguientes preguntas:[/justify][br]
¿Qué ocurre cuando a=b?[br]
¿Entre qué valores varía la excentricidad?[br]
¿Qué interpretación podemos dar a la excentricidad?
[b]4º[/b] En la parte superior izquierda se muestra la ecuación de la elipse para el caso a=5 y b=3. Modifica el valor de b, y deduce la ecuación de la elipse.
Para el caso anterior, escribe la ecuación obtenida y el valor de a y b usados.
[b]5º[/b] En la parte superior izquierda se muestra la ecuación de la elipse para el caso a=5 y b=3. Modifica el valores de a, b y c para responder lo siguiente:
¿Qué sucede si a<b?
¿Qué sucede si a>b?
CIERRE
[justify] Las elipses vistas hasta ahora estaban centradas en el origen de coordenadas, la ecuación vista es la forma canónica.[br][br][b]6º[/b]Si desplazamos la elipse situando el centro con los deslizadores situados en la parte inferior izquierda, se mantienen sus valores característicos a, b, c, e y sus relaciones. Los vértices y focos habrán sido desplazados. Compruébalo en diferentes casos y observa su ecuación.[br][br][/justify]
¿Qué sucede si a=b?

Una ecuación cómo las observadas se denomina [b]ecuación de la elipse horizontal con centro fuera del origen[/b] y se representa como se muestra en la imagen inferior siendo las coordenadas del centro [math]C\left(h,k\right)[/math].