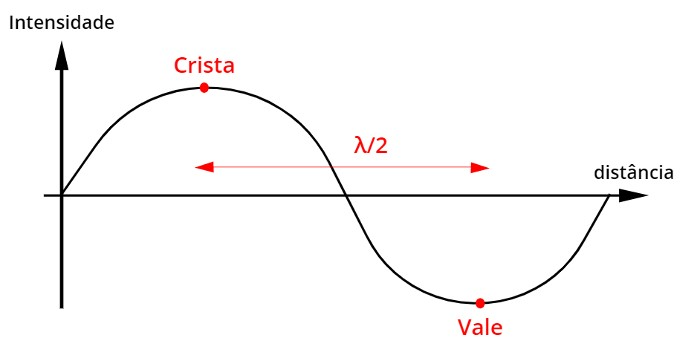
O som é uma onda mecânica, pois só é capaz de propagar-se em meios físicos como ar, água, metal etc. Sendo uma onda, o som apresenta propriedades, como[br]Velocidade de propagação, comprimento de onda, frequência e amplitude:[br][br]A velocidade (v) do som depende do meio no qual ele é propagado, meios físicos de maior elasticidade tendem a propagar o som com mais facilidade, em razão da proximidade entre as suas moléculas.[br][br]A frequência (f) de uma onda sonora é medida em Hz, essa frequência define a sua altura, isto é, quanto maior é a frequência do som, mais agudo, ou alto, esse som é.[br][br]O comprimento de onda (λ) do som é o espaço necessário para que a onda sonora produza uma oscilação completa, também pode ser entendido como a distância entre duas cristas ou dois vales de uma onda.[br][br]A amplitude da onda sonora define a sua intensidade, ou a quantidade de energia que essa onda carrega consigo, que também pode ser entendida como o “volume do som”.[br]

A figura acima relaciona a intensidade da onda sonora com a distância que ela percorre.[br]Mostrando semelhança com o gráfico da função seno, já que a curva entre ambos os gráficos são identicos.

A atividade a seguir, mostra na prática a aplicação da função seno nas ondas sonoras. As informações abaixo relatam o significado de cada ferramenta da atividade, com relação a função seno: [br][br]O ponto A caracteriza-se por mostrar o valor da amplitude da função, ou seja, o quanto a curva sobe ou desce em relação ao eixo das ordenadas (eixo y). [br][br]O ponto B altera o período da função, ou seja, altera a distância dos pontos que cortam o eixo das abcissas (eixo x). [br][br]O ponto C causa o deslocamento lateral da função.

Com essa atividade acima, podemos ver o gráfico de seno mas com uma peculiaridade diferente.[br]Nele mostra uma ondulação em que pode mexe-lá, para os lados e no tamanho de sua encurvadura entre os extremos de Y(-1 até 1).[br]Então mostra uma frequência, um som especifico, que pode ser considerado uma nota, como por exemplo: se deixar os valores de A=1, B=440 e C=0, podemos escutar uma frequência que denominamos de Lá.

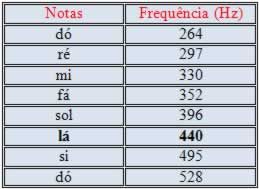
Então denominamos a frequência como valores de B. Portanto, para trocarmos e tocarmos outra nota é preciso alterar o valor de B.