El número e
[br][br][b]¡Es un real, irracional, trascendente o infinito! [/b][br][br][br]INTRODUCCIÓN[br]El número de [b]e[/b], también conocido como [b]número de [i]Euler[/i][/b] o [b]constante de [i]Napier [/i][/b] [br]Junto con [math]\pi[/math] y [math]\phi[/math]se consideran números irracionales, reales, trascendente e infinitos[br]Sus valores aproximados son: 2,7182818284590452353602874713527[b]….[/b] [br][br]HISTORIA[br]Descubierto por Jacob Bernoulli (interés compuesto)[br]1618: primeras referencias de e sobre logaritmos de John Napier[br]1736: Leonhard Euler introduce e en su publicación [i]mechanica[/i] [br][justify]El “abuelo” de [b][i]e[/i][/b] fue John Napier, quien nació en 1550 en Edimburgo. Él fue el primero en definir y trabajar con los logaritmos ([i]Mirifici Logarithmorum Canonis Descriptio[/i], 1614) o números artificiales como los llamó, con lo cual se simplificaron los cálculos matemáticos y fue posible realizar otros, ya que las multiplicaciones se pueden sustituir por sumas, las divisiones por restas, las potencias por productos y las raíces por divisiones.[br]La idea de Napier para concebir los logaritmos fue la comparación entre 2 progresiones, una aritmética y una geométrica. Años después fueron publicadas, en un apéndice al trabajo de Napier, unas tablas de logaritmos naturales de varios números pero en base [i]e[/i], aunque aún no se reconocía como una constante.[br]El símbolo [i]e[/i] hace su aparición en una carta que escribió Leonhard Euler a Goldbach en 1731. [br]Euler realizó varios descubrimientos en torno a [i]e[/i] y en 1748 publicó su obra [i]Introductio in analysin infinitorum.[/i][/justify][br]Proporcionó un análisis completo y demostró que: [b][i]e [/i]= 2.7182818284590452[/b][br][br] [justify][b][i]e[/i][/b] puede ser definido de manera algebraica mediante fracciones continuas que es lo que expresó Euler, pero también puede ser representado como una serie infinita [br][/justify][br]
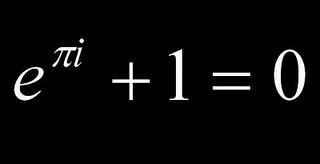
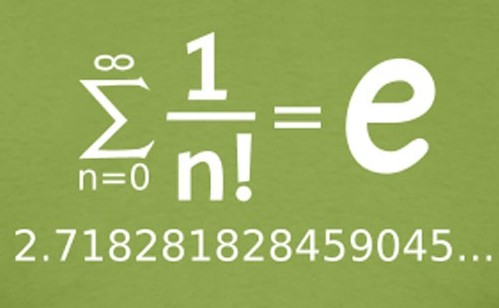
¿Cuál es el nombre correcto del país que habitamos?
De la fórmula general para ecuaciones de segundo grado ¿cual es la expresión denominada discriminante?

