[b]A particle moves along a straight line. At time t seconds after it starts moving,its displacement, s m, from a fixed point O is given by s = 3 + 2t – t[/b][sup]2[/sup][b] , where t is time,in seconds.[/b][size=150][size=100][b]a) Determine the velocity function, v, and acceleration function, a, of the particle.[/b][/size][size=150][size=150][size=100][b]b) On the same diagram, sketch a graph of function s, v and a for [/b][b][b][size=150]0≤ t ≤3 [/size][/b][/b][b]and explain the motion of the particle from point O for that interval.[/b][/size][/size][/size][/size]

[b]Solution[/b][br][size=100][size=150][sup][size=150][/size][/sup][/size][/size][size=150][sup][size=150]a) [/size][/sup][/size]

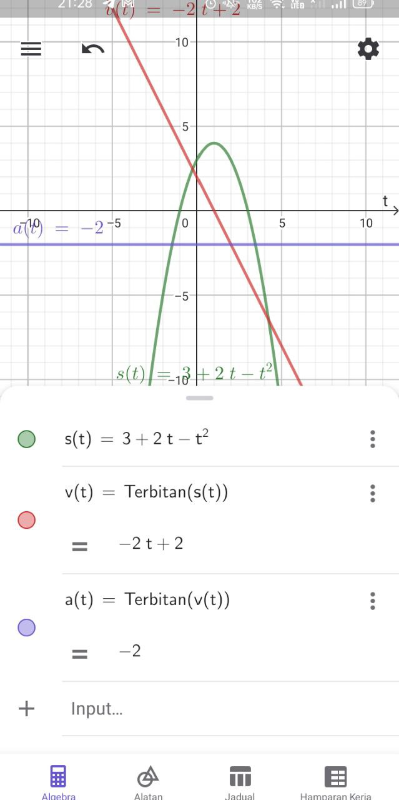
[size=100][br]Hence, the velocity function at time t , v=2-2t and acceleration function at time t ,a=-2ms[sup]-2[/sup][/size][sup][size=100][i][sup][br][br][/sup][/i][/size][/sup]b)

[size=150][size=100][size=150]Graph of the displacement, velocity, and acceleration functions of a particle that moves from the the fixed point O can be simplified on a number line as follows:[/size][/size][/size]

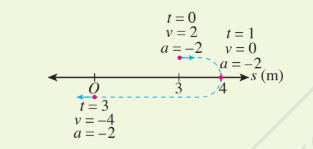
[justify][size=100]From the graph and the number line:[br][/size][/justify][list][*][size=100]It is found that the displacement of the particle at t=0 from the fixed point O is 3m, the initial velocity is 2ms[sup]-1[/sup] and acceleration is -2ms[sup]-2[/sup]. [/size][/*][*][size=100]At t=1, the particle changes its direction of motion, the displacement from the fixed point O is maximum, which is 4 m, the velocity is 0 ms[sup]-1[/sup] and the acceleration is −2 ms[sup]-2[/sup]. [/size][/*][*]At t=3, the particle reaches to the fixed point O where its displacement is 0 m, velocity is −2 ms[sup]-1[/sup], and its acceleration is the same, which is −2 ms[sup]-2[/sup]. [/*][*][size=100]The total distance traveled by the particle from t=0 to t = 3 is (4−3)+4=5 m. [/size][/*][/list]