Reelle Zahlen
Lernbuch zu "Menge der reellen Zahlen"
Table of Contents
- Grundlagen
- Rationale Zahlen am Beispiel erklärt
- Achse beschriften
- Wurzel 2 auf der Zahlengeraden
- Erklärvideo: Wurzel 2 auf der Zahlengeraden
- Wurzel2 an der Zahlengeraden darstellen
- Menge IR der reellen Zahlen
- Erklärvideo: Menge IR der reellen Zahlen
- Wurzel 2 ist irrational.
- Erklärvideo: Wurzel 2 ist irrational
- Heron-Verfahren
- Erklärung zu Heron
- Der goldene Schnitt
- Der Goldene Schnitt
- Konstruktion des goldenen Schnitts
- Das regelmäßige 5-Eck und der Goldene Schnitt
- Das regelmäßige 5-Eck konstruieren mit Zirkel und Lineal
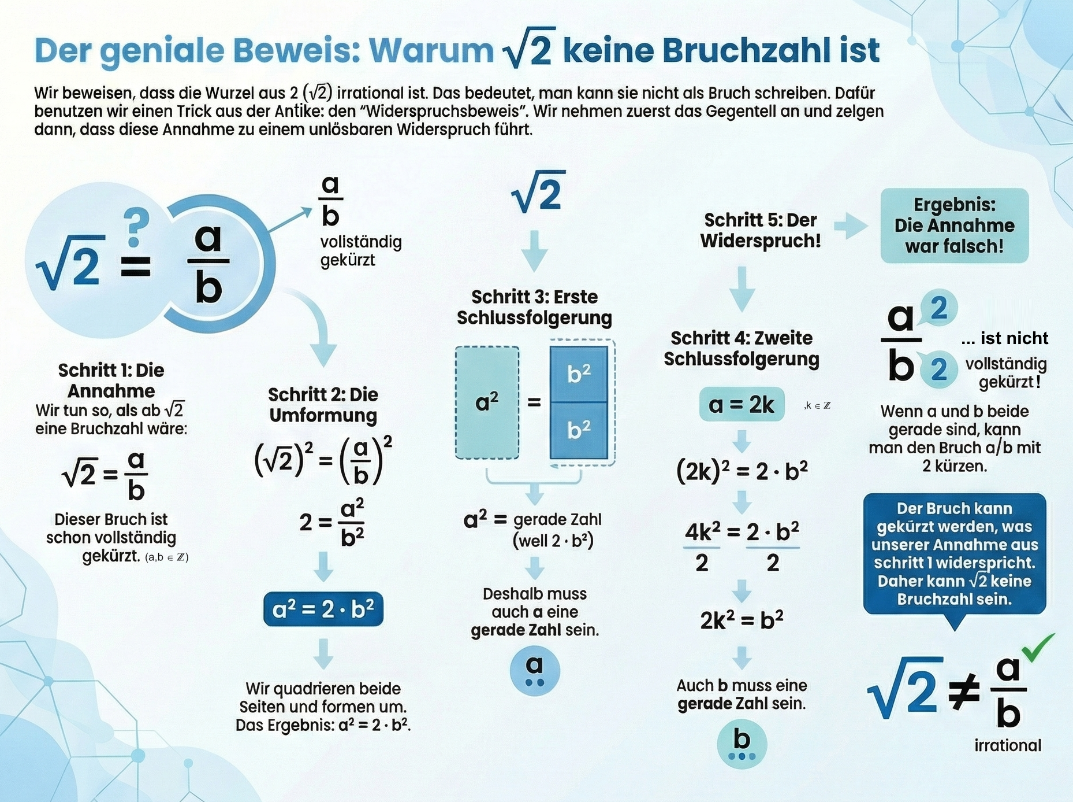
Rationale Zahlen am Beispiel erklärt
Kreuze alle rationalen Zahlen (Bruchzahlen) an.
Erklärvideo: Wurzel 2 auf der Zahlengeraden
Erklärvideo: Menge IR der reellen Zahlen
Erklärvideo: Wurzel 2 ist irrational
Erklärung zu Heron
Das folgende Video kann mit diesem Applet nachvollzogen werden.
Prof. Dr. Edmund Weitz (von der Hochschule für Angewandte Wissenschaften Hamburg) erklärt das Heron-Verfahren:
Der Goldene Schnitt
Das Bild zeigt die Konstruktion des Goldenen Schnitts.
Bereits 300 v.Ch. definierte Euklid in seinem Werk [i]Die Elemente[/i] den Goldenen Schnitt zu ersten Mal:[br][br]"Eine gegebene Strecke ist so zu teilen, dass das Rechteck aus der ganzen Strecke und dem einen Abschnitt ([math]a\cdot m[/math]), dem Quadrat über dem anderen Abschnitt ([math]M^2[/math]) gleich ist."[br][br][b]Die moderne Definition des Goldenen Schnitts:[br]Sei [math]a=|\overline{AB}|[/math] eine Strecke. Ein Punkt G von a teilt a im Goldenen Schnitt, wenn sich die größere Teilstrecke M (Major) zur kleineren m (Minor) verhält, wie die Gesamtstrecke zum größeren Teil.[br][/b][br][math]\frac{a}{M}=\frac{M}{m}\Longrightarrow am=M^2[/math][br][br]Diese Umformung zeigt wunderschön, wie die historische ([math]am=M^2[/math]) und die moderne ([math]\frac{a}{M}=\frac{M}{m}[/math]) Definition zusammenhängen.[br][br][br][br][size=150]Mit diesem Applet kannst du den [b]Goldenen Schnitt[/b] experimentell bestimmen:[br]Du kannst den [color=#BF9000][b]Punkt G[/b][/color] und die Punkte A und B bewegen.[/size]
Quellen und interessante Links: [br][list][/list][list][*][url=http://www.uni-hildesheim.de/~stegmann/goldschn.pdf]http://www.uni-hildesheim.de/~stegmann/goldschn.pdf[/url][/*][*][url=https://www.br.de/mediathek/video/mathematik-zum-anfassen-der-goldene-schnitt-av:5d138dd1c8960b00190bd8d6]Mathematik zum Anfassen: Der Goldene Schnitt[br][/url][/*][/list][br]Der [b]Goldene Schnitt[/b] ist Teil des neuen LehrplanPlus (M9I; LB2).