Gegeben ist die Funktion [math]f\left(x\right)=\frac{1}{2}\cdot x^2+1[/math].[br]Es soll ein Verfahren entwickelt werden, wie man den Inhalt der Fläche zwischen Graph und [math]x[/math]-Achse im Intervall [math][0;b][/math] bestimmen kann.

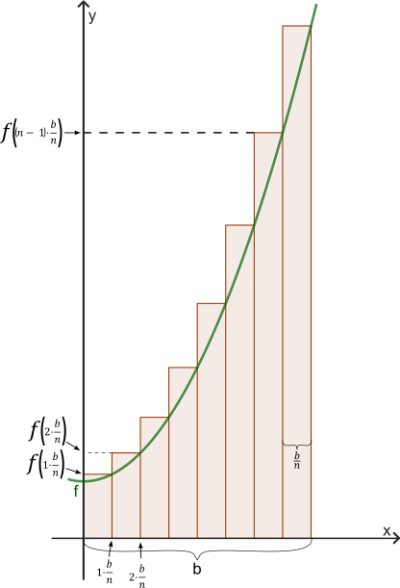
[br][br]Für jeden Wert von b kann man den Inhalt der Fläche zwischen dem Graphen von [math]f[/math] und der [math]x[/math]-Achse durch die [b]Ober[/b]- und die [b]Untersumme[/b] annähern.[br]Aber könnte man auch allgemein eine Funktion finden, die den Flächeninhalt zwischen Graph und [math]x[/math]-Achse im Intervall [math][0;b][/math] beschreibt?[br][br][u]Beachte die folgenden zwei Hinweise:[/u][br][br][b]1. [/b]Der Flächeninhalt der [b]Obersumme[/b] ist die Summe der Flächeninhalte der einzelnen Rechtecke, deren rechte oberen Ecken auf dem Graphen von [math]f[/math] liegen. [br]Die Breite der einzelnen Streifen beträgt jeweils [math]\frac{b}{n}[/math] bei [math]n[/math] Streifen.[br]Der Flächeninhalt des [math]i[/math]-ten Streifens ist daher [math]\frac{b}{n}\cdot[/math]Funktionswert an der Stelle [math]\left(i\cdot\frac{b}{n}\right)[/math] .

[b]2.[/b] Für die Summe der ersten [math]n[/math] Quadratzahlen [math]1+4+9+\dots+n^2[/math] gilt[math]\sum_{i=1}^ni^2=\frac{n\cdot\left(n+1\right)\cdot\left(2n+1\right)}{6}[/math] .[br][br](Diesen Sachverhalt kann man mit vollständiger Induktion beweisen, siehe z.B. [url=https://www.arndt-bruenner.de/mathe/Allgemein/summenformel1.htm]hier[/url].)[br][br]Bringe im folgenden Applet die Terme in die richtige Reihenfolge, indem du an den Punkten ziehst und die Terme in den grauen Rechtecken positionierst.[br][color=#1155cc]Schalte dafür das Applet in den Vollbildmodus.[/color]

[u]Anmerkung:[/u] die Berechnung des Flächeninhalts mit der Untersumme erfolgt analog und führt zum selben Ergebnis. [url=https://www.geogebra.org/m/c8jkxrp6]Probiere es hier aus![/url]