Le isometrie sono delle trasformazioni geometriche attraverso le quali l'oggetto di partenza ne mantiene le distanze, infatti mantiene inalterate le caratteristiche misurabili dello stesso, come le misure dei lati, l'ampiezza degli angoli, il perimetro, l'area e il volume.[br]Le isometrie sono sempre state presenti in natura mostrando le più svariate regolarità. Queste vengono sottolineate anche ne "Il Piccolo Principe" di Antoine de de Saint-Exupery come evidenziato nel discorso fra il protagonista ed un fiore, quest'ultimo afferma infatti che in natura esistono innumerevoli simmetrie e che tutto in natura nasce da una simmetria (le stelle marine, i fiori, i fiocchi di neve, i cristalli e l'uomo); le simmetrie possono inoltre essere colte nella disposizione dei colori come appunto in un fiore.[br]Volendo citare un commento al libro "L'Equazione impossibile" dell'astrofisico Livio Mario: “La simmetria è l’elemento principe, la fiaccola, che guida il matematico a scoprire le leggi della[br]natura con il puro intelletto, ancor prima che dedurle dai fatti sperimentali”.[br]Alla regolarità della natura si ispira l’arte utilizzando forme vegetali, si possono creare difatti opere di estrema perfezione come i rosoni e i fregi. Anche i frattali sono figure simmetriche ispirate alla natura (sotto è presente un link fruibile al file .ggb del Merletto di Koch, che ne è un chiaro esempio).[br]Nelle righe precedenti abbiamo evidenziato alcuni esempi di simmetrie, una delle isometrie più conosciute ed utilizzate in ambito artistico, ma ne esistono molte altre che analizzeremo nei prossimi capitoli basandoci su alcuni esempi di opere.
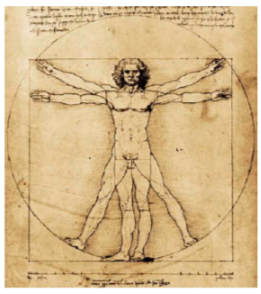
[color=#ff0000][b]L'uomo vitruviano dimostra le simmetrie umane[/b][/color]

[color=#ff0000][b]Rosone della Basilica di S. Croce a Lecce, perfettamente simmetrico![/b][/color]


