Calcolatrice 3D GeoGebra - Tutorial
Ecco la nuova [url=https://www.geogebra.org/3d]Calcolatrice 3D GeoGebra[/url]! Impara a disegnare solidi, visualizzare rotazioni e sezioni in 3D, esplorare gli oggetti nella Realtà Aumentata e molto altro ancora!
Table of Contents
- Primi passi
- App GeoGebra a confronto
- Introduzione
- Esploriamo l'app
- La vista Algebra
- La vista Strumenti
- La vista Grafici 3D
- Realtà aumentata (AR)
- Operazioni di base
- Cilindro e cubo
- Modellare in Realtà Aumentata (AR)
- Rotazioni
- Sezioni di un cono
- Circonferenze in 3D
- Operazioni avanzate
- Triangoli su una sfera
- Quadriche
- Poliedri e simmetrie
- Tutorial su YouTube
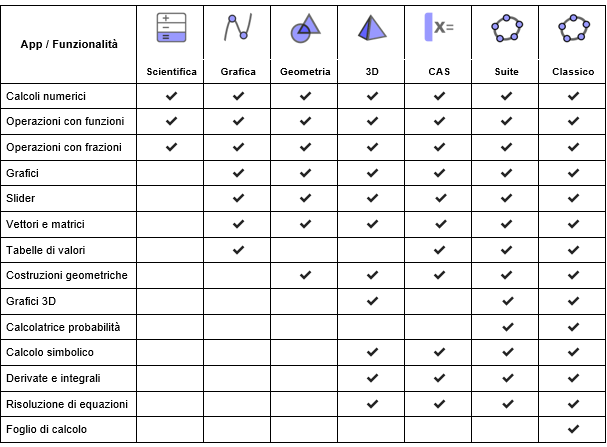
App GeoGebra a confronto
Con le app [i]GeoGebra [/i]è possibile esplorare le funzioni, la geometria, l'algebra, la statistica e lo spazio 3D in un modo nuovo e interattivo.[br][list][*][url=http://www.geogebra.org/scientific]Calcolatrice scientifica[/url][br][/*][*][url=https://www.geogebra.org/graphing]Calcolatrice grafica[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometria[/url][br][/*][*][url=https://www.geogebra.org/calculator]Suite calcolatrici[/url][/*][*][url=https://www.geogebra.org/cas]Calcolatrice CAS[/url][br][/*][*][url=https://www.geogebra.org/3d]Calcolatrice 3D[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Classic[/url][br][/*][/list]L'app giusta per voi è quella che soddisfa le vostre necessità, ed è totalmente compatibile con le restrizioni imposte localmente per gli esami e i test scolastici. La tabella che segue vi offre una panoramica delle funzionalità disponibili per ogni app.
Utilizzare GeoGebra agli esami
Siamo totalmente convinti che per gli studenti sia un beneficio utilizzare esattamente la stessa app [i]GeoGebra [/i]in classe, per lo studio a casa e durante gli esami. In questo modo saranno in grado di esercitarsi e imparare bene il funzionamento dell'app, e quindi sfruttare la tecnologia nel modo migliore in qualsiasi situazione. Ecco perché abbiamo creato la [url=https://www.geogebra.org/m/hvtasyxw]modalità Esame di GeoGebra[/url] e l'abbiamo inserita in ogni app. La [i]modalità Esame[/i] blocca il dispositivo mobile in modo tale che gli studenti non possano comunicare tra loro o utilizzare qualsiasi altra app durante un esame. Questa funzionalità è stata testata sul campo ed approvata da vari ministeri dell'istruzione in varie regioni del mondo. Scopri come [url=https://www.geogebra.org/m/hvtasyxw]utilizzare GeoGebra negli esami[/url].[br][br]Per ulteriori informazioni o domande relative all'utilizzo delle [i]app GeoGebra[/i] e alla [i]modalità Esame[/i], non esitate a contattarci all'indirizzo [url=mailto:support@geogebra.org]support@geogebra.org[/url]
Cilindro e cubo
Attività
Costruisci un cilindro e un cubo.[br][br]Guarda il video e impara come costruire un cilindro e un cubo con la [i][url=https://www.geogebra.org/3d]Calcolatrice 3D GeoGebra[/url][/i]. Quindi segui le istruzioni per ricreare la stessa costruzione passo a passo.
Guarda questo video...
Istruzioni
[table][tr][td]1. [/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Apri le [i]Impostazioni[/i] e seleziona [i]Mostra griglia[/i]. [/td][/tr][tr][td]2.[/td][td][/td][td]Nella [i]vista Algebra[/i][i] [/i]inserisci il comando [math]Cilindro((2,-3,-1),(2,2,2),2)[/math] per creare il cilindro per i due punti indicati e raggio di base 2, quindi premi [i]Invio[/i]. [/td][/tr][tr][td]3.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Esplora diverse [i]Proiezioni,[/i] selezionandole nelle [i]Impostazioni[/i]. [/td][/tr][tr][td]4.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon][/td][td]Passa alla [i]vista Strumenti[i][/i][/i], seleziona lo strumento [i]Punto [/i]e crea due nuovi punti. [/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_cube.png[/icon][/td][td]Attiva lo strumento [i]Cubo [/i]e seleziona i punti creati per costruire un cubo. [/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Seleziona lo strumento [i]Muovi [/i]ed esplora le tue costruzioni. [br][/td][/tr][/table]
Ora prova tu...
Realtà aumentata
Se stai utilizzando la [i]Calcolatrice 3D GeoGebra [/i]su un dispositivo mobile compatibile, puoi passare alla [i]modalità[/i] [i]AR [/i]per posizionare gli oggetti matematici che hai creato su qualsiasi superficie piana (ad es. un tavolo, il pavimento, ...) e muoverti attorno ad essi. Esplora le tue costruzioni da un nuovo punto di vista!
Triangoli su una sfera
Attività
Crea un triangolo su una sfera.[br][br]Guarda il video e impara come costruire un triangolo su una sfera con la [i][url=https://www.geogebra.org/3d]Calcolatrice 3D GeoGebra[/url][/i]. Quindi segui le istruzioni per ricreare la stessa costruzione passo a passo.
Guarda questo video...
Istruzioni
[table][tr][td]1.[/td][td][/td][td]Inserisci nella [i]barra di inserimento[/i] della [i]vista[/i] [i]Algebra [/i] [math]A=(0,0,0)[/math] e quindi il comando [math]Sfera(A,1)[/math] .[/td][/tr][tr][td]2.[/td][td][/td][td]Seleziona la sfera nella [i]vista Grafici 3D[/i] e seleziona [img]https://wiki.geogebra.org/uploads/thumb/d/d5/Color_button.svg/16px-Color_button.svg.png[/img] [i]Colore[/i] nella [i]barra di stile [/i]visualizzata, per modificare il colore della sfera.[br][/td][/tr][tr][td]3.[/td][td][img]https://wiki.geogebra.org/uploads/thumb/d/d2/Ic_settings_black.svg/32px-Ic_settings_black.svg.png[/img][/td][td]Apri le [i]Impostazioni[/i] e deseleziona le opzioni [i]Mostra assi[/i] e [i]Mostra piano.[/i][/td][/tr][tr][td]4.[/td][td][/td][td]Passa alla [i]vista Strumenti. [/i][/td][/tr][tr][td]5.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_point.png[/icon][/td][td]Seleziona lo strumento [i]Punto [/i]e crea tre punti, [i]B[/i], [i]C [/i]e [i]D [/i]sulla sfera. [/td][/tr][tr][td]6.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_circlearc3.png[/icon][/td][td]Attiva lo strumento [i]Arco di circonferenza, [/i]quindi seleziona il centro [i]A[/i] e i punti [i]B[/i] e [i]C[/i]. Ripeti questa operazione con gli altri punti per creare un triangolo sferico (selezionando sempre il punto [i]A [/i]per primo).[br][/td][/tr][tr][td]7.[/td][td][icon]https://www.geogebra.org/images/ggb/toolbar/mode_move.png[/icon][/td][td]Utilizza lo strumento [i]Muovi [/i]per trascinare i puti sulla sfera ed esplorare la costruzione.[br][/td][/tr][/table]
Ora prova tu...
Realtà aumentata
Se stai utilizzando la [i]Calcolatrice 3D GeoGebra [/i]su un dispositivo mobile compatibile, puoi passare alla [i]modalità[/i] [i]AR [/i]per posizionare gli oggetti matematici che hai creato su qualsiasi superficie piana (ad es. un tavolo, il pavimento, ...) e muoverti attorno ad essi. Esplora le tue costruzioni da un nuovo punto di vista!