数式処理(CAS) を学ぶ
[url=https://www.geogebra.org/cas]GeoGebra 数式処理（CAS）[/url]へようこそ! このチュートリアルでは、方程式の解き方、式の展開と因数分解、微分と積分の求め方など、さまざまなことを学びます。
İçindekiler
- はじめに
- GeoGebra数学アプリの比較
- 序論
- アプリの紹介
- 基本
- 関数の定義
- 項と変数
- 方程式と不等式を解く
- 連立方程式を解く
- 関数の極限
- 微分の計算
- 定積分と不定積分
- 応用
- 有理関数
- 回転体の体積
- 曲線のスケッチ
- ４次関数
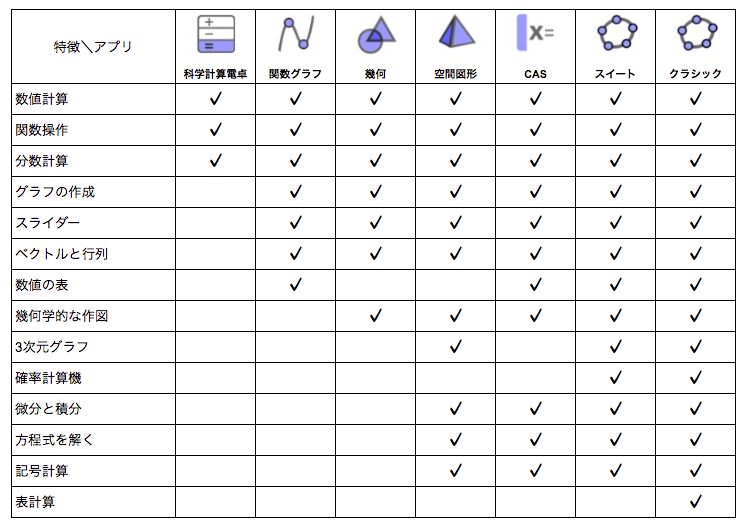
GeoGebra数学アプリの比較
[i]GeoGebra[/i]の数学アプリケーションを使えば、関数、幾何学、代数、統計、3Dを新しいインタラクティブな方法で探求し、学ぶことができます。[br][list][*][url=http://www.geogebra.org/scientific]科学計算電卓（Scientific Calculator[/url]）[/*][*][url=https://www.geogebra.org/graphing]関数グラフ（Graphing Calculator[/url]）[/*][*][url=https://www.geogebra.org/geometry]幾何（Geometry[/url]）[br][/*][*][url=https://www.geogebra.org/calculator]GeoGebra スウィート（Calculator Suite[/url]）[/*][*][url=https://www.geogebra.org/cas]数式処理(CAS)（CAS Calculator[/url]）[/*][*][url=https://www.geogebra.org/3d]空間図形（3D Calculator[/url]）[/*][*][url=https://www.geogebra.org/classic]クラシック６（全機能版Webアプリ）（GeoGebra Classic[/url]）[br][/*][/list]自分に合ったアプリとは、自分のニーズを満たし、テストで使用する場合は、地域で定められている試験規定を満たしているアプリです。次の表は、どのアプリでどのような機能が利用できるかの概要です。
試験におけるGeoGebra
私たちは、生徒が授業中、宿題、テスト中にまったく同じGeoGebraアプリを使用することが有益であると考えています。そうすれば、アプリで最も多くの練習をすることができ、したがって、あらゆる状況で私たちのテクノロジーを最大限に活用することができるようになります。そのため、私たちは[url=https://www.geogebra.org/m/y3aufmy8]GeoGebra試験モード[/url]を作成し、各アプリの中に追加しました。試験モードでは、モバイルデバイスをロックして、試験中に生徒が通信したり、GeoGebra以外のアプリを使用できないようにしています。この方法は、すでにいくつかの地域の教育省が実地テストを行い、承認しています。GeoGebraを試験で使用する方法について、詳しくは[url=https://www.geogebra.org/m/y3aufmy8]こちら[/url]をご覧ください。[br][br]GeoGebraのアプリや試験での使用方法についてご質問がある場合は、遠慮なく [url=mailto:support@geogebra.org]support@geogebra.org[/url] までご連絡ください。
関数の定義
タスク
関数を定義し、グラフィックスビューにグラフを描き、関数の値やパラメータを指定します。
作図を確認
手順
[table][tr][td]1.[/td][td][i]入力バー [/i]に関数 [code]f(x)=x^3+6 x^2+6 x-4[/code] を入力し、Enterキーを押すと、新しい関数が定義されます。[/td][/tr][tr][td][/td][td][b][/b][b]注： [/b][i]y=f(x) [/i]のグラフは、自動的に[i]グラフィックスビュー[/i] に表示されます。[/td][/tr][tr][td]2.[/td][td][i]入力バー[/i] に [code]NSolve(f=0)[/code] と入力してEnterを押すと、方程式 [i]f(x)=0 [/i]の解を丸めた小数で出力されます。[br]注： [color=#0000ff]＝ [/color]トグルボタンを押すと、数値出力が正確な出力に変わります。数値出力の[img]https://wiki.geogebra.org/uploads/thumb/6/66/Numeric_toggle_button.png/24px-Numeric_toggle_button.png[/img]トグルボタンを押すと、再び，解を丸めた小数で表示します。[/td][/tr][tr][td]3.[/td][td]入力バー に [code]f({-5,0,2.15})[/code] と入力し、Enterキーを押して、x = -5、x = 0、x = 2.15の関数値を計算します。[/td][/tr][tr][td]4.[/td][td][i]入力バー[/i] に [code]Solve(f=4)[/code] と入力してEnterを押すと、方程式 [i]f(x)=4 [/i]の解が数値出力されます。[br][/td][/tr][/table][b]注：[/b]関数の値や方程式を計算した後、適切なトグルボタンを選択することで、[img]https://wiki.geogebra.org/uploads/thumb/6/66/Numeric_toggle_button.png/24px-Numeric_toggle_button.png[/img]数値と[img]https://wiki.geogebra.org/uploads/thumb/8/8b/Symbolic_toggle_button.png/24px-Symbolic_toggle_button.png[/img]記号の出力を切り替えることができます。
試してみましょう
タスク
関数族のグラフを描き、その関数値をテーブルビューで比較します。
手順
[table][tr][td]1. [/td][td]入力バーに [math]f\left(a,x\right)=\sqrt{x-a}[/math] [code]f(a,x)=sqrt(x-a)[/code] 入力し、パラメータ a に依存する関数族を定義します。[br][/td][/tr][tr][td]2. [/td][td]入力バーに [code]f(0,x) [/code]と入力し、Enter を押します。[/td][/tr][tr][td][/td][td][b][/b][b]注： [/b][i][code]y=f(0, x)[/code] [/i]のグラフが、自動的に[i]グラフィックスビュー[/i] に表示されます。[/td][/tr][tr][td]3.[/td][td]手順2を繰り返します。[code]f(1,x)[/code], [code]f(2,x)[/code], [code]f(-1,x)[/code] これらのグラフは[i]グラフィックスビュー[/i]に表示されます。[br][/td][/tr][tr][td]4.[/td][td]関数族のグラフを比較し、違いを確認します。[br][/td][/tr][tr][td]5.[/td][td] [code]f(0,x) [/code]の右側にある[img]https://wiki.geogebra.org/uploads/thumb/4/41/Icon-menu.svg/16px-Icon-menu.svg.png[/img][i]More [/i]ボタンをクリックして、[i]値の表[/i] を選択します。[/td][/tr][tr][td]6.[/td][td]ダイアログが開き、[i]xの開始値[/i]、[i]xの終了値[/i]、[i]ステップ [/i]を定義することができます。開始値を -1 に、終了値を 5 に、ステップを 1 と入力して、[i]OK [/i]を押して、設定を確定します。[/td][/tr][tr][td]7.[/td][td]手順5を f(1,x) でも [img]https://wiki.geogebra.org/uploads/thumb/4/41/Icon-menu.svg/16px-Icon-menu.svg.png[/img] [i]More[/i] ボタンを押して、[i]値の表 [/i]をもう一度選択します。[br][b]注：[/b]今度は、開始値と終了値を定義するダイアログは表示されません。これらの値は手順5ですでに設定されているからです。この値は後で変更することができます。[/td][/tr][tr][td][/td][td][b]注：[/b] [i]f(0, x)[/i] と [i]f(1, x)[/i] は自動的に [i]g(x)[/i] と[i] h(x) [/i]になります。[/td][/tr][tr][td]8. [/td][td][i]テーブルビュー [/i]で [code]f(0, x) [/code]と [code]f(1, x)[/code] の間数値を比較します。[/td][/tr][/table]
有理関数
タスク
与えられた関数 [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math] について [br][list=1][*][i]y=f(x) [/i]のグラフを描きます。[/*][*][i]f(x)=0[/i] の解と自然な定義域 [i]D[/i] を求めます。[/*][*][i]D [/i]の端における [i]f(x)[/i] の振る舞いを明らかにします。[/*][/list]
操作を確認
手順
[table][tr][td]1.[/td][td]入力バー に関数 [code]f(x)=(x^3+3 x^2)/(x^2+6 x+9)[/code] と入力し、Enterを押して [i]f(x)[/i] を定義します。[br][/td][/tr][tr][td][/td][td][b]注：[/b]GeoGebra 数式処理（CAS）は、[i]f(x)[/i] の方程式を自動的に簡単にします[/td][/tr][tr][td]2.[/td][td]コマンド [code]Root(f) [/code]で [i]f(x)=0[/i] の解を計算します。[br][/td][/tr][tr][td][/td][td][b]注：[/b]コマンド [code]Solve(f=0)[/code] を使っても解は計算できます。[/td][/tr][tr][td]3.[/td][td] f(x) の自然な定義域を求めるために、[i]f(x)[/i]の(分母)=0 の根を計算するコマンド Root(Denominator(f)) を入力します。[br][/td][/tr][tr][td][/td][td][b]注：[/b] コマンド [code]Solve(Denominator(f)=0)[/code] を使っても計算できます。[br][br][/td][/tr][tr][td]4.[/td][td]解が [i]-3[/i] なので，自然な定義域 は [math]D=\mathbb{R}\backslash\left\{-3\right\}[/math] （ [math]D=\{ x \in \mathbb{R} | x\neq -3\}[/math] ）[/td][/tr][/table]
試してみましょう
手順（続き）
[table][tr][td]5.[/td][td][i]Limit[/i]コマンドを使って、[i]D[/i]の端における[i]f(x)[/i]の振る舞いを確認しましょう。[/td][/tr][tr][td][/td][td][i]入力バー[/i] にコマンド [code]Limit(f,-infinity)[/code] を入力して、左端の振る舞いを確認します。[/td][/tr][tr][td][/td][td][i]入力バー[/i] にコマンド [code]Limit(f,infinity)[/code] を入力して、右端の振る舞いを確認します。[/td][/tr][tr][td]6.[/td][td]コマンド [i]LimitBelow[/i] と [i]LimitAbove[/i] をつかって -3 の近傍の振る舞いを確認しましよう。[br][/td][/tr][tr][td][/td][td][i]入力バー[/i] にコマンド [code]Limitbelow(f,-3)[/code] を入力します。[/td][/tr][tr][td][/td][td][i]入力バー[/i] にコマンド [code]LimitAbove(f,-3)[/code] を入力します。[/td][/tr][tr][td][/td][td][br][/td][/tr][/table]