IM Geo.4.11 Lesson: Approximating Pi
Calculate the area of the shaded regions.
Calculate the area of the shaded regions.
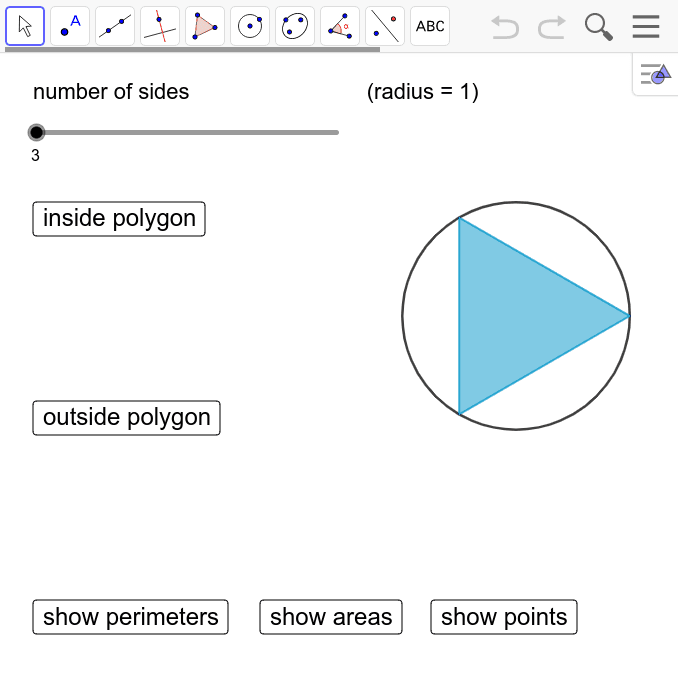
The applet below shows a regular n-sided polygon inscribed in a circle.
Come up with a general formula for the perimeter of the polygon in terms of [math]n[/math]. Explain or show your reasoning.
Let's use the expression you came up with to approximate the value of π.
How close is the approximation when [math]n=6[/math]?[br]
How close is the approximation when [math]n=10[/math]?[br]
How close is the approximation when [math]n=20[/math]?[br]
How close is the approximation when [math]n=50[/math]?[br]
What value of [math]n[/math] approximates the value of [math]\pi[/math] to the thousandths place?
Describe how to find the area of a regular [math]n[/math]-gon with side length [math]s[/math]. Then write an expression that will give the area.
IM Geo.4.11 Practice: Approximating Pi
A regular pentagon has side length 7 inches.
What is the perimeter of the pentagon? [br]
What is the area of the pentagon? [br]
[size=150]The expression [math]n\cdot sin\left(\frac{360}{2h}\right)[/math] approximates [math]\pi[/math] by giving the perimeter of a regular polygon inscribed in a circle with radius 1.[br][/size][br]What does [math]n[/math] stand for in the expression? [br]
If there are 60 sides, what is the difference between the perimeter and [math]\pi[/math]? [br]
Technology required. A regular hexagon has side length 2 inches.
What is the perimeter of the hexagon? [br]
What is the area of the hexagon? [br]
An airplane travels 125 miles horizontally during a decrease of 9 miles vertically.
What is the angle of descent?[br]
What is the distance of the plane’s path?[br]
Select [b]all [/b]true statements.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMUAAAGYCAYAAADyXyZtAAAgAElEQVR4Ae2dd6wVRRvGEbGgIqjY0XvFruDFLjYEFQsqKFKsIFgQC9gQbIBdEEFN7AjWxBiDBbBG1CigqCTqH/ZrjUZF7GhiMl/ekTnfnj3vnrNlZnZm95nk5J6dMzvl985zZstz97QRSCAAAlUE2lRtYQMEQEBAFJgEIBAiAFGEgGATBCAKzAEQCBGAKEJAsGmPQGtrq5g0aZIYO3asOOigg+TfGTNmCMrPM0EUedIvadvLly8Xw4cPF23atIl85SkMiKKkEzOvYS9dulT06NFDiqFXr15izpw5gkRCif7OmjVLTJ8+Pa/uyXYhilzxl6txmvTNzc1SEMOGDXN28BCFs6EpXsfGjBnjvCCIOkRRvLnn5IjoHIHOITp27Fg5XHKyoxCFq2EpXr/oPIFEQauF6wkrhesRKkj/mpqapCjoRNv1BFG4HqGC9E9dfvVhOBCFD1HyvI+0OpAoWlpavBgJROFFmPzu5IIFC6Qo6L6EDwmi8CFKnvdRiYJu2vmQIAofouR5H+mmnTqnUHevXR4SROFydArUNzqfIGFMnDjR+VFBFM6HqBgdJI+TWi3ICRtOdDLuyioCUYSjg21jBMjsp4TRqVMnaRdX5kDKp3MPFxJE4UIUStQHWhHIDEhXosjyQX/pRYdVWClKNBEwVL8IYKXwK17orQUCEIUFyGjCLwIQhV/xKkxvly1bJj799FMnxwNROBmW4naKTrQPP/zwylWoLl26iGnTpjk1YIjCqXAUuzM//PCD2GSTTSqCUJdn6e+UKVOcGTxE4Uwoit+RyZMns4IgUWy44YbOAIAonAlF8TvSt2/fSFGQMN577z0nIEAUToShHJ0YPHhwXVF88cUXToCAKJwIQzk6MXv27EhR7LPPPs5AgCicCUU5OnL88cfXCGONNdYQL7/8sjMAIApnQlGOjtx5551SFOuss478SyL56KOPnBo8ROFUOIrfma233lqKgR6oTCfXrjhjg+QhiiANvDdKYOHChVIIJAaIwihqVO4LgeOOO06KYsSIERCFL0FDP80R+OOPPyqrxOuvvw5RmEONmn0hQD/OQodN++23n+wyDp98iRz6aYyAuto0c+ZMiMIYZVTsDQH10ILOnTtX+oyVooICb8pIgA6Z6NBp3LhxleFDFBUUeFM2Ap999lnlBPvDDz+sDB+iqKDAm7IROPvss6Uo+vfvXzV0iKIKBzbKRIAOm+j11FNPVQ0boqjCgY2yELjrrrukIHbYYYeaIUMUNUiQUQYC22yzjRQF96+mEEUZZgDGWEVg0aJFUhB06PTTTz9VfUYbEEUNEmQUncDAgQOlKMjnxCWIgqOCvMIS+PPPPyurxBtvvMGOE6JgsSCzqATUUzuUz4kbJ0TBUUFeYQl06NBBrhTK58QNFKLgqCCvkASefPJJKYigz4kbKETBUUFeIQnsv//+UhRBnxM3UIiCo4K8whH4/PPPKyfYQZ8TN1CIgqOCvMIRGD16tBRF2OfEDRSi4Kggr3AEonxO3EAhCo4K8gpF4O6775arBOdz4gYKUXBUkFcoAttuu60UBedz4gYKUXBUkFcYAosXL5aCWGWVVVifEzdQiIKjgrzCEFDPhx05cmTsMUEUsVGhoG8E4vicuDFBFBwV5BWCwNVXXy0Pnfbdd99E44EoEuFCYZ8IrL322lIUXbt2FVdccYV46aWXxN9//91wCBBFQ0Qo4CMB+r9rujdBv1e3fPly8fjjj4tzzz1X7LHHHmLUqFGCHrv/6quvim+//bZmeBBFDRJkFIHAAQccIEVx6aWXVg1nxYoVgp4Xe8cdd4jzzz9f9OvXT/Ts2VMMGDBA0Mn4mDFjxJZbbin3xaP4q9Bhw2cCra2tclLTShHnR1fokIp+045+R/u1114TLS0tEIXPEwB9ryVAh0kkiDg+p9q98T/aHBPkeU4gic+JGyrOKTgqyPOWwD333CNXiSifEx0iTZw4Ub7o4cpcgig4KsjzlsB2220nRcH5nGbNmiUPqehqFKVevXoJOv8IJ4giTATb3hJ48803pSA4nxNdSerYsaO8PKsGSCsGXW0KJ4giTATb3hIYNGiQFEXY50QrQ3Nzs6CVIphIFLRahBNEESaCbS8J1PM50eRvamqqGRfld+rUqSYfoqhBggwfCVxzzTVylaCHEwQTrRI08bnDpGHDhsl9guXpPUQRJoJtLwnQ+QJdir3//vur+j99+nSZT1edwolu0uHwKUwF24Ug8PTTT8uJTz6ncKKJT4IJJ1pBom7wYaUI08K2dwQOPPBAOcHDPidl96CTbPpZ4OBr+PDhch86rwgniCJMBNteESDPkrqDHfY5qV8+pUOocKJzDNqPO6yCKMK0sO0VgfPOO09ObnK5hhOtAlETnw6ruCtSVAdEESaJba8IqFWCzivCSa0G4Xx1WMUdOlFZiCJMDNveELj33nvlSrDjjjuyfaYrS9xqQIdT4bvbwQogiiANvPeKwPbbby9FMXXqVLbfdB+Cu+RKQolaJagiiILFiUzXCbz11ltSEORzWrZsGdtdmvhhUdAqQaJQpkBuR4iCo4I85wkMHjxYiuL000+P7CudOwQPn9Q2d8UpWAlEEaSB914QCPqcFi5cWLfPdLI9Y8YMQT/YQodTjQRBlUEUdZHiQxcJXHvttXKVCPucovpKQogjBrU/RKFI4K83BMjgR5diwz4nXQOAKHSRRD1WCDzzzDNSEJzPSVcHIApdJFGPFQJ0NYlWibDPSWfjEIVOmqjLKIF6PiedDUMUOmmiLqME6Il+tEpwPiedDUMUOmmiLqME6vmcdDYMUeikibqMEbjvvvvkKhHlc9LZMEShkybqMkaAHm5GK0WUz0lnwxCFTpqoywiBJUuWSEG0bds20ueks2GIQidN1GWEwJAhQ6Qo6vmcdDYMUeikibq0E0jic9LVOEShiyTqMULguuuuk6sE/QiLrQRR2CKNdlIRWG+99aQowo+8TFVZzJ0gipigUMw+gblz50pBbLTRRlYbhyis4kZjSQioyTl+/Pgku2Uuq9rFb95lRokKdBII+pw+/vhjnVU3rAuiaIgIBfIgoB5PY9rnxI0NouCoIC93AsrnRP8/YTtBFLaJo72GBGbOnClPsG34nLjOQBQcFeTlSoDEYMvnxA0UouCoIC83ArZ9TtxAIQqOCvJyIzB06FC5StjyOXEDhSg4KsjLhcBff/0lBUGHTo2e52SygxCFSbqoOxGB66+/XorCps+J6yBEwVFBXi4E1l9/fSkKmz4nbqAQBUcFedYJzJs3TwrCts+JGyhEwVFBnnUCvXv3lqKw7XPiBgpRcFSQZ5VAnj4nbqAQBUcFeVYJjB07Vq4Sxx57rNV2oxqDKKLIIN8agTx9TtwgIQqOCvKsEaAnh5ModtppJ2ttNmoIomhECJ8bJUBiIFHcfPPNRttJUjlEkYQWymolEPQ5/fzzz1rrzlIZRJGFHvbNROCEE06Qq8QZZ5yRqR7dO0MUuomivlgEgj6nRYsWxdrHViGIwhZptFNF4IYbbpCrRN4+p6pOrdyAKDgqyDNOYIMNNpCiyNvnxA0UouCoIM8ogfnz50tBuOBz4gYKUXBUkGeUQJ8+faQoXPA5cQOFKDgqyDNG4Msvv5SCoHsTtp/nFHdQEEVcUiinhcAFF1wgReGKz4kbFETBUUGeMQKu+Zy4gUIUHBXkGSFAV5pc8zlxA4UoOCrIM0Jg5513lqJwyefEDRSi4KggTzsB5XNaddVVhUs+J26gEAVHBXnaCZx44olylXDN58QNFKLgqCBPKwGXfU7cQCEKjgrytBK48cYb5Spx4IEHaq3XVGUQhSmyqLdCoHPnzlIUs2fPruS5/AaicDk6Beib8jltvPHG3owGovAmVH529OCDD5arxIQJE7wZAEThTaj862jQ5/TJJ594MwCIwptQ+dfRCy+8UK4SLvucOKoQBUcFeVoIKJ8T/R62Twmi8ClaHvWVrjT54HPikEIUHBXkZSbQrVs3KQrXfU7cQCEKjgryMhF4++23pSB88DlxA4UoOCrIy0TgpJNOkqLwwefEDRSi4KggLzUB33xO3EAhCo4K8lITuOmmm+Qq4YvPiRsoRMFRQV5qAhtuuKEUhS8+J26gEAVHBXmpCPjoc+IGClFwVJCXisAhhxwiVwmffE7cQCEKjgryEhPw1efEDRSi4KggLzGBiy66SK4Sxx13XOJ9XdsBonAtIp72x1efE4cbouCoIC8RgQceeECuEvQImyIkiKIIUcx5DN27d5eimDZtWs490dM8RKGHY2lrUT6ndu3aieXLlxeCA0RRiDDmN4iTTz5ZrhJnnnlmfp3Q3DJEoRlomaoL+pwWL15cmKFDFIUJpf2BTJkyRa4SPvucOGoQBUcFebEI0M9z0aVYn31O3EAhCo4K8hoSePbZZ6UgfHqeU8NBrSwAUcQlhXJVBA499FApCt99TlWDWrkBUXBUkFeXQJF8TtxAIQqOCvLqErj44ovlKlEEnxM3UIiCo4K8ugSK5HPiBgpRcFSQF0mgaD4nbqAQBUcFeZEEdtllF3noVBSfEzdQiIKjgjyWQBF9TtxAIQqOCvJYAqeccopcJYrkc+IGClFwVJBXQ2DFihVSEHSSXSSfU81AhRAQBUcFeTUEpk6dKkXRq1evms+KlgFRFC2ihsZDdg5aJejqU9ETRFH0CGsYn/I5bbLJJhpqc78KiML9GOXew759+8pV4rLLLsu9LzY6AFHYoOxxG0Gf06effurxSOJ3HaKIz6qUJS+55BK5SgwcOLA044coShPqdANdZZVVpCjmzZuXrgIP94IoPAyarS4/+OCDUhBFeZ5TXG42RdHa2ipeeeUV+YrTvzZxCqGMOQItLS1SFEX2OXH0sohizJgxklmj+zmzZs0SPXr0kGWV65j+DhgwQJBQohJEEUXGQn7Q5/TLL79YaNGdJtKIgp55pfajyV1PFP3795diaGpqEhMnThQLFiwQJBKV36lTp8hnaEEUOc6TU089VQau6D4nDrGa3DRZ4yQqRxO5Y8eOcnI3EsXSpUulGLi61UpDf7kEUXBULOSVyefE4UwqCvrGJ0HQZKfUSBRcmyqPBFZvf4hCkbL8l377ul5gLHfHenNJRUFiCD4yNAs7Op+otz9EYX06/Ncg2TkoMGXwOXGIk4oiXEe9SR0uG96eM2eOZI/DpzCZHLfL5nPiUOcpCjpBJ1GpQ7Fw/7BShIlY2D7ssMNkUMric+KQ5iUKugJFgqCrUFEJoogiYyj/q6++kkGhwJTF58ShzEMUtDLQFSy6NxQ8Pwn3D6IIEzG8PW7cOCmKMvmcOKS2RaEEEbyCxfWL8iCKKDKG8tu2bStFUSafE4fSpiiSCAKi4KJlME/5nLp162awFT+qtiWKpIIgelgpLM4h5cO55ZZbLLbqZlM2RJFGEBCFxfmifE6rrbaaKJvPicNsWhRpBQFRcNEylDds2DB5LnHWWWcZasGvak2Kgu5Y01UmusJHjthJkyZFvjjvFQ6fLMyloM/pzTfftNCi+02YFIXyNpEoGr3IQRtOEEWYiIFt+l8JCk49q7OBZp2uMqsoaOLTIRKX6B4EfR7nxf1fBUTBUdWct+mmm0pR0NUnpP8IZBWFSY4QhUm6Qgj4nHjAEAXPpRS5hx9+uFwlyuxz4gINUXBUSpAHn1N0kCGKaDaF/uTSSy+Vq0TZfU5ckCEKjkoJ8lZddVUpirL7nLhQQxQclYLnwedUP8AQRX0+hfx01113lasEfE58eCEKnkthc9955x0pCPicokMMUUSzKeQnw4cPl6KAzyk6vBBFNJvCfQKfU7yQQhTxOBWilPI5UdCRoglAFNFsCvfJ5ptvLg+d4HOqH1qIoj6fwnyqfE5kAESqTwCiqM+nMJ8eccQRcpW4/PLLCzMmUwOBKEyRdajeoM/ps88+c6hnbnYFonAzLlp7NX78eLlKHH/88VrrLWplEEVRIxsYV7t27aQo5s+fH8jF2ygCEEUUmYLkw+eUPJAQRXJmXu2x2267yVUCPqf4YYMo4rPyrmTQ5/Trr7961/+8OgxR5EXeQrunnXaaXCXgc0oGG6JIxsub0vA5pQ8VRJGendN7wueUPjwQRXp2Tu/ZpUsXeegEn1PyMEEUyZk5v8dzzz0nBQGfU7pQQRTpuDm915FHHilFAZ9TujBBFOm4ObsXfE7ZQwNRZGfoVA3wOWUPB0SRnaFTNdADCegp4vA5pQ8LRJGenXN7Kp9T9+7dneubTx2CKHyKVoO+7r777nKVmD59eoOS+LgeAYiiHh2PPlM+p9VXX13A55QtcBBFNn7O7D1ixAi5SowaNcqZPvnaEYjC18gF+h30Ob311luBT/A2DQGIIg01x/aBz0lvQCAKvTxzqW2LLbaQh04PPfRQLu0XrVGIwvOIwuekP4AQhX6mVmvs16+fXCXgc9KHHaLQx9J6TUGf0+eff269/aI2CFF4HFn4nMwED6Iww9VKrXSjDj4n/aghCv1MrdRIV5pIEPA56ccNUehnaqXGPfbYQ4oCPif9uCEK/UyN1wifk1nEEIVZvkZqHzlypFwl4HMygldAFGa4Gqv177//loKg8wn4nMxghijMcDVWq/I59e7d21gbZa8YovBsBmy55ZZypYDPyVzgIApzbLXXrHxOm222mfa6UeH/CUAU/2fh/LujjjpKrhJXXHGF8331uYMQhSfRg8/JXqAgCnusM7WkfE6DBg3KVA92bkwAomjMyIkSa6yxhjx0ot/DRjJLAKIwy1dL7fA5acEYuxKIIjaq/AruueeecpWYMWNGfp0oUcsQhePBDvqcfvvtN8d7W4zuQRSOxxE+J/sBgijsM4/dInxOsVFpLQhRaMWptzL67Wsy/sHnpJdro9ogikaEcvy8qalJigI+J7tBgCjs8o7dGnxOsVFpLwhRaEeqp8Kjjz5arhLwOenhmaQWiCIJLUtlv/76aykIOp/A85wsQQ80A1EEYLjyFj6nfCMBUeTLn219zTXXlCsFfE4sHuOZEIVxxMkaUD6nXXbZJdmOKK2NAEShDaWeivbaay+5SsDnpIdnmlogijTUDO2jfE5kE4fPyRDkGNVCFDEg2SqifE5nn322rSbRDkMAomCg5JEV9DktWbIkjy6gzZUEIApHpoLyOfXp08eRHpW3GxCFI7Fvbm6WJ9gPP/ywIz0qbzcgCgdiD5+TA0EIdAGiCMDI6+0xxxwjVwn4nPKKQHW7EEU1D+tbQZ9Ta2ur9fbRYC0BiKKWidWcCRMmyFUCz3Oyir1uYxBFXTzmP2zfvr0UBXxO5lnHbQGiiEvKQDn4nAxA1VAlRKEBYtoq9t57b7lKwOeUlqCZ/SAKM1wb1vruu+9KQcDn1BCV9QIQhXXk/zUIn1NO4GM0C1HEgKS7CHxOuonqrQ+i0MszVm3wOcXClFshiCIH9FtttZU8n4DPKQf4MZqEKGJA0llE+Zw233xzndWiLo0EIAqNMONUpXxOV155ZZziKJMDAYjCInT4nCzCztAURJEBXtJdlc9p8ODBSXdFeYsEIAqLsNdaay15gk3nFUjuEoAoLMUGPidLoDU0A1FogBinin322UeuErfeemuc4iiTIwGIwgL8oM/p999/t9AimshCAKLIQi/mvqeffrpcJfA8p5jAci4GURgOAHxOhgEbqB6iMAA1WCV8TkEafryHKAzHqWvXrvA5GWasu3qIQjfRQH3PP/+8FAR8TgEoHryFKAwGCT4ng3ANVg1RGIILn5MhsBaqhSgMQYbPyRBYC9VCFIYgr7322vJ8Aj4nQ4ANVgtRGICrfE4tLS0GakeVpglAFAYI9+zZU64S8DkZgGuhSohCM2Tlc6Kf/YXPSTNcS9VBFJpBK5/T6NGjNdeM6mwRgCg0kv7nn3/kYVObNm3E22+/rbFmVGWTAEShkbbyOR188MEaa0VVtglAFBqJb7311nKleOSRRzTWiqpsE4AoNBGHz0kTSAeqgSg0BaF///5ylcDznDQBzbEaiEID/KDP6YsvvtBQI6rIkwBEoYE+fE4aIDpUBUShIRjrrLOOPHSCz0kDTAeqgCgyBoGeHE73JeBzygjSod0hiozBgM8pI0AHd4coMgQFPqcM8BzeFaLIEBz4nDLAc3hXiCJlcOBzSgnOg90gipRBmj59ujzBhs8pJUCHd4MoUgZnm222kaKAzyklQId3gyhSBEf5nLp06ZJib+ziOgGIIkWElM/pqquuSrE3dnGdAESRMELffPONPGyiG3bwOSWE50lxiCJhoJTPaciQIQn3RHFfCEAUCSPVoUMHuVLQeQVSMQlAFAniCp9TAlgeF4UoEgRv3333lavEbbfdlmAvFPWNAEQRM2JBn9Mff/wRcy8U85EARBEzavA5xQRVgGIQRYwgBn1O77zzTow9UMRnAhBFjOjB5xQDUoGKQBQxggmfUwxIBSoCUTQIJnxODQAV8GOIokFQ4XNqAKiAH0MUdYIKn1MdOAX+CKKoE9zLLrtM3qyDz6kOpAJ+BFHUCeq6664Ln1MdPkX9CKKIiKzyOfXo0SOiBLKLSgCiiIgsfE4RYEqQDVEwQV66dKk8bGrfvr2Az4kBVPAsiIIJsPI5nXPOOcynyCo6AYgiFGH4nEJASrgJUYSCrnxOhxxySOgTbJaFAEQRivS2224rzyceffTR0CfYLAsBiCIQaficAjBK/BaiCARf+ZwmTpwYyMXbshGAKFZGPOhz+vLLL8s2DzDeAAGIYiUM+JwCs6LkbyGKlROgY8eO8DmVXAxq+BCFEAI+JzUd8JcIQBRCCB0+pzlz5ohJkyYJus/x5JNPYnZ5TKD0osjqc6L9e/XqJcWg5sGsWbMEXckKpgULFgQ38d5hAqUXxRlnnCHPJehv0kSC6NSpk6BVIpyampoEiUOlYcOGqbf46ziBUosi6HPq3r27uPXWW8Uvv/wSK2TLly8Xzc3NImqy00pBKwil1tbWqpUkVgMolBuBUosi6HP67rvvxJQpU8QBBxwgT7wbRYRu8NFvVNBqwSX1OX1G70lESH4QKLUoOJ/Txx9/LMaOHSvOPPNMQe+jEh0e0SsqKVHQKkHvkfwhUFpRvPDCC/KbfosttmCj9dhjj4k999xTPPXUU+zntEqET6aDBZUoxowZE8zGew8IlFYUcXxO77//vhg4cKC48847a0JJoqi3AihRRB1e1VSIDGcIlFIUSXxOdC5w1llnialTp1YFje6A1xMFnYCTcJD8I1BKUSif09ChQ2NF7N9//xXnnnuumDZtWqU8XW7lnvShziHUSqFOsLnLtpXK8MYpAqUUBd1boG9xOq+Im+jy7YgRI8T9999f2YWuXtGKMHv2bDFjxgy5cpBYlBDoEI1O2um8gsSC5AeB0olC+Zx23XXXxBH6/vvvxZFHHileeumlqn2VCKoyV27U+4wrj7z0BBYuXCjvDfXu3VtkeakvTRddCEYOyJXP6fbbb09Ff/HixaJPnz6CBILkFgESBV1K//XXXzO96F4VHUmUQhR0JYgGS89z+vPPP1NH9J577hHjxo1LvT92NEOAREHnfllTqQ6flM9Jx/OcTj31VDF//vys/LG/RgIQRUKYQZ8T/dJp1kSHUfVu3mWtH/snJwBRJGQW9Dkl3DWy+Pjx42P5pCIrwAdaCUAUCXFyPqeEVdQU/+CDD0S/fv1q8pGRDwGIIgH3Rj6nBFXVFD3//PPF3Llza/KRYZ8ARJGA+YABA+RVp3q2jATVVRV98cUXxejRo6vysJEPAYgiJvckPqeYVdYUo0t4uG9Rg8V6BkQRE3lSn1PMaquKXXnlleKJJ56oysOGfQIQRUzm6pZ9Ep9TzKorxeicgq5EIeVLAKKIwf+RRx6R5xJpfE4xqq8U+frrr6UnqpKBN7kQgChiYM/qc4rRRKUI+aGWLVtW2cYb+wQgigjm5Gmi/12YPHmyXCXWWmutTD6niGZqsslWruNOeU3FyIhNQIcoVqxYIbp16ybnzsyZM2O3batgYpfsfffdJzp06CAHRMY/em2//fZW+nv55ZfDC2WFdHQjWUVB/wujnims5s8JJ5wQ3WAOnyQSBXmR1EDCf3U4JxuN/+abbxZ0DoOUH4EsoliyZEnk/Bk1alR+gwq1nEgUdAMtLAa13bZtW0GXTelZr6ZeRx11lDjmmGOM1W+q30Wqd+TIkWKvvfZKFYO99947cv7QPMryrwaheZ1pM5Eo9ttvv7qDUgLB3/8OK8EhGQdaSVxIiUQxfPjwuqKYMGFCqm+QIn2TYizRRwq77bZb3fnz008/uaAJkUgU9A8/Ud9+rp0sOUEXnagioEyj3BwaNGhQVdk8NxKJgjqqHisTHNj+++8vfvzxxzzHgbY9IXD11VfXfLH27NlT0HOGXUmJRUEdf++99+SDksl2gWctuRJKf/pBT4WkB23T/HHRz5ZKFP7gR09BIDkBiCI5M+xRcAIQRcEDjOElJ5BZFHROQZch8eTv5PDLuAc92jR82ZoeifrKK69UHoWaN5dMoqABqqtQJv4NNW84SdsnX0844MFtPOtWyJ9gU3Mm/Jf+L4eeCJN3yiQK9Sh8Ghx+OEXUGN3CQXfxEZG2J6CaMzT5iYd6BS/1531FM7Uo1OMx1SDVDzLahuxSeySClpaWSqBVwNVfPAhaSD7EiWOhhJH3F2xqUZAIaHDqEIr7HQmXJqyNvhAPPNGwPmliFPU7hvTl4QLDVKJQnadVgpISSH0cxf5UrZw4t4qOc3jehEvSCkGiyPu8IpUo6BCBOq9OHJUouCUxPPCibquAQxTREVaHR9ykJ350ok3/gJT3PEosCrrCQoIIHvcphdPAypqUKCjgtGrQJUaXLjO6EBc6tKS5Q25rdVWOfoWKDr0pn75cXbi0n1gUdDwYVrP6Bsj7qkGegVdfFhTc8IuCXuYvDBUXmjthNmqbRJL3CqH6mUgUavLTIzLVNyH9pQHR4Mp86EABpVC9PHgAAAGPSURBVFWCGNCXA4mA3qtvR+JDwilrUhdkaDUIJuKkjjRcuVgTWxQUdPXQM6Xu8N/gIVVw4GV/TyIhVsSvrEkxiJoj6tI+d75hm1lsUahVgr756H34RUEPfwvYHozL7amLEWU9jFLzJ2q1VIef6opmnrGMJQq19EVdX6YBkCiam5vzHIvTbatJUVZRqC8FdcUyHCzFJ2olCZc3uR1LFGppi1I5dVCdRJnsrM91q3OLsoqCLs7Qi0t0aK6uQNWbY9y+JvIaikLdlKq3SlDHGn0TmOi8L3UGz8fofdmSmkPc4TV9SahfSqX7Xy6khqJQk72RgtVqUtZvQnV/IhxUmhDqW5AOEcqY1PlC+MJMcJtWUle+MOqKgo7/SBRxTn5o4FS2rKJQXx4UaPrmoxedY6nAu3CsnJcg1dwgRsGXumjjwg27IJu6oggWxPv6BOgLhFaCYNDpPYnBtaDXHwk+hSgwB0AgRACiCAHBJghAFJgDIBAiAFGEgGATBCAKzAEQCBGAKEJAsAkCEAXmAAiECPwPHCunYE7rMUMAAAAASUVORK5CYII=[/img]
Write 2 equations using sine and 2 equations using cosine based on triangle [math]ABC[/math]. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAATYAAADBCAYAAABFXJy8AAAdSklEQVR4Ae2dCfQN5R/GKS2UJVEq+ilKWSLRIkLRImVJpRASHY4tIaQQKpF2nBZb0aFDKgohVOioQ8dSOqJoT0mFE+X7P8/Ud/5z729m7sy9M3O35z3nnrl35l0/73ufefe3iNCQAAmQQI4RKJJj6WFySIAESEAobCwEJEACOUeAwpZzWcoEkQAJUNhYBkiABHKOAIUt57KUCSIBEqCwsQyQAAlkFIEiRYpI/KdMmTLSunVree+99zzFlcLmCRMtkQAJREFgw4YNhqgVFBTIiBEjjE/nzp2ldu3apthNmzYtYVQobAkR0QIJkEBUBCBaqK1B1OKNPqtTp078o0K/KWyFkPAGCZBAugj069fPELbXX3/dNgraRLV9aLlJYbPA4FcSIIH0EtAm5969e20jAmErXbq07TPrTQqblQa/kwAJpJUAhAv9a3bmiSeeMGpzqNUlMhS2RIT4nARIIBICGPGEsLVq1coMD4MJK1eulC5duhjPGjduLE61OdORCJdUWWHwOwmQQPoIaI1M+9GsVwiaU7+bXYxZY7OjwnskQAKRE0BNDWKG6R061QNXiBruN2nSxFNtDRGnsEWefQyQBEjAjgD61iBgdgYCp6Jn9zz+nr0v8bb4mwRIgARCJIB+MwgXRkXtjD53Er54NxS2eCL8TQIkEDkBHThwG/GEqFHYIs8aBkgCJJAsAW1qOi2XwsCBW40uPlzW2OKJ8DcJkEDkBHSAANM74s3OnTulcuXKhrBh5NSLobB5oUQ7JEACoRLAagLUyEaOHBnzwUioNkExWurVUNi8kqI9EiCBUAigRqbiZXfFNBA/c9gQSQpbKFlFT0mABNJJgMKWTvoMmwRIIBQCFLZQsNJTEiCBdBKgsKWTPsMmARIIhQCFLRSs9JQE8pvApk2bpG/fvnLJJZdImzZtZObMmZECobBFipuBkUDuE1i4cKHtKGfXrl0jSzyFLTLUDIgE8oNA9erVbYUNUzn8TttIlhiFLVlydEcCJFCIwMaNGx1FDcLWvXv3Qm7CuEFhC4Mq/SSBPCWwatUqV2G7+eabIyFDYYsEMwMhgdwnMGfOHKlWrZqrsHld65kqLQpbqgTpngTynMD8+fOlZs2apqCVLFnS/G5dIlW1alU5cOBAJLQobJFgZiAkkHsE3nzzTcHhxSpe5cuXlylTphgJHTNmjJQpU8Z8duONN8q2bdsig0Bhiww1AyKB3CDw9ttvS/369U3RgoA988wzhRKnm0c2bNiw0LOwb1DYwiZM/0kgRwgsXbpULrvsMlPQTjzxRHHrM1Nhw9ZDURsKW9TEGR4JZBkBCFSjRo1MQTv++OPlscceS5gKCltCRLRAAiQQNYH3339fmjZtagpasWLFZOzYsZ6jQWHzjIoWSYAEwiawdu1aad68uSloGBwYNWqU72ApbL6R0QEJkEDQBNavXy8tWrSIEbThw4cnHQyFLWl0dEgCJJAqASyDwnQMnbaB63333SeHDh1KyWsKW0r46JgESCAZAps3b5a2bdvGCNq9994b2CRaClsyuUI3JEACSRH4/PPP5ZZbbokRNOydtm/fvqT8c3JEYXMiw/skQAKBEdi+fbt06NAhRtCwCeSePXsCC8PqEYXNSoPfSYAEAiXw9ddfC87ktPah3XXXXTJr1iwJc/NHClug2UjPSIAEQODbb7+Vbt26xQhaly5dZPfu3Sagfv36hbZtN4XNxMwvJEACqRL48ccf5e67744RNDRBd+zYUchr3Lv44otl69athZ6leoPClipBuicBEpBffvlFevfuHSNoGCRItKvGvHnzpGPHjnL48OFAKVLYAsVJz0ggvwhgNLN///4xgoZpHFu2bPEMAms/hwwZ4tm+F4sUNi+UaIcESCCGADZtHDhwYIyg3XDDDYIJt8mYQYMGycMPP5yMU1s3FDZbLLxJAiRgRwArAlC7Klq0qClq1157rWBJVKoGgwl+Frq7hUdhc6PDZyRAAgaBI0eOyAMPPCDHHHOMKWjNmjUTLFoP0mA5FWpvqW7jTWELMlfoFwnkIAHsrlG8eHFT0Bo3biyrV68OLaXYQBIDDxs2bEg6DApb0ujokARymwCahdipVifXNmjQQJYvXx5JonGiOzaYfP7555MKj8KWFDY6IoHcJTBu3LiYw1Aw12zJkiWRJ/i7774z+vPat2/vW1ApbJFnFwMkgcwkMHHiRClXrpxZQ7vwwgsFNad0G4hUp06djJPc3333XU/RobB5wkRLJJC7BJ5++mmpUKGCKWi1atWS119/PeMSjFpj9+7djf3bnnvuOdcVCxS2jMs+RogEoiEwadIkqVixoilo1atXl9deey2awFMIBUuwnnrqKbnpppuMXXfvv/9+eeWVV2TNmjWCRfd//vmnUNhSAEynJJCNBNAhX1BQYAraueeeK7Nnz87GpBhChsOTx48fL7169ZLWrVsbgw7VqlUz0sfj97IyWxlpEvBOYOrUqVKlShVT0M4++2yZMWOGdw+yyOaKFSsobFmUX4wqCfgm8PLLL4vWYDB148wzz5QXX3zRtz/Z5IBN0WzKLcaVBHwQePXVV6VGjRpmDe2MM86QKVOm+PAhe61S2LI37xhzErAlgAGACy64wBS0U089VZ555hlbu7l6k8KWqznLdOUdAUzRqFu3riloJ598smBuWj4aCls+5jrTnFMEMIkWqwN06VOZMmUEe5zls6Gw5XPuM+1ZTWDx4sWC9ZsqaFjXGdS2P17AoIaIcwwwpUI/06ZNc3Xq1c3evXtlwYIFxmfnzp2ufto9pLDZUeE9EshgAsuWLTPmaqmgHX/88TJy5MjIYgzRgZBp+NjtQz/YmcPOWN2ULl3atA938W6wq0ft2rWN+xDKVq1aSSLBjA+TwhZPhL9JIEMJrFy5Upo2bWoKCvZGGz58eKSxhUDVqVPHiMOIESMEvxOZeDeJ7EPU4v2FAMbfc/OHwuZGh89IIAMIfPjhh9K8eXNT0LB7LTZkxG62URvscouaWnwtyy0eftyg2Qn78QYiCrHyaihsXknRHglETOCjjz6S6667zhQ0CMqAAQNk//79Ecfk3+BQY8LABJZjeTVwg3h7dQP7OGA53lDY4onwd9YQQN+KdkInuvrtc8kaCCLyySefCA5G0T4sXPv27Ss4ESqdBh3/iAtExqtBPvl1g2andfdc1OJwz49hjc0PLdoNlYAWRusf2um7nz9XqJEO0PNPP/3UWMRtTXPPnj1lz549AYaSvFdgjrhpkxBCh0ELfKZPn27bB+bmBqOedv1muIcBAyxoxyde6LykQMsSXpBRmyJRB8jwsp8ACjz+XMlMAcjU1GMbnnbt2hnpUlG766675Pvvv8+oKENgED/UwnQAQeOLK5qp1poWIq9uIIKVK1eOSaOTG2ui7YTP+tzpO4XNiQzvZxwBiBn+DH6bJRmXkP8i9MUXXwi2vbaKA+aF7d69OyOjrCIFgUIHv/XlgsEETOOAuFnFKJEbFTermyAST2ELgiL9iIQAOpXxR9CmUCSBhhDIjh07pGPHjjGC1qFDB8H9TDYqUnajloi3NjutI6bqxqnrwM5NEAwobEFQpB+hE9DaGuY4ZavZtWuXdO3aNUbQbr31Vtm2bVtWJElFKr65qZFXMYE9NerGWrvTZ7iqG3QxBGnUX/axBUmVfgVOQN/s2Tgair4y7NVvbXJiW+vNmzcHzilMDxP1b6I5iTRahU3dODU1IZLxboJIA4UtCIr0I1QC+FP4nT8VaoQ8ev7zzz8LRjWtgoY/+saNGz36kFnW0MREWpxeLiom1tqXusHggZ1RN3Zz1+zse72n/rLG5pUY7UVOQGtrTv00kUcoQYAQ4j59+kixYsVMUWvZsqWsX78+gcvMfqzdAU5iYbfCIJEb7Td1EstkiVDYkiVHd5ERwKx1jLg5NWcii0iCgP744w9jZQAWpWst7dprrzVOT0rgNGseq3hh9NaaH1ozs8unRG68rkrwA4nC5ocW7UZOAG9yiITTSFzkEbIJ8ODBgzJ48GA54YQTTEFr1qyZrF692sZ29t/SWhbyxTqfDaLmNLCQjJtUSFHYUqFHt6ETwNscfyCnUbXQI+ASwN9//y3Dhg0zapNaQ0Mzbfny5S6ucuMRhANihYECfFBjs9bg7FJpdYN+OC9u7Pzxco/C5oUS7aSFgNbW8AfKNPPggw8Ktt5WQWvUqJFg40eazCBAYcuMfGAsbAjoHCgU0kwxo0ePFhyOooJ22WWXCbbmpsksAhS2zMoPxuY/AlowrXOi0gnnkUceERxfp4JWv359cZrCkM54Mux/CWj5cRrBDZMTF8GHSTfL/dbaWrrFY/z48cYBwypoOAVq7ty5WU4396NPYcv9PM7KFGLOWjrnraFj++yzzzZraDinc/bs2VnJMh8j7UfY0JeLmp3TiC78wnOUCS+GNTYvlGgnUgI4WPjcc881Ba169eoyY8aMSOPAwFIn4EfYdAK40yRhvyPzFLbU848+BERgypQpAhHTJifE7cUXXwzId3oTNQE/wqZ27VoIOjLvZx4lhS3q3GZ4hQhAvGrVqmUKWpUqVQQiR5PdBFSsvAwe6EJ86xpXTX0yq14obEqP18gJYCvrCy+80BQ0FGA0Q2lyg4AfYUOKUVOPH4HXJqpdTc6NEoXNjQ6fhULglVdeEUzV0CYnpnBMnDgxlLDoafoI+BU27UfTGGMVBXaUsVv7qnacrhQ2JzK8HziBOXPmCCbTqqBVqFBBxo0bF3g49DAzCPgVNp1epLHX2prTgILas7tS2Oyo8F6gBObNmycNGzY0Ba1cuXIyduzYQMOgZ5lHwK+wqZDBndbWUItLxlDYkqFGN54IvPHGG8bcI62hoVmBY+Jo8oOAX2HDHDWUFbhTkUt2cjiFLT/KWKSpXLRokWDLIBW0kiVLyvDhw+XIkSORxoOBpZeAX2FT+xAzvATjBxL8pIbC5ocW7boSWLp0qWBTRxW04sWLy9ChQ+XQoUOu7vgwNwmoUHmZ7gECutOv7hsH98kaCluy5OjOJLBixQrBttsqaMccc4wMGjRI9u/fb9rhl/wj4FfYQEjLkN18Nj8EKWx+aNFuDAHsTosCqIWxaNGics8998hvv/0WY48/8pNAMsKGox1RnlLd1JTClp9lLqVUr1mzRnB0nQoarjg4Zc+ePSn5S8e5RcCvsKFvDWUpiE1NKWy5VZZCTQ1OeMLhwlZB69Wrl+DMThoSiCfgR9gwvaNy5cpJTcaNDxe/KWx2VHgvhgDW8XXo0CFG0Hr06CE4VZ2GBJwIeBU2iBpO3MIL0+u2RE5h6n0Km5LgtRCBTZs2yR133BEjaHfeeafs2LGjkF3eIIF4AomEDf1pGDFFTS2oJqjGgcKmJHg1CXz22WcCAbM2OdHvsW3bNtMOv5BAIgKJhA0DT5irhk8yy6bcwqewudHJs2fbt28XNDGtgoYm6ObNm/OMBJMbBIFEwhZEGE5+UNicyOTR/a+++kowCHD00UebooZBgo0bN+YRBSY1aAIUtqCJ0j9PBL755htjmsZxxx1nClq7du0Eo580JJAqAQpbqgTp3heBH374wZhIW6JECVPQWrduLZifRkMCQRGgsAVFkv64EsAEWix1KlWqlCloWAq1atUqV3d8SALJEKCwJUONbjwT2Ldvn7EYvWzZsqagYbH68uXLPftBiyTglwCFzS8x2vdEAIvQH3jgATnllFNMQWvevLksXrzYk3taIoFUCFDYUqFHt4UI/PXXX8aGjqeffropaE2bNpW33nqrkF3eIIGwCFDYwiKbZ/7+888/MmbMGKlUqZIpaI0aNZJkdyHNM3xMbsAEKGwBA81H7x599FE566yzTEFr0KCBzJ07Nx9RMM0ZQoDCliEZkY3RmDBhgpxzzjmmoF188cUye/bsbEwK45xjBChsOZahUSQHuyCcf/75pqDVrVtXZs6cGUXQDIMEPBGgsHnCREsggJPSa9asaQoadkiYOnUq4ZBAxhGgsGVclmRehCZPnix16tQxBa1GjRrywgsvZF5EGSMS+I8AhY1FwZEAxKtevXqmoFWrVk0gcjQkkOkEKGyZnkNpiB+al5deeqkpaFWqVDGaoWmICoMkgaQIUNiSwpabjjAAcPnll5uCht1Fg9ouOTeJMVWZSoDClqk5E2G8MEUDO4nqJo8VK1YUTOWgIYFsJUBhy9acCyDemER71VVXmYJWoUIFwWRbGhLIdgIUtmzPwSTiP3/+fLnmmmtMQStfvryxHOrIkSNJ+EYnJJB5BChsmZcnocXojTfekOuvv94UtJNOOklGjRolWLhOQwK5RIDClku56ZCWRYsWyY033mgKWsmSJY0thbC1EA0J5CIBClsu5up/aVqyZIm0bdvWFDRsxz106FD57bffcjjVTBoJiFDYcrAUYHfaW265xRS0Y489VgYPHiw///xzDqaWSSKBwgQobIWZZO2dlStXyu23324K2lFHHSUDBgyQ77//PmvTxIiTQDIEKGzJUMswNx988IF06tTJFDTMR+vbt6/s2rUrw2LK6JBANAQobNFwDiWUdevWSdeuXWMEDYcPf/nll6GER09JIFsIUNiyJacs8fz444+le/fuMYJ29913y7Zt2yy2+JUE8pcAhS2L8v7TTz+Vnj17CvrOdPlTt27dZPPmzVmUCkaVBMInQGELn3HKIWzZskV69+4tGN1UQevcubNs2LAhZb/pAQnkIgEKWwbnKpqW/fv3l+LFi5uC1rFjR1m/fn0Gx5pRI4H0E6CwpT8PCsUAnf8DBw4UrBDQGlr79u0FgwVOBrW3J5980jjTc/r06UnV5uAHpozs3LnTKRjeJ4GsIEBhy6BswvSMIUOGCNZwqqC1a9dOMJ3DySADmzRpYtpXd7ji/t69e52cxtyHqJUpU8bwZ8SIETHP8APng2JrI/1MmzatkB3eIIFMIUBhy4Cc+O6772T48OGCXTZUmNq0aWPUntyiB9GC/dKlSwvESPvckKmtWrUynuGsAi8GB7PAH/gXL2zwF/5ZRRJ9fAiHhgSCILBq1SoJ8vPUU08ZZRkv96hNkagDzLTwfvrpJ0NETjvtNCMTICo33HCDLFu2zHNUUZOyCo7VYUFBgeFvIgGCkKmg6dXqT79+/Qo1TxEmxI6GBFIlgG20sHPzPffcE9jn5ptvprClmjF+3f/6668yevRowU61EBJ8rrvuOsGi9SCNCpbb9t5aZYd46ff4GpuTgKFZSkMCqRKAsI0ZMyZVb2Lca1lmjS0GSzg/fv/9d3nkkUcEZwmooDVv3lywrVAYRoXNqcaGWhfigmYovmthiBc2CGO8OMJuvL0w0kA/c58AhS1L8/jgwYMyfvx4qVq1qiloF1xwgbRs2TLUFEGwIKBOo5zoJ8Nza98cftsJFmptI0eONPr9cEVtzakJHGqi6HnOEaCwZVmWHj58WCZOnCjnnXeeKWhXXHGFICNhsPnjpk2bQkmV1r6cmpHom4sXMXVjJ2yIJNzgGa40JBAUAQpbUCQj8Ofpp58WnJgO8cCnQYMGgsNTrAZTJoLuW4D/2sTEKKddbQ3PMbUjvo8skbBZ487vJBAUAQpbUCRD9GfSpElGn5UK2iWXXCI43s7O7NmzxziYGE3VoAxEC1M8EL7TXDMImp3oUdiCygX644cAhc0PrYjtPv/883LRRReZNTR8f/nllxPGYtCgQYJDVoIy2q/mJGoYBIDo2TUnKWxB5QL98UOAwuaHVkR2X3rpJUGtTGtoEBYnUbGL0uLFiwVTLYIwOhjgFD6apWiC4oMBgPhPly5djHRgiBzPnPwJIq70gwSUAIVNSWTAdcaMGUa/mQoa+tNeeOEF3zFDM7RevXpy4MAB326tDhKJGuxqjUzjnOga3wdnDY/fSSAoAhS2oEim4M+sWbMEI5sqChjxnDx5cgo+ivTp00dWrFiRtB9eRA2eo/8N4ub00WYq/IMdnQaSdMTokAQ8EKCweYAUlpU5c+bIlVdeaQoa5qQ9++yzgQSH2h/muSVjvIqaF7+1Ruc03cOLH7RDAn4JUNj8EgvA/rx58+Tqq682BQ0z9bE9UJAGO+NinzW/RmtY6DNDv5jbx4vfFDYvlGgnaAIUtqCJuvi3YMECadGihSlolSpVkgkTJsiRI0dcXCX36O+//zb62Q4dOuTLA9SstEmc6OrFYwqbF0q0EzQBClvQRG38W7hwobHDhgoFdt4YN26c/PXXXza2g7t12223ydatW4PzkD6RQJYQoLCFmFGYdoE90FTQsDfa2LFjZf/+/SGG+n+vhw0bJm+//fb/b/AbCeQJAQpbCBmNvc907yaIWtmyZWXUqFGyb9++EEJz9hIrFpKZLuLsI5+QQHYQoLAlkU9o3mGH2niD/iQ0/7SGVqpUKXnwwQfll19+ibcayW8MUoSxbjSSyDMQEkiBQJjChg0sozah7qCLjv4KFSqYwoURw7Vr18r7779vjECqoJUoUULQDMRutuk0ENoBAwakMwoMmwTSQiBoYcOqmRNPPNH872MTVxxhGZUJTdgwJ0yFy3q1nsuJ74MHD7atzUUFwBrOJ598Ypzubr3H7ySQDwSCFLahQ4fa/vfPOuss+fPPPyPBGZqwWWtqVmHD96JFixo1I9SQMumDSbrYTTeT4sS4ZFYZydX8eOihh6Rbt24pl/133nlHjjrqKFthw3//8ccfz15hQ59avJjx9797wpEDOeRzGcAgYRQmlBobBgrcMq9cuXKuM/TdZu/zmfvqBvIhn3SWAWwm4fbf79GjRxS6JqEIG2IOuE4JxDZDNCRAArlJoGbNmo7//SD3PXSjF5qwrVu3LuY0dRW5qKqibonmMxIggfAIoJ/t6KOPLiRu3bt3Dy/QOJ9DEzaEs3v3bmMaR9OmTaVt27YyderUuOD5kwRIIBcJfP755zJw4EBp1KiR3HrrrY5b84eV9lCFLaxI018SIAEScCNAYXOjw2ckQAJZSYDClpXZxkiTAAm4EaCwudHhMxIggawk4FvYdBtsp9PNs5ICIx0oAczOx1pBu/MacA/P7I4eDDQS9CzrCeB8EJQVTB3DDtWYWYHds1u3bi3Tp093TZ8vYUOh1GkbPD3JlWteP4SwoZzgJWg1evQgDoq2Ez2rXX7PbwLWnalRXqA3+OiZvYn0x5ewwTMEAs+hoDQk4EQAZQXihrcuDK516tQx7lHUnKjxPghoq7CgoMD2XF28IPFxM56FTd/COFhYC62bx3yW3wTQ1ISw6WlbWlh5AHR+l4tEqdfDkVB50pdiIjd2zz0LGwJCbQ1KqYWUb147pLynBPDGRZ+IFla8FGlIwIkAhEz70hLVyJz80PuehA1vWevbV9u/qMXRkIATAS03dv1tTm54P38J4MWHshLEC9CTsOHNi9qaVg31DYwrDQk4EdDuCxRWLTtOdnmfBKAzKCup1tZAMqGwae1M+0rgSAus9R6zhQSsBKzNChRW9q1Z6fB7PAGdcQFxC8K4CpsWTmttDYGqsHEuWxBZkHt+oNxgBBTlBmUFV/S10ZCAEwEdbIqfIuRkP9F9V2HT2ho69OI3r8NbONFckkSB83luEtDBJa2lad8JRI6GBOwIqNYE1Qp0FDa0cyFebh/OZbPLovy+pwXU2gGsZQkvRxoSsCOg5SZ0YYt/68ZHhnPZ4onwt46C2tXktTxxihDLiR0BFbZQm6JeOvJU2FhQ7bIpP++hcOJjNwKKcoJnbI7mZ9lIlGrtYwuqL9a2Kaqi5VYIVWHd7CRKDJ+TAAmQgBLAIBO6voKYRlZI2CBUXgYGVNiCiIQmjFcSIIH8JaBdGdCf/v37y8qVKw0Y0KQFCxYY97zSKSRsuno+UU1Mq44QOBoSIAESCIIAxE1rbnYDl17DKCRsXh3SHgmQAAmEQQB9tBA4VJr0g99+ViRQ2MLIGfpJAiSQVgIUtrTiZ+AkQAJhEKCwhUGVfpIACaSVAIUtrfgZOAmQQBgEKGxhUKWfJEACaSVAYUsrfgZOAiQQBgEKWxhU6ScJkEBaCVDY0oqfgZMACYRB4H+mtUC60BAQBwAAAABJRU5ErkJggg==[/img]
An equilateral triangle has area of [math]36\sqrt{3}[/math] square units. What is the side length?