[size=100][justify][b][size=200][/size][size=200]Triângulo de Sierpinski[br][br][/size][/b]O Triângulo de Sierpinski é um exemplo de fractal autossimilar. Ele recebe esse nome em homenagem ao matemático polonês Wacław Sierpiński, que foi o primeiro a descrever essa estrutura.[/justify][/size]

[size=85][center]Figura 1: Wacław Sierpiński[/center][/size]
[size=150][b]Como o Triângulo de Sierpinski é formado? [/b][/size]
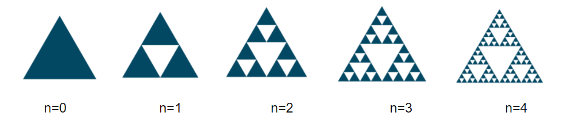
[center][size=85][/size]Figura 2: Construção do Triângulo de Sierpinski [size=85][/size][/center]
[justify]É possível construir o Triângulo de Sierpinski através de um processo iterativo que tem como ponto de partida um triângulo equilátero.Na primeira iteração determina-se os pontos médios de cada lado dessa figura e une-se esses pontos. Depois, remove-se o triângulo do meio.Na segunda iteração esses passos são repetidos para cada um dos triângulos restantes.Esse processo pode ser repetido indefinidamente, dando origem ao famoso fractal conhecido como Triângulo de Sierpinski.[/justify][justify][/justify]

[center][size=85][/size]Figura 3: Triângulo de Sierpinski [size=85][/size][/center]
[b][size=150]Propriedades do Triângulo de Sierpinski [/size][/b]
[justify]Note que o ponto médio de cada lado do triângulo inicial se torna um vértice de um novo triângulo. Assim, os triângulos gerados na próxima iteração possuem metade do comprimento e metade da altura do triângulo inicial. Além disso, cada novo triângulo possui ¼ da área do triângulo a partir do qual foi gerado.Apenas observando a figura 2 também é possível notar que na primeira iteração surgem 3 novos triângulos. Na segunda iteração, é possível identificar 9 triângulos. Na terceira iteração existem 27. Seguindo esse padrão, na iteração de ordem N existirão 3[sup]N[/sup] triângulos.[/justify]