Special Lines and Centres of triangles

Arthur Lee, GeoGebra Institute of Hong Kong, May 1, 2024

Special Lines and Centres of Triangles

Table of Contents

  1. Empirical Explorations
    1. Lines in a Triangle
    2. Centres in a Triangle
  2. Soft Construction Exploration
    1. Circumcircle of a triangle (Soft Construction)
    2. Incircle of a triangle
    3. Trisecting a Triangle
  3. Special Lines
    1. triangle fold
    2. bisector of a triangle
    3. River excursion
  4. Miscellaneous
    1. Special Lines & Centres of Triangles 三角形的特殊線和中心
    2. Quiz on Special Lines in Triangles 三角形內的特殊線：測驗
    3. Quiz on Centres of Triangles 三角形的中心：測驗
    4. perpendicular bisectors
    5. where perpendicular bisectors intersect
    6. perpendicular bisectors and angles
    7. 6 mid-points
  5. 3D
    1. dumpling model
    2. Tetrahedron Net (general)
    3. Centroid of tetrahedron (I)
    4. Centroid of tetrahedron (II)
    5. Circumcenter of tetrahedron
    6. Incenter of tetrahedron
    7. Making of tetrahedron with given insphere
  6. More Online Resources
    1. orthocentre coordinates
    2. Centres of data / triangles
    3. introduce Voronoi diagram in Desmos

1.

Empirical Explorations

  • 1. Lines in a Triangle
  • 2. Centres in a Triangle

1.1.

Lines in a Triangle

1 Lines in a Triangle
– Anthony OR 柯志明

1.2.

–

2.

Soft Construction Exploration

This section suggests some exploratory tasks based on the concept of 'soft construction'. You may find out more from another collection by Anthony Or: https://www.geogebra.org/m/VytTQugN including his article: Or, A. C. M. (2013). Designing tasks to foster operative apprehension for visualization and reasoning in dynamic geometry environment. In C. Margolinas (Ed.), Task design in mathematics education: Proceedings of ICMI Study 22 (pp. 89–98), Oxford, UK. Available from https://hal.science/hal-00834054v3

  • 1. Circumcircle of a triangle (Soft Construction)
  • 2. Incircle of a triangle
  • 3. Trisecting a Triangle

2.1.

Circumcircle of a triangle (Soft Construction)

([i]Drag the three vertices of the triangle to change its shape.[/i])[br][br]Drag the blue point to A.[br]Drag the centre (the red point) to different positions at which the circle also passes through B.[br]Observe the marks of these positions. What are their characteristic?[br][br]What is the charateristic of the positions of the centre at which the circle passes through A and C?[br][br]How to draw the circle which passes thorough A, B and C?
Anthony Or. GeoGebra Institute of Hong Kong.
– Anthony OR 柯志明

2.2.

–

2.3.

–

3.

Special Lines

This section focuses on the meaning and properties of special lines (particularly those bisectors) related to a triangle (or part of a triangle). The 'river excursion' task is part of a collection about Voronoi Partitioning: https://www.geogebra.org/m/Ff6ZJdux

  • 1. triangle fold
  • 2. bisector of a triangle
  • 3. River excursion

3.1.

triangle fold

This is a triangle folding activity.[br][br]A and B are movable points. You can make a fold by dragging point C. Turn off the grid if needed. [br][br]What tasks or questions will you try for exploring properties of a triangle?
How about trying these:[br][list][*]make a fold to:[br][/*][/list] bisect angle A; angle B[br] bisect side BC; AC[br] add the altitude from A; from B[br][list][*]does the angle bisector of A bisect BC? when?[/*][*]show that longer side is opposite to greater angle[/*][*][size=100]cover point A, drag B to make angles B and C almost equal, fold C to B and compare the angles in order to tell which opposite side is longer[/size][br][/*][/list]
– Arthur Lee

3.2.

–

3.3.

–

4.

Miscellaneous

  • 1. Special Lines & Centres of Triangles 三角形的特殊線和中心
  • 2. Quiz on Special Lines in Triangles 三角形內的特殊線：測驗
  • 3. Quiz on Centres of Triangles 三角形的中心：測驗
  • 4. perpendicular bisectors
  • 5. where perpendicular bisectors intersect
  • 6. perpendicular bisectors and angles
  • 7. 6 mid-points

4.1.

Special Lines & Centres of Triangles 三角形的特殊線和中心

問題
[list=1][*]顯示三角形ABC的中線和形心G。量度AG和GA’。它們有甚麼關係？[br]類似地，BG和GB’、CG和GC’有甚麼關係？[/*][*]量度三角形AGB’和其餘五個三角形的面積(要先用多方形工具構作該六個三角形)。[br]它們有甚麼關係？[br][/*][*]顯示三角形ABC的垂直平分線和外心O。量度OA、OB及OC的長度。它們有甚麼關係？[br]嘗試以O為圓心繪畫一個圓形通過A、B及C(該圓稱為三角形ABC的[b]外接圓[/b])。[br][/*][*]顯示三角形ABC的角平分線及內心I。由I作垂直線到三角形ABC的三邊。量度I與三點垂足的距離。它們有甚麼關係？[br]嘗試以I為圓心繪畫一個圓形使它相切於三角形ABC的三邊(該圓稱為三角形ABC的[b]內接圓[/b])。[br][/*][*]顯示三角形ABC的四個中心(但隱藏各特殊線)和格線。[br]當ABC為[i]等腰[/i]三角形時，G、H、O和I有何特徵？[br][/*][*]當ABC為[i]直角[/i]三角形時，H和O有何特徵？[br][/*][*]當ABC為[i]鈍角[/i]三角形時，H和O有何特徵？[br][/*][*]甚麼情況下G、H、O和I會重合？[br][/*][*]G、H、O和I四者中，哪三者永遠共線(在同一直線之上)？它們之間的距離又有甚麼關係？[/*][/list]
gMath 互動數學教室[br][url=http://www.gmath.hk]http://www.gmath.hk[/url]
– Alex CHIK

4.2.

–

4.3.

–

4.4.

–

4.5.

–

4.6.

–

4.7.

–

5.

3D

This section shows some examples about special lines and triangle centres in 3-dimensional space.

  • 1. dumpling model
  • 2. Tetrahedron Net (general)
  • 3. Centroid of tetrahedron (I)
  • 4. Centroid of tetrahedron (II)
  • 5. Circumcenter of tetrahedron
  • 6. Incenter of tetrahedron
  • 7. Making of tetrahedron with given insphere

5.1.

dumpling model

This is a rice dumpling model in the shape of a tetrahedron with 4 faces of isosceles triangles. In the 3D model on the right, you may drag D, E and F to fold faces. [br][br]Imagine where the faces will meet. Make a guess and use the checkboxes to find out more about the shape.
If you drag C on the left, the 4 triangles will be changed but remains congruent. How would you describe, in general, which point on the plane will be the projection of the apex? [br][br]Check another version where the faces can be changed individually:[br]https://www.geogebra.org/m/hdgmkgsa [br][br]or this version, focusing on its apex and altitude:[br]https://www.geogebra.org/m/wdkbbq49
– Arthur Lee

5.2.

–

5.3.

–

5.4.

–

5.5.

–

5.6.

–

5.7.

–

6.

More Online Resources

  • 1. orthocentre coordinates
  • 2. Centres of data / triangles
  • 3. introduce Voronoi diagram in Desmos

6.1.

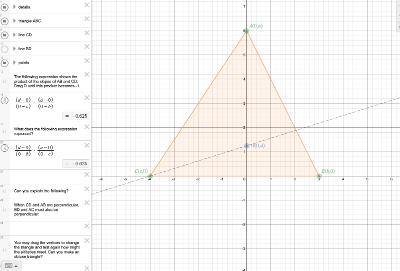
orthocentre coordinates

The property of altitudes and orthocenter can be studied easily in the coordinate plane. [br][br]Here is an example using Desmos calculator:[br][url=https://www.desmos.com/calculator/qrkzyjvdli]https://www.desmos.com/calculator/qrkzyjvdli[/url]
– Arthur Lee

6.2.

–

6.3.

–

Information