Sinus & Co
Diese Unterrichtseinheit entstand im Rahmen der Initiative "Mathe.Forscher meets GeoGebra". Weitere Informationen zum Mathe.Forscher-Programm findet man auf [url]www.Matheforscher.de[/url].
Table of Contents
- Schattenlängen untersuchen
- Experiment zur Einstimmung
- 1) Schattenwurf erkunden
- 2) Schattenlängen erforschen
- Sinus- und Kosinuswerte erforschen
- 3) Werte schätzen
- 4) Exakte Werte begründen
- 5) Exakte Werte kennen
- Bogenmaß erkunden
- 6) Bogenmaß erkunden
- Hin und her - Pendelgraphen entdecken
- 7) Der Sinusgraph
- 8) Der Kosinusgraph
- 9) Pendelgraphen in der Röhre - 3D
- Symmetrien nutzen - Gleichungen lösen
- 10) Symmetrien entdecken - Trigonometrische Uhr
- 11) Symmetrie am Graphen - "Beistift-Trigonometrie"
- Bonustrack - Crazy Circle Illusion
- 12) Crazy Circle Illusion
Experiment zur Einstimmung
Die beiden Farb-LED-Lampen im Bild oben wurden so eingestellt, dass der Bleitstift von oben mit rotem und von rechts mit blauem Licht bestrahlt wird. Der untere Schatten des Stifts enthält dann keine Rot-Anteile und erscheint daher blau. Der Schatten links an der Wand erscheint dagegen rot, da hier die Blau-Anteile fehlen:
Der Bleistift ist dabei drehbar gelagert und über ein abgewinkeltes Metallstäbchen mit einem kleinen Rotationsmotor hinter der Holzplatte verbunden. Im folgenden kurzen Videoausschnitt kannst du beobachten, wie sich die Längen der beiden farbigen Schatten bei der Rotation des Bleistifts verändern:
3) Werte schätzen
Wie wir gesehen haben, entspricht die positiv oder negativ [i]orientierte[/i] Länge x des blauen Schattens (in dm) dem Kosinus- und die des roten Schattens y dem Sinuswert des Drehwinkels. Für 0°[math]\le[/math]α[math]\le[/math]90° befindet sich P wie im Bild zu sehen in Quadrant I und beide Werte sind positiv.
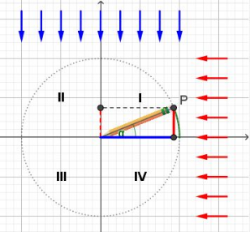
[u]Auftrag 1[/u]:[br]Erzeuge im folgenden Applet durch Klick auf die grüne Schaltfläche (0°[math]\le[/math]α[math]\le[/math]90°) einen zufälligen Winkel (in Quadrant I). Deine Aufgabe ist es, für[color=#ff0000] y=sin(α)[/color] und [color=#0000ff]x=cos(α)[/color] Schätzwerte einzutragen, die um höchstens 0.05 (dm) vom tatsächlichen Wert abweichen. Viel Erfolg![br][br][i]Tipp: Mit einem der beiden Schatten bleibt es übersichtlicher. Mit etwas mehr Sicherheit kannst du später dann auch Sinus- und Kosinus-Werte gleichzeitig schätzen. [/i]
[u]Auftrag 2[/u]:[br]Erweitere deine Untersuchung im nächsten Applet auf Quadrant II (90°[math]\le[/math]α[math]\le[/math]180°).[br][br][i]Tipp: Sinus- und Kosinus-Werte können auch negativ sein, achte daher genau auf die Vorzeichen![/i]
[u]Auftrag 3[/u]:[br]Nun kannst du den Vollkreis untersuchen. Erzeuge durch Klick auf die Schaltfläche 0°[math]\le[/math]α[math]\le[/math]360° zufällige Winkel und trage wieder deine Schätzwerte ein.[br][br][i]Tipps: Die Gitternetzlinien helfen dir beim Schätzen. Achte wieder auf die wechselnden Vorzeichen![/i]
[u]Auftrag 4[/u]:[br]Nun bist du fit für [i]Besondere Werte mit 0°[/i][i][math]\le[/math]α[math]\le[/math]360°[/i] ![br]Welche besonderen Drehwinkel werden hier zufällig ausgewählt?[br]Schätze wieder die zugehörigen Sinus- und Kosinus-Werte, die wir noch häufiger verwenden werden.[br][br][i]Tipp: Diese Werte kannst du dir auch in der Tabelle auf Entdeckerblatt 2 nochmals ansehen.[/i]
6) Bogenmaß erkunden
Statt die Weite eines Winkels wie bisher im [i]Gradmaß[/i] anzugeben (z.B. [math]\alpha[/math]=45°) , kann man auch die Länge des zum Winkel gehörenden Einheitskreisbogens b messen, das sogenannte [i][color=#6aa84f]Bogenmaß b.[/color][color=#6aa84f][br][/color][/i]
Auftrag 1
Erkunde mit dem folgenden Applet den Zusammenhang zwischen Einheitskreis und [i][color=#6aa84f]Bogenmaß[/color][/i] [i][color=#6aa84f]b[/color][/i] für verschiedene Winkel. Beschreibe dann auf dem begleitenden Arbeitsblatt (oder im Heft) den Unterschied zwischen [i]Grad[/i]- und [i]Bogenmaß [/i]mit deinen Worten.
Auftrag 2
[i][size=100]Bearbeite die folgenden Aufgabenteile auf dem begleitenden Mathe.Forscher-Arbeitsblatt oder wahlweise im Heft: [/size][/i]
c) Berechne die Werte und fülle die Tabelle aus. Gib das Bogenmaß dabei auf zwei Dezimalen gerundet an.[br]Bei korrekten Werten erscheint ein grüner Haken. Übertrage diese Werte zur Ergebnissicherung dann auch in die Tabelle auf dem Arbeitsblatt.
Auftrag 3
Erkunde die Zusammenhänge nun mit dem folgenden Applet genauer. Dabei kannst du u.a. beobachten, wie das Bogenmaß b bei wachsendem Drehwinkel [math]\alpha[/math] auf der x-Achse abgetragen wird.[br] [br][u]Übungen zur Umrechnung vom [i]Grad[/i]- ins [i]Bogenmaß[/i][/u]:[br]Nach Klick auf die Schaltfläche "[i]Neue Aufgabe[/i]" kannst du das zugehörige Bogenmaß jeweils als Vielfaches von π eingeben, z.B. in der Schreibweise 4/3 π oder auch mit Dezimalpunkt in der Form 1.33 π.[br][br][u]Anmerkungen zum [i]High-Score[/i][/u]: [br]Korrekte Antworten werden gezählt und der Rekord angezeigt. Allerdings wird der Zähler bei einer falschen oder ausbleibenden Antwort jeweils auf null zurückgesetzt. [br]Auf geht´s, viel Erfolg!
[b]Hinweis zur geometrischen Deutung und Umrechnung[/b][br]Jeder Winkel lässt sich als geeignetes Vielfaches einer "180°-Drehung" deuten. Bei einer solchen Halbdrehung legt ein Punkt auf dem Einheitskreis die Bogenlänge π LE zurück. Daher kann man Winkel auch als Vielfache von π angeben. Dies ist u. a. bei der Umrechnung vom Grad- ins Bogenmaß oder umgekehrt hilfreich, z.B. [math]20°=\frac{1}{9}\cdot180°=\frac{1}{9}\cdot\pi=\frac{\pi}{9}\approx0.35\left(LE\right)[/math].
7) Der Sinusgraph
Hier kannst du nun den Graphen der Sinus-Funktion entdecken.[br]Der Punkt P (das "Bleistift-Ende") startet wie gewohnt rechts in der Mittellage und wandert entgegen dem Uhrzeigersinn auf dem Einheitskreis. Schaue dir in der folgenden Animation zunächst die vertikale Pendelbewegung an, die der [color=#ff0000]rote Bleistiftschatten[/color] erzeugt, wenn der Bleistift seitlich von rechts oder links angestrahlt wird.[br]
Auftrag 1
Die beim Hin- und Her-Pendeln auftretenden Sinus-Werte werden nun für eine Kreisumrundung in 30°-Schritten (im Gradmaß) bzw. in [math]\frac{\pi}{6}[/math]-Schritten (im Bogenmaß) als Funktionswerte in ein Koordinatensystem übertragen. Falls du die Werte nicht auswendig kennst, kannst du einen TR verwenden. [br]Gib dann im folgenden Applet jeweils den zugehörigen Sinus-Wert auf zwei Dezimalen gerundet ein. Bei korrekter Eingabe erscheint ein grüner Haken und die Schaltfläche "[i]weiter...[/i]" für den nächsten Schritt.[br]Trage die Werte auch fortlaufend in die Tabelle auf dem begleitenden Arbeitsblatt ein.[br]Die Tabelle benötigst du später bei Aufgabe 2 zum Zeichnen des Graphen der Sinus-Funktion.
Auftrag 2
Zeichne mithilfe der Wertetabelle nun selbst den Graphen der Sinus-Funktion f mit f(x)=sin(x) in das vorbereitete Koordinatensystem auf dem Arbeitsblatt.[br]Skizziere dabei seinen Verlauf auch für die zweite Kreisumrundung im Bereich 2π≤x≤4π:
Auftrag 3
Fülle für α= 45°, 135°, 225° und 315° die grau unterlegten Tabellenspalten aus und ergänze die zugehörigen Punkte im Schaubild der Sinusfunktion (s. Auftrag 2).
10) Symmetrien entdecken - Trigonometrische Uhr
Mit einer trigonometrischen Uhr kannst du die Zusammenhänge am Einheitskreis dynamisch erkunden und so noch besser verstehen. Die folgenden digitalen Simulationen helfen dir dabei.[br]Noch wirkungsvoller und überzeugender ist eine echte trigonometrische Uhr, die du dir mit der Anleitung ganz am Ende dieser Aktivität selbst bauen kannst. Aber zuerst mal der Reihe nach ...
Auftrag 1: Trigonometrische Uhr erkunden
Erforsche mit dem Applet oben das Funktionsprinzip und beschreibe mit Stichworten, was man an dieser Uhr einstellen und ablesen kann. Gehe dabei auch auf die Bedeutung der [color=#6aa84f]grünen Bögen[/color] und der [color=#ff0000]roten[/color] bzw. [color=#0000ff]blauen[/color] Strecken ein:
Auftrag 2: Bist du fit? Pendelschatten ablesen
Klicke im folgenden Applet auf "Neue Aufgabe" und stelle die Uhr auf den vorgegebenen Drehwinkel ein. Lies dann den Sinus- und Kosinus-Wert möglichst genau ab und trage beide in die Antwortfelder ein:
Auftrag 3: Fünfzehn Grad - Pi Zwölftel?!
Mit dem nächsten Applet kannst du Sinus- und Kosinus-Werte für besondere Winkel ermitteln und überprüfen. Falls du das Bogenmaß kennst, kannst du hier auch den Wechsel zwischen Grad- und Bogenmaß in einem für dich passenden Tempo wiederholen. Als Drehwinkel wird jeweils ein Vielfaches von 15° (bzw. [math]\frac{\pi}{12}[/math] im Bogenmaß) vorgegeben. Gehe vor wie bei Aufgabe 2.
Auftrag 4: Symmetrien entdecken – Gleichungen lösen
Nun wird eine zufällige Sinus- oder Kosinus-Gleichung generiert. Suche mit der Uhr möglichst viele Lösungen und gib zwei davon ein. Anfangs kann es sinnvoll sein, sich einen Tipp geben zu lassen … Erforsche die auftretenden Zeiger-Symmetrien, beschreibe sie mit deinen Worten und visualisiere sie in den beiden Einheitskreis-Diagrammen auf dem Arbeitsblatt. Kannst du auch die Gleichungen in den Kästen ergänzen?
Anlage: Vorlage zur Herstellung einer trigonometrischen Uhr
12) Crazy Circle Illusion
Auftrag 1
Starte die Animation, beobachte die Punkte und beschreibe unten deine Beobachtungen ...[br]
Beschreibe die Bewegung der weißen Punkte mit deinen Worten:
Auftrag 2: Analyse der Illusion
Starte im folgenden Applet erneut die Bewegung der Punkte. Sobald du die Hilfsstrecken einblendest, verschwinden die Punkte und du kannst sie danach einzeln zeitversetzt einblenden, um den Weg jedes Punktes genauer verfolgen zu können und die Illusion zu analysieren. Diesen Vorgang kannst du bei Bedarf mehrmals wiederholen und die Punkte dabei auch ein- und ausblenden ...
Auftrag 3: Vermutung formulieren und überprüfen
Ergänze nun deine erste Beschreibung der Bewegung um weitere Beobachtungen.[br]Wie entsteht die Illusion eines rollenden Kreises? Beschreibe deine Vermutung.
Crazy Circle Illusion
Um deine ersten Vermutungen zu überprüfen, kannst du dir nun das folgende Video ansehen, das diese optische Täuschung sehr gut darstellt und im zweiten Teil zeigt, wie jeder Punkt zeitversetzt auf einer geraden Strecke um den Mittelpunkt des großen Kreises pendelt.
Vertiefter Einblick - Bonustracks ...
Falls du Interesse, Zeit und Lust hast, kannst du nun dieses Hin- und Herpendeln eines einzelnen Punktes mit einer Sinusschwingung modelllieren oder auch gleich die komplette Illusion mit der Schritt-für-Schritt-Anleitung erzeugen, die du ganz unten aufrufen kannst.[br]Oder vielleicht hast du auch nur jeden zweiten Punkt eingeblendet und ein sich drehendes Quadrat entdeckt, das du nun mit einer eigenen Animation zum Leben erwecken möchtest ...
Auftrag 4: Sinusschwingung eines einzelnen Punktes erzeugen
Im folgenden leeren GeoGebra-Applet ist der Mittelpunkt M des großen Kreises bereits vorgegeben. [br]Ergänze die Konstruktion durhc folgende Eingaben:[br]1) A=(2,0) | Randpunkt rechts außen in Mittellage[br]2) t=Schieberegler(0,2*Pi) | Variable t, die eine Sinusperiode von 0 bis 2[math]\pi[/math] durchläuft[br]3) A'=M+sin(t)*vektor(M,A) | Punkt A' erzeugen, der um M pendelt
[i]Hinweis: Nach Rechtsklick auf den Schieberegler t kannst du unter "Einstellungen" [math]\longrightarrow[/math] "Schieberegler" die Geschwindigkeit erhöhen und die Wiederholung auf "zunehmend" setzen, um eine kontinuierliche Pendelbewegung zu erhalten.[br][br][/i]Kannst du beim 4. Schritt erklären, warum sich eine Pendelbewegung ergibt? Diskutiert die Frage zunächst zu zweit oder dritt, bevor die Vermutungen dann in der Klasse vorgestellt und verglichen werden.
Vertiefung? Crazy Circle Illusion!
Wenn du nocht nicht genug hast, kannst du die Zusammenhänge noch weiter erkunden. Mit der[br]nachfolgenden Anleitung ([i]CrazyCircle_Anleitung.pdf[/i]) kannst du die Illusion in einer leeren GeoGebra-Datei Schritt für Schritt erzeugen und dabei die abgestimmten Zeitverzögerungen ("Phasenverschiebungen") genauer erforschen. Viel Spaß dabei!
Crazy Circle - Anleitung
