
ALAN
Eşkenar Dörtgen' in Alanı
Yamuğu bir nokta etrafında 180 derece döndürme
Yamuğun Alanı

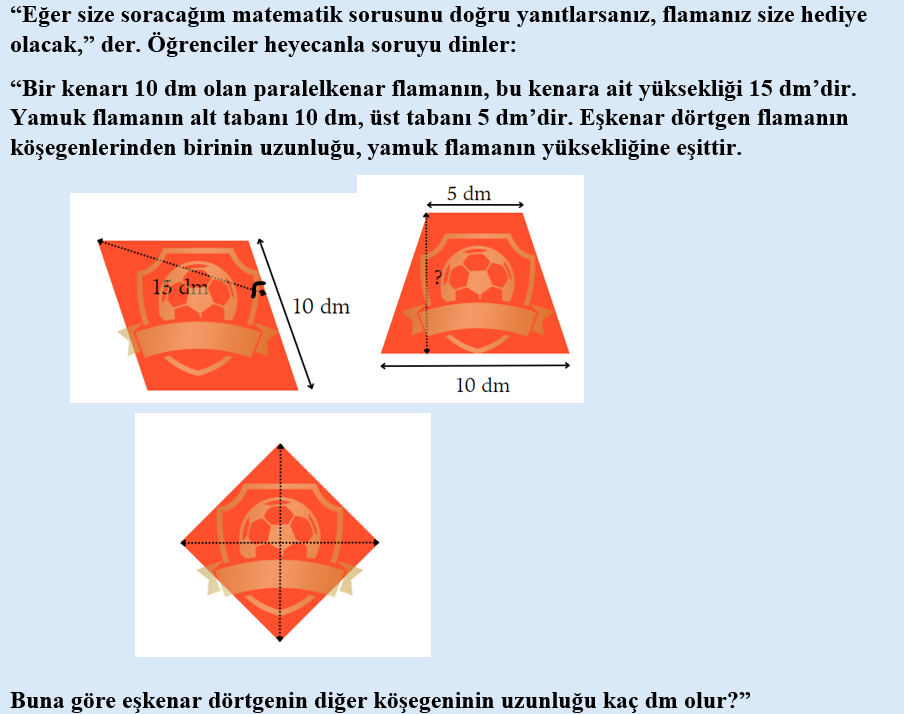

[br][br][b]“Aynı alana sahip dikdörtgenlerde kenar uzunlukları ile çevre arasında[br]nasıl bir ilişki vardır? Yani kenar uzunluklarının birbirine yakın değerler[br]olması çevre uzunluğunu nasıl etkiler?” [/b][br][br][br]
[b][u]SORU 1:[/u][/b] Çevresi 28 cm olan bir eşkenar dörtgenin bir kenarına[br]ait yüksekliği 4 cm ise bu eşkenar dörtgenin alanı kaç cm[sup]2 [/sup]dir?
[b][u]SORU 2:[/u][/b] Köşegenlerinden birinin uzunluğu 14 cm, alanı 126 cm[sup]2[/sup] olan[br]eşkenar dörtgen şeklindeki bahçenin diğer köşegeni kaç cm’dir?[br][br][br]
SORU 3:
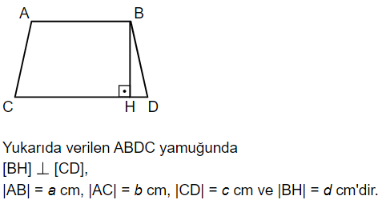
[size=150]ABCD yamuğunun alanının bulunabilmesi için, verilen uzunluklardan[br]hangisinin bilinmesine gerek yoktur?[br][br]A) |AB|[br]B) |BC|[br]C) |CD|[br]D) |BH|[/size][br][br]
[b][u]SORU 4:[/u][/b] Kenar uzunlukları birer doğal sayı olan dikdörtgenin çevre uzunluğu 16[br]cm’dir. [b]Buna göre bu dikdörtgenin alanının alabileceği [u]en büyük[/u] değeri[br]bulunuz.[/b]
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAjsAAAHiCAYAAAAODw0hAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAFxEAABcRAcom8z8AAHz4SURBVHhe7d0FWFZ5/vfxfZ5n/7MzY3cAbv53Z3d2enRsURrplBbBABVFRUzswk5QVERBkO7uLru7QMLuQj/PdQ7gKGDdgyNHPt/rel3sys0NjtyHN+f8zjl/AIfD4XA4HM4nPH+o+wccDofD4XA4n9IwdjgcDofD4XzSw9jhcDgcDofzSc87xc7zZ8/w5PEj3L51E5WVlagoL0f5KypQefUabty8jfsPHqHq2fO6T8HhcDgcDuc186zqCR7cu4vr1ypwpfQCTp84i1MnLqCkpBzXbtzCvQeP8KzuB3Heed4eO8+f48G9mzh9bC88Nq7BxIkT4ezsXGMSnCdNwaQp0zF99iKs2LANITGpOHTqIu49fFz3mTgcDofD4dSZh3dv4ezRvYgJ8cOKhW6Y4DASw61sYD18NBydpmPRCg+ExKbidHklHgk/lus+Aeet89bYef78GW5fv4LclHAMMzDA1//9CSpDtWBgbAwTYxMYG5nA2NgUJqZmMLMeAYeJM7F8/S7kFB/DnfsP8fw5/1k4HA6Hw6k7ws/Hu7euY29WKratdse0CeNga20BY2MTmJqawMTUFAZG5hhmMQITXGdjS2A4Dpy/hPtVVdzL857zTrFz61oJ0mMDoTZQHT/8rAqX+UuwYds2bPfeDu+tW7B18zqsWzEPUyaMhqGeMbR0h2Oeuxf2HjuLh0+e1n1KDofD4XCa/Tx+eBeHCzOwas4s2OgPg/0IRyxYvg47gyORkJqEpIRI7NruAbdpzrCxNIOJtT3W7QrC+es38bCKufM+886xkxEXDPWBOlDTskNQciZOXSlFRWUFKstKUVZyDudO7kVa/B4smDUFukP1MNTQFmt9glFy+y6YOxwOh8PhvDxPUVF2AptXzIGljh4sh9lj7cYdKD56GtcfPKl5zBPcrLyA3JRQLJs9EYN6/gILm7FIzD+Aylt36jwf503zXrGjNlAbWvpjkFi4Hzef1F+T8/TJDezNi8eSOS4YMEAFlo7TUXj+Iu4+q6r7UA6Hw+Fwmuk8w7Oqm9hfGAMrPQ1oaehh1SZvHD19vu4DxXlwtxx5qZEYM8wMNpZjEJaYjdKK61wm8h4jQ+yMfm3sCMumrpadRXSgN/SVNDBU3RwRaXkou3UHz/iPwuFwOBwOqqqe4HrZWQTv9MCAXoowtR6HuJwi3HwoLD9uaJ6irKwMkVGpCE/IxpnKa7j3uHbvD+ddRqbYSSjYhxuPG/5HefTgKoqzY2CvrwuVfurw2h2BMyXlqHrG44scDofD4Tx58ghnju3DuiVz8fNPQ2A3cQ7yT57Fg7oPfGkePn6Kkso7KLv1QDwjiz9R328aPXaePbuN44dSMdHGGEp9FOG+wQdHTl3Ak6c8lMXhcDgczqNHD7A/PwPzXCfgl75qmDhnBQ5eLEFDx0tqRzg48rTquXgdOx4nef9p9Nh5/vwOTh/LhOsYCyj3U8S85R7Yf/Q0Y4fD4XA4HGEvzYP7yMtIgKvTKAwYooWZ7htx8ko5+FPyw80HiZ1TxzLg6mAB5f6DMM99E/YfPcXY4XA4HA6nJnbyMxMxbeJoDFLRhdtKD5wqr+ShqQ84jR474mGsw6mYaGss7tlx37BDPIz1lNcE4HA4HA4Hjx89xMHCLCye6YIBilqYsmgNDpeU4U1Ljp9VPcPDBw9w585d3H/wEE+qqng46z2m0WPn8cNr2JtTs0C5vwa2BkThXGkF75fF4XA4HI54mZbHuHTqMLxWL0OfXuoY6TwfBafO48Eb8uVGZSUy42Lhs20nIhIzcPpKBR7wLOd3HpliRzj1/NbThhu0svQUwv29oK+qCV19W8Tl7cPVe/ff8E/I4XA4HE7zmefPnuLujcuIC90Blf7KMDEfg/CUbFy7d7/uQ8V5XvUYpw4VY/HkCbA0toT7pl3Yf/oCHvAs53cemWInPn8vrj18gKpnVaiqeoqqp4/x+OE9XKu8iJTYILhNmwR1TQNMmO2OI6XleMi9OhwOh8Ph1IxwUcE7OLI/GWOtTaE3VB8Llq5HTtEh3Hv46JWdA8+ePkT5pROICdwOc01V6OmYYPueGJy5XI4q7tl553mv2FEfqA1lDWvsikrAgdOnce78OZw7cwpnTh7GweIMhO3ZjhlTJsJAbxis7CdjV0QSrt5/wEVXHA6Hw+G8MlWoLDuNHeuWwNbIBOYmdli20gMZRQdw+fptPHz8AA/vXMX5kwcQE7wdbi6OUB2shDGTZiDjwFFcu8MjJu8z7xg7pUiPC4KGoia+76kMZ7d5WO3hAc/NnvDctBEeG1ZjxZLZmOBgD0N9UxiaOmC1ZwBOXLiCJ1yYzOFwOBxOvRGOiBwpysJKt9kw0zaGtaUdZi1aDi//YETFRCIq1A8e65ZjysQxMDc3heWo8dgaGouSO/fwmHt13mveGjt4/gy3r5UiKzEY+kPV0U2uB/7z7Xf4sWdP/NyzF37+uQ/69FPEYFVN6JkOx4RpS7BtdxxOnL2Cxw2cbi7cy+PZs2eoqhIOgREREUmf8HNN8F7zXLjrwD0czMuBh/sijLY0xpBBffHddz/g++++xXfffY9vf+oHJU1jjJs2D/6JmTh//RZvri3DvD128ByP7t/GxTNH4O/rjfnz5sJt1izMmjkTM2fOxsxZczFn/lK4r/HAjoAIZBQeFi9p3VBz3r17F0lJSZgzdw5cpk7BVFcXuBIREUnUVNcpmDbNFW5ubkhISMDjx2+6DnLD8/jBPZw7fhBxYf5Y6z4fLhMcMcpuJEaOmoAp0xdig9duJOfuRcW9h3U/lPOO8w6xI+RO9d6YJ48f49HDR3j08CEeih7h4aNHeCR6jMdPnuCpWLgNpQ5w5coVuLpOQ9u27fHXv/wT33/bC9992xPffUNERCQx3/bEt//9Gf/4+1do07otnCc5i7/Uv++IRzyqqvDkyRM8fnQfD+7dwNWK67haeRv37j3A48fVP1uFxwk/XRv+Cct507xT7DTWlJSUYMKECVCQ+xvGjXHDuhV7sHrZbqxa6ktERCQpa5YHYOWSXRg3Zjbku/8VI0fZ486dO3V/9Mkwwg4GQd0/58g6v2vsXL58WYyd/3z1AzzWhSM/vQzZyZeRlXSJiIhIUnJTryAj8QI2rgnBv//1PezsbRspdjiNPb977EycOAHffP0ztnvG40D+bRRnX0dR1lUiIiJJ2Zd7EwWZFfDaFIP//ucn2NuPYOw00fkosSN8U3htjEZx9jXkp5cjL+0KERGRpBRmViIntQSe6yPw9b9/ZOw04WHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsEBERyYCxI51h7BAREcmAsSOdYewQERHJgLEjnWHsENHvpAwFGRUoyrqK4uzr2JtzHXuzr6EoqxKFGeXITytr4GOImi7GjnSGsUNEH1x+uhAypchJuYSMhLNIjT2F5OiTSIk9jbSE88hKvoxc4bHi4+p/PFFTxNiRzjB2iOiDy08vQWbiCYT5pWPTCj8snrUGM6euwuxZW7BqRRh8d+UjMfECctPLkN/AxxM1RYwd6Qxjh4g+GGGPTn56KbKSjiPULx7L3FbC1tQO2kqaGDxQA4pKJjAynQjX2V7YsbsA6cmXUcC9OyQRjB3pDGOHiD6Yggxhnc55BO+MxMyJ02Ckaw4tLVuMHj0f06cuxxi78dDRNIC27nA4TVmLkMCD2CduF94neKof+757hF77eOFzpzfw50R1MHakM4wdIvoghNd2fsYVZMbvx/J5K6CjZgA1DStMnOaF3XtOIDv1EkJ8IuDq6AwtNUMM1XHA+o1JKMi5/pa1O8LeonIUZV3Dvtzr2J9/A0W5N1GUcwt7c26gOPsqCjKqtyvVC6KvidsagbAoen/eVezPv4a9eTfF/y8smC7IqERR9jXsy7mJA9k3cCDnBvbnvvpcRHUxdqQzjB0i+iCE0MhLK0HYrgQ4j5kONTVrjB6/HP7BB5GTWYninGvIiDuOnZtCMH3iEtjazsPqjclIy6hATgPPVys//QpyUy8jPe40EkL3IcI/B/6+eQjYvReRIUeQHHsW2Skl4tldWYkXkBp7GikxglNIijyM2KAsBO9Oxx7/vYgKO4bU+LPITr6AtLhTiNlTjIgdOYjYVYCYkMNIqXmuul8DkYCxI51h7BDRB1GYeRU5yRfhtXoX7CzGQc9gLGbP8UFi3Dnx8FZ2ainSEs8jNnQ//LalYvPGBAQHHUJmWln1mVn1CHt0riAv9SziQ3PhsXwHJo+aDiv9ERimPxzmw8Zi9JiFWLgoAHv89yM7pRThfplYs3QHFi/wxqK5Xpg/zR3jbRxhrG0BQ4PxGDvWHSvdAxCwIwEe7tvhNNwZlrq2GKY3GvZ287F4USCC9xxEbqoQb9xW0asYO9IZxg4RfRBF2VeRlXgWy+eshqXxCJiZT8asmZvh4xmFzWt2Y9miHVi2LBAem+IRsLsICbFnkPXavShC6AiHti4iLjQHm1ZshuPwcdBUNoTGYEPoaRhBW90Q6hoWMDGbCre5foiKPIkdm0LhMGI89I3tYGg0CjbDxsBMzwpqijro11sTgwYYYZjhWEx3XgzXcW4w17eBjoouBvZRQf9+ejAymYplyyOQmnwZ+VmVDXxd1JwxdqQzjB0i+iCKcyqQkXAMcybPgYmuOczMJ2DMqFlwGjEBxpq66N9XFQMUTWBiMRVzF/khKPwIcoQFzQ2u1ylHYWYZspKOYetabzjaOkBTwwSmli5YtGQ3Nm8Ix6pFHhhrPwWa6tYwGjYNXj558FwfCDPDYfi5nyL6qxrBfsx8LHMPxNpV/pjkMB1KfYbip68GQnOwBSaMXY7l7v5Yv9IbrhNmQE/DBH37GcDOcQUi484hN+tqA18XNWeMHekMY4eIPojinFJkJOzFtHGToaWqAU0dE+gbjoCZiQNG2EyGjZUTdDRNMURRG3pGYzB9rjciI45hb/bVBq6mLMROKZIj8+DmPBtDh+hB32AsFq+IQGpaOfYX3EFO8nH4ePjDccwsmFjOxvINKVi93Bem+qb4uc8QaJqMxbL1sUhOv4q9BZUI2B4CS+1h+Olfv0BZ0RqLF4chLeUKCrMvI8w3DlMdZ6DvL1rQMXZBQMRxZHPPDtXB2JHOMHaI6IMozrmM9Pg8uDg6YXC/Pug3eAj0zcZi+lw/BIadQ1rSOezc5Itxw0dDdbAONLVGY5NHEorzrtc79Tw/vQIF6ZcRtTsJYy3HQ6mPHhwdVyAo+AjyhTOuMoVbTlxESkwxtnrFYol7BDZvycOKRdthbmCFwUomGDluOQLDj6Ew7xb2511B5J5YOFiOgGp/DVjbzILPjjxxm1SYWY6EkAIsnrEaQwYYY6jeRPiFHkZWprDguv7fk5ovxo50hrFDRB+EsGcnPb4IrmOd0b9nP/RT1IXjlDXwCz6MrIyr4g+K1OgD8FyxDcONR6HfL/qYMWcnUjPKkJNW+spzCaeG56VeQNC2SNgaO0CxrwkmT/VETLyw2LlcPPRVkF6K3NSLSIk7g4ToM0iOvYDNK31hbWILdU0bTJy0DtGRJ7A39xb25paKsTPWeiS0hujDwWEp/P33idsk4bkSQwqwdNYaKA0whpY+Y4caxtiRzjB2iOiDKM4uR0bCIcx0moYh/ZShom6D2Qt8kZR8CYVZV2te+xcQujMek+xd0e9HdYydsAYRcWeRlXL5lecSYyflAvZsCYO1oQMU+5vBZeY2xCdfQP5LNxEV9ggJp7wL2xZhb8/2tf4YbjoCWtoj4OKyEXERJ7Av50Z17ATEYJz1KOgoG2LcuOUI8N9ffc2d9CtICMnH0plroDzABNqMHXoNxo50hrFDRB9EcVYlMhNPYpHrImip6GOo9ijMW7Qb6Skl4plawmu/MOMSogJS4eowAwN+UMNox+UIiTyJzOQGYif1IoK2R8HWZCwU+w/DlGleiE04/yJ2hNtSZCefR2L4IUQH7kN8+HFsWu4DG9MR0NGxw9SpGxEfydihxsPYkc4wdojogyjMqhQv1rdxmRfM9IdDVX04XGZ4IS7+PArEqxaXIy/lHIJ9YjHRfir6/zgU4503ICr+XL1T0IW9NcKanUj/JDhaT4ByfyOMc1qNoNCjyBWjqQIFGZeQEJaPDUu2YdbE5Vi1PByL53jAytgWOrqMHWp8jB3pDGOHiD6Igkzh7KUSBO+IxbgRE6HYXxvmNjPg5ZOP7KxrOFB4A+mx+7FxqSesjOwxqL8J5i7wR0ZGOXJSX12zI+4FyryCpMh8zJowB9pKxjAzd8GaTYnIyKzAvoLbyEs9jV0eARhl7gANJTNMn+2DBfM8GTv0wTB2pDOMHSL6MNLLxSslZ8QdwPJZy6A9SAMqg40wftJ67NqzD8nxR7Bjow/GjRgDLQ1jGA2bjK1bM1Cc29C9scpQmFWB7KRT8Fi+DXbmI6GuYQ778e7YuacY8bHHscc7DrMmzYO6iimUNUZhtWcKNqz1h5XxcPHmoy4uG+rETjTGWtmLC5SFKyn714mdJcLZWP2MMFTXibFDDWLsSGcYO0T0wQgLhvPTLiJ8VxIWTl4Ac20zDB6gjcFqw6GpZgm1/ppQVtSHufVULF4ZhrjYMyh6zfVsqu+1dRlxQdlYt3QDRljYQVlRF6pDTKCvYQQtVV0oKRtBx2ACps7wQUTECWzbsAdWxjYYOnQ4pkx5NXYi/KPhaGEHrSHCaezLsHv3vpdiJw+LZ6zC4L4G0NRxgm/oIcYO1cPYkc4wdojoAytDduIZRPimYbnbWowwGwNNNXMoK5pAW3U47G3nYcnyEIRFHkeOcKf0eh//6/MIb3OTzyA2KBPrlnjCwXoCdJWNoaWkB92hFrCymQa3ubvg77cfWcklCNmZgvkzVsFl8mqsWRUu3tizOOsqirKuICEsB+5ua+E6fiHclwQgIuxY9dqgtCtIiTqEreuC4TRmEVxcPBAedRLZvDcW1cHYkc4wdojoAxMipRSZiWcRF7IPgTuSsXNTGLasj8BWzxQECHcYjziOTOF0c3FPUN2Pf1V+WgmyE88iIewAQnalY+fmaGzZGAsvz2T47cxFVOgRpCdcRF7qFaTHnkZ08D6EC2dnRR4X72AuXEdHuKGocN+u2JB9iAgoQmz4UWQkXay+B1faFWQnXURS1DGE+hchPPAAMpIuv+bmpNScMXakM4wdIvpdiIe0hHU86aUoSD2HnJSLyE4rF9f2VB/uqv8xr1XzXIUZZcjPKEVWahmyUiuq1wmJ7/v1ujvi5xROT29gHdDr31d7zZ7q99d9H5GAsSOdYewQ0e+kOkKqA6L6rXiNnJrYqf/4N3n5uWqep8Hnqn5crYaeo/7HVHvT+4gEjB3pDGOHPhnVF5YjaajZm0P0nmrXbjUFjB3pDGOHJE/YAApn8OzLvYmD+bdxsOBO9Vsi+nQU3MGB/NvYl3sDhZkVNeFTf3vwe2LsSGcYOyRpwgYvO/kyEiKOIdA3G96b47FlfSw2r42F5xoi+hQIr+ct62Kx3SMegbtykBh1XHzd190e/N4YO9IZxg5JlhA6BenlYuisXOILM5MxGNBXFQP6D4aSkjKUlJWr3xKRdNW8jgcOHIzBg9Qx0tYF3psTkBp35sUNYD8Wxo50hrFDkiXETk5KCfbszIKdzWTIdfsbPvvsf/B1r8+hadUaunZtoG1LRFKlIxjRBhqWrfHjwM8h9+fWUB6sD68N0UiLP4u89Oq1enW3Db8Xxo50hrFDklS7UDEp+iTWrfCHivJQ/OEP/xd/+L9/gInTF9iU3hHexZ2xLb8TEUnU9sJO2JrfCSui28Fy2pf4b88O0NW0QdCuXPEXnbrbhd8bY0c6w9ghSRKudJubegW+29LgNG46Bih9g/Zd/4DPW/4BjovbIbZcARn3/4zU2z2ISKIy7/8ZidcVsDaxE6xcukBJ42c4j12M1JizYmjU3S783hg70hnGDkmScA8j4Wq4yxb4QEd3KNRNu6Gv5p/QttP/gd3stgg9K4/4yh6IuaJARBKVdL0HQs50h+PSVhii81eYDbOBx5qwmm0AY4fz7sPYIckRFyZnVCAu/CgmOS2GosoPMJ/UFhZTWqGz/P+D7Yy2CD3D2CGSslhBWQ9sy+8Co3GtoKj8E6Y6L0FU8H7xEHZTuLI1Y0c6w9ghyRF+o8tMuAiPtWGwMB8BZb2/wHlNWzitaIduf/4jhk9vw9ghkrj4CgXsOdEds7d3gLppd+jo6GL1Mn9kJV+qvijlR1yYXIuxI51h7JDk7M+9gfjw43AetwCauv1hOq4zloV3xNRNHdDtr3+EDWOHSNJiyxSQeK0HPLM6wXR8W6hq/wjHUVOx2ztTDIymcEFBAWNHOsPYIUnJTSsVr5QctKsAOlrDMERHAZPXd8DOfd0wzbMDuv6FsUMkeWUKSLiqgEVBbdFLqQ309AyxYskuJEQeR0GGsFaHscN5v2HskKTkppYiPeE8Vi7xR+/efaBu0Qar4zoiukQBrh4d0LUHY4dI6iIvKyDgmLAwuQX+9W1HjLCejCDfPOSK24Gmc38sxo50hrFDkiEsSBRix2dLCqwtxqPPwH/CZlpb7NzXFYnXe4iHsbowdogkSzh8FVeuIL5+FwW2h5p5a/zS50fMcl2H5OjT4s+MutuFj4mxI51h7JAkVJ+BVY7MxAuYNXUjfv75R2jbdMHcnZ0QfFoO8VcVGDtEEidcHyuuTAG+B7rDyvVLfN9LATbWjuLPC+GkBOEGoHW3DR8TY0c6w9ihJq92MWJGwnkE+WbD3Hgs/vlNRzgsao9ted0QXVq9kWTsEEmXsFdHWKsTdEoeKyK7YLDBl/jxh1+wbMF2xIYeQm5KSZNZmFyLsSOdYexQk1d7PY2YkENYtmAblJXU0Eu5BRYGdEDYeTkkXK2OGsYOkXQJh6+EX1y8crthwopO6D24GzRVzeG/IxO5qU0vdASMHekMY4eaPHGtTlop/L0zMdrOBQOU/w2zSa3hmdFZ3EgKp6gKbxk7RNIVX6mAiItyWBbWCcZjukBJtQ8mj1+KuLAj4uGrpvizgrEjnWHsUBNXvVYnNe4M1q0IhJqKDhT12mNhQCf4H+ku/ibIPTtEElezMNn/aDdMXtcOAzW6YZixLXZsTkRa/Dlxrw737HB+yzB2qEkTQke4u3GwXx5cJi3Gjz3/C52Rn2H3oe7i6ebChlK40qrwlrFDJE1xFQqIvCSPdYmdYT6pPX7q/S9MdFyKzKSLTeY084YwdqQzjB1q0oqzryIt7hzWuPvD0tIKg3XkMWFNC0RclBc3kMKGkrFDJG3CpSP2HOuGKes7QMfy79DR0ceaZUHiDX+bwj2wXoexI51h7FCTJnyPxIQcgfO4hVDR6AWziR2wLqnTizOwhA1lbfQwdoikSbi7+ZacTjAe1xZq2r3gPH4egv0KxJhg7HAaYxg71GTVXkRwx+YkmJnaob+qAiasao3AE3LiMX7xVFXGDpGkCa/jiEvyWBDQHkP0O0BTQwsrF/shPf6cuA1oimt1ajF2pDOMHWqyhO+P2NAjmD19DYbqKkHTsgMWh7St3qNTEzoCxg6RNNVeMdkrtzPs3NphiOa/YWM5Dn7bMmrOwGq6oSNg7EhnGDvUJAkbuf15N+GzOQXGhlbQMPoXHBZ1wPaCLuKp5rV7dQSMHSKJqokdN5/WGKzXEQZGOljg5oH48GPier2624WmhrEjnWHsUJMkxM6+3BtYNt8PP/f8AXr2bbEyuqN4xoawcXx5g8nYIZIqeURdVoDt7D/hq//KYezomQjYmYWc1NImvVanFmNHOsPYoSal9noa2cmXERG4Hw72s/Bj7z/DdlYr7NzXBQlX624sGTtEUlO7Zzb0rBw2pXWBpvWX+P77HzB/1hYkRZ9CYVZlvW1DU8TYkc4wdqhJqY2dlJjTmD9zK1RV1aAxrDtmenVA0MlujB2iT4Cw7k44o3JHcVeMXtga/VTlYWxkhc3rIpCZKNzwk7HDadxh7FCTIoROTsplhO8phrmRE77/pQdGzu2EDcldxGvr1F5T52WMHSJpEWIn7Lw81sR1whCjz9G33y9wm7kGof6F4hmYBRlN6+7mr8PYkc4wdqjJqD3zIjn6BLZsiIDiQE38MPBzzPfrhIBjctUbyZcWJtdi7BBJR/VeHXn4HuiOmVs74bu+baCubIqdW5PE28K8vC1o6hg70hnGDjUZhRkV4q0hgvzyMGOqO3r3+wHq1n+CZ2YX8dYQdRcm12LsEEmHcMPP8AtyWBPfBSNmdkHPPv+LUTYzkRB5HPlpTfMeWK/D2JHOMHaoySjOuors5BJsXBMGraEG6KfWGRNXt4Hfoe4vrsdRd8MpYOwQSUfSjR4IPt0dLhvbY4iuHDQ1dLFykR8yEy80+YsI1sXYkc4wdqhJqF2YHBV8ANMmr8C3P3wFvdGfY0tWV4Sekxc3kg0dwhIwdoikQXgNCzyzOsPMuQ1+6v0VnBwWIjr4ALKTL73YDtTdPjRVjB3pDGOHmoSirEqkxp7BhlVBsDK3R88B3TFxTUtEiXc2r46d12HsEEmDcDZlwNFumL6lAzTNu0FZRQXrVoSKN/zMSyutt11o6hg70hnGDjUJwvdCVPBBuE5eBm39IdC26Qj3iPbixvF1e3RqMXaImj7hdSzc3dwzszOsXTtC0+AHjBg+AYE787A/92a9bYIUMHakM4wd+uiqd12XY8eWZFhZjIaq3r8wdlkH+OztiviKHq/cB6shjB0iCShTQPQVBSwIaAcN8y4wMNbB4rleSIw8ieKsa/W2C1LA2JHOMHboo8pPr767eVL0SSycswXqGipQH9YBy8I7ioew3rZXR8DYIWrihNdxqTx2HegmXkRwgMpfMdx6HHZ7ZyIvrUwSt4ZoCGNHOsPYoY9K2MgJ3wc+W1JgY+0AJa3/wGpqG3gXdxHP2mDsEEmf8BqNLpHHAv/20LTsBDUNRcxwWY2EyBMozr5eb7sgFYwd6Qxjhz4q4Uqpwt2N583cioGKfaFv3xVzfTsi5IwcEq++W6wwdoiasDIF8crnYefkYD39T+jV/28YZTcRWzdFS+rWEA1h7EhnGDv0UQmXhk+JOYVRtm74sc9fMWpee2wr6CpuJF93XZ26GDtETVvkZXlsL+gKZfM/omfPn7FozmbEhR0WtwFSOtW8LsaOdIaxQx/Fyzf83LQ6DLo6plDU7oyZW9uJFxwTrrJad4P5Oowdoqap9heWXQe6Y7pXB/RT74ChGsbw2hiDrKRLkl2rU4uxI51h7NBHUf3bXClCdxfC3mYaBip/C8vJHcUbA0ZelmPsEH0ChNemcAPfVTGdoG3XCoOUf4Lz+AUI2Z0vbgcYO5zfaxg79FEIsZOecA6b10Wh908q6K3aGnN2dhJvDSFsJIWbBdbdcL4OY4eoCRJOLihTQMCx7nDZ1BZf/fgldLUssG1TDJJjTopnYUn5EJaAsSOdYezQ7074bU644WdEYDHcpq/DV1/9C2pW/w9euV3FY/viGVjvcBZWLcYOUdNTu1fHI70Lhs9oh3/8Sx5jbOchMeqEuFZPiJ262wapYexIZxg79LsrzKxAevw5eKwNh5XlSPRRkseYxS0QcFxO3KPzLqeb192oCm8ZO0RNhHAGVqWwV6cbZm3rAF0beSgNUcGy+buQnVLyyWz3GTvSGcYO/a7y08rE2IkNPSze8LPfwJ+hP7odlkd2FG/4KR6+YuwQSZrwC4vwutyc3RmWLm0wSOVrjB01AwE+2chNK5X84atajB3pDGOHfjfCBq4gvRyZiRewY0sibKwc8GP/LpiwqjX8j3ZH5OX6G813wdghajpia2In5Iw8FgR0hKZFZygpqWLNsj1Iiz8nyRt+vg5jRzrD2KHfjRA7wl6dqKCDmDd7I3T11aFs3BbLI9uLe3SE++bU3XC+C8YOUdMhnG4u2JLdBQ6LOkJN/z+wHOaAEN8C8QKijB3OxxjGDv1uhH/roqyr8NmcguFWjlDR+TdsZ7SFd1Fn8W7I73v46sXGlbFD1GQIr0fhl5eFAe2gM7wLtPVUMNNlFZKjTmFf7o162wUpY+xIZxg79DupPoQlXEhs2XwfqKiqQM20A+b7dkDIabnqu5s3sOF8F4wdoqZDCB3hNe24tBX6q/wFluYjxVtDZCdfkvStIRrC2JHOMHbodyHcA0t4u2dnNsbYu6LvoK9hPqkVfA92Q8JvjBLGDlHTIBy+Ek43XxPbCTp2rdF/0E+YPmWleKX06tD5NBYm12LsSGcYO/S7EP6thWtrLJm3HTo6Q6E5TB7TPNsj8pJ89SGsBjac74qxQ9QElCkg8VoPBJ7sBofFrTFE+68YZmqNTWvCxPV6RZnCep362wYpY+xIZxg79LsQNgrJ0acwavh0KKr8B/azO2FjShdElQix8tuihLFD1DQIr2WvvM5Qs/gCSqr9MHvaSoT6F4rbAOEwdt3tgtQxdqQzjB36XaQnnIe3ZwJ0hg7DoKFdMX1LB/Ey8sJvg+97EcG6GDtEH5fwGo4uVcCeE3KY49sevZTaQFvLGB5rwpAad+aTuDVEQxg70hnGDn1QtRu4UP8iTJmwBINVekN/VDusjO5YfWuI97gH1uswdog+LuF1HHFJHuuShIsItkXfQV9h1AhXBPnmvbId+NQwdqQzjB36oISNnHAfLM81kVBR0oGSrjwmrekA7+Ku4m+Dv3WvjuCdY6fm89VV9/mI6D0Ir6NyBQSdloPLpjbordwBejqGWL7IB4mRx8V74TF2OB97GDv0wQgbOGFRclL0Ccyeuh7/+MffoD+6BTaldUX4+ZobftbdcMrgXWJH2BgnXOuB5Fs9kHqnxq0eSLreA/HCdUEa6WshalZqfmGIKpGHd2E3mDm3wN//Vx6Txi5CZOBeZCdf/mRDR8DYkc4wduiDEX6jy0g4Bx+vJAy3Got/ftMOoxd9icATcuIpqo0VGK+Nnas9qvfeXFFA5AV57CzoipUhnTHPuxNmb++I+QGdsT6jGwJOyYvrDWS5CSlRs1ZzteQ9x7tjcWBnqJm2x3f/7YWViwPEPbqf+vadsSOdYezQByHeByujHDEhhzBr6hqoqA2C6rC2mL+7PcLOyYsbyHobThm9MXauKCD0pBw2RXfGxPltoGfRAooaX6KfxpdQNGkJ40ltMdu3M3Ydkqu+Nxdjh+id1f6CsDmzC+zc2kNR418YZjwKO71Sa7YDn/b2nbEjnWHs0AchxI6wC3vX1lSYGY9Bz4HyGOfeDtvzuyBKWJjciFHRYOycrT6MFX5WHpsTusB+fGtoGbaA8djWsJnVBnZz28Jychso67aAnm1rLAisDp4oYQ/PO35tddf+NLgGqIH31/Wm56v7OYmaCvF7tFwBYeeFG352gKppO6ioKmPp/O2IDz+K/E94YXItxo50hrFDja72ehpx4Ufgvsgbqqqq6K/9BVbFdUDERbl6G83fqqHYEfYeCRtiv73dMGdTe/Qf8DkUtVpgytaOWJfdDVsLumJFcCfom7RAn4FfwH5he6wT1hJdlBfX8NT9HHXVbuiFt9HCmoU6sfLK41720scIXnmf8HcpFVTv+ar7XERNSfXrTh7eRd0w3r0D+qv+BcOMHcQzL4W1enW3C58ixo50hrFDja4wowI5KaXw2ZKEcQ5Toaz9DcyntIDvoS5IuNr4p4M3GDvn5RFdooAtKV3gNK8tfhnyJYyntIVHUXeECxFRoYCAQ93h5NYGg9S/gOHENlgU1gWh5+SRUFn/c9QlXPlZWGQdfFoO/sfl4HtMHoGn5RF+QV68UKKwBkj4/MKl84U/C7+oIL4NOyuHoFNy2H1CDnuEx18UFncKz6eAsNPyCDksh5BD3REiPpcCIkuEzydf7/MTfWzintOL8lgc2BHDxspBQ2sQpk9eg4zEi+INf+tuFz5FjB3pDGOHGl1RViWyki5jyVxvaGioQ8O8K9x2dUDYObnffB+shjQYO8KenSsK8N3bHStCO2Pq5o5YkdgVYSUKSLjRA8k3e4iH02atbwdVgy+hP74N5gd1QcjZN8dOfKUC4srksSW1C6atbAfrca1gYNsSeqNbw3RqW7j6dMK2/d0RckYeuw90x+qIzpjn3wkL9nTGHK8OGDu7DUxGtYTWiNawcmuPheFdsHNfN2yI7YxJi9timF1L6Fi2gumktpi5qzO2FXcXI0n4u9T9Wog+JuE2L0Gnu2P0wlYYPPTvsLYYCa8NMchLrd4G1N0ufIoYO9IZxg41qtprakQG7cf4MXPQe8C/MWxiS3jldUF0iTziPsBhmYZi58Wp58Lne+kQUkypAiLOyyPoeHdszewMO5dWGKzfAraL2mFVUjeEve4wVs3zRF6Uw468zhi/oA0UVb/Af7/5DP/572f4+qfP8L8/f47+pq0wcXNHbMrqhvXxXeA4pw1UbVpC1bYldKxaYKDy5/j3159B/q+f4a/ffQFV61aYsrodxs1tA3WDL/HNj59B7i//g65/+wyDzFrBdUcn7Dws1yhXmiZqLLXfi56ZnaE3qpV4w8+pE5YhJuTgJ3u15IYwdqQzjB1qVMK/aXrceaxc4gtjY1Mo68nDZaOwp6XmdPMGNpy/1ZtipzZyhMfElcsj+GR3bErojNke7THCpRV6q34hRsWMPZ2x43D1AuWGgqz6Ss9y2JbZGWPdWkPNrAWGjmoNx1XtMX9PRyzw7QDHuW0w2LAF1Ee2hqtvJywO6wz7GW3w3yGf49+qX8B4ahs4e3TEDO+OmODeDkpDW+B///4nKKq3gNWUtpji0QHzd3fA5JXtoGnWAj8pfQmjqW2xKrMbwoX/dh/ovx/R+0q4qgD/I90weV17qBoqwEDPBOtXBCO7GZxu/jLGjnSGsUONan/eTcSFHcPYUTOhpt0L5hM6Y2VMx+rgaMTTzV/2ptipfYz4m2ipHHyKumC6R3uYjm2JIdqf439/+hP6mbfC7NDO2HVMDtHC8zUQOzFl8og43x1LfDtARfMLDDZuAYf1HbAxvxtCL8kj9Gx3bEntDLtZbaDr1AbO2zphjn8njJjWGv/q/Sd8M/QLTNzeCZ57uyPgjDy887rAanRL/LXb/6CP0pdwXNYBm3K7IfSCHHYWdoWLe1v8ovwlhti0wvzYLgiuPc237tdF9DsTXkvCxTg9MztBb1QbqGn/ggnj3LBnZy4KMyuazV4dAWNHOsPYoUZUKr74/bZnQFfLFCr6PeCyvgN2HejWqBcRrOtdYyf6shy253WBi0d7mE1qDW3rFuil9gX6m7SE47oO2JDVHWEXG4gy4WNL5BF0tJsYId98/Sdo2bfGkoQu2CNcM0hYxyPcG+i8HFZEdYbL9k6YH9oF8/w6YcTU1vhv3z9hoE1LrMjoihDh1ParCgg93Q0O01vhP//6H2jatILb7s7Yc0q4NpCwULk7VgR0wCCtFhho2gpu4Z0RWMLYoSaitNoC/7bordIOhoamWO2+G4lRJ1GQUSEexqq/bfg0MXakM4wdajS5aaWICz+K+bM8MWBgH+iOaI/VMR3Fs5I+VOgI3jl2ShQQeLw7PLO6YmVMFywO6ASH+W2hbNISKjatMXl7J+w8LoeYuguUhVPLL8nDr7grxsxog7/+9U8wmdIWnvu7I7zmujziaePC/YFOyWHnITns2CeHlRGdMXJaa/w45Atoj2+Drfu6I6ZCAfFXhT1B3TB+Tmv89ONnGDalLZbFdkXo+eq/S/gZOayP6AQlvRYYZNwKbmGdEXiZsUNNQ8QFBWwv6Ab7Oa3wfa8eGGM/DcF++eLC5OrQYexwmt4wdqhRCAuThdjxWBMFA10LDFT7K0YvaI+d+7oi8Vr12pm6G83G8qbYEd4n3BNL2O0unGUlBINwRpVwCrwQP15pXWDh2Arf9/8CZjPbYl1eN0Q0cK2cyIvy2JnXFfYubfDnv/0JZrPaYdsxOUTWeazwvMJ9t+LLFbA5pQtGz2qDnupfwnByW/js7S4+Nr5SHiFnqmOn58+fwWJaWyxP6IoQIXbKq2NnXXgnKOm2wCCTlowdahKE713h+zP4lDymb2kHRZ32UFIegoVuXkiJOYPiZnK6+csYO9IZxg79ZrW3hshKuggXp1X493/+AYPR7bE0tDNCTsu9iJEP5XWxE1fRQ7wejnA1ZeGU8ohLv26wxUNVwplZp7tjypK26NnnCxiObwP3xK4IvfzqoSzhY6IuymNXQVeMnt4Gf/3HnzBsZjtsPSqHiJfOTBEfd7k6jIS/9/q4Lhg1ow16aXwJI5e22FEbOxV1Yse1LZbHM3aoaRPX3ZUpwPdAdxiO/RO++s9fMHb0DOzaloqspEs1h7Dqbx8+ZYwd6Qxjh36T6sWIZchMvIAw/wKYGY3HX//VGk4r28L3YHcxKD7kXh1BQ7ETfk5evI7OZuF6OBvbY+Si9lgc3qX6vlzCXc7Lqw9rhZ/qjkmL2+Dnvl+K98laldEN4XUXKYvrfeSx51A3TJzfFv/63z/BaEJbbMjvjrBL1Vc7jqsQ3spjQ3RnTFvdHm7enTDDq6O4ZqePFmOHpE18DZcpIOSMHNbEdkF/7c/w3//0xNrle5ASc+qlQ1j1txGfMsaOdIaxQ7+JeF2dtDLEhh3G8kU7oKKigV5KLbAoULg1xGuuWdPIGoyd8/LiOpt10Z1hO7kVflT8EsOmtsPWou7iGVfCIa3I83LwjO8Ec4eW6KX8JUYsbI8te7sjWoihup+ntHrh8FyP9ujT53NoWLfCLOF+WiflEHet+rT2wCNdMX5eG2gMawm7Be0waWMHjHBtw9ghyRO+L4Wrgm/N6wbnVZ3Qe3AXaKiYYc/OnOo9u810O87Ykc4wdug3EWInJ6UEft7pGGE9Ef2V/wmrqW3hmdlF3Dh+6ENYgoZiR7jtg3jfnpyumOLeDj/98gUG6raE6/ZO2JjRDd4F3bAxvhPGz20NZYMvoWnfCjN2dcLuk/KIrbtAufYQ1SV5bIjpDIsxLaFi1gIWc9phfkQXeBV1g1d2FyzwaQ9t65YYPKwVxm3sgNm7O4nX2REOYxlOqR8749yqFyibT20L97g6sRPWCUO0W2CgUUvxtHjGDn1Mwi8t4RfksES4n5xdZyip9IfLxOWIDTsibgMYO4ydpj6MHZKZ8BudIDnmFNYu94eykhoG67fGkpDO2HO8uxg7H/oQlqDB2BHvei6c4i2H9TFdYOnQCoM1v4SGZUsYjm8NU+fWMBjZEkr6X0LDrhUmbOmATfndEF5zWKru56j9ewQc7oalAR1gOakV1C1aQNu+FYY5tYa5U0toWLXAELOWsJ7fHktju2BFTGdxgXIvYYFyA7Ez3q01fv6pOnbq7dkRYkenBQYat8Rs7tmhj0j4nhX4HeoG5zXt0V9FHuYmo7FraxrS48+/2A7U3T40B4wd6Qxjh2RWu1cn0DcHrpMXoVffr2Hg+Bn8j3avt8H8kBqMnTPy4plRwkY6+JQc1kZ0xGjX1lDR+xK/qH2BH5W/QE/lL6E2vBUmenUUTyMPuVxza4kGPket2DJ5hJ7ujiW7O8JybEsM1vgCvQd9jj4qn6O/YQtYzWmPFQld4XtEDluzu2L6hvYwGt8aY1d3FP9M+HqErzfsfHe4bWoPA6uWmLC2AzZmVt+qQrxezzk5bEnuAivnNjBzbQv35K4IKZFHDGOHPgJhr46w0H9tQhdYTemEPv2/hYvTSmQnX26W63RextiRzjB2SGbirSHiz2PVst0wM7fEAA15jF/RUlyrI1xor+5G80N5XeyIp56LV05WQPg5Ofju64ZNiV2wMqwzlod0xqrYrvDI6Ybdx+UQLtxdvGYRZt3nf1ntlaBDTgr3yOqKDYld4B7ZGUsiu2BtSlf47JdDqLBeSFj8fE4e/oe7i9ckERZrC2eDic9Tc5HCgMNy2JbTDb7Cnc7PyYt7woT3Cwunw87IY0dRd3gXyyHwjDyiGvhaiH4PwmUb9hzrhsnrO2Co+V+gNVQHq5bsQXH2VfEXnrrbheaEsSOdYeyQzISNXXTwITg5zMVA5R9hMq4d1iV2En9YN3Qo6EN5U+wIfy5e8K+i+i7NSdd6IEE4lFRW8/9v1Fx/5y17dF4hHooSfggoIPFmD8Re64Goih5IuN5DvKaQeLZXzSnuwj2EhM8jvK17SE/4+hKFz3+1x6v/vcS9Pz3Ej6t9vnpfA9HvRPge9MzsCIMxrTFE/SdMHDsHIX6F4q0hGDuMHakMY4dkImzohOvqbF4XCWMjS/RTE37za4XQs3LvHg2N5G2x87IXX1vNXpTf9LXW7AkSzu4S1Hv/y4+r+2fv8j6ij0h4bQh7MkPOdMcs73YYrNMFWlr6WLc8SLyuTnNdp/Myxo50hrFDMtmbcx2Rew5gktN8aOr2h/7IDlgZ3b76TuMNbDg/pPeJHSJ6N+Ji+koFbEjtCPNJ7aGq/SNGj3RF4M5cFGVVMnYYO5Iaxg7JRIidbRsToadjCk2Tf2DCig7w2dv1xaLguhvOD4mxQ/QBCId2yxUwY3srDBzaGabDTLBs4XYkRp5AUTO8NURDGDvSGcYOvbfclBLxTIzFc7zRr/8vMBzdCSsiOyH8QvXViettND8wxg5R4xOuQC7c2HaE2xf4vudfMM5xJvx3ZIhnYDbHW0M0hLEjnWHs0DurvZ5GVuIF+G1Ph531JPQZ/HeMmtdOvOGnsFen7gbz98DYIWo8tXtmA0/KwT28E9QtWqFvvz5YPNcLSVEnxfV6dbcNzRVjRzrD2KF3JoSOsKFLjz+H6ZPXYsDAvtAd3hXzdnUUFyYLZ23U3XD+Hhg7RI1HPJuwXAE+e7vByrUFeg36C6wtHeDtES/u0RXW69TdNjRXjB3pDGOH3ln1gsRSRIcchJGOA77+oQOc3DtiS3ZXcZf373m6+csYO0SNR3g9RV5WwPrEzuir+Uf80qs/3BdtR1TwAeSmljb7081fxtiRzjB26J3UnnmREHkMm9aEYEBfdfww8E9YHNRJvEJx7SXl6244fw+MHaLGIezRES5uuXNfd0zz7Ij/9mwJDSUz+PtkITPxgnjFZJ6F9SvGjnSGsUPvRDh8JSxM3O2dDifHWejZ92tojfgCm7Nqbvj5kfbqCBg7RI1DWHcXdl4OyyM6w3xiZ/zc+yuMGeGGhMjjzfoeWK/D2JHOMHbonQjH6YVbQ6xetlu84edA7faY5tlevB3Cx9yrI2DsEDUC4ari13og4Fg3TFzdHgPVe0BfxwwbVoYgI+F8zeErxs7LGDvSGcYOvVXtb3PhAcVwcV6Cb3/8B0ydP8eu/d0RcUG+/kbzd8bYIfrtqg9hyWNTameYObdDz97fYPrkNUiNOY2clMvITxe2B4ydlzF2pDOMHXor4R5YqXFnsW5FICwsRqCnYhe4eLRAwrWPe/iqFmOH6LdLvKoA/6PdMM2zA7Qs5KGqqoHN62JxMP92vW0CVWPsSGcYO/RWe3OuIXLPPkx2WggNnQHQteuAFdHtG7y55cfA2CH6bYTXsXCT3I1pwq0hOkBD7yeMHDEJQbvysT/3Zr1tAlVj7EhnGDv0RsK/j7Aw2Wt9NEyNbTBE+6+YsKo9dh3oVr1Xh7FDJGniLyxlCoi4KI9Z3m2hbNgV+gZ6cF+0A0nRp3hriDdg7EhnGDv0WsJanYKMSsSGHcGcaeugpjkYmlbtsTKmY/V9c5pA6AgYO0SyE9bqxFyRx7aCLhgxuw0Gqv4LdsMnYs/OXHH7zG306zF2pDOMHXotIXaE3+p8tqRghM04aBh8gxGz2sJnXxck3Wg6IcHYIZJdbIUCokvksSCgPbSHd4GWripmu65DUtQpcRtdd7tAv2LsSGcYO/Ra1Xt2KrBwtjeUlAfDeLQC5vt1RMiZ7h/tPlgNYewQyU7YsxN2Vg62bp+jr9LfMGbURGzdGIPMxIviD/O62wX6FWNHOsPYodfKTilBfPgR2Fm54vteCrCf2xbbC7q+2EDW3Wh+LIwdIhnUHIYOvyCPLdldMMT4j/jpp55YOGcz4sKPiNsAbp/fjLEjnWHsUD21V0pNjDoB9wU+0NDUgrJhJ8zybo/g03KIr4mLpoKxQ/T+hBMMhKufexd2hdOKduir3B36Otbw2hiLzKSLvAfWO2DsSGcYO1RPdexcQah/ISyMx6PfkH/B3q0TNqR0EW/4ydghkr74ih6IvKSA5VEdoGTyJQYr9cXMqSsRFlAkbgcYO2/H2JHOMHaoQRkJ58R/o3691dBfoy3m+3XB7sPdxY1kU7iQ4MsYO0TvSTib8ooC9hyXw7Qt7fB1z5bQ17GCt2c8UmJO1VwpmVdLfhvGjnSGsUOvKEgvR3byZYT452Om60p8/8N/oW37BbZkdROvw9GUTjmvxdghej/Ca0a44ef65K4YPr0Dvv72L3C0n4v4iKPISS5h6Lwjxo50hrFDryjMqEBq7BmscfeHob4p+ip3w7jlrRFwrLu4KLmphY6AsUP0HsoUxNeG76FumLy+PdSM5aGirIHlC/2QnXypZpvM2HkXjB3pDGOHXqg91Twq6AAmjluI73/+J0zGt8L65M4IOy9ffQYWY4dI0oRfWIRD0ZvSOsHIsTV69/8Gk50WI9S/GHmppS9u/Etvx9iRzjB2SFQdOuXISLiA7Z5xsDAfiW97t8eUTa0QelYOUSX1N5pNBWOH6N0IoSP80iKcVTnfrwPUTDphiKIaPNdGIye1tN52gd6MsSOdYeyQSPh3KMqqRGTQAbhNXwNtPRWomLbFqpgO4g0/6240mxLGDtG7EfboxFcqwDOzM0bO7Qg1vf/A2nwcwgP2YV/OjXrbBXozxo50hrFDIuHfQdizs80jAZbm9lDW/V+MnN8OPsVdkXitR5M8fFWLsUP0bmpfK3N2tYOGeTfo6mti3syNSIk5jb051+ttF+jNGDvSGcYOvbiIYFL0Scyb6QElVUVoWrXDsvCOCD8v3+RONa+LsUP0drUnF/ge6g67OW3QX+kfsBs+Ab7b0pCTUoLCzIp62wZ6M8aOdIaxQy82cj5bkjDCxgkDVL6CzYxWCDjWrXqvTgMbzqaEsUP0dsLrQfjlZXFQJwy1bo8hyv0xZ/pGpMef5z2wZMTYkc4wdkj8d8hNvYKFbl4Yqq0OHWs5zNzWHpGX5JF4vekHA2OH6C3KFJB0vQeCTnbHqPmtMUTrf2FlaY/N66PEvbpFjB2ZMHakM4wdEtfqxIUfg72NKwaq/Buj5naCR3pX8QysuIqmHwyMHaJ3UKaAzVmdoGb+BZRUB2DOzLUI31NcvQ3gdlgmjB3pDGOnmRN+q0uNPY1Na8IwdKgBhuh1wSzvDgg8KVd9mmoTXphci7FD9HrCazi6RAF+h7pjuld7/DKkIwz0zMVtcHrC+Rdr9upuG+jtGDvSGcZOM1a7kQv2K8D4MW5Q0ewJs4kdsDahE6JKai4i2MDGs6mpFzsz2iDsrDwSrvZ4EWzvqimfdUYkC+EEA+FWL6tiOsJ0fHsMVvkJE8fNR6h/9Q0/GTqyY+xIZxg7zZiwkctOLsGm1ZFQVtSCqrE8pm/uiF37u0lmr46gbuwMn9EG4efkxcXVwob+fUjl70z0TmovInhKDpM3tEZPxfYwNbLA+pVBSI4+KW5/GTuyY+xIZxg7zZSwgctNLUVS1AnMdt2Iv//979C2/xIbUrqIZ2xI6Yd+3dixdGmDgKNyiLosL97m4l2FX5BH5KXqXf51PweR5NT8whJ1WQHeRd1gNukL9PhLF4wfPQ8Re/aKN/zl9ve3YexIZxg7zZSwKDkt7iy2bYqBpfkYfPV9e4yc/yX8j3SX1F4dQW3sTN/SER27/z/87/efQdOmJXRHtoSO3dtpj6h+rLDWZ/b2jvA90F28ymzdz0MkKcKeynIF+B/tjvl+HaFq0h7ffdMLy+btQmbixZrD2PW3DfTuGDvSGcZOMyRs5IQXaXTIIUxxWoKBg3tC164dloV2QPj56sM59TacTVht7Mzc2hEduv0/tGz7f/HX//wP/v7N/+Dv//3snfz5q//BX/7zP1A2bYE1cV2QfLN6vU/dz0UkFeJh2QoFeGR0huWUthik8jXsbCbB3zvzxXag7raB3g9jRzrD2GmGag9h+W1Pg7H+CPzQtz1cPdrB71A38XRzqf2Qr40dV88O6Cz/RygZt4Dbjo5YFNgJC/zfblloZ7hs7ABFgxbor/UlFgd1Rsotxg5JW+3C5IV7OmCwQTuoKGtg46pQ8dYQtduButsGej+MHekMY6eZqf3vHRd2GO4Lt0NZWRn9hn6OdYkdEV1af4MpBXXX7Fi7tkHQSXnxz4Q1OKLL1WsXhLei2j+/pCAuZPYu6g6DMa3Qb+gXWLC7E1JuM3ZIuqpfE/LwLuyG8e4d0Fe5B4YZOSA66CC3uY2IsSOdYew0MwUZFeJ9cLw9EzBm5CQMVv8awya2wK4DXcVTtaV46nXd2LGd1QYRFxSQfPPP4rV2hL+XEDTC1aDFt9eq/0xU2QMZ9/8sXoPEeBxjhz4NCZUKCD8vh4UBHWE0pitUNPphqvMKca1OUda1etsFkg1jRzrD2GlmijIrkB5/Dgtmb4aqmjI0zDth7q4OCD0rJ/7g/xRip6GLCgrhIq5hqDm9/OWQEQ5Z7dzXHUaOjB36NAixE3C0G0bOaw1FjX/A2mIUtm6MEW8Lw/tgNR7GjnSGsdOMCGdgCW9DdhfAcdQ09FX8J6ynt8DO/d3EDaRUf7i/LnaEPTdC4IScES6o1kVcwDx3V0esTegC34PdxcNZQvwwduhTInxPC5ddWJ/UGbr27aA4pB9mT10vXmaC19VpXIwd6QxjpxkR/nunxZ+H+yIfGJsYQd1EuOFnW0SXyiO+Jhik6HWxIxyuir6iAM/MblCzaIEuf/4j/vHt/4inm8/d1QnBp6uDiLFDnxLhe3r34W6YuKo91I3/DlMTK2xeFy3e/6r2Fx5qHIwd6QxjpxnZn3cLcaFHMWrEVKho/QDLSZ3EW0PUXj247kZTKhqMnbPCYazqK8cuCuiEf//8Gf7whz/g8xb/B9/1+xwOi9uJFx5MusHYoU9ImQKSb/SAZ3onaNm0hppWX0yeMB/Bvvninc25V6dxMXakM4ydZiI3rVS0bVM8NDX0oWzQHa6bOogLc+uuYZGa18dODwSdksOSoM7oqfQ5Wrb+v+ja448YoPMlJq1rj8DjcuLeH8YOfRKEqyWXCAuT5TF7R1v0HNwBRoZmWLdyj3hriOo7mzN2GhNjRzrD2GkGhKukCqETvmcvpk5aJl5E0MihHdYldhJPN5f6D/XXxY6wO184tXxLdjfxdPTeal9AxbSFuFdHWLcj/FCIq2Ds0KdB+H4Vvqc3pnaB5ZQ26NnvnxjnMBth/kUv7dFh7DQmxo50hrHTDAj/jYWzMDasDIXWUEOoGPwFzqvbw/dQVyRck/4P9QZjp2aBsvB3ExYor03sAjefjlgY0Ambs7qJh7dqQ4+xQ1InfK8Kh6KDTwo3/GyDgUM7Q1dXD8sX70Rq7FkUZV2tt12g346xI51h7Hzyqn+TS48/CxenVfjmu3/BfGJHrInpLJ5uXhsKUva62Hn51HOBeNHEBi6cyNghqRO+V4Xvb5+93aE/9jN8/f3fMcV5IfbszEJW0iUuTP5AGDvSGcbOJ6x613UZ0uLPIcAnE6aGDvjHf9pgwqq22H1Yrvq3wYqaa89IWPzV6reuHtWxM3xGG4Sdk6/ea1Wz+Fq4hpB4McFrPcSFyy+uuVOugNQ7PbBrf3cYj22FflpfYKF/J6Te7fFJ/LehT1/t92nQSTm4h3dGH83P8N+ve2LtikCkxNbcGoKHrz4Ixo50hrHzCav9bS4yaD/mzlwPFbXBUDJqBffwjuJvg8m3eohnI0mdsBdGeDvDqyO6/vmPGDG7DaIvCxHz53qPbUjWoz/D/6gcTMe3wgDtL7AkuDOyHv9ZvBlo3ccSNTWpt4WQV4BXTleMWdgRvRX/DL2httjtnSn+IOYZWB8OY0c6w9j5hBVmVohvfbdV3/Dzn//thCEmn2HimhZYEtoWyyPbwT1C+pZHVb8d5vwFWnX4A1QtPsPCPW2xIrr+YxuyJqE9Zm5vgwG6f8R/fvk/GOH2pfhnn8p/H/q0Cd/nwuvZYXFLDNHrCI2h6lgwewviwo6Ie3YZOx8OY0c6w9j5hNXGzo7NCVBTNkDHLi3x1Q9t0FetPYbod4SSQUfxrdTV/j2+690W7Tq0wFfftYGiTkcoGXao99iGqBh3RH/NDvjH160h/9dW+HFAO/HPPpX/PvRpUzLsiMF67fHLkM7o1edrOI6ZhtDdBchKusjY+cAYO9IZxs4n7MXtIfzyMGHsPGioGUNnqDl0tSyI6JNiDgPd4bAbPgUea8OQk3JZvORE3W0CNS7GjnSGsdMMCL/hJUQeR1TwAUQFH0Rk4KcpKugQYkIPITr4UL33vdGe6rfCx0WHHEJU0K9/RiQVUcGHEB9+DBkJ58W9OYydD4+xI51h7DQDwh6efbk3cLDgNg7mE9Gn6ED+bezPvYmiLN7V/PfC2JHOMHaIiIhkwNiRzjB2iIiIZMDYkc4wdoiIiGTA2JHOMHaIiIhkwNiRzjB2iIiIZNCYsfP82XNUVVXhaVUVnj9/XvfdL+b582eoqnqKp0+f4smTJ3j85AmePH2KqqpnePaGj2vuw9ghIiKSQePFzlOUXTyLlPgUxCVkoPT6LTyr+xA8B6oeoPTcESSE+2PzOncsmD8PbouWY9UmH8SmFKDk6h08rmLwNDSMHSIiIhk0Suw8f4qyC8cQsG0TRts4wGnyAhSdu4SnrzyoCo/uX8PFE/kI2L4aTqOsYKKnATU1FQxW14G6rjnGOM+FT1gyjl8sw8Oqqlc+msPYISIikonssfMcz549xaP7d3Dx5CEEbluHEaaG6NtbCcMdZ6Dw/GW8nCtVVbdx/kwhvNbOw2g7a4ybMg1rN29DYGgIggN9sW7FAtjZ2cHMbiJ8wuNw8frNVz6ew9ghIiKSiWyxU4WqqjuouHIGOSnx2Lh0KSaOGgENNWX82EsRVo7TUXT+8kuHsZ7hwd0ryMuMwBgrMxgZW2Hj7hAUHD2N8uvXcL38Ag4XJ2CR2ySoKmlgrvs6FB47jftPXt039LZ5/vQ5nj1+Jh4te5cRlgc9fQo8q3e8TXiCp3iOp2JwvePTffBh7BAREclAtth5gocPSrA3LxbL3GZh2FBTWJlbwczWEorqBrAZNxOF5y79GjvPq3Dn2iVkxIdgpPlwOLvOR+GZ87jx8PGL53vy8ArCd6+H/pDBmDR5JuIy8nHjzv1fP2UD8xzP8PD+XVSWleDsyRM4vP8g9hcfxOFDx3Hu/GVcv3kbj588xbOnT3D/3h2UlF7B5culuHn9KkovX8DRo0ewt/ggDh48joslV3DnwX3cvncbZaUXcPbUfhw6UoS9R4/j5IUS3Lh1R1x4/TGHsUNERCQD2WLnEe7ePoeYkJ1wsnfGpIkLsMnDC+7LF8PE3A7Dx89CwdmLL8XOMzy6XYnzhwsRumsnYlLTUfb4MZ68eD5h38k9pMXugJnKEEwc74KIxExcvXn3xSMamqqqBzh7fC/2bNuA6RMdYGNlDiNzS5hYjIHr7JWITspBWcU13Lt9DccPF2PjRi+sXu2B5OhgeKxcAAdbCxjrG8LCagwWrdmCnGNHkLcvF94eK+E61hZmhvowMLGD69xViE/Lw7Vbdz7qXh7GDhERkQxki50nuH+/AvlZmdi1LQTZ+Udx+tQJhPh6Y/hwBwwfNwv5r8TOc+DJIzy7fwP3b1zBzXs3cee5cJCo9v1VeHC/BH7bVkK1/2A4T52H5Px9uHX/4YvPWHeePH6AkvPHsGXdClgbG0Nfayj0jPShZ2aKoVpGUB6si3HjZiA+MR2njh9CckwwTI2s8UsvdUyZ4IQJjqNgZaoPHbXB6N3zFwxUGYppq5dgmcdKTHNxxihLc+iqqaPvzwPRq6caXGa6o/joKdx//Gui/d7D2CEiIpKBbLHzHM+eV+Hhgwe4c+c+Hj16Iq67Cd29A9bWo2FTN3bED3ku7uHBsyo8e/7slffdvX0dxVlxcBnngH6KOliwdhsOnb+Mx/UX04jz/NlTlJecRUzQDpgYmEFLzw6btgehYP8RnDt3GgcL0jF3/FgYK+lg5SpPJKWkICbUH6baw6Ag/zNMhzthW0AU9h05igN707Fu8XSoDOqF/hoDMdLVBd6BESg6cBhHDhYhyMcTOgNVoadthaCYFFy+euOj7d1h7BAREclAttipP7crLyJ0t/frY+c1c/f2NRzIz8CSqZOhp6yDUU5uiEzJxdXbd18bFU+f3Mah4lQsc5sEfQMzTJ2zGoUHTuL+o+p9RY/v30TCbl8snDADXpv9kZCUgqig3TDWMMJ336piyUYf7D1xAQ+ePMO921cRG+wNK6Oh+GWQIiYvXIa8o6dw98kTVD29g9NHMuBgaghdVV1s9QvFyYtXUPXsdV/Zhx3GDhERkQwaK3ZuvXfsPMeta+UoyEjCxiULYaFlBGuz0fALjsXZy2V4UvW6j36ORw/LkZ64G2OtjWBpMwrb90ShtPzqS494hovHjiEzOhnZGcUoLixCTEgADNWNMETJHJGZhai4W734+dH9e8hMjMDEMTZQ0jTAsk3euFh5vSa0HqLiyn5MH20JIw0deHoH4OiZS3j6mj1OH3oYO0RERDL4KLHz/DluXb+K3JR4rHBzg42+GYZbOsJrRxDOX7qCR2885fw57t8vQWyYFyy0lGE/2glRyTm4fvPVr/nxw4e4c/0Wbt28gyuXziIpMggG6qbQ1BmJrCOncLfmzKqH9+8hJzUG05wdoGNsjU079uDazds1z/IA1yoOYfa44TAZqguP7f44cvoiY4eIiEhKPkbs3L15FWlxkZjl7AILPUvY207Etp0hOHupDFVvDQkhdi4jOsQTpuqDMcbBGXEZhfVi5+W5e/MKUmNCYaA5DNqGDsg5cQZ3hfVDYuzcRU5KDKZPcoSB+Qhs8QnE9Ru3aj7yAa6WH6yJHT3GDmOHiIik6PeMnWfPhDUyN5GZGA2XsWOhpWIMe3tX+AbHo+x6bWC8bZ6J1/iJD98KSx1VjHKYgKiU3HqxI+yxqSgvw+VLl3Hm5GEkhO+BsbY5dIwckXvyLO7W3HD05djRN7PFZsZO9TB2iIjoU/H7xc5z3LxRidyUGEwc7YDBivqY6LIUYbGZKK24/soj3zaPH1UgIykAY22MYW07GjuDYlFWeeOVxxzbXwCvDWuxYtVG+PruRrCvN4bpWTF23nUYO0RE9Kn4vWLnyaM7OH4gD8umuUBP3QB2Y2fCZ080Dh49jYrKSly/dg2VlZWorLyKiorbuHnrEZ48aTgqnj69i2MHsrFu8SwYGlpi8qxVKDhwCg8eV6/DeXLvOoK2bsQII1M4T5qNbd47Eey3A2b61oyddx3GDhERfSoaL3YuIMR3GyzM7WE5Zjryzlx4ETvCdXEqS08hcrcX9AYqos/PgzDWZRaWr92Abdu8sdPHBz4+PvD23o6dO30REZ2B/Ycu4vadR3U+S/U8f1aF6+WXkBkfCsdRYzHMwgGrNmxFdEIisrIzEBsejGkOY2GuY441a72QlJyEqGA/GA4dBk290fXW7GQnRWHqhFHQNraGh3fAq7FTdgAzxljCQE0LG7b64fCpC4wdIiIiKWms2Ll99RKiAn0xauQEjJ40/5V7Yz198ggnDhVg86oFGNSrJ7766huoa+vAwNAIxsZGMDKqpqenC9Nh5nBbtBpxKQW4euM1X4d4QeYHKC85jQCfrZjk6Ag7GyuMsLfBiDGjYGFlD3PTkZg7ZxUysgpx9vQxpMWHw8rUDqZWk1Bw+hzuvYide8hLj8ecaRNhbusA791huPFi/c9DXKs4jAWTRsPK0BRbdwbi2Fmeek5ERCQpjRU7D+5cx/6CHGzftgvefuE4W3ntpdh5jHOnjyIyZDdmz5wOBwcHODk5icaPH/+Co6MDnCdNwsYtO5BbdBA333gj0OfivbEunjmMyIAdWOI2Dc5OjnAYOx4O46dhyYotSM3ai8prN3D/znWcPLIfHhu8sGGzH85UVOJRzWGsJ48f4cyxQwgN9IWH1w5k5hXj3v0HNZ/jCe7cvoxwv23wXLse6dkFKK24xosKEhERSUljxc7zZ8/w+NFD3LlzF3fv3n/lDuHPnz/Hk8ePce/uHVy/fl1cm1NRUfFCee3b8nLx7c1bt/Dg4SPx7K23zbNnT/Hg3l1cr6hAydmLuHjyAq5cLhf3zjx6/FT83MJtKp48eYzbt+/g9p27eFJV9eLqzOLX9uQx7t27K77v4aNH1R9T/V7x+e/fvYM7t2/j4cNHqPqIdz5n7BAREcmgsWKH8+GHsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNERCQDxo50hrFDREQkA8aOdIaxQ0REJAPGjnSGsUNvlZ9ehoKMChRmCiobUIGCjHLkp5XV+1giok8VY0c6w9iht8pNKUF28iVkJl5EZuKFerKSLiI7+TJyU0vrfSwR0aeKsSOdYezQGxVkXEZ8SBG2bwjH2qW+WL5wB9wXesNdfLsd7gt9sG5lCHZuz0RSzGlxD0/d5yAi+hQxdqQzjB16rYKMKyjKPg/vdbswwsgWqoOGYkA/VQzop4aB/dQxoK8KBvbXhLbOSDhP2oAg/33Ym31VPOxV97mIiD41jB3pDGOHXis/oxRF2Sexet5yaA1Uw5BBWtDStYGR0UiYGtnDxHAEjA1HwcZqJmZO80FowEEUZ1ciP73+czVMiKIy8fHv8zHC2qD8en9e83xCaDG2iOh3wNiRzjB26LXy0y8jP+0w5k+ZC/V+mrC0cMac+d5YtzYUm9YEY8PqQKxfFYyNq2Owc0sOkqLOvNNhLOHfvDDrKopzqhVk3RAJ3w9FwmLnmlgRFkUXZV1FUVal+FYIqb05FeLHFGZfF/+senF0hfh8e7OuYV9GJfZlX8PemufiXiYi+lAYO9IZxg69XupFZMQUYuqYaVDubwCniSvh45uHhOjjSI4+Ka7RSY45heToM0iNPYfs5JL6z1GHsAcnJ/kCUqKPISaoCCF+WfDzyYW/bxEiQw4jOfYsspJLxMXOGfFnkRR1HEnC54o6jviwfYjck4mAXRnY7VuMqNCjSI0/i8zEc0iOOopIv3yEbEtH6M5cRNU8l7Bwuu7XQETUGBg70hnGDjWg+vBSdtI5xO1JxTjbSRgy2AyTZ3ggILgISVFHkBB5CsnxpchOuSIeNnr7HpSa96ecQ3RgFjYs2w5XRzeMNB8HGzNH2A53gfOkNVizJhqhQYeRFncOQd5JWL1kB9yX+MF9kTcWTl+BSaMmwcJ4NMzMXOHisgmeG6KwxzsBG5Ztw6SRrrA1GgVr0wmYOGEN1q2JQWTwETGc3v71ERG9H8aOdIaxQ/UIYSDIiD+FQK8w2FmMw4DBw2DrMBuLlmzB8oUeWODmhWXLwuCzPQvREceQIZx2/oZDWNWxcQnxodlYt2QD7M1HQW2gNgb/oga1gaoYIqwJUh4GK9s5WOoehtCg/di4bCtsze2hZ2gPY+NRMDccDl0VPfT5aTC+/0YR/QcYwdbKBbMnL8FE+ynQVzfA4D6D8MM3fdC7jz6sbedj/YZEpCddEg931f2aiIh+C8aOdIaxQ/XUxo5wqMlz+VaYm9rj597q6NlzAPr2+gU//vg9/v63f+I///4FhqbOWLQiBOHRp5AjXFjwNXtQCjOvICflGDa5b4S1iTXU1ExhaTsTy5YHYee2OKxZ7IHhZmMwZMgwDLOahQ1bkrF6qRd01DXxn56/YKCaCUaPXYylK4KwbvVuOI90QZ9vBuG7f/SD5mBrOI1dgdWrAuG10RdTxk6G8iAtDFA0wwQXD0TFnkWBcJZYA18XEZGsGDvSGcYO1VMdO+VICDuIBS4LoDJYCz/20oSKmjkszBxgO3wczAzMoNRnEPr0UoKpxWQsXRGG+OjTr10UXJhxGanRuZgyaiKU+w/FMHMXrFgfi/SMqziy7yHyko9i43IvWFtPgfnw+ViyKhruCzygozYUX/88AAbWU7F6cyqS0yuwr7AM/lv8odVfDd/8rSe01B3gvjwamenlOFhYjpAdERhl4YA+ffRgZb8QeyKOI4+nxBNRI2PsSGcYO1RP7Z6dxIgjWDFnHaxMxsDSehYWLg1GUNAhpMSdRlrkfngu3QxLPTOoKhnBxtYNO7xzUPiaqMhPOYeo3bGw0RsOpX6GmDrVE4FBB5GTWn3WVX7aWUSH5mDDhki4r4jCJs80LHFbBwN1A/RXNMFEVw8Ehx9DXlYl9uZeQqhvGMyG6kO5vxYcHZdi18786rOyMsoQE5CJqY5uUBxgCssR8+Efelj8uIa+LiIiWTF2pDOMHWpAdRRkJp1HVEABdm5JEq+QHBF6FBnJJcjPKENRxhXE7snGvCkLoK1uDvWho7FsdRSysirrXOem+n9nJ57EHq8QGKpZYPAAc8xdsBsxsWfFABFONc9PL0Fm0lnER59AdPgJRIYcwqoFG2E41AgqajaY7eaNuJjTKMq+in15lxDmFwErXWNoKRthypQN2BOwX9zwFGSUIT4oBzPGz8eQgcNgaVsdO7mMHSJqZIwd6Qxjh95IOJPpBeHPavb6FGVdQ2b8CXgs2w4jbVsMUrTE7EUBSM2ovuDfr+tjqgMjK+EE/DwDoatigcGK1liwNAjxiReQX+cGorV7ldLiTmPdok0w1jaBprY95s/bKZ7qLlxrpzZ2rHVNoKM2DK7TNiM48GC92FEaaAYrxg4RfSCMHekMY4deoxTZSeeRGH4YsaGHkRJ7puaaNdUxUpB5FdlJZ7BttS9Mde0xaKA5Zi7YjRThasgNxI6wZyfAKxgGapYYomiF+YsDEZdwXoyn6j07V5CVdAEpUceRGHEM0SEHsXr+Bphom0JLZxQWzN/F2CGiJoWxI51h7FAd1eGRl3YeccGZmOs8H+PsZsJ9aSDCAw8gN1V4gVegMPsaMhNOYtOyrTDUHoFBQ6zhtjQIqcIp3kK8vPR84tuUMwjfFQUzLSsM6WeCWXN8EBl1SnxsYXo5irJLEBeagzXzPeE2aTWWLPTD3KnLYKozDNqMHSJqghg70hnGDtXxa+xE+idijKk1fvmuP/QMnbF6TRwykstwIP8ODuReRYRvMqaMmoyhasOgbzwJaz2TkZN9tcHYKcy4hKSwbIy3GQ+VAXoYOWYRvLxzkJN9DYeK76Mw8xy2rfWGlf5waKtZw9llI2a7umOYrhljh4iaJMaOdIaxQ/VUr5spRVLkAayetxraqgboO8AYo8e4w2NjIkIDChHsk4T5kxdAX1kPhrr2mDZ9i3jl48LXREVRVhmyEk9g9fx1sDC0hp7BSExwWYdtO7MQFbYPOz1DMHGMKzTULGFsPhUr1kVj+cKNMNIyhoZWQ2t2wmGpbQgtZWNMneqBoFdiJxvTxs6FYn8TWNjMxW7GDhF9AIwd6QxjhxogREEZspLOIjIgEXNdF8BQywJDlY1hoGUFc7ORMDayg6a6BYz0HTDDdSN8d+QgPfHii5t41iWcwSVcQTnCLwlLZi3FcLOR0NG0FEPJ2mQETPUtMHSoNYZZTsfsuX4I8C/C+mVbYCrs2dEbg4ULfJEUc+ZF7ITvjsBwfVPoq5tj+vT6e3ZmTlgAZUVzWI9YwD07RPRBMHakM4wdeoMS5KacQPDOGCyYuhT2pqNhoDEMOlrDoKFlDZNhUzBz5jbs8s5CWvz514ZOterDYzlJJxG6Mw5LZq2Avbkj9NXMoKtmCD0dK9jYzsK8Bf7w8y1Gcsxp+HqGw3XifDg7r4TnxnikJZxHUVYFirMvIy4kA27O8zF57AKsWRWO6PDj1dfrSb+ClIj9WLt4BxxHLsCs2TsQHnUSucLFDut9TUREsmPsSGcYO/RaQjgUZJQiK/G0eIdy/60J2LI2DBuWh2Lj6ijs2JaBiODDSE+48OJ6OXWfo97zpQvPdwaxwUXw35aALetCsWZlKDasi8GuHdmIDjuG9MRLyE0pQUrUMYT55yMkoAgJkSeQk1Ly4hBbZsJpRATkI3R3PmLDjyEj6dKL6/sIZ5HFhR5EkG8+woMOivfGevXaP0REvx1jRzrD2KG3KEN+RoV4XZ29OddQnHUNBanXUJx5HftyrqMoSzh09D7/hkKsCM93FXtzrqI49ypyM28gP+um+P1QJByKqrnWjrCnRviz4uyr9W7kKXzfFInvuya+7+VDVML/FjZCe4X38/AVEX0gjB3pDGOH3k1NgNTz0gUB308Dz/XKWVzVav+8/se/+X0vnl/mr4+I6M0YO9KZZh87wg9EYc8EUXP0+lgkordh7EhnmnXsVIeOcEilUjysQtS8CIcMP97rj0jqGDvSmWYbO8LnzUy6gIjAYuz0SsbWjXHYujGeqFnYtikOvttSkBBxTLzvWd3XBxG9HWNHOtNsY6c4+zpiww5hlusqaGmaQmmwBlSVtaCqQvRpU1HWwmBFDegMNcemNaHiPc+EQ1p1XyNE9GaMHelMs42d/Xm3ELQrD8b6w9HjH63x4+D/A1WzzzHEmOjTpWzyOQYbfo6/f/cHtG3XBtMnr0ZW0kVxo133NUJEb8bYkc4029g5kHcL/t65MNCzRB/VVlgY1BLhF7vB/2gXok9W4Mku8DvUBcPd/oi2HT/HJEd3ZCUydohkwdiRzjT72DEysMZgvXbwyGyP/Od/QcqtHkSfrPT7PZB0XQET1nyODl2+hLPDcsYOkYwYO9IZxo6BNQZpt8OahHZIu/tnxFxRIPpkxVcqIOqyPBzdhdhpgUmOjB0iWTF2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAz8t6xk14mvkYLMipQkFmBQoHwvzPKkS+8r+7jiZoRxo50hrHD2KFm5H1jRwgaIXSE9xdmVaJIIPzvzF+Dp+7HEDUXjB3pDGOHsUPNyLvGTvXrsgTpsScQ7peFrWuDsHKBF5bM84L70gB4bkpA4J59SEm6hLzMCu7hoWaJsSOdYewwdqgZeffYKUNq9FH4bgrH/ClLYGtsB10VPagr60NTyxbmVq5wneWF7bvykJx8GQXcw0PNEGNHOsPYYexQM/IusSOETk7yOfh7RWPa6Fkw17aBsa4dRti4wHH0TIywcYKR/nCYmDjCeeoG+PoViYe0Cj7Sa5noY2HsSGcYO4wdakbeFjviouOMciRH7MWSGe7QHWIITWVLuEz1xK7dexEbdRR+XmGY4TQdhkOHQV3DFvMXBCBbiJ2Minqvs1dVL3YW1vsUZZUjX3h8RiUKMipR+PL6H3GdkPB8NQujxTVDZSjMKkO+sFboxXqhasLXXpReXu2lxdP1Pz9R42LsSGcYO4wdakbeFjtCKAgxEuQdh3EjnKCqbIrhI+Zgt18hCrJvoDjnOnKSTmP35lBMtJ+K3r10YTvaHbHJl5D9ltdy7WLnoswyFGVdRlbqFaSlVCI3XVjwLERPubj255VF0TWLoYuyLiI/8xyy0sqQk14bSDUhJDxnYgmKkkpRJHz9NcFT9/MTNTbGjnSGscPYoWbkXWJHELk7E8vcNsB10lqsWhGJtPjz2JdzHYXCnpj0K4jZkw23SUvR6ydtmFjPQXjCeWS+dm+KEC+lyEo8gRCfJKycswHOdi6wt3CCvd00ODuvxPLlYQjecxC5aWVIiTwCH89oeKyLxKY1Ydjg7oN5U+ZijJUjbK2nY/LkjdiwPhqRQfkI2hGHBVPdMd7aGaMsp2Di+JVYuTwcYYGHkZNSgsKM131NRL8dY0c6w9hh7FAz8rbYqT38kxl3ErF7ChHiU4iowCPISrosRpBw6nluyln4e0XAeZQrev+iC9sxyxAj7tlpOCzy00uRmXAUAdtDMct5NvRUDdD/hyEY2FMRiv2GYOBAHegaOsFl2lZEhJ1A2O4sTB0/E+bmjjAyGQNLE3sYaRig/08D8f3XA9CrlzYMDcZi5pTlmDNlEYZpm0GpzyD89O0v+OEHZWjrOWHuvADEx5xBUdbVel8PUWNh7EhnGDuMHWpG3hY7L6RcQnbCeWTEnUdmwiXkpgp7fYTDSaVIjMiF+5wVMDewhpKKBabN3oFUIXQaOHRUfUjqPEJ2xWD25NkwNbCGnv4oOE9agxXLfLF03no4jXaFvp49tPWdsHpTCnbvysDYEeOgqKSOvkq6MLOajFlum7F40XZMGTcHWkrG6P2tMjQGmcHBbi7mzN4M90WemDZxJgx1zKE4yBjDrGZjV8B+5OVcr/c1ETUWxo50hrHD2KFm5J1jpwHCIuHMhMPwWrsddpajoaFmAkvbWfDYkoacjApxYfOrHyOEThnyUo7DY/lmWOpbQUvDCuMmrYXfnv3ISr+ClOhD2LEpAM7j3KBvNBHz3KOw1SsRo23GoG//IeivZowJMzwREHIUqakXELQrFo4WY9Drq97o96M2JjitQ0DAfqQnnUaYbzxmOs+BqqIhhqjaY8P2bGTlXkduA38XosbA2JHOMHYYO9SMvF/sCGdPCUqRm3oR2UnH4ecVjLEjxkNpiCG09ByxYFkI4uLOVZ8ZVefjhT8T1vdkxO7FQpdF0BigBxMjZ6zdlIz01FLszb2JoswSpMQUw8sjDDNne2P1hgxsWheFUdaOUFTUha7JRKzZnILM7BvYl38NaXGFmDHOBcq/DIGW+ggsWRqKjORS7Mu7jvSYQ1i/eAv01K0xYJAlVokfd1XcK1X/70b02zF2pDOMHcYONSPvHzvCOp0S5CQfxq5NO2FrMhw//6QMdW1HzHDbhbCw4+Lp4HVDRyCcWp6fVoqEkGxMHTMTir/ow2b4PPgHHxKvulwoxlAp8tIuIjX+FKLCjiE++jx2bYnHWFsnqKuZw2bEXPj5FmJv3m3szSlHRnwh5kyaDu0hQ2Fl4QIPzzTx6yzOvoqM2KPYvHwnjLXsMXCgFVZ5JiEju5KxQx8MY0c6w9hh7FAz8u6xU1Zz08/LSIkuxLZ122BjZI4fvxuAIer2mO62C8FBR5AnXOem3uGrarWxExOQDmf7aRjQ2wgjRi1BcMQx5GdVvLjqcn56BYqzb+BQ4R0cLb6PCL8MONlPhNZQK4wcuQB7fAuwP+cmirPLkB5XADfn6dBR1oGtzXRs8cpETuoVceF0RswReLrvgLGWHQYNssYqz2TGDn1QjB3pDGOHsUPNyLvGTvXhq4tIjMjBeveNGD5sOH75RQVDDcdj6cpwhAQfRmZSiRgsr7uAX23sxAdlYcqYGRjUxxC29gsRGHZE3LNT/bHCY0uQmXAOKdEnkZFwEbu3JWCcnRO0tawxctQCBPgWYF/OjVdjR0kbw62nYfOWDMYOfTSMHekMY4exQ83Iu8WOsFfnMhIicrFmyXrYW4+GmpoJTG2mY8mqcISFHUVG8mXkC4e5Gnht1aq+wvEVpEQWYvaEeVDpZwArq5nw9i0UL0BYfff0K8hIOAq/zRFYPGMD1q4Ix9qVe+AwfCx0tK0xcvRCxg41WYwd6Qxjh7FDzcjbYqd6j045shOPY/uGXRhp4wA1NWPomThh/rIgBIceRnzUCSRHnxL3xCTHnEJq/DlkpJYgN1VYf/Py66z6bKyshMNYMWcNDFRNYWwwDouXhyE+/jyKcoXTwi8iIiAZc10WwkjTGs6TN2LZst0YbV0dO6MYO9SEMXakM4wdxg41I2+LHSFOhIsHRgdkYIbTLCgP1oeiqjkcnFdg7fpIeG9JxHbPOGzziMHWTTHY7pkA/4AixCZeQGa92Kl+vvy08/DZtAcO1mOhq2WFEWMWwmtnDpKTziM2JB/rlm6GzbDRGDjQCK5zd8FzSywcbcdDRziMJcSOH2OHmibGjnSGscPYoWbkbbFTmFmKwsyz8HD3hOYAVfxZ/p/o8bdv0XfgUKipGkJZURtKitoYoqiFIYP0oKluC5cZWxEcfQrpKSX1XmfVFxW8gqTwImxy98Qom9FQUdKFhro1zI3sYW5gDk01Q6iq28DCdj68fYuxxy8NY6zHQFXFFDYj3OC/K/+l2MnDjPGTodZPBebDJmGTZ+qvsRN9GBuXbIWOigV6/WIC900JjB36oBg70hnGDmOHmpG3x85lFGQew4alG2Coqo9eP/TF11/9iP/86zv8+4Vv8dU/v8W///UzfvpBE2MnrEVY1Elk1MTOq+t4ysS7mBemX0JKRD42LduE4YZW+OmfP+PfCv/At199i779dWBjvxDrN6YiI7kMMYG5mD15AUYMn4qpUzciNGA/9mZfR1FWGTLi92H5nBWwN3WA8/jl2LEjV4wd4cyxzLjj2LEhGGOGT4exsQs8tmchM6uCsUMfDGNHOsPYYexQM/K22BEuICichRUfthd+XgnYtjEKm9eFw3NtGDzqCceW9XEI8i9GetIl5DTwOqslLFTOTj6HhPD92OOdjC1r9mD1st1YtTwUnhvjxXU5CdFnxBuBZiacReSeAuzZlYOwPfuQHn/+xWLnnJTziAkuQuCODITsLkJS7Nma5y9DbspFJEUeRfCuXOzekYOE2DPIfc2ZYkSNgbEjnWHsMHaoGXlb7Pw+qi8kmJ50GWmJQgTVfT+RNDB2pDOMHcYONSPvGjvirR4yKqovLPgWBe/8Gq4+00tYAF2YWV59HZ70CvHzCH/26/V6fn1cQ8/94n2vfEzt+6oXWDf0PqLGxtiRzjB2GDvUjLxr7BDR2zF2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY4exQ80IY4eo8TB2pDOMHcYONSOMHaLGw9iRzjB2GDvUjDB2iBoPY0c6w9hh7FAzwtghajyMHekMY8fAGoo67bAuqR0yHvwZcRUKRJ+sxOtC9Mhj7Aohdr5k7BD9Bowd6Uyzjp2AmtgZqNUOq+PaIvV2D0SXKBB9suLKFRB5UR6Oy75Ahy4tMWksY4dIVowd6Uyzjp09PjnQ07HAP779E/TH/gET134Ox2VEn65xyz+Hw5LPMcDgD+jYuR1cnVcjK4mxQyQLxo50ptnGzv68Gwj1L4K1xXj06NED7Tu1QVc5QVuiT1gbdJNrh27dO+OH7/tg+eKdyEq6hMLMinqvESJ6M8aOdKbZxo6wcU+JPY2tm6IxZ8YGTHFagSnjV2CK00qiT9gKuDitxIwpa7F8kQ/C9xQhJ6UE+ell9V4jRPRmjB3pTLONHUFuaimyky8hM/ECMhLOIyNBeEv0qTuPjMQL4uErIXTqvi6I6N0wdqQzzTp28tLKUJBRIX7DFmURNSOZleLeTe7RIZIdY0c608xjh4iISDaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6Qxjh4iISAaMHekMY4eIiEgGjB3pDGOHiIhIBowd6YxMsfP8+XPcv3cHV0ou4dDBQzhx8gxu3L6Lp1VVdR/6yjB2iIjoUyF77DzH0yePcONaJY4fO4qiomIUFha+pBhFxQdw8MgJXLhchlv3HuBp3afgvNfIFDuPHz7AsQMF2LphBcxMjeDoPA0JmUWovH4bz+s++KV5OXa2borB3pwbKMioFIOHiIhISoqyriE37Qo2b4h8r9h5VvUUtypLkB4XglF2Nhg0SBGKiooYMmQIhgxRwpAhalBRN4KplRPmL9+M+Nx9KLv/4I0/XzlvHpli587NEsSF+WCKozVUVPpCSdcA89Z44fDZi3hS98EvjRA7EyY44Zuvf8aOLYk4XHQP+/NuYV/uDSIiIkk5WHAHxTnXsM0zTowdO7vh7xg7T3Ct9DSCfTahT8+++Orrn6CtbwhLa2tYWVrB0twCFuYW0NPRh57+MLi4LUZYSqZ4BIUj28gQO09Rcn4/tqxZjNHWppgw2R6GluawtJ+ExNy9uPno9blTUlICZ2dn/O0v/8KUCUvgtSEanmsj4LEmjIiISFI2r4/CxtWh4s+zf/zt33BwGPPusXPlDIJ3eKJ/bzXoGo/ENv9AJGdkID0tDWnJiUiOC4PHqvmwMzeCvr4ppsxehkOnztV9Ks47znvHzrOnd7A/LwlzXV1hY2GFtR7LMG7cGGipm8AnMBrnyq+i6nnDO9vKy8uxcOFC/Purr9G/rzK0NIwxVKBOREQkPZpqRhg8SAPff/cjFi1aiHv37tX90Vdvfo2dzRjQWxPWY6Yjde8BlN+6hVuCmzdw83o5juzNxAb3eTA1MoOx1TjE5+3Fs7pPxnmnee/YuXm1BBGBPhjv4AS7UU6ISAjEqmVu0FEeisUrNyJ3/xE8ePS47oeJIxRvTEwMpkyZgpEjR8Le3l58S0REJDW1P8McHR0xY8YMJCYm4vHjhn/+vTy1sRO0YzP699bEiPFzkHfyDB7Wedy9mxWIDfHDKPsx0B02GiGZ+RCeveHdCZw3zXvHzulj+7Fm6TyMHOmA6fOX4MDxAsSFbcUIU0M4TnCFf1gcrt68XffDxHn27JlYvZWVlSgtLUFJyWUiIiJJu3KlFFevXsWDBw/Es5XfNnVjx9ZxNnKOHMedx4/x9OlTPH36BFVVT1F++SzCfLdjvOMEDB83DQl7D0M45/ntn4FTd94zdh4jJyUEk0bawNFhArx2BeFKZRnOHMrCPNeJ0DexxbxVm3Hs8hX+Y3A4HA6H08C8OIzlswUDeg+FhY0zouKTcfjoURw9egRHDu/HwX1ZCNy2HlPtR8FxpBOWb/TByZKyuk/Fecd599h5/gyPH5QjwHsNLAyMMW32IqQXHcGjqud4cq8MAd7rYaBjDIeJs5CQvw/3n/CqABwOh8Ph1J3a2AnZuQX9f1ZBv94amDB+ItzcZmPWrBmYMX0ypjhZwUCtPwb+3B8jR7sgMDodt+89qPtUnHecd46dqiePcOFEIZbOnQk9QyvMXbkJhSdO4/b9e3hwvxyJUTthb2IIGyt7ePoE4mLF9bpPweFwOBxOs5/q2DmL0J1b0PcHRfzz7z9CTX0ojEyMYWxsCCNDHehqDMCgfj9iwCAV2I6Zim2+Ubhcdg3PnvMwlizzzrHz4O51JEXswrjRdtA3G4Hpi1YgOCYWGZkZyM5OhZ/3eoy1MYWpkRGmzF6M3EMn+A/C4XA4HE6dqY2dkJ2b0fcnZQwcYoBZi5bCc/s2eHtvh/d2L2zbsh6rls+H8wQnDLceg0mT5iEuJQ837j3Es3dYF8R5dd4xdp7gWsVpbFgyA4bamjCxsoXTlGlYuHgx3Jctg/vy5VgwdyYc7cygPXQojCxGwz8mDcIJePwn4XA4HA7n13llgfIvGrAcNQ3JxQdQcfuWeNby3Tt3cOfObVy5fBqRQTvgZGcHPXUjLF61FccuXEHVM56A/r7zTrFT9fQ2zp3IxSRrCwz+qTcsrWzgOG48JkyYACcnJzg5TYTzRCeMsreGyhBVDBygg2UbduLCjdv8R+FwOBwO56WpezaW/YR5KD57UTzT6tV5jgun87Fyvgv0VdXhMGEmUvIPvPU+lJz689bYEU6ju3X1MjLiAqCvMhQqSrpYudETQRERiIyMRER4OMLDIxEbGwF//y1wdhwJtYEqGDN+BlILD+Dx49dfUZnD4XA4nOY2dWNHuM5O/smzeFT3gcL16W6dwvb182CmpYFRjlORmL0XT57yBKD3nbfGTlXVQ5w6UohNy+dBSUkLds5zkH/8FO5WVYnHDZ9VVaGqSjhYVYXbty4gxG8T7MyMMFTHFGu2BeD63Xs8lMXhcDgcTs28GjtDYTvWDTlHT+LOkycvrrPz9MkD3L9biYP74jHXdSy0VTUwbd5K7D1xHk+f8ojJ+85bYucZHtwvQ0ZCAMaPMIOW7jC4b/TB+SvlDQbMk8d3kZ8Zj3muzhg4UA32znNw6GIJHjzjLjcOh8PhcIT5NXY80a+XGvTNHLArIhq5xcUoKipCUVEhigvTkRzvh5XLpmGYiRG0DazhuTsCpTfv4JlwShbnveYtsfMEV8tOwH/bWhioaMB2lDPCErNw7TVXSH7+rArnTx2G75a10BysDG09K0Rm5KP81h2uHudwOBwO55WzsTzR/5dB+Kn3YNiOGYsp01wxdapgGqbPcMHkyY4YYWcLm5HjMXPxBmQfOI4Hz57heYO7GzhvmjfGzrNnj3Dl4jH4b90MO7ORcF+zDYfOXMT9hw0dWRTmOe7eKEdhRiymOY6CvfVIBEUn41LZVVSxRDkcDofDwfNnT3Gr8jJSogNhbWGOgYMGQ11zKLR1dKCtrQsdHQMYmpjBwnYkxk1xw5ot/kjNO4zrt+8zc2ScN8aO8A9y9/Z1nDx6FOnJWTh64izuPHj0xjOsnj19hJtXr2B/fjYyU9Jw6swF3L57n3t2OBwOh8MR5vlzPHl4D1cunUN6egpCQ0MQFBSEoMBABAYGIygoBKFhUYhJSEF2wX6cPn8Ft++9/QajnNfPG2OHw+FwOBwOR+rD2OFwOBwOh/NJD2OHw+FwOBzOJz2MHQ6Hw+FwOJ/0MHY4HA6Hw+F80sPY4XA4HA6H80kPY4fD4XA4HM4nPf8fo09qWaQPUZIAAAAASUVORK5CYII=[/img] [br][b][u]SORU 5: [/u][/b]Yukarıda verilen ABCD karesinin içerisine, üst tarafta[br]bir paralel kenar ve alt tarafta ise bir dikdörtgen çizilmiştir. [b]Buna göre[br]mor boyalı bölgenin alanı kaç cm[sup]2[/sup] dir?[/b][br][br][br]
[b][u]SORU 6:[/u][/b] Kenar uzunlukları metre cinsinden bir doğal sayı ve[br]alanı 48 m[sup]2[/sup] olan dikdörtgen şeklindeki parkın çevresi tel ile[br]çevrilecektir. [b]Buna göre [u]en az[/u] miktarda tel kullanılması için bu parkın[br]çevresinin kaç metre olması gerekir?[/b]