Calculus - Applications of Integrals - Areas and Volumes

Ms. Orr, Apr 9, 2020

This book will help give some visualizations and activities to guide you through the process of understanding applications of areas and volumes.

Table of Contents

  1. Areas
    1. Finding the Area Between Two Curves
    2. Areas Between Curves
    3. Areas Between Curves dy Rectangles
  2. Discs
    1. Volumes - Discs (Perpendicular to the x-axis)
  3. Washers
    1. Visualization of a Single Washer
    2. Washer Method
    3. Volumes of Solids - Disk & Washer Method
    4. Region between two quadratics rotated about y = -3
    5. Volume of revolution--washers
    6. AB2007_1b_Modified Volume by washer
  4. Perpendicular Cross-Sections
    1. Solids Formed From Certain Cross Sections
    2. Visualizing volumes by known cross section
  5. Culminating Activities
    1. Areas & Volumes: Culminating Activity
  6. BC - Shells
    1. Cylindrical Shell Action!!! (1)
    2. Cylindrical Shells: REVAMPED!
    3. Volume by Cylindrical Shells: Illustrated

1.

Areas

  • 1. Finding the Area Between Two Curves
  • 2. Areas Between Curves
  • 3. Areas Between Curves dy Rectangles

1.1.

Finding the Area Between Two Curves

Move the sliders or change the functions to approximate the area between two curves.
Finding the Area Between Two Curves
– Chris Mizell

1.2.

–

1.3.

–

2.

Discs

  • 1. Volumes - Discs (Perpendicular to the x-axis)

2.1.

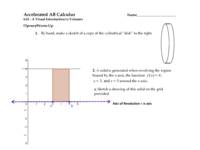
Volumes - Discs (Perpendicular to the x-axis)

Instructions
Use the following Geogebra Visualizations to help you as you work through the beginning stages of developing the concept of Volumes of Revolutions - "Discs Perpendicular to the X-Axis."[br][br]More resources to come!!
6.01 Volumes of Revolution - Disks
– Michael Borcherds, Ms. Orr, Tim Brzezinski

3.

Washers

  • 1. Visualization of a Single Washer
  • 2. Washer Method
  • 3. Volumes of Solids - Disk & Washer Method
  • 4. Region between two quadratics rotated about y = -3
  • 5. Volume of revolution--washers
  • 6. AB2007_1b_Modified Volume by washer

3.1.

Visualization of a Single Washer

Instructions
Play around with the visualizations and they uses them to help you develop a basic understanding as you begin to work on "6.02 Volumes of Revolution - Washers" Use the other GeoGebra Activities in this chapter to help guide your geometric understanding of the calculus.
A "BEHIND-THE-SCENES" view: Here, f and g (graphs not displayed) are constant functions.
6.02 Volumes of revolution - Washers
Quick (Silent) Demo
– Ms. Orr, Tim Brzezinski

3.2.

–

3.3.

–

3.4.

–

3.5.

–

3.6.

–

4.

Perpendicular Cross-Sections

  • 1. Solids Formed From Certain Cross Sections
  • 2. Visualizing volumes by known cross section

4.1.

Solids Formed From Certain Cross Sections

[b]This applet illustrates solids formed by "prism stacking". [/b] [br][br]Various possible cross-sections are shown to the left. Select any one you'd like. [br][br]f = greater (upper) function[br]g = lesser (lower) function[br]n = number of equal intervals into which the interval [a, b] is divided. [br][br]Note: Cross sections are drawn parallel to the y-axis. [br][br]Enjoy!
Quick Demo. (BGM: Andy Hunter)
– Tim Brzezinski

4.2.

–

5.

Culminating Activities

  • 1. Areas & Volumes: Culminating Activity

5.1.

Areas & Volumes: Culminating Activity

[b][color=#0000ff]For each exercise, write a definite integral, with respect to the indicated variable, that expresses the area or volume being described.  Then, evaluate that definite integral using the fundamental theorem of calculus. [br][br][/color][color=#ff0000]Note: The values of each pair of definite integrals (displayed in the same color) should be equal![/color][br][/b][br][color=#980000]1) Area of R1 (Integrate with respect to x).  [br]2) Area of R1 (Integrate with respect to y).[br][/color][br][color=#45818e]3) Area of R2 (Integrate with respect to x).[br]4) Area of R2 (Integrate with respect to y).[br][/color][br][color=#ff00ff]5) Area of R3 (Integrate with respect to x).[br]6) Area of R3 (Integrate with respect to y).[/color][br][br][color=#0000ff]7) Volume of solid of revolution formed by rotating R1 about the x-axis[br]    (Integrate with respect to x.)  [br]8) Volume of solid of revolution formed by rotating R1 about the x-axis[br]    (Integrate with respect to y.)  [/color][br][br][color=#9900ff]9) Volume of solid of revolution formed by rotating R1 about the y-axis[br]    (Integrate with respect to x.)  [br]10) Volume of solid of revolution formed by rotating R1 about the y-axis[br]    (Integrate with respect to y.)  [/color][br][br][color=#b6d7a8]11) Volume of solid of revolution formed by rotating R2 about the x-axis[br]    (Integrate with respect to x.)  [br]12) Volume of solid of revolution formed by rotating R2 about the x-axis[br]    (Integrate with respect to y.)  [/color][br][br][color=#ff7700]13) Volume of solid of revolution formed by rotating R2 about the y-axis[br]    (Integrate with respect to x.)  [br]14) Volume of solid of revolution formed by rotating R2 about the y-axis[br]    (Integrate with respect to y.)  [/color][br][br][color=#ff0000]15) Volume of solid of revolution formed by rotating R3 about the x-axis[br]    (Integrate with respect to x.)  [br]16) Volume of solid of revolution formed by rotating R3 about the x-axis[br]    (Integrate with respect to y.)  [/color][br][br][color=#000000]17) Volume of solid of revolution formed by rotating R3 about the y-axis[br]    (Integrate with respect to x.)  [br]18) Volume of solid of revolution formed by rotating R3 about the y-axis[br]    (Integrate with respect to y.)  [/color]
– Tim Brzezinski

6.

BC - Shells

  • 1. Cylindrical Shell Action!!! (1)
  • 2. Cylindrical Shells: REVAMPED!
  • 3. Volume by Cylindrical Shells: Illustrated

6.1.

Cylindrical Shell Action!!! (1)

ONE SHELL:
[b]For another detailed illustration, go to [url=https://www.geogebra.org/m/SWBXZQxR]Cylindrical Shell Action!!! (2)[/url][/b]
– Tim Brzezinski

6.2.

–

6.3.

–

Information