IM Geo.3.13 Lesson: Using the Pythagorean Theorem and Similarity
[size=150]Is triangle [math]ADC[/math] similar to triangle [math]CDB[/math] in the applet below? Explain or show your reasoning.[/size]
The two smaller triangles are copies of the ones that make up the biggest triangle. Convince yourself all 3 triangles are similar.
Write 3 similarity statements.[br]
Determine the scale factor for each pair of triangles.
Determine the lengths of sides [math]HG[/math], [math]GF[/math], and [math]HF[/math].
Convince yourself there are 3 similar triangles. Write a similarity statement for the 3 triangles.[br]
Write as many equations about proportional side lengths as you can.[br]
What do you notice about these equations?[br]
In the applet below, Tyler says that since triangle [math]ACD[/math] is similar to triangle [math]ABC[/math], the length of [math]CB[/math] is 11.96. Noah says that since [math]ABC[/math] is a right triangle, we can use the Pythagorean Theorem. So the length of [math]CB[/math] is 12 exactly. Do you agree with either of them? Explain or show your reasoning.
IM Geo.3.13 Practice: Using the Pythagorean Theorem and Similarity
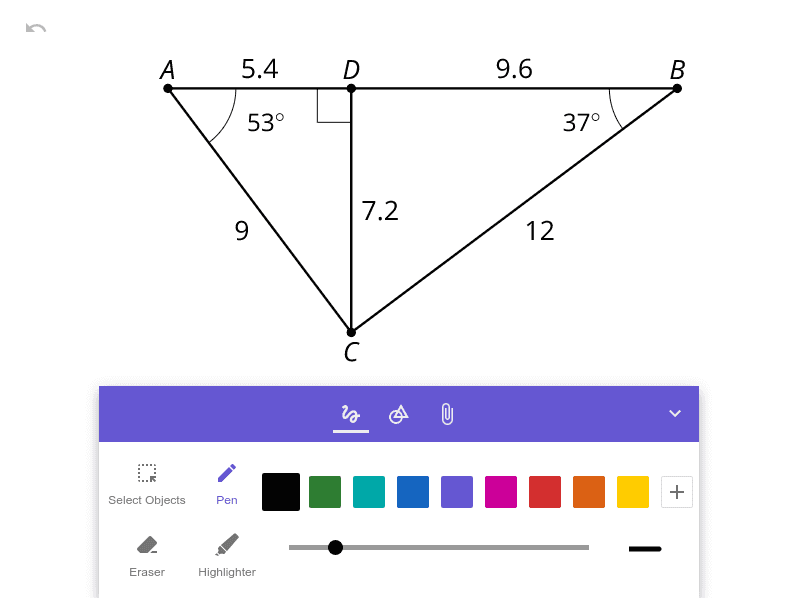
In right triangle ABC, altitude CD is drawn to its hypotenuse.
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUYAAACkCAYAAADrLIfNAAASJElEQVR4Ae2dSYwU1R+A52bUgyQaLh4gKu7KqIC74II6iIILuDMY9eAB4YYeDKiJGDVBo4ACMwPMAio4gMAwbIP7ciEhaji4J3IyIXpTE98/v/f3zVR3V3dXd7+qeu/VV0mnqmt5y/er+vpXVV3dbYoBAhCAAARKCLSVvOMNBCAAAQgoxMhOAAEIQKCMAGIsA8JbCEAAAoiRfQACEIBAGQHEWAaEtxCAAAQQY0r7wE8//aSWLFmi2tvbVVtbmxo3bpyaO3eukvkMEICA2wQQYwrxOXLkiBbh9OnT1eDgoBoZGdHjxYsXp1AbRUIAArYJIEbLRCUjlOyws7PTcskUBwEIZEUAMVomLUKcMGGC5VIpDgIQyJIAYrRI+8SJE/p6Yk9Pj8VSKQoCEMiaAGK0SFyEKDdaRJAMEICAvwQQo8XYLVu2TIvRYpEUBQEI5EAAMVqELmKcOHGixRIpCgIQyIMAYrRIfeXKlZxKW+RJURDIiwBitEhevqoj1xglc2SAAAT8JYAYLcfOXGeUp1yWL1+uXzItX/pmgAAE/CCAGFOIkzzpIk+5yJMv8hJZcqc6BdAUCYGUCCDGlMBSLAQg4C8BxOhv7Gg5BCCQEgHE2ADYH374QW3dulUdO3asga1YFQIQ8I0AYkwYsRUrVug7znLXWV7PPvtswi1ZDQIQ8I0AYkwQsd9++61EikaOR48eTbA1q0AAAr4RQIwJIjY0NBQrxt7e3gRbswoEIOAbAcSYIGLHjx+PFeOZZ56p+CWdBABZBQKeEUCMCQP29NNPl8hx0aJFauHChXqePB+NIBOCZDUIeEAAMSYM0pNPPqnGjx+vRTgwMDC6lTwGiCBHcTABgSAIIMYEYfz666+1EJcuXarHhw8frtgKQVYgYQYEvCWAGBOE7oknntB/V/DNN99UFaMpRgTZ0dGh1+MU21BhDAG/CCDGOvH66quvtORef/11lUSMUtzzzz+vPv74Y06x67BlMQRcJYAY60Tm8ccfH/3x2SRi/Oijj1RXV9doqZxij6JgAgLeEECMNUL15Zdf6mzxjTfe0GslEaNkiz/++GNFqQiyAgkzIOAsAcRYIzRytzn6VwX1xCjZYnd3d40SlUKQNfGwEAJOEECMVcLwxRdf6Gxx5syZanh4WP399991rzFWyxbjqkCQcVSYBwE3CCDGKnF47LHH1FlnnaXkqRf53qL8aMTatWu1LOO+rpMkW4yrCkHGUWEeBPIlgBhj+Jts8c033xxdKoJ85ZVXtBhfffVVnUGOLvzvTnTctcXoOrWmEWQtOiyDQLYEEGMMb7m2ePbZZ1csMdcYn3vuOfXMM8/oU+y//vpLNZstVlSguAYZx4R5EMiaAGIsI/7555/rrPCtt94qW6JKrjGaU2wR5KOPPhp7J7qigAZmkEE2AItVIWCZAGIsA9rZ2anOOeecsrn/f2syxug1RhHkd999F7u+jZkI0gZFyoBAYwQQY4TXZ599prPFVatWReaOTcaJcWxpulMIMl2+lA6BKAHEGKGxYMECNWnSpMic0sk8xWhagiANCcYQSI8AYvyP7aeffqqzxdWrV1el7YIYTeMQpCHBGAL2CSDG/5jWyxZlNZfEaHYFBGlIMIaAPQKIUSn1ySef6GxxzZo1Ncm6KEbTYARpSDCGQOsEEKNS+us25557bl2aLovRNB5BGhKMIdA8gcKLUX43Uf4O9e23365L0Qcxmk4gSEOCMQQaJ1B4MT7yyCMqSbYoaH0So9kVEKQhwRgCyQkUWozyKJ9ki++8804iYj6K0XQMQRoSjCFQn0Chxfjwww+r8847rz6l/9bwWYymkwjSkGAMgeoECitGeaxPskX5KbGkQwhiNH1FkIYEYwhUEiisGB966KGGskVBF5IYza6AIA0JxhAYI1BIMY6MjOhscd26dWMkEkyFKEbTbQRpSDCGgFKFFOODDz6ozj///IbjH7IYDQwEaUgwLjKBwonRZIvr169vOO5FEKOBgiANCcZFJFA4MT7wwANNZYuycxRJjOZgQJCGBOMiESiUGA8dOqSvLXZ1dTUV4yKK0YBCkIYE4yIQKJQY77//fnXBBRc0Hdcii9FAQ5CGBOOQCRRGjAcPHtTZYnd3d9PxRIxj6BDkGAumwiNQGDHOnz9fXXjhhS1FEDFW4kOQlUyY4z+BQojxwIEDOlvs6elpKWKIsTo+BFmdDUv8I1AIMdrIFiW0iLH+Do4g6zNiDfcJBC/G/fv362xxw4YNLUcDMSZHiCCTs2JN9wgEL8Z58+apiy66yAp5xNg4RgTZODO2yJ9A0GLct2+fzhY3btxohTRibB4jgmyeHVtmTyBoMd53333WskUJDWJsfQdFkK0zpIT0CQQrxuHhYZ0tbtq0yRpFxGgNpUKQ9lhSkn0CwYrx3nvvVRdffLFVYojRKk5dGIK0z5QSWycQpBj37t2rs8Xe3t7WCUVKQIwRGJYnEaRloBTXEoEgxXjPPfdYzxaFMmJsaV9LtDGCTISJlVImEJwYTbbY19dnHR1itI60aoEIsioaFmRAIDgx3n333eqSSy5JBR1iTAVrzUIRZE08LEyJQFBiHBoa0tcW+/v7U8GFGFPBmqhQBJkIEytZIhCUGOfOnZtatii8EaOlva6FYhBkC/DYNDGBYMS4Z88enS0ODAwk7nyjKyLGRomltz6CTI8tJQf0L4Fz5sxRl156aaoxRYyp4m2qcATZFDY2qkMgiIxx9+7dOlvcvHlzne62thgxtsYvza0RZJp0i1d2EGLMIluUXQMxun+AIEj3Y+RDC70X465du3S2uGXLltR5I8bUEVurAEFaQ1nIgrwX41133aUmT56cSfAQYyaYrVaCIK3iLExhXovxww8/1Nniu+++m0nAEGMmmFOpBEGmgjXYQr0W45133qna29szCw5izAx1ahUhyNTQBlWwt2LcuXOnzhbfe++9zAKCGDNDnXpFCDJ1xF5X4K0YZ8+enWm2KFFGjF7v67GNR5CxWAo/00sx7tixQ2eL77//fqYBRIyZ4s60MgSZKW7nK/NSjHfccYe67LLLMoeLGDNHnnmFCDJz5E5W6J0YTba4devWzIEixsyR51YhgswNvRMVeyfGWbNm5ZItSrQQoxP7bKaNQJCZ4namMq/EuH37dn1tcdu2bbkARIy5YHeiUgTpRBgya4RXYuzo6FCXX355ZnDKK0KM5USK9x5BFiPm3ohxcHBQZ4sffPBBbpFBjLmhd65iBOlcSKw2yBsx3n777blmi0IdMVrd94IoDEEGEcaKTnghRskS29ralGSNeQ6IMU/6bteNIN2OT6Ot80KMt912m7riiisa7Zv19RGjdaTBFYggwwip82KUO9CSLcod6bwHxJh3BPypH0H6E6u4ljovRleyRYGHGON2IebVIoAga9Fxd5nTYpSnWyRblKddXBgQowtR8LMNCNKvuDktxltvvVVNmTLFGaKI0ZlQeNsQBOlH6JwVo/xyjmSL8ruLrgyI0ZVI+N8OBOl2DJ0V48yZM9XUqVOdoocYnQpHEI1BkG6G0Ukxyq9yS7Yo/+ni0oAYXYpGWG1BkG7F00kx3nLLLc5lixI2xOjWzhtiaxCkG1F1TowmW5T/i3ZtQIyuRSTc9iDIfGPrnBhvvvlmNW3atHypVKkdMVYBw+zUCCDI1NDWLNgpMcr/Q8u1xd27d9dsdF4LEWNe5KkXQWa7DzglxptuusnZbFHCghiz3TmprZIAgqxkksYcZ8S4ZcsWnS3u2bMnjX5aKRMxWsFIIRYIIEgLEGsU4YwYb7zxRnXllVfWaGr+ixBj/jGgBaUEEGQpD1vvnBDj5s2bdbY4NDRkq1+plIMYU8FKoRYIIEgLECNFOCHGGTNmOJ8tCjPEGNlzmHSSAIK0E5bcxTgwMOBFtii4EaOdnY5S0ieAIFtjnLsYJVu86qqrWutFRlsjxoxAU401AgiyOZS5irG/v19ni3v37m2u9RlvhRgzBk511gggyMZQ5irG6dOne5MtClbE2NjOxdruEUCQyWKSmxj7+vq8yhYFJ2JMtlOxlvsEEGTtGOUmxhtuuEFdffXVtVvn2FLE6FhAaE7LBBBkPMJcxNjb26uzxeHh4fhWOToXMToaGJrVMgEEWYowFzFef/316pprriltiQfvEKMHQaKJLRFAkP/Hl7kYfc0WBRdibOmYY2OPCBRdkJmL8brrrvMyW0SMHh3VNNUagaIKMlMxbtq0SV9b3Ldvn7XAZVkQGWOWtKnLJQJFE2SmYrz22muVvHwdEKOvkaPdtggURZCZiXHjxo06W9y/f7+tGGVeDmLMHDkVOkogdEFmJka5C+1ztij7J2J09CilWbkRCFWQmYhxw4YN3meLiDG3Y4+KPSAQmiAzEaM84SJ3o30fyBh9jyDtT5tAKIJMXYw9PT06Wzxw4EDaMUm9fMSYOmIqCISA74JMXYyhZIuyvyLGQI5aupEZAV8FmaoYu7u7g8kWEWNmxxIVBUjAN0GmKkb5ZW55LjqUgYwxlEjSj7wI+CLI1MTY1dWls8WDBw/mFQPr9RoxrlixQu3atavqa+fOner777+3Xj8FQiAUAq4LMjUxyn9Eh5Qtyg5pxPjaa68peayx2ksuIbz44ouh7MP0AwKpEXBVkKmIcf369cFli7JnGDEePny45o5y7NgxtXr16prrsBACEBgj4JogUxHjtGnTlPxCd2gDYgwtovTHNQKuCNK6GE22eOjQIdeYt9wexNgyQgqAQCICeQvSuhinTp0aZLYo0USMifZpVoKANQJ5CdKqGNetW6evLYaYLUqkEaO1/Z2CINAQgawFaUWM//zzj/r222/VlClTlPxXdKiDEePIyEjNLnLzpSYeFkKgaQL1BHn8+HH1yy+/NF2+2bBlMa5cuVKdcsopOlNsa2tTL7zwgik7qHF/f786/fTTdT9PPfVUtWbNmqr9Q4xV0bAAAlYIxAly/vz5ox7q6OhQf/zxR9N1tSRGk0GJEM3rjDPOUP/++2/TDXJxwz///FOdfPLJo300ff35559jm4sYY7EwEwLWCUQFaY5LM37qqaearq8lMa5du7ZCFqZRjMc+LGABC/aB7PeBSZMm5SNG+SmxuIBv27ZNyXW4UF59fX2x/ZQvcYfSR/oRzv5axFjOmjWr4hidPXt2PmKUWufNm1fSoKVLlzbdGJc3XLRoUUk/FyxY4HJzaRsECkXg6NGjavz48aPH6EknnaSTlmYhtHQqbSrdsWOHevnll1tqiCnL5bH8kddLL72kfzzC5XbSNggUkcDvv/+u5PLeqlWr1K+//toSAitibKkFbAwBCEDAMQKI0bGA0BwIQCB/AnXFeOLECbV8+fLgT5PrhWLx4sVqxowZoy9hIl8VYIAABPwiIMetHL/Rl9ywig51xbhs2TJ9QVPEUORB7r53dnYq4SGvCRMmqHHjxqkjR44UGQt9h4B3BMwf9JljWZ7Wk+N74cKFo32pKUbJFuXglw1DftRvlEaVCZGfgItKUNgIk4kTJ1bZitkQgICLBCTJK/eZPMEnx7gZxqbMnMjYFCAbtbe3R5YUa1L6f9ppp1V0enBwsEKYFSsxAwIQcIrA5MmT9VlftFHmWJaER4aqYpTzcDGo+bJo1KbRAoswLafQ5Z8w0m+BaBgVgQN9hEAIBOSYFRGaQY5juX8QPcarijEqA5GjFFbUmw1xnzACNfrhYSAzhgAE3CVgXCZnwOZmqtwvkLNjky1K62PFaDaOXlMrcmZU/gljwh7HySxjDAEIuEdALouJCM2NFxGiXCZbsmRJSWNjxSgppcig/CV3c4o2GPlFP00MA4EqkBkgAAE/CMiZ8Jw5c0oaG3dztUKMRgRyDi7T5lXtdLKkhgDfmK/mlHfNwJTlDBCAgB8ETLZY3lpJAqOJX4UYZUOxavkgWWTc/PL1Qnsvny5xnzDyNSb5sGCAAAT8IFDtZqn5XmPJpcNol2QFOd+udtoYvWsT3S7kafmgkIu05lvyMi2fLvIhEccpZBb0DQI+EzBnw9u3b1fy3/AylmuLkuTIZbHoUJIxSmYkFyfjBpFm0TJGEZ98GJiX9F9OnYt6dz5uv2AeBHwhIA4zx7IZi/NEmOVDiRjLF/IeAhCAQBEJIMYiRp0+QwACNQkgxpp4WAgBCBSRAGIsYtTpMwQgUJMAYqyJh4UQgEARCSDGIkadPkMAAjUJIMaaeFgIAQgUkcD/AAPBSru0RZa3AAAAAElFTkSuQmCC[/img][br]Select [b]all[/b] triangles which must be similar to triangle [math]ABC[/math].
In right triangle ABC, altitude CD with length h is drawn to its hypotenuse.
We also know [math]AD=12[/math] and [math]DB=3[/math]. What is the value of [math]h[/math]?
In triangle [math]ABC[/math] (not a right triangle), altitude [math]CD[/math] is drawn to side [math]AB[/math]. The length of [math]AB[/math] is [math]c[/math]. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWUAAADSCAYAAACSPdHCAAAgAElEQVR4Ae2dC9hVUxrHVV9pun6lh6QLSpFJRVSUQtSkxJTbkKKZ6OZLSqKeIhJPKcLIrdyakEuMEvFlGNcSMUZCuTMyERKa753nv1in3W6fc/beZ1/WPvu/nmc/Z5991l7rXb+1zv+ss/Za691FGEiABEiABIwhsIsxltAQEiABEiABoSizEZAACZCAQQQoygZVBk0hARKInsD69etlxYoVMn/+fPW6adOm6I2w5EhRtsDgKQmQQHoIQHwHDx4su+yyizratm2rXps1axYrBIpyrPiZOQmQQBwEIMjt2rUTCHF5efkOJqxevXqH91G/oShHTZz5kQAJxE6gX79+gh5x3EMVTiAoyk5UeI0ESKBoCaBnjCELew/ZlAJTlE2pCdpBAiQQCYFBgwapXnIkmfnIhKLsAxpvIQESSC4BDFuUlZUZWwCKsrFVQ8NIgATCIIChi8mTJ4eRdCBpUpQDwchESIAEkkKAopyUmqKdJEACqSCA4QuMK5sa2FM2tWZoFwmQQCgEMJ6M3nLc85GzFY6inI0Mr5MACRQlAcxNxqKR0tJStaJvypQpMnr0aLWYxIQCU5RNqAXaQAIkEDmBWbNmCRaRdOvWTb3ivQmBomxCLdAGEiABEviNAEWZTYEESIAEDCJAUTaoMmgKCZBA4QTwAA/bcSY1UJSTWnO0mwRIYAcCL7zwguy///5qZgVmV5x++uk7fJ6UNxTlpNQU7SQBEshJ4LDDDssIMkQZx9VXX53zHhM/pCibWCu0iQRIwBOBL774YidBhij37NnTUzomRKYom1ALtIEESMA3gXXr1slf/vIXR1E+99xzfacb140U5bjIM18SIIGCCLzyyivSv39/JcZ77LGHHH300TsIc40aNYxdtZer4BTlXHT4GQmQgHEEnnjiCTnqqKOUALds2VJmzpwp33//vbLz0UcflZKSEvXZq6++apztbgyiKLuhxDgkQAKxE1iwYIFaHo2x4kMPPVRuv/12R5vq1KmjRPn55593/Nz0ixRl02uI9pFAygnccMMN0rRpUyW0xx57rCxatCgnkfr166u4t9xyS854pn5IUTa1ZmgXCaSYwE8//SRTp06VWrVqKYEdMGCAPPXUU66I7L777uqeCy64wFV80yJRlE2rEdpDAikm8PnnnwvEVM8zHjJkiOCBnpeAh3716tVL5HQ4lJOi7KW2GZcESCAUAm+//bbaeB5iXK1aNRkzZoy8++67vvKCKO+3335qyMNXAjHfRFGOuQKYPQmkmQAexvXt21f1jBs1aiSXX365TJgwQdasWeMbC0S5c+fOKs0k7oFBUfZd9byRBEjALwFMXTviiCOUcLZu3Vquu+462bp1q0pu1apVMm3aNL9JC0RZC/3jjz/uO524bqQox0We+ZJACgnMnz9fIMIYpkBvFu+dwp133pl3loXTfbgGUT777LNVHjNmzMgWzdjrFGVjq4aGkUDxELj22mulYcOGSih79eolDz/8cM7CYfbFFVdcIf/4xz9yxnP6EKKMMWms6DvnnHOcohh9jaJsdPXQOBJILoHvvvtOJk2aJFWrVlVifNppp0l5ebnrAn3yyScyfvx4wZacXoIW5Y4dO6reuJd7TYhLUTahFmgDCRQRgY8++khGjBihhBjDFNgU6LXXXvNVwg0bNsill14qy5Ytc32/FmVMp6tbt65UVFS4vteEiBRlE2qBNpBAERB4/fXX1cbyEGIsdb7ooovk/fffL7hkX3/9tcyePVtuvfVW2bhxY970tCjjHtgCu5IUKMpJqi3aSgIGEnjmmWfUQg0IIJZDX3nlla7E02tRMJNi5MiRgtcff/wx6+1alJcvX65EGXtmJClQlJNUW7SVBAwigD0otLePNm3ayI033ijbtm0L1cIvv/xS7rnnHikrK5OFCxc6LjDRooy4+KHAuHaSAkU5SbVFW0nAAALY6KdFixZK8Lp27apEMmqz/vvf/wq28Jw+fbpceOGFMmfOHLn//vvV2DOWWGOvDMyFxjn2XE5SoCgnqbZoKwnESAD+7iBy6H326dNHHnvssRit2Z715s2b5a233pKnn35aHnnkEfVwD4tHlixZIp06dVLzorfHNv+Momx+HdFCEoiNAB6yYVoahBjHGWec4WvucJQF0MMXyHPs2LHKbvSskxIoykmpKdpJAhESeO+99zJ+7ypVqiTDhw8vaD8KjAF3794967F69WpVOrw6xcP91oDFJ6NHj1azMqzXcW4VZawYxI/Js88+a49m7HuKsrFVQ8NIIHoCVr93GKq45JJL5MMPPyzYkHnz5snkyZN3Ovr166dEU28chMUlEFF7XNyvAwRZv8d9dsG2ijL20UB6N998s77d+FeKsvFVRANJIHwCeGimHY/us88+gvHjb775JvSMu3Xrprbs1BlpUdbvnV7tIgwBtwarKGPqHET5/PPPt0Yx+pyibHT10DgSCJcA5vC2a9dOCVf79u0j7VFiqAKCqXvJKCkEFkKdK0CUN23alIkyaNCgzDlOrKKM9wceeKDAjVRSAkU5KTVFO0kgQAKYU9ykSRMlihjD/dvf/hZg6u6SgpjaBViLMoR6xYoVjgnpIQus2INA2zc3sovyqaeeKnvttZdjWiZepCibWCu0iQRCIKD93tWsWVOJMcZzly5dGkJO+ZOEsKKXbN+gCKKM69YDPxr6QaA1Zadr+Nwuythtzt4jt6Zj2jlF2bQaoT0kEDCBL774Yge/d+ihet15LWCT1Dhys2bNHJO1DmfgHD8epaWlOwxzON7420W7KGPuMkQZi0mSECjKSagl2kgCPghY/d6VlJSoh13/+te/fKQU7C0YD4ZI6hkU+VLX8WfNmpUvqvrcLsqY3of88PAyCYGinIRaoo0k4IGA1e9dgwYN1N4P2JvYlIAhimy95Gw2tm3bVj0EzPa59bpdlPEZtvC0PxC03mPSOUXZpNqgLSRQAAH8Pe/SpYvqFWJvCrhC+v777wtIMfhb0evFUASE2W3QPWX7A71s9zuJMvwBYvOkJASKchJqiTaSQA4CWLV2wAEHKDHu0KGD3HbbbTlix/sRhiDQa4XQOgWItfUBHsaU8aAPPeVs99jTcRLl8847T2rVqmWPauR7irKR1UKjSCA/AQgcBAjjpT169JAHHngg/00xx8CwRa5hBL3CD2XSB65ZH/7lK4KTKN9www0qvSRseE9RzlfD/JwEDCKA4QjsD4wHdxAtbEv55JNPGmRhMKagt2ztMXtJ1UmUsfcFeGEvZtMDRdn0GqJ9JCAidr938NKMfSoYdibgJMpfffWVEmXs5WF6oCibXkO0L9UErH7vqlevLmPGjJG1a9emmkm+wjuJMu7B0MlJJ52U7/bYP6cox14FNIAEdiYAv3e9evVSvTuIzGWXXSZYBMKQn0A2UT7++OOlVatW+ROIOQZFOeYKYPYkYCUAv3eHHnqoEmMICPZ3yOUk1Hovz38lkE2UL774YsX122+/NRoVRdno6qFxaSFw6623SvPmzZVodOzY0fVqt7Tw8VLObKKMh3x42JdtoyMveYQZl6IcJl2mTQJ5CGDpLxZTQCx69uy5045neW7nxw4EsokyxufBGTvkmRwoyibXDm0rSgLwF2f1e4etJTGGzBAMgWyi/PPPP0uVKlVkxIgRwWQUUioU5ZDAMlkSsBOw+r1Dj23o0KECd0UMwRLIJsrIBSsD4WHF5EBRNrl2aFtREMB84gEDBqi/ztjLeNy4cQKBZgiHQC5RPvPMM6Vhw4bhZBxQqhTlgEAyGRKwE4Dfu6OOOkqJMTxfYLP1jRs32qPxfcAEcony9OnTVX1gMY6pgaJsas3QrsQSgGsl/E3GEAX8w2HfhV9++SWx5Uma4blE+e9//7uql8WLFxtbLIqysVVDw5JGAE/1GzdurL70hx9+uNx9991JK0JR2JtLlD/44ANVP9OmTTO2rBRlY6uGhiWBAJ7oT506VWrUqKG+7L17906M26Ek8PVjYy5RRnq77babDBw40E/SkdxDUY4EMzPxSgBbNU6ZMsXrbZHFt/u9+9Of/iTYiYwhfgL5RBketA855JD4Dc1iAUU5CxhejpeAH5dBUVhs9XuHMePhw4fLG2+8EUXWzMMlgXyiPHLkSPXPxmVykUejKEeOnBm6IYCNzXGYEqx+7+rUqSMTJkyQDRs2mGIe7bAQyCfKc+fOVUNNb775puUuc04pyubUBS2xEIDLILfeiy23BX4Kv3fw74ZecdOmTQVTqty6JQrcGCboikA+UX7uuedUfd51112u0os6EkU5auLMLy8BjCdDBMvLy2X06NHqfO+99450k54777xT9t9/f5X3QQcdJH/961+loqIir+2MED+BfKL89ddfq3rFUncTA0XZxFpJuU3wWgxRhsNMjC1DnMvKytQ1L77a/GBE73z33XdXeR155JGCOccMySKQT5RRGuzId8IJJxhZMIqykdWSbqMgxBBl6/CFdjMPgQ46aL932KwG+fbt21eWLFkSdDZMLyICbkT5xBNPlBYtWkRkkbdsKMreeDF2BAQwZQmue+xBD2nYr/t9b/d7h7mr//znP/0mx/sMIeBGlCdOnKh+gH/44QdDrN5uBkV5OwueGULA3kuGWeghByXKVr93lSpVklGjRslbb71lSOlpRqEE3IjywoULVXvCQz/TAkXZtBpJuT1wK+8kvhjKwIyMQgL2LD7uuONU+vXq1RP0lj755JNCkuS9BhJwI8pr1qxR7eD66683rgQUZeOqJN0GzZs3bydRxngyZl8MGjTIF5wHH3xQOnTooNLdZ599ZMaMGfLdd9/5Sos3mU/AjShv27ZNdt11Vxk2bJhxBaIoG1cl6TYIwovxZC3AEGQ8lEEv2evMC/i9gwij592+fXvBe4biJ+BGlEEBS63x/MK0QFE2rUZSbg+2vMSUOD0FDoKKLw6GNdwG+L2DiONe7Gd8//33u72V8YqAgFtRHjx4sJr+aFqRKcqm1QjtyRBALxmHm2D3e3fSSSfJsmXL3NzKOIYTwI+yl6mQbkV55syZ6of7008/NYoARdmo6qAxXgnY/d6h9/Pyyy97TYbxDSWgH/x6+afkVpSXLl2qRBkb35sUKMom1QZtcU0Afu/++Mc/qi9VSUmJWo79zjvvuL6fEZNBAA9+vc66cSvKH374oWo/cNOVL+BHAStMMSSGA3bhCGPTLIpyvtrg50YRwJCE/nI0aNBA7bn8+eefG2UjjQmOAB746odxGMpy02N2K8qwEnGxF3augAfMpaWlSoBxjgPPPjAjCKtPgw4U5aCJMr1QCGAPijZt2qheCpbHYt7yli1bQsmLiZpDAOIH4bM++IUY5nrW4EWUe/TooWbm5CqxnhFkzdNp6mauNLx8RlH2QotxIycAv3fwBI2/jJhrjC8DQ3oIoN7btWunhBmiiAPDGbl6qF5EGbsQYr5ytoD89HCFNQ46BbhuFWrr54WcU5QLocd7QyGg/d5Vr15dNXz0Zh566KFQ8mKi5hLQS+vRS7YG3Xu2XrOeexFlzF2HuMKjjFPQNtjnyMMmp/1ZnNLweo2i7JUY44dGwO73bsCAAfL000+Hlh8TNpuA3i3Q3huFiGIue7bgRZSxARXSu/feex2T0zZYP4Q9hawwtabldE5RdqLCa5ESQC/lrLPOUl8OfEH+/Oc/y8qVKyO1gZmZR8DJJVi2nqvVei+i/M0336h2N27cOGsSmXMnUdbXrFvLZm4I4ISiHABEJuGPAPze9enTR30pMK43duxYwbxjBhIAAQwPQACtwc3GVF5EGWnDw8zxxx9vzSZzrudJz549W40fw8M6fizQefCyoCWToIsTirILSIwSLIHHHntMOnfurBo2vkBTp06Vr776KthMmFqiCegHbHbhc+o92wvqVZQxTLbvvvvak8m8t878wLkW6kyEgE8oygEDZXLZCcDvXatWrZQY43XOnDmCh3oMJGAnoF2C2ceTnXrP9nu9ijJ6v+j5bt261Z5ULO8pyrFgT1em+MuJhR5o+B07dhRTvQinq1bMLi2mPuqdAq2WutmcyqsoY8MqtM0XX3zRmlVs5xTl2NAXd8ba713lypVVg+/Zs6csXry4uAvN0hlBwKsow+sMRBlz4k0IFGUTaqGIbIDfu+HDh6tGjoZ+6qmnyrPPPltEJWRRTCfgVZQrKiqkZs2aMnToUCOKRlE2ohqSbwT83p122mkZMT733HMF1xhIIGoCXkUZ9nXq1Em6du0atamO+VGUHbHwolsCeDp+7LHHKjGuUaOGjB8/3rOHELd5MR4JuCHgR5QxN3633XZzk3zocSjKoSMuzgzg9w7udDBE0ahRI7nqqqsEG80zkEDcBPyIst7LAqtK4w4U5bhrIGH5Y68ALDGFGLdu3VpuuukmwZgcAwmYQsCPKGNLWLRpbHwfd6Aox10DCckffu/q1KmjGu7hhx8uCxYsSIjlNDNtBPyI8scff6za9rRp02LHRVGOvQrMNQDDERdddJFqrOhF9O7dWx5//HFzDaZlJPDbxvVjxozxzKJx48ZqtpDnGwO+gaIcMNBiSA77T+DBB4QYBzwzYJ8KBhJIAgE/PWWUq1evXnLQQQfFXkSKcuxVYI4Br776qsALtBZjzDfGxHoGEkgSAb+ijA2x4O8x7kBRjrsGDMgfDzmwfBViXLt2bbnkkksEY2wMJJBEAn5F+Y477lDfgbVr18ZabIpyrPjjzRx+737/+9+rhtikSRO55pprZPPmzfEaxdxJoEACfkX5pZdeUt+FhQsXFmhBYbdTlAvjl8i7scYfc4vRM4Yz0ltuuSWR5aDRJOBEwK8oo0OC7wQWQMUZKMpx0o8wb2yRefnllysnkWh4WFJ63333RWgBsyKBaAj4FWVYh3+Of/jDH6IxNEsuFOUsYIrlMlYowWMvhBhH3759BWPIDCRQrAQKEWXs3xKWQ1S3vCnKbkklLB783g0cODAjxjjHmBkDCRQ7gUJEGf8m0Xn55ZdfYsNEUY4NfTgZwzsv/I2hYVWqVElGjRol//73v8PJjKmSgIEEChHlRYsWqe/OK6+8ElvJKMqxoQ82Y/i9w/aDEOPS0lKZNGmSfPbZZ8FmwtRIIAEEChFldGDwHZo7d25sJaUox4Y+mIzh965ly5aqIWGjoJkzZ8qWLVuCSZypkEACCRQiyiguOjXYDzyuQFGOi3yB+V577bVq/1f8qrdr105uv/32AlPk7SRQHAQKFeUuXboINt2KK1CU4yLvI1/4vZs4caIaK4YYd+/eXbCvMQMJkMB2AoWKMnrJ6C3HFSjKcZH3kC/83g0bNkwNUUCMTzzxRFm+fLmHFBiVBNJDoFBRvu6669R3bePGjbFAoyjHgt1dpm+88YbaShBCjGPw4MGycuVKdzczFgmklEChovzUU0+p79uTTz4ZC0GKcizYc2cKv3c9evRQDQO7VmHxx7p163LfxE9JgAQUgUJF+dNPP1XfPTh2iCNQlOOgniVPzJE8+OCDVYNo0KCBTJkyRf7zn/9kic3LJEACTgQKFWWkiZlMWN0XR6Aox0Hdlic2BMLSTgxRNG/eXGbPni0//fSTLRbfkgAJuCEQhCj36dNHDjzwQDfZBR6Hohw4UvcJTp8+Xe1fDDGGZ+j58+e7v5kxSYAEHAkEIcpwg1a5cmXH9MO+SFEOm7Atffi9GzdunOoVQ4yPOeYYeeSRR2yx+JYESMAvgSBEGR0kfD/hGi3qQFGOiPj7778vQ4YMyYhx//79ZcWKFRHlzmxIID0EghBl7H0BUX7ggQciB0dRDhk5/N5hXjEqGAeEefXq1SHnyuRJIL0EghBlLNTCzCe4Ros6UJRDIv7EE0/IkUceqYR41113lQsvvFA++OCDkHJjsiRAAppAEKKMtLB9QRwb3lOUdU0G9LpgwQL11Ba9YjSOqVOnCsaRGUiABKIhEJQon3HGGdK4ceNojLbkQlG2wCjkdM6cObLnnnuqnnGrVq0E7//3v/8VkiTvJQES8EEgKFG+8sor1fe5oqLChxX+b6Eo+2cn8Ht32WWXSbVq1VTlHXbYYXL33XcXkCJvJQESKJRAUKL88MMPq+/1qlWrCjXJ0/0UZU+4fo0Mv3fnn3++qjAMUxx33HGCTeYZSIAE4icQlCivXbtWfcdvu+22SAtFUfaAG14JzjzzzIwYn3LKKfLcc895SIFRSYAEwiYQlCjDTmx3MGLEiLBN3iF9ivIOOJzfPP/88+oprJ7WNnToUHnzzTedI/MqCZBArASCFOVu3bpJ586dIy0PRTkH7kcffVQ6duyoesY1atQQLL3E3sYMJEAC5hIIUpSxj3mdOnUiLSxF2QH3vHnzZL/99lNi3KhRI5k2bZp8++23DjF5iQRIwDQCQYoyZlHhH/KmTZsiKyZF2YIaTkfr16+vKqF169Zy0003WT7lKQmQQBIIBCnKzzzzjNIDvEYVUi/KWE6JpZR6vBgOE7EAhIEESCCZBIIUZcy0gjbMmDEjMhipFeWPP/5YzjvvvIwY9+7dW5YsWRIZeGZEAiQQDoEgRRkWtmjRQrC6L6qQOlF+/fXX5eSTT86I8emnny4vvPBCVLyZDwmQQMgEghblE044QTCcGVVIjShjTAh7F+thCjxVffvtt6PizHxIgAQ8EMBirAcffFCwqs7rUVpaKmPGjPGQW+6oF198sdKN3LGC+7ToRRn7oWK3J4hx7dq1ZcKECfLZZ58FR5ApkQAJBE4A291ip0V4lPZ61KtXL1BRvuuuu5R+rF+/PvByOiVYtKI8d+5cadq0qYLZpEkTgWfaH374wYkBr5EACRhGYNSoUbJt2zZfVgU9fLFy5UqlIw899JAve7zeVHSijDnFNWvWVBDbtGkjEGcGEiCBZBEwSZS3bNki1atXl0mTJkUCsShEGRO7x44dq4QYwxRdu3aV++67LxKAzIQESCB4AiaJMkoHx8bwcB1FSLQow6nh2WefnRHjvn37yrJly6LgxjxIgARCJGCaKA8cOFD22muvEEu8PelEijKcGvbr1y8jxgD28ssvby8Vz0iABBJNwDRRvuqqq5TeRAE1UaK8dOlS6dKlS0aMR44cKdjzlIEESKC4CJgmyosXL1a6g3UOYYdEiPK9996rJm9jvBhzECdOnChffvll2GyYPgmQQEwETBPldevWKVHGZmVhB6NF+frrr1fORyHGe++9t1p/vnXr1rCZMH0SIIGYCZgmysDRsGFD5XEobDTGiTL83k2ZMkWqVq2qfpmw8CNqdyxhQ2f6JEACuQmYKMpHH320mtmV2/LCPzVGlLEbEyoCvWIc3bt3l0WLFhVeQqZAAiSQOAImijKeYdWqVSt0lrGLMvafwA5MWoyxvHL58uWhF5wZkAAJmEvARFHG/urQqc2bN4cKLhJRhsgOHz5cHVpw4XC0V69eGTEePHiwYDkjAwmQAAn4FWUsGvvd734nHTp0kDVr1gQK8sYbb1R6hfUQYXqvD12U77nnnozw6t5w8+bN1bUqVarI6NGjBYtAGEiABEhAE/AjypMnT95Ba6AvWNMQRMBe61q/9CtcRYURQhflTp067VSYkpIS9TAPD/R4kAHbANuAvQ3AYTFE1n491/tq1artpDVYHp3rHreftWzZcqe00bkMI4QuynA8qn9Z+PrrQ0xyIAe2geS3AcwQCyOELspDhgzZSZRxjYEESIAEgiQA/5r2Hzs4Qw4ijB8/fqe0MSkhjBC6KGMHN+sDPZxH6a47DGhMkwRIwDwCq1atkvbt22fEE5uVBRUqKiqkf//+mbSxE2VYm96HLsoayoYNGwQHAwmQAAmESeCdd94RrHsII8DhctgTEyIT5TAAMU0SIAESKDYCFOViq1GWhwRIINEEAhHlQYMGSVlZWaJB0HgzCaxevVrmz58vK1asMNNAWmUMAeiQftCHDcywVcPs2bNjsQ/7vSN/fWBxXHl5uStbChZluP/WIFzlyEgk4IIAHgajQdetW1e6deum2hh/+F2AS3GUtm3bCoQZ4octNtFeoE1oR1EGtF3kC1sw1xqHbsPQy3yhYFFu1qxZxgtIvsz4OQm4JYBGjC+ZnqmjV2u5vZ/x0kcAQmjf71h3Gu3Xw6Sj87TPztA/GvnyLkiUUVD0ZPAXE0Dcds/zGcXP000A7QjtCe1KB/wdRKNmIAEnArrN2IUQcdFu0H6iCuhAoLNqD6GLMnow8AICAxAoyvYq4Hu/BPC3D20LS2CxNwr21NY//n7T5H3FTQA6hDbiFPCvC0dUAXnZfwTQgXWrkb57yvZfAwDRAh1V4ZlPcRJAo0ZPA69oU1H+9SxOosVfKohgNuHF9WyfhUEGWqgfNGI8G50K5O92JMGXKOtesvXLgkwpymFUcfrShCCzLaWv3gspca42g8/w7yuKgOET9IjtD/kgzNbhuFy2+BJlZIiM7UeUv0a5CsXPkk0A7SjqJ+bJJpZu67UQOvVE9fMuawcyTFp6mMKeB9q0fUjDHke/9yzKGsCsWbNUdxwgcECoKcoaK18LIYD2hB98zO3EPFOMLePvIAMJOBHQsx30TB1rHGhStrFma7ygzjENz+mBNP75ubXDsyijkE7iC5HGF4mBBIIgAGHW44T4wXczvzOIfJlG8ghA8DBEYQ/6Hz3aUlQB2oh87QFC7aSb9nh470lFdQ/GqZD6M6dMeI0ESIAEwiIAscNwF1Z94tD/rNAzjfrHHB1TPVSCnjvswRafuB7KmDIKn03ttSg7CXZYlcF0SYAESADiC9HDgR4zNAr/3J2GM8KkpcevtS36Ff/4vOiip55ymAVi2iRAAiRAAh6HLwiMBEiABEggXALsKYfLl6mTAAmQgCcCFGVPuBiZBEiABMIlQFEOly9TJwESIAFPBCjKnnAxMgmQAAmES4CiHC5fpk4CJEACnghQlD3hYmQSIAESCJeAsaKMid9RT/4OFzVTJwESMI2AiTpjnChjWSQ2onFaP25ahSdVjDQAAAKfSURBVNIeEiCB5BOA1mApNBz0mtARNEKUtRDXrl1bLZXMtpQ7+dXPEpAACZhIQG9ehKXRcQt0bKJsF2K9Thy7KZnwa2Viw6FNJEAC4RGwCrPWozgEOlJRtgtx5cqVMxuJAEK1atWkadOmau9c7J/LgwzYBtgGomwDtWrV2kGTSkpKMu+1QIf3s/BrypGKMnrA2NYOuybpXyKrMFetWlVOPvlkGTZsGA8yYBtgG4i0DZxzzjlSv379jDZVqVIlcw7NgnZF8S8+UlG2/sI4CTSEGuPKbvcdtabHcxIgARLwSwB61KZNm4wIQ4uiFGKr3bGJstUIu0DDvTyF2UqI5yRAAmERgP7AsWmcQmwtmxGibDVICzQG3SnMVjI8JwESCJoA9AbupKIamnBjv3Gi7MZoxiEBEiCBYiVAUS7WmmW5SIAEEkmAopzIaqPRTgTWr1+vVoPCiSYO7cDSKS6vkYCpBCjKptYM7fJEAAJsfVCDcUI4z2QggaQRoCgnrcZo704E8LAGM3YgxAwkkHQCFOWk1yDtl7KyMuVanihIoBgIUJSLoRZTXgbsl4IplAwkUAwEKMrFUIspLwPGkjl0kfJGUETFpygXUWWmtSh169alKKe18ouw3BTlIqzUtBUJexRgmSwe+OlgPdfX+EoCSSBAUU5CLdHGnAQwP7lZs2ZqBgbmJ2OrRw5n5ETGDw0mQFE2uHJomnsC6BmXl5cL9uzmninuuTGmeQQoyubVCS0iARJIMQGKcoorn0UnARIwjwBF2bw6oUUkQAIpJkBRTnHls+gkQALmEaAom1cntIgESCDFBCjKKa58Fp0ESMA8AhRl8+qEFpEACaSYAEU5xZXPopMACZhHgKJsXp3QIhIggRQToCinuPJZdBIgAfMI/B/LlpLLH4PieQAAAABJRU5ErkJggg==[/img][br]Which of the following statements must be true?
Quadrilateral [math]ABCD[/math] is similar to quadrilateral [math]A'B'C'D'[/math]. Write 2 equations that could be used to solve for missing lengths.
Segment A'B' is parallel to segment AB.
What is the length of segment [math]A'A[/math]?[br]
What is the length of segment [math]B'B[/math]?[br]
Lines [math]BC[/math] and [math]DE[/math] are both vertical. What is the length of [math]AD[/math]?[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAASwAAADbCAYAAADXnaxgAAAgAElEQVR4Ae2dDbhNVf7HKaRCkqFb3tLUI2GuxJS3MNT0mHky8RSNt0pImOSlvETek0yFBqWickkK1dCMt2QUooy3pGjoFlEjyS3C7/981/zP6br3nH32Pmfvvdbe+7ue5zzn3L3XXuu3vr99Pnedtdf6rSLCRAWoABUIiAJFAmInzaQCVIAKCIEVwpvg5MmTsmDBAlm3bl0IW8cmuaHAiRMnZN68efLBBx+4UZxvZRBYvkntX0V5eXly/fXXy7Bhw/yrlDUFSoEjR45Idna2jBw5MlB2E1iBcpc9Y3/88Udp2bKljBkzxt4FzBU5BY4ePSqNGjWSCRMmBKrtBFag3GXPWALLnk5RzkVgRdn7hrWdwDLMIQaaQ2AZ6JSomkRgRdXz9ttNYNnXijk9VoDA8ljgEBRPYIXAiWFpAoEVFk961w4CyzttWbJDBQgsh4JFMDuBFUGnm9pkAstUz5hjF4Flji8ibwmBFflbIKUABFZKiZjBLwUILL+UDm49BFZwfRc6ywms0LnU9QYRWK5LygLTVYDASle56FxHYEXH18a3lMAy3kXaDSSwtLuABsQUILBiSvA9mQIEVjJleNx3BQgs3yUPXIUEVuBcFl6DCazw+tatlhFYbinJcjJWgMDKWMLQF0Bghd7FwWkggRUcX+mylMDSpTzrLaQAgVVIEh4ooACBVUAQ/qlPAQJLn/ZBqZnACoqnImAngRUBJ2fYRBOBdfr0acGOT1aJMd2t1AnoOQIroI7z0WzTgAVQ9e/fX9auXWupAoFlKU8wTxJYwfSbn1abBKxt27ZJ06ZNpUyZMin30iSw/LxLfKqLwPJJ6ABXYwqwJk+eLEWKFJFmzZrJjh07UipKYKWUKHgZCKzg+cxvi3UDa+vWrVK3bl0FK+xSbjcRWHaVClA+AitAztJkqi5gff/99zJp0iQ599xz1Wa/X375pSMFCCxHcgUjM4EVDD/ptFIHsJYvX67GqqpWrSpPPPFEWs0nsNKSzeyLCCyz/WOCdX4C68SJEzJu3DgpWbKkdOjQQXbu3Jm2BARW2tKZeyGBZa5vTLHML2Bt375drrrqKilVqpTMmTMn5TyrVPoQWKkUCuB5AiuATvPZZD+ANWrUKDWo3qpVq4xBFZOHwIopEaJ3AitEzkyzKZg1bpW8BBamJ1xxxRVSunRpefXVV63McHyOwHIsmfkXEFjm+8hLC/ft2yfjx4+X3r17S9++faVnz54yffp0ycvLi1frBbAOHz4sI0aMkBIlSkibNm1k//798frc+kBguaWkQeUQWAY5Q4MpOTk5Ur16dQWqfv36Sa9evWTGjBmC+yKW3AbWqlWrpEGDBpKVlSULFy6MVeP6O4HluqT6CySw9PtApwUPPfSQ3HHHHZYmuAks9OIuvPBC6dixY0ZPAC0N/v+TBJYdlQKWh8AKmMNcNvePf/yjTJw40bJUN4C1YcMGqVy5sloDuHjxYsv63DpJYLmlpEHlEFgGOcNnU3JzcyU7O1sArUGDBqlxrClTphSyIlNgDR48WD0BvOuuu+TYsWOFyvfqAIHllbIayyWwNIqvuer169dLrVq15Oabb5YuXbpI+/btE84qTxdYS5cuVfOqzj77bFm2bJnvrSWwfJfc+woJLO81NrWGV155RVq0aCEAklVyCqwvvvhCBg4cKOXKlRP0qr7++mur4j07R2B5Jq2+ggksfdrrrhkD7lj+curUKUtTnABr0aJFcuWVV0rt2rXVbHXLgj0+SWB5LLCO4gksHarrrxMQwtjV1KlTUxpjB1jI06dPHzVWdf/998uhQ4dSlut1BgLLa4U1lE9gaRDdgCr37t0rFSpUUIBBULzY6/jx44WsSwWsjRs3Svny5dVs9TVr1hS6XtcBAkuX8h7WS2B5KG5Iik4GLPSiOnXqpGDXrVs341pLYBnnkswNIrAy1zDsJSDkC8ISx+JSYcxr5cqVcumll0qNGjVkxYoVRkpAYBnplsyMIrAy0y8KVwNIlSpVkjvvvFO2bNkiPXr0UD//sIzHhLGqZD4gsJIpE+DjBFaAneeD6bt27ZKyZcuqn30Iqodxr/r166selg/VZ1QFgZWRfGZeTGCZ6RdTrBowYEB8QD42MP/ee++ZYp6lHQSWpTzBPElgBdNvflmNsasYqPBerFgx2b17t1/VZ1QPgZWRfGZeTGCZ6RfdVmGdYZ06dRSsEH4mBi1MNk009UG3vYnqJ7ASqRLwYwRWwB3osvl4Ijh69GgFqIoVK8pf//pXOXLkiPq7e/fuLtfmbXEElrf6aimdwNIiu5GVYrHyjTfeqOCEJTuffvqpshPAOuecc2TIkCFG2p3MKAIrmTIBPk5gBdh5Lpo+dOhQBSqACYuif/7553jp//3vf6V48eLy4IMPxo8F4QOBFQQvObSRwHIoWMiyYxv42FhVy5YtEy6EJrBC5vQgN4fACrL30rcdO+U89thjqleFAXXMXE+WCKxkyvC47woQWL5Lrr1CBO5DuGKAqm3btimjgBJY2l1GA2IKEFgxJcL/jqkK06ZNU6C67LLLZP78+bYaTWDZkomZ/FCAwPJDZf11rF69WurWratghWigWHJjNxFYdpViPs8VILA8l1h7BVisjJ9/WAuIqQtOE4HlVDHm90wBAsszabUXjPlTRYsWVbBC3CrEtUonEVjpqMZrPFGAwPJEVq2FIl4VAuqhV4WYVen0qvI3gMDKrwY/a1WAwNIqv+uV//Of/1RbzwNW2F3ZjURguaEiy3BFAQLLFRm1F3L48GHBWj+ACnsNzpo1yzWbCCzXpGRBmSpAYGWqoP7rX375ZbW1FmB13333ycGDB101isByVU4WlokCBFYm6um/Fjs2A1RYA/jRRx95YhCB5YmsLDQdBQisdFTTfw0G0gEpwOq2227z1CACy1N5WbgTBQgsJ2rpz/v555+rTSAAqipVqsjmzZs9N4rA8lxiVmBXAQLLrlL68y1btizeq+rfv79goN2PRGD5oTLrsKUAgWVLJq2ZsIymZ8+e6udfdna2rFq1yld7CCxf5WZlVgoQWFbq6D83b948ycrKUrCaOHGi608A7bSQwLKjEvP4ogCB5YvMaVXSpEkTBaoyZcoIQsLoSgSWLuVZbyEFCKxCkmg/gLEqDKrjNWrUKO32EFjaXUADYgoQWDEl9L8jXlWbNm0UqBo1auT7WFUyBQisZMrwuO8KEFi+S56wwsmTJ0u5cuUUrPr27Zswj66DBJYu5VlvIQUIrEKS+Hpgz5490rp1awWq5s2bW8ZW99WwfJURWPnE4Ee9ChBY+vR/8sknpXTp0gpWI0aMMHZHZQJL3z3CmgsoQGAVEMSHPw8cOCCNGzdWoMLPQNMTgWW6hyJkH4Hln7OxOens2bMVqPAEELHVg5AIrCB4KSI2Elj+OHrjxo3xbeAbNmzoaBMIfyxMXguBlVwbnvFZAQLLW8Hz8vJk5syZcvbZZ6v46jNmzBAAIEiJwAqSt0JuK4HlnYM//vhjwZM//Pxr0KCB7Nixw7vKPCyZwPJQXBbtTAECy5lednNPmDAhPlb16quvyk8//WT3UuPyEVjGuSS6BhFY7vs+FlgPvap9+/a5X4HPJRJYPgvO6pIrQGAl18bJmWPHjgmiKeDnHxYrP/XUU04uNzovgWW0e6JlHIGVub/XrVsXH6tq27atbNq0KfNCDSqBwDLIGVE3hcDK7A7o06ePFCtWTG0Dj3GrMCYCK4xeDWibCKz0HId5VYj+iZ+At9xyiyDWelgTgRVWzwawXQSWc6cNHz48/gRw2rRpzgsI2BUEVsAcFmZzCSz73l29erVUqFBBwapmzZr2Lwx4TgIr4A4Mk/kEVmpvfvXVVzJlyhQFqksuuUQQuypKicCKkrcNbyuBZe0ghCuuXbu2glW7du1CPVaVTAkCK5kyPO67AgRWYsm/+eYbGTp0qAIV1gFia62jR48mzhzyowRWyB0cpOYRWIW9tXv3bqlWrZqCVYsWLQTxq6KcCKwoe9+wthNYZzrk9ttvV6AqWrSorFmz5syTEf2LwIqo401sNoElcuLECcHAevHixRWs2rdvr2XDUhPvD9hEYJnqmQjaFXVgYazq3nvvVaCqVKmSiggawdvAsskElqU8POmnAlEGVk5OjtSrV0/B6i9/+Utg41V5fb8QWF4rzPJtKxBVYP3hD39QoCpbtqy89NJLtvWKYkYCK4peN7TNUQPWm2++KeXLl1ewwgA7U2oFCKzUGjGHTwpEBViI+NmpUycFqhIlSsg777zjk8LBr4bACr4PQ9OCKABr3rx5ct555ylYtWnTJjS+86shBJZfSrOelAqEGVjbt2+Xfv36KVBhec2CBQtS6sEMhRUgsAprwiOaFAgrsPAEsEqVKgpWffv2ldzcXE0KB79aAiv4PgxNC8IGrIMHD8qtt96qQIXgenv37hXsuMyUvgIEVvra8UqXFQgTsFauXBkHVZcuXQK9tZbLbs6oOAIrI/l4sZsKhAFYeAKILbXQo8Ki5bBtAuGmv9Mpi8BKRzVe44kCQQbWDz/8oAbSMU0BsBo0aFDgtoH3xKkuF0pguSwoi0tfgaAC65NPPhFsqQVQXX311bJw4cL0ReCVlgoQWJby8KSfCgQRWKNGjZKKFSsqWI0cOVJFWvBTs6jVRWBFzeMGtzdowGrUqJEC1cUXXywYZGfyXgECy3uNWYNNBYICrNgmEPgJ2L9/f5utYzY3FCCw3FCRZbiigOnA2rx5s7Rs2VL1qmrUqCHr1693pd0sxL4CBJZ9rZjTYwVMBRYme6JXddZZZwk2gUC8KiY9ChBYenRnrQkUMBFY7733nmCRMn7+NWnSRNauXZvAch7ySwECyy+lWU9KBUwD1sSJE+WCCy5QsJo0aZIcPnw4ZRuYwVsFCCxv9WXpDhQwBVgAU506dRSoEAX022+/ddAKZvVSAQLLS3VZtiMFTADW2LFjFajwE3D8+PGO7Gdm7xUgsLzXmDXYVEAnsHbt2hVfA9i0aVOuAbTpM7+zEVh+K876kiqgA1jY8h0z1NGjwuvpp5+WvLy8pDbyhF4FUgHr3XfflSFDhsjQoUPV6+GHHxYc052K6DaA9buvgN/Awo2MJ38AFbaBX758ufuNYomuKmAFrJMnT6r4Y9dcc43a3/Huu++W7t27y9tvv+2qDekURmClo5rh1/gJrNiGpYAV5lghLAyT+QpYAQs9Y0zsfeGFF1RDTp8+LadOnRK8604Elm4PeFC/H8Datm2bVK1aVfWq8J/4P//5jwctYZFeKWAFLJzDdmn/+Mc/vKo+7XIJrLSl038huu6JkpfAQtkjRoxQoCpatKg8+uijiUzgMcMVsALWZ599JjfccINgY1qsRujatatg78dk95ufTSWw/FTbpbo+/PBDeeKJJ+Suu+5SYwxz586VEydOxEv3ClhvvPGGZGdnK1jddNNNgl4WUzAVsAIW7h/EInvuuedk0aJFMmbMGEEkDbzrTgSWbg84rB9wuuKKK6Rdu3YybNgwBaxHHnlE8JQultwGFiZ8xp4AYsY6ZqtzE4iY2sF8twJWoha9/vrraseiAwcOJDrt2zECyzepM68I/+3KlSsnr7322hmFYUA0f3ITWHjiV69ePdWrat26tezZsyd/VfwcUAWcAmvnzp1qzHL//v1aW0xgaZXffuV4+nbttdfKwIEDU17kFrAeeOABBSo8AZw/f37KepkhOApYASv/8EKsRdhmrXnz5rE/tb0TWNqkd1bx4sWLpXr16raexmUKrN27d0vJkiUVrBo3bmzE42xnajF3KgWsgIWor5dccokar0SEjaysLKlZs6YcOXIkVbGenyewPJfYnQoQ8xyhhL/77ruUBaYLLIxVDRgwQIEKg6zPP/98yrqYIZgKWAELLTp06JDavWj69Ony0UcfGdNIAssYV1gbMnz4cPWTEDdaquQUWJgQuGLFCqlVq5aCFTYs3bp1a6pqeD7ACqQClqlNI7BM9UwBux5//HE1+P39998XOFP4TyfAwtPFbt26KVCVLl1aXnzxxcIF8kjoFCCwQudSsxqECJ0XXXSRTJ06NaVhdoG1YMECNS6GQfUOHToIngQxRUMBAisaftbaSqztAlwQD71+/fqC3ZFnzpxZyCY7wOrYsaMqC+Xl5OQUKoMHwq0AgRVu/xrTOmzljvjoc+bMkWST+KyAhRnMxYsXV7DC5FOmaCpAYEXT70a2GnO2WrVqJePGjYvbh6kKvXv3VqCqVq2aTJ48OX6OH6KnAIEVPZ8b22JM/GvWrJkg6BoS1oRVqVJFwQpPAHNzc421nYb5owCB5Y/OrCWFAsePH5cHH3xQTfysXLmyGkzHOBUmAmLxcqJZzCmK5OkQKkBghdCpQWzSkiVL4oPpABVemK3MwHpB9KZ3NhNY3mnLkh0oMHr06ELA2rBhg4MSmDUKChBYUfCywW3ETz2sAcM28LGeVezdYLNpmiYFCCxNwrNaEWyt1blzZwUqhILp0aOHYOPSSpUqGbFxAH1kngIElnk+Cb1FWAP47LPPCgbX0ZtCkL0vv/xSjVdhYmmvXr1CrwEbmJ4CBFZ6uvGqNBVAqA+EKQao0JNaunRpvCRAq27dunLPPfcYEYc7bhg/GKMAgWWMK8JvyKxZs+LjVP369RPMbM+fCKz8avBzIgUIrESq8JirCiAW1nXXXadgdfnll8v69esTlk9gJZSFB/MpQGDlE4Mf3VUATwCx9Tu21cJPQAyqWyUCy0odnoMCBBbvA08U+Ne//qV2yAGosB08NqJIlQisVArxPIHFe8B1BbD34Pnnn696VUOGDLEdU5vAct0VoSuQwAqdS/U1CIH0EG0BvSrsQYhIC5jCYDcRWHaVim4+Aiu6vne15c8884wCFWCFJ4DpJAIrHdWidQ2BFS1/u95azFa/+uqrFaxq164tX3/9ddp1EFhpSxeZCwmsyLja3YZiay1ED0WPCuNVY8eOLTSvymmNBJZTxaKXn8CKns8zbjGiKMTGqjBr/f3338+4TBRAYLkiY6gLIbBC7V73Gzds2DApVaqU6llh5rqdDVLtWkFg2VUquvkIrOj63lHLsa8gnvzhJyDGqrzYVZfAcuSSSGYmsCLpdmeNRox1gAqvGTNmOLvYQW4Cy4FYEc1KYEXU8XaavXHjRsnOzlagwpjVp59+aueytPMQWGlLF5kLCazIuNp+Q/HzL9arQkC92C429ktILyeBlZ5uUbqKwIqSt2209a233pKGDRuqXtVtt93myVhVMjMIrGTK8HhMAQIrpgTfZfDgwfGxKkQE9XtrLQKLN2EqBQisVApF4Dye+P36179WsMITQF2JwNKlfHDqJbCC4yvXLcUcKmxeiqd/55xzjsyePdv1OpwUSGA5USuaeQmsaPpdNm3aJFlZWQpWt9xyS0ZrAN2SkMByS8nwlkNghde3CVuWm5sbfwKIbeCxHvDkyZMJ8/p90A6w1qxZI9OmTZOcnBz56quv/DaR9WlWgMDS7AA/q3/77bflN7/5jepV/fnPf1b7AvpZf6q6rICFG7Vdu3bSokUL9XDg9ttvl2bNmsmWLVtSFcvzIVKAwAqRM62aAkBhrArx1ZcsWSKnTp2yyq7lnBWwYC+Au2fPHtUjPHz4sGDaRe/evR0FCdTSMFbqmgIElmtSmlnQjh07FKgAq7Zt27q6WNntFlsBK1Fdo0aNkk6dOsnPP/+c6DSPhVABAiuETkWTfvjhB+nWrZuC1aWXXioLFiwwvqVOgIX23XjjjfLoo48a3y4a6J4CBJZ7WhpT0iuvvCLVq1dXsMJYD5baBCE5AdaTTz4pv/vd72Tv3r1BaBptdEkBAsslIU0oBl/47t27K1BhIujzzz9vglm2bbALrKeeeko9PMDibKZoKUBghcTfc+fOlapVqypY9ezZUw4cOBC4ltkB1nPPPafmj61YsSJw7aPBmStAYGWuodYSMODctWtXBSoMrK9du1arPZlUngpYmIlfvnz5TKrgtQFXgMAKsAMxPQGQwuvWW28NcEv+Z7oVsNCDRDs7d+4s999/v6AXec8998jAgQPl4MGDgW87G2BPAQLLnk5G5frss88kNq/qyiuvlGXLlhllX7rGWAFr9erVMmDAAOnRo4cCFWB19913q2MEVrqKB+86AitAPkO4l7///e9Srlw51dvAhqWZ7ANoWtOtgGWarbRHjwIElh7dHdf6+eefyx133KFAhc0g3n33XcdlmH4BgWW6h/TbR2Dp90FKC1588UW5+OKLFaywzVZYfwIRWClvhchnILAMvwWuu+46Bapf/epX8sEHHxhubWbmEViZ6ReFqwksA718+vRpFT4l9gQQQfaikAisKHg5szYSWJnp5/rVn3zyiYpCAFjVr19fojRBksBy/XYKXYEElkEuffzxx9UTQISAwfyiqEUhILAMuhkNNYXAMsAxu3fvlt///vdqrOr6668P5RNAOzITWHZUinYeAkuz/6dPny7nnXeegtXw4cONDKznl0QEll9KB7ceAkuT77DtO3pTGKu68MILNVlhVrV2gYWHErGXWS2gNV4rYBdYpt0fRdwUZtasWWqJx7fffutmsQnLOnr0qMycOVOBqlixYio+ecKMETxoB1gjRoyQLl26SJ8+fdTypHHjxgluYqZoKJAKWAiljXsEy7buu+8+dY8gwkdeXp5WgVwDFp7KYfeYatWqCcIJe5k2b96sgs6hV3XDDTcI/mb6RQE7wIJ2iDKK+O5PP/20XHDBBTJ06NBfCuGnUCuQCliI+X/ZZZfJ5MmT1TK2/v37S6VKlaRXr15y/Phxbdq4BqwHHnhA6tatq3ZjWbdunScNOnbsmBKwdOnSqmcF4vvRm/OkMR4WmgpYO3fuVPrlNwGbUNx88835D/FziBVIBazXXntNrrnmmjO+XwgPDmjpDPjoCrAAjfPPP1/NdWrZsqX6r+22r9GDw3ZU6BkAjBi7YkqsQCpgvfTSS+rGi12N/RSvuuoq9RMgdozv4VYgFbDGjh0r+C7nDwse+xX15ptvahPHFWA1adJE0MNCatiwoSAWuptp/PjxClSAFb5sGAhkSq5AKmANGjRI6YkpIA0aNJA6derI3/72N61d/eSt4RkvFEgFrDvvvFONR+evG+GYsBZ34cKF+Q/7+jljYOHnH0CCXtZPP/0k2KwBkzXdSIcOHRLsVIPymzZtKvgiMqVWIBWwEPsL23pNnTpVHnvsMWnUqJEMGTIk0lNBUqsarhxWwML9k52dLfPnzz+j0R9++KHaA0BnNN6MgVWjRg31c6JixYqC11lnnSV9+/bN6OZHN3TChAkKVGXKlBHs7MJkXwErYCG8Dn6+4z2WsGwJfkSXnykaClgBa9OmTdK4ceNCYcKxggS98X379mkTKSNg4ekStsHC3nboYf3444+CTTlvuukm9TmdVq1cuTL+BBA7Em/YsCGdYiJ9jRWwli5dqp7kojccS2+99Zb6p7Nr167YIb6HXAErYGGMCsM8+/fvj6uwfPlyqVy5snroFT+o4UPawMrNzVW7y8yZM+cMs3NychSFsQW604RxsOLFi6sZ6+xVOVXvl/xWwMI/FNyM6GFh+smzzz4rNWvWVPHddT6u/sV6fvJDAStgYZggNl0IvW/Mw6pQoYIghlz+f3R+2FmwjrSBNWPGDPUUoSCY8Pu2efPmZzwOLVhpwb8xjwqPUDFWhUfrYQpXXLCtfvxtBSzcdFWqVFFd/t/+9rdq7SUeZCBsNFN0FEgGLAAJc64wnxL3B1733nuv4GciJpPqTmkDyy3DMZsWoMILXxymzBWwAlbmpbOEMCiQDFimt81XYOX/ybFmzRrBrsoAFaKBMrmnAHqo6LFi92omKpBIAUzCxvBL0FY3+AIsrD9CPHVsKTVp0iSZOHGiAhWA9cILLyTSk8cyUACPoxEKGk90dM5KzqAJvNRjBTBXMjYEo/Opn9Nm2gYWxqrwJBBdSbsvXIMXHofGfvbF3jFpEVP9v/jiC9m6dav8+9//5itDDbZt26bmzmAqSExnzGPbsmWLelFj3mPbt2+X119/PX5/4D7BADtiyR05csT2d9suA5zkw7zLVME2bQML0/Qxzwpriey+8Bi0atWqat5P7AsUe8eM2aysLBUZFGFh+Mpcg4suukjOPffcM25G6A1tsQcjNc5c46BrWL58eUF0k9j3MPaO7yIextj9bnuRr1SpUoLpE1bJNrBWrVolixYtEszRsPPC3B7s+ffGG2+ouVoxYWLvmBiKQHt8uafByJEj5U9/+lOhm/Ghhx6SRx55hFrzfhOsEcSqkdj3EO8lS5ZU01uWLFli67tt5/ufTh784ko1Q8A2sKyol+wcoIX/7KD35ZdfHhfp/fffT3YJj2eoANZZduzYMa415l0xUYGCCuBnIGCFVQ+zZ88ueNrYvz0BFijZtWtXJcjDDz8cX6y8d+9eY4UIm2FYbYB4V0xUIJkC1157rfaZ68lsS3bcVWDhv/szzzyjpisgXAl7Uslk9/Y4Jv+1atVKdf+9rYmlB1UBLKfDigfMag9Scg1YCD2BSA0Y1Bs9erRgxD/oCV98jMNhlXqqpxcmtRVrOvGQZMyYMSaZRVsMUgAhxhGlA2PJQUquAAtzqUqUKKEmgL7zzjtBan9CW9FTxE9ZjLshzAYmYeIJhtehnxMak8ZBAisN0SJ2SSSB9d1338WfSmEyaJgSYp3jJy2icSJNmTJFhc4JQhsJrCB4Sa+NkQPWyy+/rL7ACAaHyZ9hT/jJi6cqiFJheiKwTPeQfvsiAyyM52CuT9myZQO3DsnpbYIIBgcPHhQ83URQwtatWzstQkt+AkuL7IGqNPTAwqAzdqnBGjUM6Hq1M44pXkd7sYShQ4cO6qkn5pNhaVIQEoEVBC/ptTH0wGrXrp0aeMa6QDwSDXtC7J+PP/5YEKETE2AHDx6sZgjHxrRMbj+BZbJ3zLAt9MDCDrDYXDHKCXmyQ2gAAADUSURBVGNYixcvNl4CAst4F2k3MPTA0q6wAQYAWHPnzjXAEmsTCCxrfXhWhMAK0V2AQIPYqgxBBhG+GWGfO3fuLLVq1QpEKwmsQLhJq5EEllb53a0c41SYtV+vXj0V+xyr29u3by8HDhxwtyKPSiOwPBI2RMUSWCFyZqwp6Gl98803sT8D8w5gYSMQLJFiogKJFIgBK2gL5F1ZmpNIEB7TpwA2om3btm3gFrbqUyx6NWOVCkJoIz5WkBKBFSRvObAVvSxu3eVAsAhmRS8r/8YwQZDg/wBva/aqwobk0wAAAABJRU5ErkJggg==[/img]
Triangle [math]DEF[/math] is formed by connecting the midpoints of the sides of triangle [math]ABC[/math]. Select [b]all [/b]true statements. [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAVoAAADxCAYAAACK/X/vAAAgAElEQVR4Ae2dCdhVU/vGlSaRBqVP0SBRSkpCZUqlQoZoUCGRkCipKA2KNNAsJZVUCg0U+YqofKYU8qfSgGg0hVJIrf/1W9+3jvMe55z3DHvez3Nd53rfc87ea7jX3vdZ+1nPup8jlJggIAgIAoKArQgcYWvpUrggIAgIAoKAEqKVi0AQEAQEAZsREKK1GWApXhAQBAQBIVq5BgQBQUAQsBkBIVqbAZbiBQFBQBAQopVrQBAQBAQBmxGwjGi/+uortXz58sjL5nZL8YKAICAI+AYBy4j2nnvuUUcccUSOV4UKFdTHH3/sGzCkoYKAICAI2IGAZUR70UUXqZtuuinSRma4Z555pipWrFjkM/lHEBAEBIEwImAZ0TKbnTZtWg4MR40apWe4OT6UN4KAICAIhAwBS4j2rbfe0oQa6ybAnVC0aNGQQSrdFQQEAUEgJwKWEG3szBXCHThwoCbfBQsW5KxR3gkCgoAgEDIELCFafLOxC2E1a9ZU+GnFBAFBQBAIOwKWEG358uXVgAEDIljiSmAhDLIVEwQEAUEg7AhkTbR79uyJ6yIwflv+igkCgoAgEGYEsiZaQ6ixbgLzuRBtmC8v6bsgIAiAQNZEi8sA10Gs4beViINYVOS9ICAIhBGBrIn2qquuUuwAI8rAvHgPycpsNoyXlPRZEBAEYhGwhGjZFWZexM4S7oXvVkwQEAQEAUHAAteBgCgICAKCgCCQHIGsZ7TJi5dvBQFBQBAQBHIl2m+//Va99tpraufOnYKWICAICAKCQAYIJCXa/v3759jxNWTIkAyqkFMEAUFAEAg3AgmJdtWqVTlI1myxXbduXbgRk94LAoKAIJAmAgmJdsyYMXGJdurUqWlWIYcLAoKAIBBuBBIS7aJFi+ISbenSpdXcuXPDjZr0XhAQBASBNBBISLSU0axZsxxkW7ZsWdW6devIZ4MHD06jKjlUEBAEBIFwIpCUaIEEV0HXrl1Vv379FEQ7fPhw9cknn6h7771XlSxZUpNu27Zt1a5du8KJoPRaEBAEBIFcEMiVaKPPnzJliibWFStW6I+///579dhjj6kaNWroz2vVqiXbbqMBk/8FAUFAEMhEVKZnz56qSJEi6vfff88B4OzZsyOuhkKFCqkJEybk+F7eCAKCgCAQVgTSmtEC0oEDB1Tz5s1Vo0aN4mK2cuVKdeutt6r8+fPrWS5uh4MHD8Y9Vj4UBAQBQSAMCKRNtIBCTrDKlSurvn37JsRo8+bNig0PKHkRg9uwYUP16aefJjxevhAEBAFBIKgIZES0gPHcc89pAl24cGFSbJgBT5o0SdWvX18fX6ZMGfX8888nPUe+FAQEAUEgSAhkTLSAYLbo7t69OyVMXnnlFdWqVStNuMxyo/OMpVSAHCQICAKCgA8RyIpo6S/EWadOnbS6/tFHH6lu3bqpEiVKaNKljG3btqVVhhwsCAgCgoBfEMiaaDds2KDDu+666660+8xMeMSIEeqMM87QhMvf119/Pe1y5ARBQBAQBLyMQNZES+deeuklVbBgQTVjxoyM+4rPt0mTJppwKWvs2LEZlyUnCgKCgCDgJQQsIVo6NHToUE2SGzduzKp/y5cvVx07dlT58uXT5d1xxx06pCyrQuVkQUAQEARcRMAyoqUPHTp0UKeeeqol3dm0aZPe9kuGXRbOyEmGb1dMEBAEBAG/IWAp0X7zzTfqvPPOUzfccINlOBAe9uSTT6q6detqwkU9bNasWZaVLwUJAoKAIGA3ApYSLY1dsmSJKlasmBo/frzlbSdm97rrrtOEyyw32YYJyyuXAgUBQUAQyBABy4mWdhjR8A8//DDDZiU/bc2aNYq05hA6hNuiRQu1devW5CfJt4KAICAIuISALURLX1jE4jHfTkOacdiwYapatWqacKtWraoTSdpZp5QtCAgCgkC6CNhGtEgoNmjQQF155ZXptimj42fOnKkuvfRSTbgFChRQI0eOzKgcOUkQEAQEAasRsI1oaejbb7+tTjjhBPXII49Y3e6E5b311lvq5ptvVnnz5tWk26lTJ7V3796Ex8sXgoAgIAjYjYCtREvjJ0+erAnvjTfesLsvOcr/4osv9GLZSSedpOtH1IbMvmKCgCAgCDiNgO1ES4d69OihEAPft2+f0/1T+/fv1yLkhJ2xcHb88cer6dOnO94OqVAQEATCi4AjRAvBXnbZZXrTgZtQv/zyyzpCAcLl1bt3bzebI3ULAoJASBBwhGjBcvXq1erkk09WvXr1ch1aws7I/FC0aFFNuCzYbdmyxfV2SQMEAUEgmAg4RrTAR2QAM8l58+Z5As2dO3dqjYbTTz9dt+u0005TixYt8kTbpBGCgCAQHAQcJVpge/DBBzWpeU1/9tlnn9V50PghQNCGtOpigoAgIAhYgYDjRHv48GG9jbZmzZpWtN/yMpYtW6ZuuukmlSdPHv2DQKjYnj17LK9HChQEBIHwIOA40QLtunXrVPXq1VXnzp09izThYX369FFly5bVhHvuueeqd99917PtlYYJAoKAdxFwhWiBY/78+VosfOrUqd5FRykdHoZAzjnnnKMJt1SpUmrKlCmebrM0ThAQBLyFgGtECwzsGMMn+vnnn3sLlQStWbBggbrmmmt0m2k38cFigoAgIAjkhoCrREvj0K6tWLFibu301PfsMOvSpYsqUqSIJl1ihHE1iAkCgoAgEA8B14n2q6++0ll027RpE699nv6M8LAhQ4aoKlWqaMKtXLmyYtYrJggIAoJANAKuEy2Nee2117S27KhRo6Lb5qv/2dbbsGFDTbhHHnmkJmBfdUAaKwgIArYh4AmipXeQLH5Pv6/sI56DO4S+8OJ/JCPFBAFBILwIeIZoGQLCvUqUKBGI0diwYYO6//77VZkyZTThErWwcuXKQPRNOiEICALpIeApot29e7cWnmnWrFl6vfDw0b/99psaN26c9kMzwy1ZsqSaNGmSh1ssTRMEBAGrEfAU0dK5FStWaLHwgQMHWt1X18tD4+Gqq66KuBXIe8ZOOTFBQBAINgKeI1rgnjhxoiYjFsmCaB988IG688471THHHKP72aRJE9/EEgdxPKRPgoDdCHiSaOl0t27dFKv3P//8s90YuFb+jh079KaNU089VRPuKaecol588UXX2iMVCwKCgD0IeJZof/31V9W0aVNVr149e3rusVKnTZumk1nixyXf2aBBgzzWQmmOICAIZIqAZ4mWDrEDC7Hw7t27Z9o/3523dOlS1b59+4gf9/rrr1dsjBATBAQB/yLgaaIFVnRimeXNmTPHvyhn0PL169frbBT/+te/dP/r1Kmj3nzzzQxKklMEAUHAbQQ8T7QAhFwhZLt161a38XK8fvKtjRkzRtWuXVtjcNxxx6knnnjC8XZIhYKAIJA5Ar4g2r/++ksnVaxWrVrmPQ3AmXPnzlXkN+NHh9ddd92l/vzzzwD0TLogCAQbAV8QLUPwf//3fwqi7dixY7BHJIXeER52++23q8KFC2vCbdy4sVq7dm0KZ8ohgoAg4AYCviFawCH0qUCBArKz6n9XCuFhgwcPVqiGMcOtVKmSmj17thvXkdQpCAgCSRDwFdHSD4gFUpEZXM5RJVPFxRdfrLEh31n//v1zHiDvBAFBwDUEfEe0INWuXTt14oknugaalysmPKxt27aacPlBatWqlfr222+93GRpmyAQeAR8SbRbtmxRZ599trr22msDP0CZdpDwsJ49e6rSpUtr0gUvSFhMEBAEnEfAl0QLTK+++qoqWrSoGj58uPOo+ahGwsNGjx6tatWqpQkXGUrCxfxs7KJDdCj2RbYOMUHAiwj4lmgB8/HHH9fkgeKXWO4IsJh4xRVXRNwKRC7s378/9xM9dsSZZ56pypcvryU1L7rooshfIVqPDZQ0J4KAr4mWXnTq1EknSSTWViw1BN5//30tsn7UUUdp0m3UqJFas2ZNaie7fNSePXt0myU3m8sDIdWnhYDviZYQpwsuuEBBFmLpIbB9+3b10EMP6bAwFs7QlZg5c2Z6hTh89FtvvaWJVmavDgMv1WWFgO+Jlt6jAYAmQN++fbMCI8wnP/300+rCCy+MuBXY9uxFGzBggPbNe7Ft0iZBIBECgSBaOjdhwgRNEgsXLkzUV/k8BQSWLFmiUAxjhsurZcuWykuzRzJUVKhQ4R8LYSl0TQ4RBFxDIDBEC4J33323Jocff/zRNUCDUvG6detUjx49VKlSpTSmiNosXrzY9e6xCBa7EEZKIDFBwMsIBIpoycZw6aWX6kSIXgbdT23bu3evGjlypKpZs6Ym3OLFi+toDzf6wMyaWTZ+WjFBwE8IBIpoAZ4VdRZ1ULYSsxaBF154QV1++eWa7CA8Ij7IhOGUEWlAvUQeiAkCfkIgcEQL+M8884y+IWfMmOGnsfBNW9977z1NsgULFtQ4N2zYUKEoZrexEIbbQEwQ8BsCgSRaBqF3796aBNiuK2YPAtu2bdOLUjxBMNOsWLGi/pGzpzalNybcdNNNdhUv5QoCtiEQWKL9448/FCvUp512mm3gScF/IzB58mR1/vnna8KFdHv16vX3lxb9x5ZrIg5QKYt+WVS8FCMI2IZAYIkWxJBSRCz8xhtvtA1AKTgnAoSHtW7dOkK41113ndq8eXPOgzJ4h18W10HsC90DMUHA6wgEmmgB//nnn9di4ZJny9lLkfCwe++9V5UsWVKT7llnnaUkxtnZMZDavINA4IkWqNlmyuOsX/bze+fyyL4lhIch/lOjRg09Bjz+Dxs2LPuCpQRBwEcIhIJoGQ92O7FNV8w9BAgPa9asWcStcOutt6qffvpJN+i7777TBMzmAxGMcW+MpGZ7EAgN0W7atEmLhbNAFlb7+OOP1UsvvaT1aZcvX+4aDISHQbL58+fXpFu/fv2IQDlPHrzuv/9+19onFQsCViMQGqIFOHyEPLoOGTLEahw9XR4LSR06dNAEZvRbwYGVezeD/wkPI7dZsWLFIrNcQ7T8/eWXXzyNqzROEEgVgVARLaCQkYGbGMWvsBhkyiN5tDgMs1vIdtSoUa7DcNlll8UlWlLMiwkCQUAgdETLoHXs2FEhek2sbZjNzG7dwoDU6LgNomexsf+TF27Dhg1uNVHqFQQsQSCURMsjK2LhPDqH2SBap3da/fDDD3o3mQn7ImMvsbfEOhuSxXd77rnnqm7duilynPE5ojbz588P83BJ332MQCiJlvF64403dBQCW3XDaE4rYb3zzjsRnVtSxSPSvnHjxhzQ837lypX680KFCmnVMERrHnvsMXXGGWdowj322GPVI488kuM8eSMIeB2B0BItAzN+/Hh984ZxpkSCQyciMKZOnarYrMCslC26bNU9ePBgrvcFoWCcs2zZssixbD5p0qSJ/pzvbrnlFkVYmJgg4HUEQk20DA5yity0u3fv9vpYWdY+3AUQrV0RB99++60W9WGxDWxvuOEG/QSRbgcI8apUqZLC3RBt7777rvaz58uXT5ffoEEDJZmQoxGS/72GQOiJloB5xMJr1arltbGxpT12kizumKuvvlqTX7ly5XToVrbqaYxNixYt4mIBoffr109LJ0LoSChOnDgx7rHyoSDgJgKhJ1rAx3+IxN/tt9/u5ljYXrddJIuOBOI9kB0LjAi9HD582JL+7Ny5Ux133HF6G3WyAp966ilVt25d3Qbacd9996lDhw4lO0W+EwQcQ0CI9n9QT5kyRd+kQVWDsppkWbgiR1vhwoU1bjfffLOya7fZq6++qutgV1tu9tprrykUwyBbXsyGP/vss9xOk+8FAVsREKKNgrdnz5765oxdDY86xJf/sikB0iFEKlrH1fzP5oVUbdGiRapp06a6PLRhBw0apLZu3Zrq6RkfN3jwYHX88cerr7/+OqUyIFc2aZhdZ/ikWWATEwTcQECINgr1AwcO6JV4MgYEyUhmGKvjGv0+esdYvH6zsYMQq1NPPVUTLKlr3EgTdM0116jGjRvHa2LCz0x4mHFtFClSRD388MMJj5cvBAE7EBCijUGV2d3pp5+uYz5jvgrd208//VTddtttEfEXkjH+5z//cQ2Hffv26QUvnjwyMcLDWFwzbgV2CO7YsSOTouQcQSAtBIRo48DF1tACBQpolas4Xwf+oxdffFExa4WQCK9ChGf79u2e6Dd+YNo1c+bMjNtDeBg+5bx58+qycKFEx+tmXLCcKAgkQECINgEwPFpzQ69atSrBEcH6+Oeff9aP1ERf0G9mfvzgeNFGjhypF+GyFZ0x4WEnnXSS7jMhaZKJw4sj7v82CdEmGcM2bdro0KIkh/j+K9KEE5EAuTLDI8Tt/fff93y/2rdvr8O5/vrrL0vaSnjYeeedp3EAix49eoRedMgSYKUQjYAQbZILAdWo2rVrK2T8gmbPPvusFtaBVCpXrqzlI/22Ow5futWxz4SHERIGLrzYgPHJJ58EbfilPw4jIESbC+DEbrKVlLxjfjeC/xFzQdQFEiFMy88hTx9++KHux5NPPmn50BAeRpyw2UZMzrPnnnvO8nqkwHAgIESbwjgPHTpU39BLly5N4WjvHcICEnKEkCsShF26dFGQVBBs0qRJul8scNlhZHkYMWKEjkQBv2OOOUYR0ysmCKSDgBBtimixSo2IyW+//ZbiGe4fBgkZv+Npp52ms9HGCrS438rsW9C5c2dVvXp1xYKenTZnzhzVqFEjTeyQLtfEN998Y2eVUnZAEBCiTXEguaGQ+SMjgJftyy+/VL169YokO8S/HAYZyDp16qh27do5MjRoY7CAmCdPHk26CKgjXi4mCCRCQIg2ETJxPsd1QMrye++9N8637n7EIk7Lli31jV+wYEHVtWtXlc7WWndbn33t69evV0ceeaR+zM++tNRK4Mf3wQcfVGXLltW4EyaGxrGYIBCLgBBtLCK5vB8zZoy+qQjqd9sIbRo3bpyOjOBRllX40aNH2/4I7Xa/E9XPJgZwcMOXjpvmnHPO0fXThu7du/vKzZQIU/ncGgSEaDPA8c4779Q3lFvbNz///HN9I5t8Ws2bN9ep1DPoSuBO4WkDsRvywrlhixcvVmgyQLa8yGKxevVqN5oidXoIASHaDAbj+++/1zunWIBx0hYsWBAR1iaLL+pU2e6OcrL9TtXFllon0vQk6w/jgvsGERsIl5xn2WwbTlaXfOd9BIRoMxyjt99+W4uFk7fKTtu7d69OUkgcJzcs5D527FiFwIpYfASYzZLEsX///vEPcPBTIiGGDx+uqlSposfv6KOP1tKSDjZBqvIAAkK0WQwCiQYhP/5abTxuks/MzIiYoSGALZYaAsz+GZt58+aldoIDR6EdYcR6aFuHDh0UUSJiwUdAiDbLMWZPPDfNunXrsizpv6ezU+vyyy/XZRIcj8+RFXWx9BEgnxhpcLyGH1KTN954ox5jrp0LL7xQfkTTH15fnSFEm8twIYo9cODAHK/osCk2MDDbJLQnUyNlNrvPqlatqm8+3ASECf3++++ZFinn/Q8BfrQuueQST+JhwsPKlCmjx52t0USRiAUPASHaXMaUHGLMOghK50VKFN4jNmLSda9Zs0aHVpGrKh1j2yi7mgoVKqTLZLWaeFgx6xAgw8IJJ5zgydjn6F4SHsamC64tXt26dVNs/xULBgJCtLmMIyv7kGu0Gf8f3xljRRmxcFK+5GazZs3SKVm4oVi0IWNr0PKU5YaBk9+//vrrmrymT5/uZLUZ1UV4mEnZzvVx5ZVX+kK2MqPOhugkIdpcBptZLNstY43PSPwXbewS4uZ49NFHVZ8+fRSpU4whMo0YySmnnKKPqVWrlkJ16uDBg+YQ+WsjArhm2DHnFzEdEx6Gn55rimgTN/K02TgkoSpaiDaX4eYiJ4tsrBmXQrS/9vDhwzpYnnPMC30EclOxPZTPrr32WtkXHwumQ+9btWqld28RMucXM+FhJjEm6d2DINnpF/ytaqcQbRIkIVHIMZpMzeFklo39Dp+rIdjov8ROIvSyefNmc7r8dQkBnihIMulHIzysQYMGkWuMpypxOfljJIVok4wTM1kIM57F+87McqNJlv8ff/zxeEXIZy4gQJoexsTP4i+x4WEXXHCBeuWVV1xAU6pMFYH4LJLq2QE/jhkDPtp4xnfly5fP8RWq/LEky/vixYtrlSfRLs0Bl2tvCKFiXHgq8bNt3bpVZ8xAUY7+ECaG6JGY9xAQok0yJkQbREcWmEOJrWUhLN53JntuNOEOGzZM1axZU98MEDR6pmLuIoBoN3HLbgkDWdl71gYmTpwYUXHj2uPa/PHHH62sRsrKAgEh2iTgccESyhVtxM4iWkIuKRNHG/09/+OLRUaRsCIWw5DPw/jM7PrC1+bVdN6x/Qnqe35IyXQcJGObNhtozA89ym64GsTcRUCINgH+ZrGL2asxSJeZKSQbb4HMHBf9lw0IPNqh5GSMRbPbbrtN5+9icQbREbvTsJi65e/fCCA3CSER+hU0+/TTT7VWBlEK9LFatWqKzMdi7iAgRJsAd+MCYPZqHvu5YHn0jybfBKfn+NgsnMXOYPHZEqpTsWJFHeMJGYvsYQ7obH8zdepUTUSLFi2yvS43KuCpC9cVKeW5fpHXZEu5mLMICNEmwBsyZVYb/UrkKkhQRI6PjVh4ogWxp59+WrsZuBnYGcQOITFnEEAlDa2KoIdKkS6diQPXGC+EbbwmuOPMiDtfixCtQ5jv3r1bb7slG20yw9XQunVrfSPUrl1bsQeelDVi9iJQr149dcUVV9hbiUdKR0v5hhtuiBAuCUcXLlzokdYFsxlCtA6O64oVK7SbgJlEboYLAYlE0tWUKlVKh/EQziNmDwJskUbcp2/fvvZU4MFSv/76a71VvHTp0pp0Ed8h55yY9QgI0VqPadISmaHy2EY4TirGIhkbHkiFYh73ZBU5FeTSP4aoEDCO9aWnX5K/zjh06JDW3UB/g/7zuvvuuxVPYWLWICBEaw2OaZVixMLTXfiaM2eOatq0qb4RJDwsLchTPrh37946Rvqjjz5K+ZwgHRgbHoY7BVeDWHYICNFmh19GZ6ORivwdYV+ZGDNacpUhVGPCw3766adMipJz4iDQuHFjvSNw//79cb5N/hGLp8uXL9evbBZPk9di/7cmPIwoBWa4pLL3g8yk/chkVoMQbWa4ZX3WqlWr9MWbTbZWfGwkICxXrpyEh2U9In8XgLuGFDjxdv79fVTO/wgHZLcgMdZs2+Yv72M3vOQ8y/vvTHhYpUqVNOHix6avskCb3tgJ0aaHl6VHE0COWLgVAfP4fuvWratvBknkmP0wLVmyRGP51FNPpVQY5MNsNtqIuY7VLI7+3m//x4aHEbmQrvvLb322qr1CtFYhmWE5RizcKj8YPjZS6vC4d9ZZZ+lFtz///DPD1oX7tEGDBql8+fKplStXZgQExMs4pLqLMKNKXDgpNjyM0LiXX37ZhZb4p0ohWpfHikcw4mbZKok4iFW2du1a/ejLI6wJD0t3R5tVbfFzOWweIZ45kxV4I5vpZ19tsrEz4WFcX/ygsOYQTyQ/WRlh+U6I1gMjjbwiNzORBFYbCf7QUmAxg5uBGF4JD0sdZUKf8IGTJSNV4wftmWee0W4DXApBt3jhYWwn3759e+C6numPphCtRy6FuXPn6gWU+++/37YW4WNjRR3ClfCw1GE2mTNGjhyZ9CTjKgBfXmHUFECAnIgagwFqdZm6XpKC7eCXjGv01mX6VqFChbQ0T4RoHRyw3Kp65JFH9AVqt8AJO9Q6dOig62I1GdGR77//Prfmhfp7IwyUTIOC2Q43JS/cBsgwIkiU6SzIz4DjuurSpYuOhoGY0P5llu83M+4fFjYZV/zt/E33SUWI1mMjjyA1F6YTcbFGob9s2bI6+gFxlU8++cRjiHinOe3atVMkSdyyZUtKjYJgGcsw+y25jomqOfnkkzUWZCImJPH3339PCUM3D4JQGT/INlsTos0WQYvP5yZGLJyIASeN1OcIlHNhSXhYYuSZmbVs2TLxATHfkO4o3dlPTBGBeTtr1iwdY8w1xosfLjZGeNUYu0SprNJtsxBtuog5cDwhWqzg3nHHHQ7UlrMKVJyuueYafSOY8LADBw7kPCjE74gbhSQI/crNeMzkWL9vWsitn+l+j8+2ffv2GhvwIf77pZdeSrcYW49nzGibVaF5QrS2DlfmhbPwwkDPnDkz80KyONNswTzmmGMi4WGSLv2/gKIdzNi88MIL+gMeMfHFsvgFYfDq1q2bjjqwakaUxVB69lSiMx544AFVsmRJjScqYrktODrVGXYFxiZfzaZuIdps0LP5XCMW7mb8K7oM+NjQ0YVc2A3EYlrYjVREZJ1l0QdfLH5YSDX6ZYVvLww4E0s+YcKEHJlMWC9AutItM+NoVf1CtFYhaUM5O3fu1OFYRAZ4wWbMmKEuueQSTbiEuxAuFmY7++yzVbNmzXyxsOOXcSLihoSS/Kjzuuyyy1z5YRei9csVY1E733zzTS0W3rZtW4tKzL4YfGxGod+Eh2Wycyr7lrhbAlEbefPmVb169XK3IQGsnegXnujy58+vCbdKlSqWrP6nChULwpCtVSYzWquQtLEcIgL4dR8/fryNtaRfNPnP8LGxcIc4Do97a9asSb8gH5+Bn5axmTJlio974d2m//jjj+rRRx/Vkw1w5jpDH2Tfvn22NtrETeN/t8KEaK1A0YEyjFi4VaugVjeZHwG2EXMzMBsIUw4qUg4VKVJEvfPOO1bDKuVFIRAbHsZTHj5yu4zFMNTX2GhhNIZJ9ZPJmokQrV2jZHG5aKSytZEVWi8bPjazBZPUKMzGf/vtNy832ZK28ZhJ/PMPP/xgSXlSSGIEYsPDzjvvPFtC6FjkZEcYwkxMIHix20+INvHYBOKb999/X4vDsH/c60a8KT42FPr5cejTp0+g03mzA4pZLX0WcwYBEx6GSDskePzxx+v8es7Unl4tMqNNDy/XjxcpMQkAABD3SURBVOYxhgUCdBH8YISH0VZS7nAzsIhmld/La/0nVTx9HDNmjNeaFuj2xAsPQ2eBNQSvmBCtV0YijXYYsXC/ERbhYTxiQ0aEh7m1GSMNqNM+lE0LefLkUWRoEHMegdjwMMLv8K+6bUK0bo9ABvX/8ccfWiycma0fsyeg0M9CBoRLeBgbInbs2JEBEt48hdhPdoohjC3mDgImPIwMGVxnbLiZOnWqbsyIESNUjRo1tKKYU1KWQrTuXAdZ18pqK6v8LMD41dj5QwwqCv0mPOzDDz/0a3ci7eZRlpA3RNbF3EUgNjyMuGeIN/rF+oHdJkRrN8I2lv/888+rY489VvXs2dPGWpwpety4cZEtmEQteE1kJF0UyGLBzewXX3q6/fPj8biqWLCMJln+P+mkk2zvjhCt7RDbW4ERC/c7MRmU8LERVcENQHjYE088oVhQ86M9/vjjuh/z5s3zY/MD1+bp06ero48++h9Ei2aF3SZEazfCDpRvsiUEKUsC4WGdO3fWLgUTHrZ+/XoH0LS2ilatWmk/NHnhxJxHAPdUv379FMpg/Hjjooqd0d533322N0yI1naI7a9g06ZN2ld7xhln2F+ZwzXs3btXPfzww5EtmISHvfHGGw63IrvqWPBD4/fgwYPZFSRnp4wAETnXX399hFQRAMLVhrEAVrFiRXXiiSc65nYTok156Lx9II/c/Gp36tTJ2w3NonX42Fj8Y0ZCeBiPgn4wtH1pM7oQYvYigFawyRQC5giMeyGLgxCtvePuaOlGLNyPSfDSAYqFpjZt2mjyIhfVkCFD1LZt29IpwvFjn3rqKd3eoI+N48Aqpb788ktF9ugSJUpojNEnYO3CS6GPQrRuXBk21kn6G37JcSf41XjsS2U/OeSKf40bjJhidgOxTdmrdsstt+inDi+30avYxWvX0qVL1XXXXaevd655NA/mz58f71DXPxOidX0IrG0A5NO4cWNVrlw5awt2qDQjT5duQkPUw/BRc8MRHubVlX4C5RmfMKYgt+oSQqiIiBTGmheZo9etW2dV8baUI0RrC6zuFspiEc5+Vrz9ZEhA8tiXTebYV155RWc94AbkZhw7dqxC+cwrxkydtnXt2tUrTfJFO7744guFVKiJg0VAZtiwYb5oO40UovXNUKXXUCMW7ieBEyTomMmih5DujDYWHcKpWBg88sgjtXpY79691eeffx57mCvv58yZo8nWa0LuroCRS6VkhEbf2MxeL7jgAl9qHQvR5jLQfv4aQWou0NWrV3u+GxArRItZQbSmwyjxszCCKwUsWIXGt+e2de/eXRUuXNh3oWpO4Hbo0CH9JFK9evUIwfKj6ed1ByFaJ64cl+pAIxV/JcLFXjYWv2ijWQCzkmij+41Cf7169fTNSx2IjKBL4JbVrVtX8XIz26tbfY9XL08hd999typUqJAeI+JcvZJ+PF570/lMiDYdtHx47LvvvqvFwi+99FJPtp5FoQoVKuh03aaBdhGtKZ+UMy1bttQ3M+FhgwcPViRadNrIxlCwYEG9mON03V6qj+3jKJ4Z90CDBg3U4sWLvdTErNsiRJs1hN4vwIiFP/TQQ55rLKlC8MFFm91Ea+ravn273hnEbJrwsNtvv13xw+Sk4YOEYJCKDJMh9YkWBPKF9B/8yU5hnmqChoUQbdBGNEF/jFi4l7avLliwQN9kzGhM8jv+ouWKfgP/OxUGhXhNtWrVdHuaN2+uXnzxxQRIWv9x//79db3gEXRDJ5ZYbxYpIVi2JxMZEnQTog36CP+vfwcOHNBi4Vzc/O8FYwGM9iR7OZ1FghkmbhbaBOGT9RRNU7utSZMmOg7Yj8I5qWDDDxfxw2as+f/1119P5dRAHCNEG4hhTK0TxKkiFn7uueemdoJLRznlOkjWPULBWOmGGEj+h+avnXvm2S7KDjd2Oh0+fDhZ03zz3f79+9Wjjz4aEQRCopDFrjAu/gnR+uaytaahRiyc8CKvmheI1mBDqnTCw1gBh3RRhCIJox1Gih/qwM3jZyOc8NZbb43MXqtWrarTzvu5T9m2XYg2WwR9eL4RC587d64nW3/PPfeoadOmea5thIfxNAAZXnjhhQqlKKuFS8hnRfkksvSbPffcc1pVjfbzIpLAadePVzETovXqyNjcLiMWvnPnTptrCl7xhIexvRkyITyMaA4UpKwy3AeEvPkhfxrZLwYNGhSZ8RcvXlyxUWbXrl1WwRGIcoRoAzGM6Xdiw4YNWtu1SpUq6Z8sZ2gECA8juST778m2ettttyke/60w8lg1bdrUs2l8UCAjNM/MXlk4nDx5shVdD2QZQrSBHNbUOrVw4UIt29exY8fUTpCjEiIwYcIExY8WxEPOM/QMsjHCoCirW7du2RRj+bmIrdevXz9CsOw8RB9YLDkCQrTJ8Qn8t0YsfMqUKYHvqxMdZEdTdHgYQfmZ5nKbNGmSJjQEgtw0tnJH590ilToiPexsE0sNASHa1HAK9FFGLBx3gpg1CKCPiiuBWSnhYfgtmaWma2itkpzSjUUlZqpt27aNzF5JEePFRcp0MXXjeCFaN1D3WJ3ffPONDiY/4YQTPNYy/zeHWFJS7YAtpNu6dWvFpoh07PTTT9f+9B07dqRzWsbHxubdYnFOskJkDKc+UYg2O/wCcza7dFjpbtGiRWD65LWOEP5kwsNIMolrIJVdelu2bNEkTSocu+y7777LkXcLWcm+ffuqX375xa4qQ1WuEG2ohjt5Z41YOH5FMfsQQLiGmS0zXDJhoHWwefPmpBVC0hxPnK2VtmLFioiSGeXzA0C2YTFrERCitRZP35dmxMLlUdH+ocQVwKISAuCEhzFjhfgSGRs5kFUkWiRbi867RZnt2rXzhUB8tv1263whWreQ92i9rJATssPNL+YcAhCfkQwkfpYZbDwj0ysxqxs3boz3ddLP2JwSnXercuXKauDAgYptxmL2IiBEay++viyd1Wb2pzds2NCX7fdzo9FRQMmLx3iy+uIqiN5lxQ9hnjx5tOsh1X4uW7ZMXX311bpMymVcs43zTbVuOe6/CAjRypUQFwEjFo7/UMx5BJBL7Ny5syZHVL3YuLBmzRrdkEWLFunPc0tgOW7cOGXybrF7jVCxtWvXOt8ZqVGy4Mo1kBgBVp2ZAf373/9OfJB8YysCRCUgNcgmAcaCUCt8tEbIvU6dOjqpJb51QsmQIIzOu4WY+cMPP6zIaCDmHgIyo3UPe8/XjO/OrI7v3bvX8+0NegNnz56t8NFCuGQM5m/0q1SpUpH3zZo1U/PmzQs6JL7pnxCtb4bKnYbyuHrWWWdpwXB3WiC1xiLw3nvvRdLuRBMt/6Mqhmi5mLcQEKL11nh4sjVGLJxHUjH3ESCBIZEHsSTLe+PHdb+V0oJoBIRoo9GQ/xMigJ+PGxnSFXMHgeh8ZvFItkaNGu40TGrNFQEh2lwhkgNAgDxWRix827ZtAoqDCDz22GNaYBxyLVOmjF7sIo524sSJ6pRTTtE/gCiG2ZnTzMHuBrIqIdpADqs9nUKRii2a3Nxi9iKwadOmHHm3WARLtDXa6nQ69vYsnKUL0YZz3DPutRELv/HGGzMuQ05MjAD4NmjQQM9S8+bNqxe30LgV8zcCQrT+Hj9XWs/MisdY1KfErEFg6NChivQ14IqK2n333WdpHjJrWimlZIqAEG2myIX8PCMW/tlnn4Ucicy7j9B6dN4tMuuOHTs28wKTnHnVVVdpEo9dRFuwYEGSs+QrqxAQorUKyZCV8/XXX2uxcILkxdJDYP78+drXDekVKlRItW/fXi1dujS9QtI8unz58prUydQQ/dqzZ0+aJcnhmSAgRJsJanKORsCIhTNbEkuOAFEbhMiZrbQodbHFmS2zdhtkCqnL7NVupBOXL0SbGBv5JgUEjFj48OHDUzg6fIfgWonOu9W4cWPHfdvMYCFamb26d/0J0bqHfWBqNmLh77zzTmD6lG1HXnjhBUUyQwiuaNGiWtT7zTffzLbYjM5H5QvXgZh7CAjRuod9YGrevXu3FgsvUKBAYPqUSUeIZ0VIm6y3ECx6sg899JBCcNtNu+iii/SW3eXLl6vol5ttClvdQrRhG3Gb+mvEwrmpw2akEUfMBXLldfnll3sqLTczatM28zeM4+TmdSlE6yb6AavbiIX36dMnYD2L3x3SzdSqVUuTGNEXhLy9/fbb8Q926VMEaCBX/LRi7iEgROse9oGs2YiFI4ASRENcu1+/furYY4/VBFa7dm0tzE2KGS8akQYQrSyEuTs6QrTu4h+42hEIN2LhP//8c2D6t3r1anXttddq0oK4WrRooWbNmuX5/pE5F5FwMXcREKJ1F/9A1m7EwoNwg8+YMSOSd+vEE0/UubsQ3vaL4Ytl95mYuwgI0bqLf2BrN2Lhd955p+/6+Ouvv6oHHnhAHXXUUXoGW69ePTVy5Ejlxxk6s+9Ro0b5bgyC1mAh2qCNqIf6Y8TC/fCIDWwffPCBMpoA+fLlU23atFFz5871EKLSFL8iIETr15HzQbv/+uuviFg42ghetWnTpim2xDL7O/nkk1WvXr0UPlkxQcAqBIRorUJSyomLAGLh9evX19J/cQ9w6UNW4Xv27KmYuUKwF198sRo/frzat2+fSy2SaoOMgBBtkEfXI30zYuHt2rVzvUVsE2ZDAeRauHBhhYA57RMTBOxEQIjWTnSl7AgCRix8woQJkc+c/Gfy5MmRvFtVq1ZVDz74oGJHl5gg4AQCQrROoCx1aASMWPjatWsdQYRNBN27d9ezV2awTZo0URDuH3/84Uj9UokgYBAQojVIyF/bEWA7aKNGjVSxYsVsrWvFihWaVCHX4sWLq06dOqklS5bYWqcULggkQ0CINhk68p3lCBixcPykVhvauOXKldMzWDZLDB48WK1fv97qaqQ8QSBtBIRo04ZMTsgWAfy0zDaHDBmSbVFagrBr164R90Dz5s3V9OnT1aFDh7IuWwoQBKxCQIjWKiSlnIQIEEpF+BTxqsaMWDiP+ZnYsmXLtBsCwi5durTq0qWLKFRlAqSc4wgCQrSOwBzuShA2gRCjc4vt2rVLMfvMkyePYmNDqkasa5kyZXR5derUUcOGDVNbtmxJ9XQ5ThBwBQEhWldgD0+lRg8Vko0VmzZi4eeff35SQEhgiGYCZM0LFa3Zs2cnPUe+FAS8hIAQrZdGI4BtQTkKgkXYJF60Ae6E/Pnzq7p16+rjINSNGzdqJEjBjcsBcmWRC3eD5CUL4EUSgi4J0YZgkN3qosm+yl/zf7y2kDjQzFb5S+oVMhbwP7Pd0aNHq23btsU7VT4TBHyBgBCtL4bJn42M1kI1RPvxxx/n6Awz1GiSNf/jf50/f36OY+WNIOBXBIRo/TpyHm+3IVZ8tMYgUT6PtsWLF8clWitCv6Lrkf8FATcREKJ1E/0A1x3rDjAz1VgR6gMHDqgSJUr8g2xXrVoVYHSka2FDQIg2bCPuQH9Z4MLPSmJAZrDmxW6tAQMG/KMFzGqrV6+uyZbQLbeEZ/7RMPlAELAIASFai4CUYv6LAJsTKlSoEJdQ8dlGx9LGYrZz587Yj+S9IBAIBIRoAzGM3ukEM1Zms/HSW/NdbCytd1ouLREE7ENAiNY+bENXMuRKrGw89wBg8Hm8WNrQASUdDh0CQrShG3L7OgzR4o+NN5ulViIQYqMO7GuNlCwIeAcBIVrvjIW0RBAQBAKKgBBtQAdWuiUICALeQUCI1jtjIS0RBASBgCIgRBvQgZVuCQKCgHcQEKL1zlhISwQBQSCgCAjRBnRgpVuCgCDgHQSEaL0zFtISQUAQCCgC/w8Yk5/Rr9Pe0wAAAABJRU5ErkJggg==[/img]