Lerne GeoGebra CAS Rechner
Willkommen beim [url=https://www.geogebra.org/cas]GeoGebra CAS Rechner[/url]! Lerne in dieser Anleitung, wie du Gleichungen löst, Ausdrücke faktorisierst und erweiterst, Integrale und Ableitungen findest und vieles mehr.
Table of Contents
- Erste Schritte
- Vergleich der GeoGebra Mathe Apps
- Einleitung
- Erforsche die App
- Grundlagen
- Funktionen definieren
- Terme und Variablen
- Gleichungen und Ungleichungen lösen
- Gleichungssysteme lösen
- Grenzwerte von Funktionen
- Ableitungen bestimmen
- Bestimmtes und unbestimmtes Integral
- Vertiefung
- Rationale Funktion
- Rotationsvolumen
- Kurvendiskussion
- Polynom vierten Grades
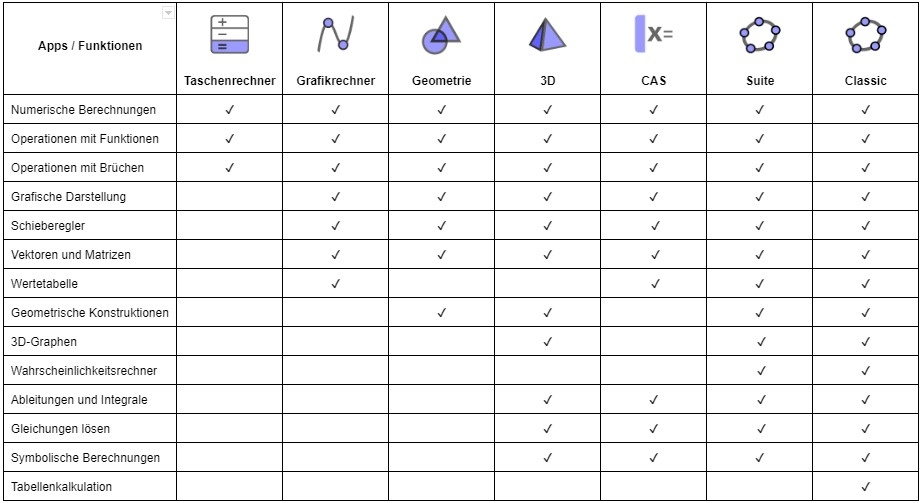
Vergleich der GeoGebra Mathe Apps
Mit unseren [i]GeoGebra Mathe Apps[/i] kannst du Funktionen, Geometrie, Algebra, Statistik und 3D auf eine neue und interaktive Weise erkunden und lernen.[br][list][*][url=http://www.geogebra.org/scientific]Taschenrechner[/url][br][/*][*][url=https://www.geogebra.org/graphing]Grafikrechner[/url][br][/*][*][url=https://www.geogebra.org/geometry]Geometrie[/url][br][/*][*][url=https://www.geogebra.org/calculator]Rechner Suite[/url][/*][*][url=https://www.geogebra.org/cas]CAS Rechner[/url][br][/*][*][url=https://www.geogebra.org/3d]3D Rechner[/url][/*][*][url=https://www.geogebra.org/classic]GeoGebra Classic[/url][br][/*][/list]Die richtige App für dich ist die, die deinen eigenen Bedürfnissen entspricht und, wenn sie in Prüfungen verwendet wird, die Prüfungsbestimmungen für deine Region erfüllt. Die folgende Tabelle gibt einen Überblick darüber, welche Funktionen in welchen Apps verfügbar sind.
GeoGebra in Prüfungen
Wir glauben, dass die Schüler*innen davon profitieren, wenn sie im Unterricht, bei den Hausübungen und während Prüfungen genau dieselbe [i]GeoGebra [/i]App verwenden. Auf diese Weise erhalten sie die meiste Übung mit der App und können unsere Technologie daher in allen Situationen optimal nutzen. Aus diesem Grund haben wir unseren [i]GeoGebra Prüfungsmodus[/i] erstellt und ihn in jede unserer Apps eingefügt. Der [i]Prüfungsmodus [/i]sperrt mobile Geräte, sodass die Schüler*innen während einer Prüfung keine anderen Apps als [i]GeoGebra[/i] verwenden und mit diesen kommunizieren können. Dieser Ansatz wurde bereits von mehreren Bildungsministerien in mehreren Regionen erprobt und genehmigt. Erfahre mehr über die Verwendung von [url=https://www.geogebra.org/m/m97r7cd4][i]GeoGebra[/i] in Prüfungen[/url].[br][br]
Funktionen definieren
Aufgabe
Definiere eine Funktion, zeichne deren Graph in der [i]Grafik-Ansicht[/i] und bestimme einige Funktionswerte und Argumente.
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1.[/td][td]Gib die Funktion [math]f\left(x\right)=x^3+6x^2+6x-4[/math] in die [i]Eingabezeile[/i] ein und drücke [i]Enter[/i], um eine neue Funktion zu definieren.[/td][/tr][tr][td][/td][td][b]Anmerkung:[/b] Der Graph von [i]f(x) [/i]wird automatisch in der [i]Grafik-Ansicht[/i] angezeigt.[i] [/i][/td][/tr][tr][td]2.[/td][td]Berechne die Nullstellen von [i]f(x)[/i], indem du [math]Löse\left(f=0\right)[/math] in die [i]Eingabezeile[/i] eingibst und [i]Enter [/i]drückst.. [br][/td][/tr][tr][td]3.[/td][td]Bestimme die Funktionswerte für [i]x = -5[/i], [i]x = 0 u[/i]nd [i]x = 2.15[/i], indem du [math]f\left(\left\{-5,0,2.15\right\}\right)[/math] in die [i]Eingabezeile [/i]eingibst und [i]Enter [/i]drückst.[/td][/tr][tr][td]4.[/td][td]Ermittle für welche Argumente [i]x[/i] [i]f(x) = 4 [/i]ist, indem du [math]Löse\left(f=4\right)[/math] in die [i]Eingabezeile [/i]eingibst.[/td][/tr][/table][b]Anmerkung:[/b] Du kannst zwischen [img]https://wiki.geogebra.org/uploads/thumb/6/66/Numeric_toggle_button.png/24px-Numeric_toggle_button.png[/img] numerischer und [img]https://wiki.geogebra.org/uploads/thumb/8/8b/Symbolic_toggle_button.png/24px-Symbolic_toggle_button.png[/img] symbolischer Ausgabe umschalten, nachdem die Funktionswerte und Argumente berechnet hast, indem du den entsprechenden Umschaltbutton auswählst.
Versuche es selbst...
Aufgabe
Zeichne eine Familie von Funktionen und vergleiche deren Funktionswerte mit Hilfe der [i]Tabellen-Ansicht.[/i]
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1.[/td][td]Gib die Funktion [math]f(a,x)=\sqrt{x-a}[/math] in die [i]Eingabezeile[/i] ein, um eine Familie von Funktionen, abhängig vom Parameter [i]a,[/i] zu definieren.[/td][/tr][tr][td]2.[/td][td]Gib die Funktion [math]f\left(0,x\right)[/math] in die [i]Eingabezeile [/i]ein und drücke [i]Enter.[/i][/td][/tr][tr][td][/td][td][b]Anmerkung:[/b] Der Graph von [math]f\left(0,x\right)[/math] wird automatisch in der [i]Grafik-Ansicht [/i]angezeigt.[/td][/tr][tr][td]3.[/td][td]Wiederhole Schritt 2, indem du [math]f\left(1,x\right)[/math], [math]f(2,x)[/math] und [math]f(-1,x)[/math] eingibst, und zeige deren Graphen in der [i]Grafik-Ansicht [/i]an[i].[/i][/td][/tr][tr][td]4.[/td][td]Vergleiche die Graphen der Familie von Funktionen und beschreibe, wie sie sich unterscheiden.[/td][/tr][tr][td]5.[/td][td]Aktiviere den [i]Mehr[/i]-Button auf der rechten Seite von [math]f\left(0,x\right)[/math] und wähle [i]Wertetabelle [/i]aus.[/td][/tr][tr][td]6.[/td][td]Lege im Dialogfenster den Startwert mit -1, den Endwert mit 5 und die Schrittweite mit 1 fest. Wähle [i]OK[/i], um deine Einstellungen zu bestätigen.[/td][/tr][tr][td]7.[/td][td]Wiederhole Schritt 5 für [math]f(1,x)[/math], um ebenfalls eine [i]Wertetabelle[/i] für diese Funktion zu erstellen. [br][b]Anmerkung: [/b][i]f(0, x) u[/i]nd [i]f(1, x)[/i] werden automatisch mit [i]g(x)[/i] und [i]h(x) [/i]bezeichnet.[/td][/tr][tr][td]8.[/td][td]Vergleiche die Funktionswerte von [math]f(0,x)[/math] und [math]f(1,x)[/math] in der [i]Tabellen-Ansicht[/i].[/td][/tr][/table][table][tr][td][br][/td][/tr][/table]
Versuche es selbst...
Rationale Funktion
Aufgabe
Gegeben ist die Funktion [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math].[br][list=1][*]Zeichne den Graphen von [i]f(x)[/i].[/*][*]Ermittle die Nullstellen sowie den maximalen Definitionsbereich [i]D [/i]von [i]f(x)[/i].[/*][*]Bestimme das Verhalten von [i]f(x) [/i]an den Rändern von [i]D[/i]. [/*][/list]
Erforsche die Konstruktion...
Anleitungen
[table][tr][td]1.[/td][td]Definiere die Funktion [i]f(x)[/i], indem du [math]f\left(x\right)=\frac{x^3+3x^2}{x^2+6x+9}[/math] in die [i]Eingabezeile [/i]eingibst und [i]Enter [/i]drückst. [/td][/tr][tr][td][/td][td][b]Anmerkung:[/b] Der [i]GeoGebra CAS Rechner[/i] vereinfacht automatisch die Funktionsgleichung von [i]f(x) [/i]und zeichnet den Graphen in der [i]Grafik-Anischt[/i].[/td][/tr][tr][td]2.[/td][td]Verwende den Befehl [math]Nullstelle\left(f\right)[/math], um die Nullstellen von [i]f(x) [/i]zu bestimmen.[br][/td][/tr][tr][td][/td][td][b]Anmerkung: [/b]Du kannst ebenso den Befehl [math]Löse\left(f=0\right)[/math] verwenden, um die Nullstellen zu bestimmen.[/td][/tr][tr][td]3.[/td][td]Um den maximalen Definitionsbereich von [i]f(x)[/i] zu bestimmen, berechne die Nullstellen des Nenners von [i]f(x), [/i]indem du den Befehl [math]Nullstelle(Nenner(f))[/math] eingibst.[br][/td][/tr][tr][td][/td][td][b]Anmerkung:[/b] Du kannst ebenso den Befehl [math]Löse(Nenner(f)=0)[/math] verwenden.[/td][/tr][tr][td]4.[/td][td]Da die Lösung [i]-3[/i] ist, erhalten wir den maximalen Definitionsbereich [math]D=\mathbb{R}\backslash\left\{-3\right\}[/math].[/td][/tr][/table][table][tr][td][/td][/tr][/table]
Versuche es selbst...
Anleitungen (fortgesetzt)
[table][tr][td]5.[/td][td]Verwende den [i]Grenzwert-[/i]Befehl, um das Verhalten von [i]f(x) [/i]an den Rändern von [i]D[/i] zu untersuchen.[/td][/tr][tr][td][/td][td]Gib den Befehl [math]Grenzwert\left(f,-\infty\right)[/math] in die [i]Eingabezeile [/i]ein, um das Verhalten am linken Rand zu untersuchen.[/td][/tr][tr][td][/td][td]Gib den Befehl [math]Grenzwert\left(f,\infty\right)[/math] in die [i]Eingabezeile [/i]ein, um das Verhalten am rechten Rand zu untersuchen.[/td][/tr][tr][td]6.[/td][td]Verwende die Befehle [i]LinksseitigerGrenzwert [/i]und [i]RechtsseitigerGrenzwert[/i], um das Verhalten von [i]f(x) [/i]um -3 zu bestimmen. [/td][/tr][tr][td][/td][td]Gib den Befehl [math]LinksseitigerGrenzwert\left(f,-3\right)[/math] in die [i]Eingabezeile[/i] ein.[/td][/tr][tr][td][/td][td]Gib den Befehl [math]RechtsseitigerGrenzwert\left(f,-3\right)[/math] in die [i]Eingabezeile [/i]ein.[/td][/tr][/table]