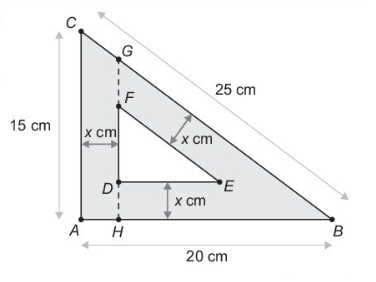
[size=100]Na figura acima podemos observar que DF=GH - GF - DH.[br]Das letras b e c anteriores temos GH=[math]\frac{3}{4}\left(20-x\right)[/math], GF=[math]\frac{5}{4}x[/math] e da figura temos DH=[math]x[/math].[br]Logo DF=GH - GF - DH=[math]\frac{3}{4}\left(20-x\right)[/math] - [math]\frac{5}{4}x[/math] -[math]x[/math]=[math]15-3x[/math].[br] Da semelhança dos triângulos ABC e DEF[br] tiramos [math]\frac{DE}{20}=\frac{DF}{15}=\frac{15-3x}{15}[/math], assim DE=[math]\frac{4}{3}\left(15-x\right)[/math]. A área de DEF portanto, equivale a A(x)=[math]\frac{DF.DE}{2}[/math]=[math]\frac{2}{3}\left(15-3x\right)\text{²}[/math]. A figura a baixo mostra o gráfico dessa função para [math]0\le x\le5[/math].[/size]