[color=#6aa84f]Analizzando i lavori di Escher e concentrandosi su quelli riguardanti costruzioni isometriche, si può osservare che in essi è sempre presente un pattern, una mattonella base che viene trasformata secondo traslazioni, rotazioni e simmetrie affinché ogni spazio vuoto venga riempito. L'artista è solito utilizzare come mattonella base da trasformare degli animali che vengono ripetuti seguendo anche isometrie relative alla loro colorazione. Analizzeremo ora nel particolare una sua famosa opera realizzata con inchiostro e acquerelli: "Fish / Duck / Lizard" (op n°69) dove sono appunto rappresentati pesci, papere e lucertole che vengono ripetuti secondo ben precise regole isometriche e più in particolare delle rotazioni attorno tre punti vertice della mattonella principale che è appunto formata dai tre animali.[/color]
[color=#6aa84f]Nell'opera, la trasformazione più presente è la rotazione[icon]/images/ggb/toolbar/mode_rotatebyangle.png[/icon] che si ha sia di un singolo animale intorno ad un suo punto estremo che coincide con quello dell'animale situato al suo fianco, sia del modulo base formato dai tre animali, sia dell'intera mattonella esagonale. Prendiamo ad esempio il pesce giallo che viene ruotato insieme alla papera azzurra attorno al punto C, loro comune estremo; abbiamo poi ruotato attorno allo stesso punto anche la lucertola rossa per completare con le due rotazioni di 120° e 240°, effettuate con gli slider[icon]/images/ggb/toolbar/mode_slider.png[/icon], la figura esagonale che è composta da tre mattonelle base e che rende una visione d'insieme più ampia delle rotazioni. Si può poi ruotare anche l'esagono attorno a uno dei suoi vertici come riprodotto dallo slider Ω. Da sottolineare che le figure ruotate attorno ai vari estremi (come ad esempio il prima nominato punto C) costituiscono in realtà anche delle simmetrie centrali[icon]/images/ggb/toolbar/mode_mirroratpoint.png[/icon] di appunto 120° e 240° in base al punto.[/color][br]
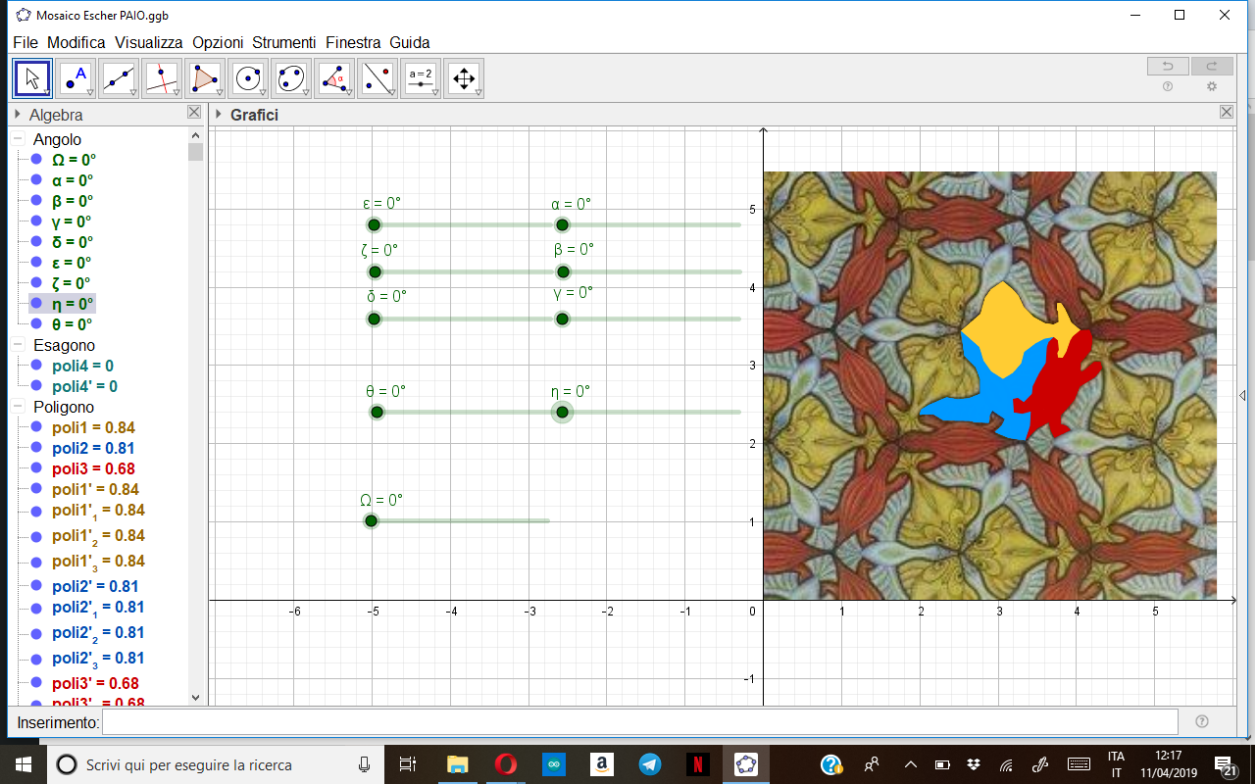
[color=#ff0000][b]Modulo base[/b][/color]
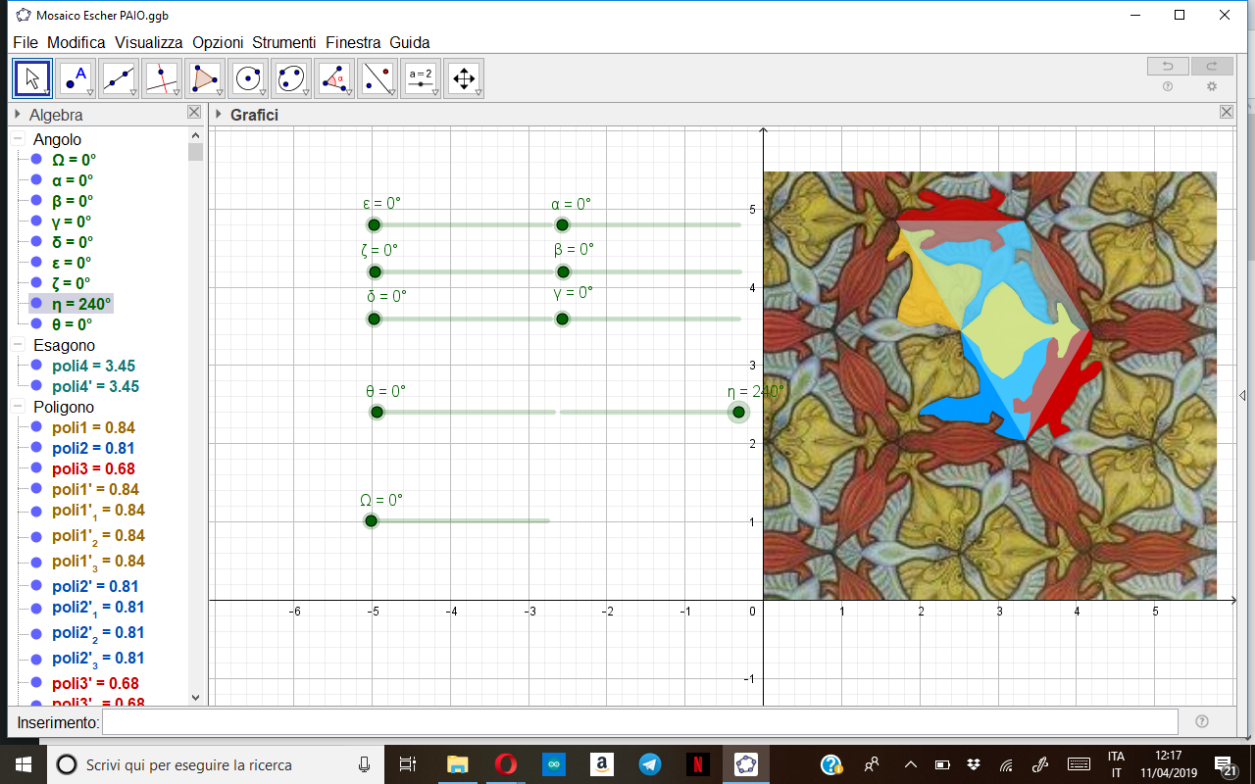
[color=#ff0000][b]Rotazione di 240°[/b][/color]
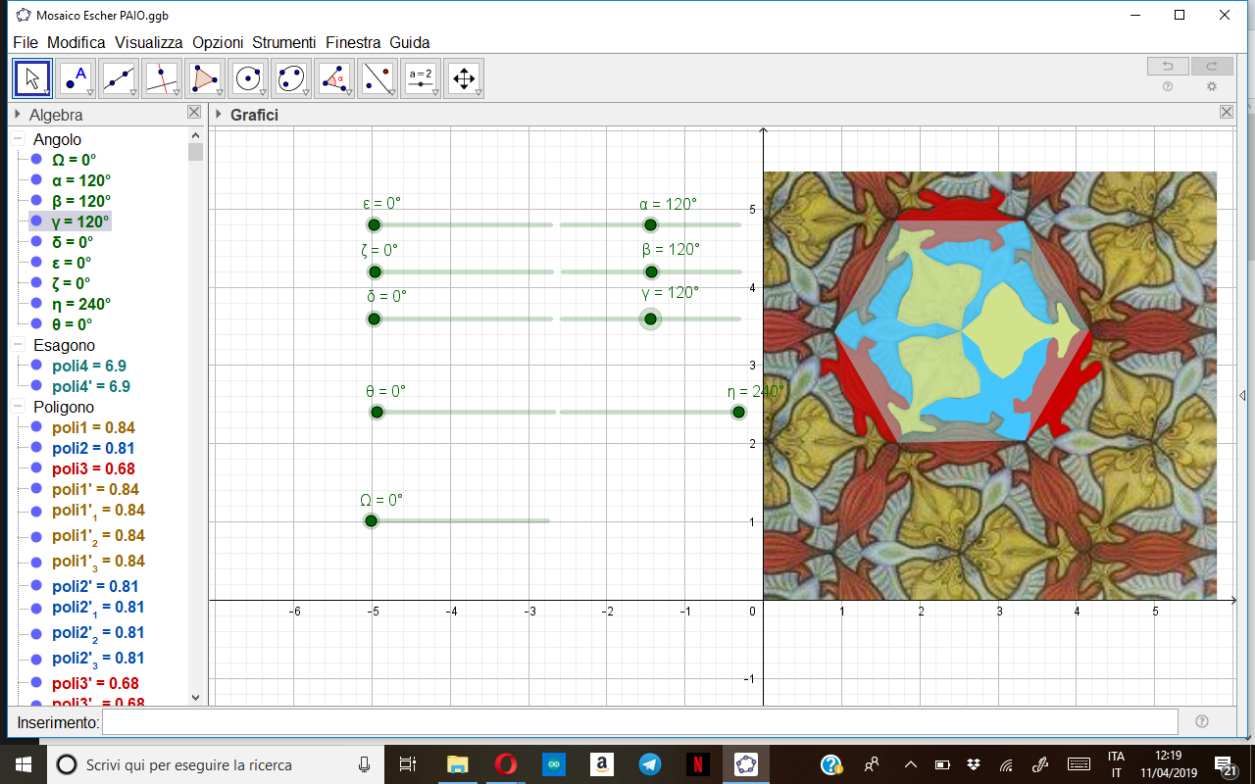
[color=#ff0000][b]Esagono composto dai tre moduli base[/b][/color]
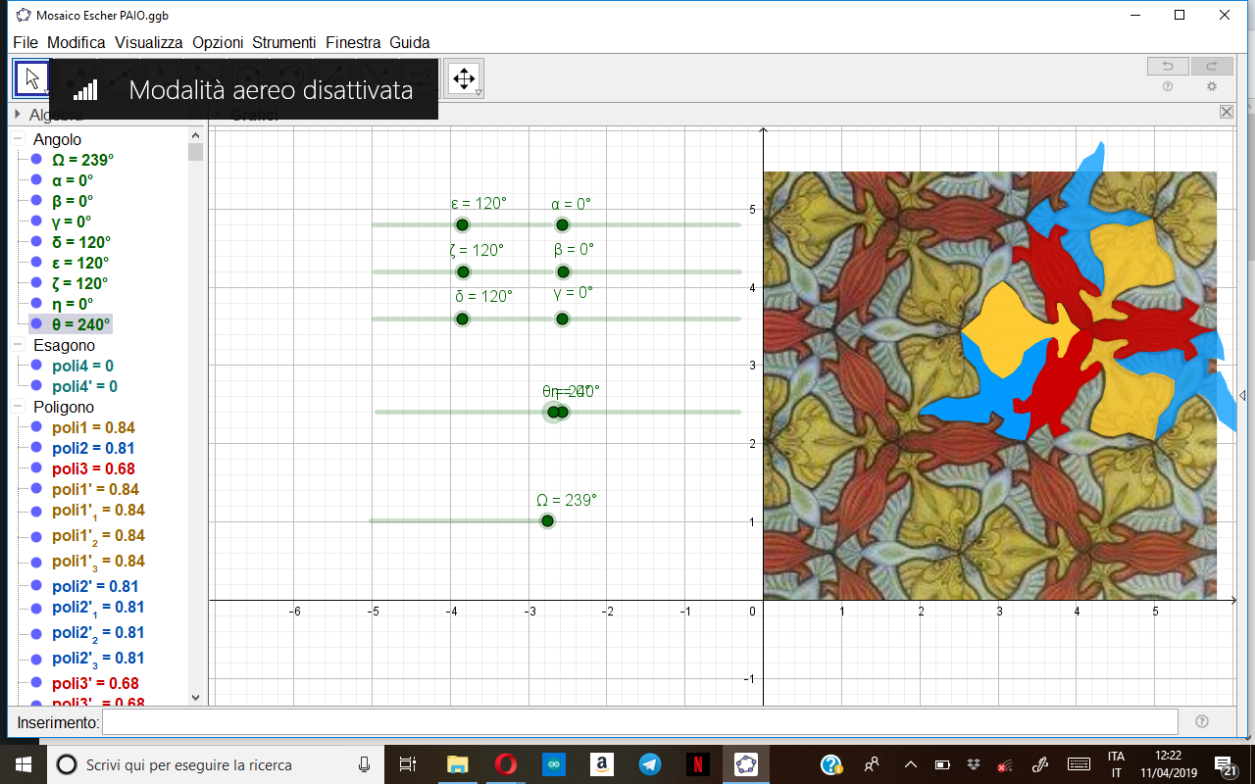
[color=#ff0000][b]Rotazioni di 120° e 240° secondo un altro punto[/b][/color]




