[b]このワークシートは[url=https://www.geogebra.org/m/twxxx3yq]Math by Code[/url]の一部です。[br][br]アプレット、背景、実装の順に見ていきましょう。[br][/b][br]フーリエ変換のよさはオイラーがe[sup]ix[/sup]に三角関数を詰め込んでくれた周期Ｔを∞にすることで、[br]周期的でない波の周波数分析ができるようになることだ。[br][br]しかし、難点は積分と複素数計算が必要になること、そして、関数が連続的であることだ。[br]サンプリングデータはデジタルで、離散量だ。[br][br]そこで、離散フーリエ変換が考案された。今回は離散フーリエ変換とその高速化としてのFFTを調べてみよう。

[b][size=150]＜フーリエ変換をデジタル化しよう＞[br][/size][/b][br][color=#0000ff][b]調べる時間がＴ秒間で、サンプリング間隔がＤ秒だとすると、n=T/D[/b][/color][br]時刻リスト[b][size=150]ts={0,D,2D,....(n-1)D}[/size][/b]に対する[br]f(t)のデータ[b][size=150]x={x0, x1,x2,....x(n-1)}[/size][/b]が得られたとしよう。[br][br]xj=f(jD)という関係ができます。サンプリングなので、f(t)の関数式は不明でもよいでしょう。[br][br]ｆ(t)が連続的なときと同様にxt =...+c[sub]-1[/sub]e[sup]-ik-1t[/sup]+c[sub]0[/sub]+c[sub]1[/sub]e[sup]ik1t[/sup]+......= Σc[sub]n[/sub] e[sup]iknt[/sup](‐∞,∞)とします。[br]たとえば、n=4 のとき、ts={0, D, 2D, 3D}に対して、[b]xt=c[sub]0[/sub]+ c[sub]1[/sub]e[sup]ik1t[/sup]+c[sub]2[/sub]e[sup]ik2t[/sup]+c[sub]3[/sub]e[sup]ik3t[/sup][/b]とおける。[br]T=nDだから、e[sup]ikt[/sup]＝e[sup]i2πt/T[/sup]＝e[sup]i2πt/nD[/sup], t=jDのとき、[b]e[sup]ikjD[/sup][/b]＝e[sup]i2π jD/nD[/sup]＝e[sup]i2πj/n[/sup][sup] [/sup]＝[b]e[sup]i2πj/n[/sup]=(j)[/b]とおこう。[br]つまり、(j)はガウス平面の単位円のn等分のj番目の点です。(j)の共役複素数を(-j)とおこう。[br]n=4なら、{(0),(1),(2),(3),(4),(5),(6),(7),(8),(9)}={1,i,-1,-i, 1,i,-1,-i, 1, i}[br]{(-1),(-2),(-3),(-4),(-5),(-6),(-7),(-8),(-9)}={-i,-1,i, 1, -i,-1,i, 1,-i } [br]この場合は、複素数と共役複素数の積は(i)*(-i)=(i-i)=(0)=1になります。[br]するとn=4なら、[br][color=#0000ff][b]xj=c0(0)+c1(j)+c2(2j)+c3(3j)だから、[br][/b]x0=c0+c1(0)+c2(0)+c3(0)[br]x1=c0+c1(1)+c2(2)+c3(3)[br]x2=c0+c1(2)+c2(4)+c3(6)[sup][br][/sup]x3=c0+c1(3)+c2(6)+c3(9)[sup] [br][/sup][/color]これで、４つの時刻に対する音や波の信号データから、フーリエ係数c0,c1,c2,c3を逆算して、求めることができるはずだ。[br][br]ベクトルと行列で再表現してみよう。[br]この式を、ベクトルA＝[c0,c1,c2,c3]からベクトルx=[x0,x1,x2,x3]を求める[br]かけ算[b]ｘ＝Ａｃ[/b]とするとき、これが[color=#0000ff]逆離散フーリエ変換（[b]IDFT）[/b][/color]で、[br]この逆算の[b]c=A[sup]-1[/sup]x[/b]が[color=#0000ff]離散フーリエ変換([b]DFT[/b])[/color]です。[br]A={{1, 1 , 1 , 1 }, [br] {1, (1),(2),(3)},[br] {1, (2),(4),(6)},[br] {1, (3),(6),(9)}}[br]Aの随伴行列（共役複素数にして転置した行列）B=*Ａは[br]B={{1, 1, 1, 1}, [br] {1,(-1),(-2),(-3)},[br] {1,(-2),(-4),(-6)},[br] {1,(-3),(-6),(-9)}}[br]積BAは、とても特徴的な結果になるね。[br]Bのi行とAのi列の内積は[br](i=1のとき) 1^2+1^2+1^2+1^2=4。[br](i=2のとき) 1*(1)+1*(-1)+2*(-2)+3*(-3)＝1×4=4[br](i=3のとき) 1*(1)+2*(-2)+4*(-4)+6*(-6)＝1×4=4[br](i=4のとき) 1*(1)+3*(-3)+6*(-6)+9*(-9)＝1×4=4[br]つまり、BAの[b][color=#0000ff]対角成分はすべて４[/color][/b]になる。[br][b]Bのj行とAi列の内積は、合同式と同様に(i)=(i+4),番号が2の差の和は(i)+(i+2)=0、[br]番号の定数倍は分配法則のように外に出せる。指数法則が使えて(i)(j)=(i+j)。[br][/b]i=1: (j=2) (0)+(-1)+(-2)+(-3)=(0)+(3)+(2)+(1)=0, (j=3) (0)+(-2)+(-4)+(-6)=2*0=0 (j=4) 3*0=0[br]i=2: (j=3) (0)(0)+(1)(-2)+(2)(-4)+(3)(-6)=(0)(0)+(1-2)+(2-4)+(3-6)= (0)+(3)+(2)+(1)=0[br] (j=4) (0)(0)+(1)(-3)+(2)(-6)+(3)(-9)=(0)(0)+(1)(1)+(2)(2)+(3)(3)= (0)+(2)+(4)+(6)=2*0=0[br]i=3: (j=4) (0)(0)+(2)(-3)+(4)(-6)+(6)(-9)=(0)(0)+(2-3)+(4-6)+(6-9)= (0)+(-1)+(-2)+(-3)=(-1)*0=0[br]一般に、Bj×Ai=(0)(0)+(i)(-j)+(2i)(-2j)+(3i)(-3j)=(0)+(i-j)+(2(i-j))+(3(i-j))=(i-j){(0)+(1)+(2)+(3)}=(i-j)0=0[br]だから、[color=#0000ff][b]対角成分以外の内積は０[/b][/color]になる。[br][br]結局は単位行列をEとすると、[b]BA＝4E[/b]となるね。[br]だから、ｘ＝Acの両辺に左からBをかけると、[br]Bx=BAｃ＝4Ec=4cになる。これから、c=1/4 Bxになる。A[sup]-1[/sup]=1/4Bということだ。

[b][size=150]＜FFTの行列＞[br][/size][/b]離散フーリエ変換と逆変換は、[br]普通のフーリエ変換の発想をデジタルデータでできるようにした点がすばらしい。[br]しかし、弱点がある。[br]n=4のときは、4×4回の複素数のかけ算が必要になる。[b]nの2乗の計算オーダー[/b]は大きすぎる。[br]その弱点を克服するのが[b]高速(fast)フーリエ変換（FFT)[/b]という計算手順だ。[br][br]新しい発想というよりも、アルゴリズムの工夫と考えた方がよいでしょう。[br]n=2,4,8,16と観測範囲Tを等分する数を倍ばいに増やすことで、規則を見つけよう。[br]ベクトルｃ＝[c0,c1,c2,c3,......]、x=[x0,x1,x2,x3,........][br]さらに、[b]4c=X=4[c0,c1,c2,c3,.......]=[X0,X1,X2,X3,..........]とする。Aの随伴行列がB=*A[/b]。[br][b][br]X=Bx（離散フーリエ変換）の行列Bの特徴をさぐろう。[br] [math]\left(\begin{matrix}X0\\X1\\X2\\....\end{matrix}\right)=B\left(\begin{matrix}x0\\x1\\x2\\....\end{matrix}\right)[/math] [br][/b]n=2のとき、行列Bはガウス平面の単位円の正２角形（線分）　の頂点。(0)=1, (1)=-1。[br]合同式のように(i)=(i+2)で、{(0),(1)}={1,-1}[br][math]B=\left(\begin{matrix}\left(0\right),\left(0\right)\\\left(0\right),\left(-1\right)\end{matrix}\right)=\left(\begin{matrix}1,1\\1,\left(1\right)\end{matrix}\right)[/math][br]n=4のとき、行列Bは正４角形の頂点。(0)=1, (1)= i。[br]合同式と同様に(i)=(i+4)で、{(0),(1),(2),(3)}={1,i,-1,-i}[br][math]B=\left(\begin{matrix}\left(0\right),\left(0\right),\left(0\right),\left(0\right)\\\left(0\right),\left(-1\right),\left(-2\right),\left(-3\right)\\\left(0\right),\left(-2\right),\left(-4\right),\left(-6\right)\\\left(0\right),\left(-3\right),\left(-6\right),\left(-9\right)\end{matrix}\right)=\left(\begin{matrix}1,1,1,1\\1,\left(3\right),\left(2\right),\left(1\right)\\1,\left(2\right),\left(0\right),\left(2\right)\\1,\left(1\right),\left(2\right),\left(3\right)\end{matrix}\right)[/math][br]n=8のとき、行列Bは正８角形の頂点。(0)=1,(1)=1/√2(1+i) [br]合同式と同様に(i)=(i+8)で、{(0),(2),(4),(6)}={1,i,-1,-i}[br]B={{(0),(0),(0),(0),(0),(0),(0),(0)}[br] {(0),(-1),(-2),(-3),(-4),(-5),(-6),(-7)},[br] {(0),(-2),(-4),(-6),(-8),(-10),(-12),(-14)},[br] {(0),(-3),(-6),(-9),(-12),(-15),(-18),(-21)},[br] {(0),(-4),(-8),(-12),(-16),(-20),(-24),(-28)},[br] {(0),(-5),(-10),(-15),(-20),(-25),(-30),(-35)},[br] {(0),(-6),(-12),(-18),(-24),(-30),(-36),(-42)},[br] {(0),(-7),(-14),(-21),(-28),(-35),(-42),(-49)}}[br]={{(0),(0),(0),(0),(0),(0),(0),(0)}[br] {(0),(7),(6),(5),(4),(3),(2),(1)},[br] {(0),(6),(4),(2),(0),(6),(4),(2)},[br] {(0),(5),(2),(7),(4),(1),(6),(3)},[br] {(0),(4),(0),(4),(0),(4),(0),(4)},[br] {(0),(3),(6),(1),(4),(7),(2),(5)},[br] {(0),(2),(4),(6),(0),(2),(4),(6)},[br] {(0),(1),(2),(3),(4),(5),(6),(7)}}[br]データ数nは2のp乗。pがビット数。[br](j)はガウス平面での単位円周上の点で,１＋０i を(0)とする、j番目の複素数を表しているね。

[b][size=150]＜FFTの数式の規則性＞[br][/size][/b][b]次は、[/b][b]X=Bx（離散フーリエ変換）の行列Bにx=[{x0},{x1},{x2},{x3},......]をかけたときの数式の規則性を探ろう。[br]・ [size=150]n=2[/size][/b]のとき、(0)=1, (1)=-1で、[br]X=Bｘは、[{X0},{X1}]={{x0+x1, x0+(1)x1}だから、[br][b]X0=x0+x1, X1=x0-x1（和と差）[/b]になる。[br][br]・[b][size=150]n=4[/size][/b]のとき、{(0),(1),(2),(3)}={1,i,-1,-i}で、[br][b][color=#0000ff]正方形の頂点の時計回り[/color][/b][color=#0000ff][b]回転の1個分、回転子w[/b][/color]=(-1)=-i=(3)、w[sup]0[/sup]=1[br]X=Bxは、{{X0},{X1},{X2},{X3}][br]={{x0+x1+x2+x3},(x0+(3)x1+(2)x2+(1)x3},{x0+(2)x1+(0)x2+(2)x3},{x0+(1)x1+(2)x2+(3)x3}}[br]={{x0+x1+x2+x3},(x0-ix1-x2+ix3},{x0 - x1 +x2 - x3},{x0+x1i-x2-ix3}}[br]={{(x0+x2)+(x1+x3)},{(x0-x2) +w(x1-x3)},{(x0 +x2)- (x1+x3)},{(x0-x2)-w(x1-x3)}}[br]{{X0},{X1},[br]{X2},{X3}}[br]={{(x0+x2)+(x1+x3)},{(x0-x2) +w(x1-x3)},[br] {(x0 +x2)- (x1+x3)},{(x0-x2) -w(x1-x3)}}[br]{X0},{X2}だけ見ると、x=[x0,x1,x2,x3}=>L={x0,x1},R={x2,x3}のようにｘを前半Lと後半Rに分ける。[br][b]対応する番号どうしの和、(x0+x2)と(x1+x3)[/b]を求めた上で、さらに（和と差）を求めている。[br]これはn=2と同じ。[br]{X1},{X3}だけ見ると、x=[x0,x1,x2,x3}=>L={x0,x1},R={x2,x3}[br][b]対応する番号どうしの差,(x0-x2)、(x1-x3)それぞれのw[sup]0[/sup]、w[sup]1[/sup][/b]倍求めて、（和と差）を求めている。[br][br]・[b][size=150]n=8[/size][/b]のとき、行列Bは正８角形の頂点。(0)=1,(1)=1/√2(1+i) 、{(0),(2),(4),(6)}={1,i,-1,-i}[br]Bｘ={{X0},{X1},{X2},{X3},{X4},{X5},{X6},{X7}][br]={{x0+x1+x2+x3+x4+x5+x6+x7}[br] {x0+(7)x1+(6)x2+(5)x3+(4)x4+(3)x5+(2)x6+(1)x7},[br] {x0-ix1-x2+ix3+x4-ix5-x6+ix7},[br] {x0+(5)x1+(2)x2+(7)x3+(4)x4+(1)x5+(6)x6+(3)x7},[br] {x0- x1+ x2 - x3 + x4 - x5 + x6 -x7},[br] {x0+(3)x1+(6)x2+(1)x3+(4)x4+(7)x5+(2)x6+(5)x7},[br] {x0+ix1-x2-ix3+x4+ix5-x6-ix7},[br] {x0+(1)x1+(2)x2+(3)x3+(4)x4+(5)x5+(6)x6+(7)x7}}[br]{{X0},{X2},[br]{X4},{X6}}[br]={{x0+x1+x2+x3+x4+x5+x6+x7}, {x0-ix1-x2+ix3+x4-ix5-x6+ix7},[br] {x0- x1+ x2 -x3+x4 -x5 + x6 -x7}, {x0+ix1-x2-ix3+x4+ix5-x6-ix7},[br]={{[(x0+x4)+(x2+x6)]+[(x1+x5)+(x3+x7)]}, {w[sup]0[/sup][(x0+x4)-(x2+x6)]+w[sup]1[/sup][(x1+x5)-(x3+x7)]},[br] {([x0+x4)+ (x2+ x6)]- [(x1+x3) +(x5+x7)]}}, {w[sup]0[/sup][(x0+x4)-(x2+x6)]-w[sup]1[/sup][(x1+x5)-(x3+x7)]},[br]{X0},{X4}だけ見ると、x=[x0,x1,x2,....,x7}=>L={x0,x1,x2,x3},R={x4,x5,x6,x7}のようにｘをLとRに2分して、[br]対応する番号どうしの[b]和リスト{(x0+x4),(x1+x5),(x2+x6),(x3+x7)}をLとRに分け、[/b]n=4のように対応する順に和(x0+x4)+(x2+x6)]と[(x1+x5)+(x3+x7)]を求め、さらにn=2のように和と差を求めています。[br]{X2},{X6}も{(x0+x4),(x1+x5),(x2+x6),(x3+x7)}をLとRに分けるところまでは、同じでn=4のように対応する順に差のw0倍とw1倍を求めて、n=2のように和と差を求めています。[br] [b][color=#0000ff]正８角形の時計回りの回転の1個分、回転子p[/color][/b]=(-1)=1/√2(1-i)[br]{(0),(1),(2),(3),(4),(5),(6),(7)}={p0,p7,p6,p5,p4,p3,p2,p1}={p0,-p3,-p2,-p1,-p0,p3,p2,p1}[br]={1, -p3, -p2=i , -p1, -1,p3, p2=-i, p1 } , p3=p1*p2=p1*w[br]{{X1},{X3},[br]{X5},{X7}}[br]= {x0+(7)x1+(6)x2+(5)x3+(4)x4+(3)x5+(2)x6+(1)x7}, {x0+(5)x1+(2)x2+(7)x3+(4)x4+(1)x5+(6)x6+(3)x7},[br] {x0+(3)x1+(6)x2+(1)x3+(4)x4+(7)x5+(2)x6+(5)x7}, {x0+(1)x1+(2)x2+(3)x3+(4)x4+(5)x5+(6)x6+(7)x7}}[br]= {x0+p1x1+p2x2+p3x3-x4-p1x5-p2x6-p3x7}, {x0+p3x1-p2x2+p1x3-x4-p3x5+p2x6-p1x7},[br] {x0-p1x1+p2x2-p3x3-x4+p1x5-p2x6+p3x7}, {x0-p3x1-p2x2-p1x3-x4+p3x5+p2x6+p1x7}}[br]= {[(x0-x4)+p2(x2-x6)]+[p1(x1-x5)+p3(x3-x7)}, {w0[(x0-x4)-p2(x2-x6)]+w1[p1(x1-x5)+p3(x3-x7)]},[br] {[(x0-x4) +p2(x2-x6)]-[p1(x1-x5) +p3(x3-x7)]}, {w0[(x0-x4)-p2(x2-x6)]-w1[p1(x1-x5)+p3(x3-x7)]}}[br][br]{X1},{X5}だけ見ると、x=[x0,x1,x2,....,x7}=>L={x0,x1,x2,x3},R={x4,x5,x6,x7}のようにｘをLとRに2分して、[br]対応する番号どうしの差(x0-x4),(x1-x5),(x2-x6),(x3ーx7)にそれぞれのp0,p1,p2,p3倍を求めます。その4項目をLとRに分けて、n=4のように対応する和[p0(x0-x4)+p2(x2-x6)],[p1(x1-x5)+p3(x3ーx7)]を求めてから、n=2のように和と差を求めています。[br]{X3},{X7}だけ見ても同様で、n=4の段階で対応する順に差のw0倍とw1倍を求めて、n=2のように和と差を求めています。[br][br][b]こうしてみると、FFTのアルゴリズムの基本は、[br]ｘをLとRに分けて、対応する番号順の和と差にし、[br]差については、回転子にリストの番号乗をしてかけることです。[/b][br]これをn=8,n=4,n=2に対して再帰的に実行しよう。[br]すると、[br][color=#0000ff][b]時間順に区切った音波の振幅データx=[x0,x1,x2,x3,x4,x5,x6,x7]に対してX=[X0,X4,X2,X6,X1,X5,X3,X7][/b][/color]を順に求めることができますね。[br]このインデックスの入れ替わりは2進数にしたときに左右逆転する数同士になっていることを使うと、[br]計算で求めることもできるはず。[br][br]このXをインデックス順に並べ替えることで、[br][X0,X1,X2,X3,X4,X5,X6,X7]が周波数を小さい順にならべた周波数特性のデータになります。[br][br]FFTを使うと、たとえば、n=8の場合複素数のかけ算が8*8=64個出てきます。[br]n=4にsizeダウンしたことで、8/2=4個。n=2にサイズダウンしたことで、4/2=2個を2回。[br]結果として、4+2*2=4×2=8個ですみます。[br]一般に、サイズがnなら複素数のかけ算の回数がn^2回からFFTでn/2×(log2(n)-1)回に激減します。[br]N*NのオーダーからN*logNのオーダーに減るということですね。

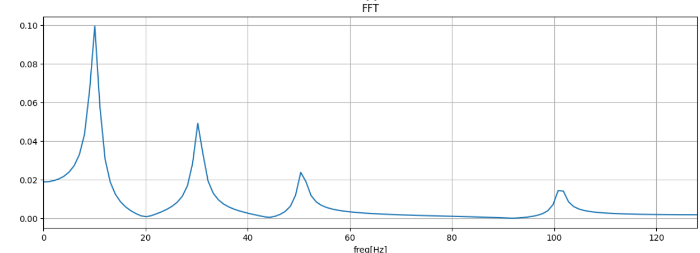
[b][color=#9900ff][u][size=150]質問：FFTをpythonで実装するにはどうしたらよいでしょうか。[br][/size][/u][/color][/b][br]FFTの核心となる関数を作りましょう。[br]FFTのロジック、音声データlstとインデックスnumsを受け取り、どんどん2等分、対応する順に和データと差データを作る関数[b][color=#0000ff]sizeDown[/color][/b]です。[br]lstのサイズsegから、その半分のサイズsubsize=seg/2を得ます。[br]lstの0番以上subsize未満、つまり前半をLとします。[br]L=lst[ :subsize]です。同じように、残り半分がR=lst[subsize: ]です。[br]（最初のインデックスnumsも左と右に2等分して、後々まで引き継げるようにして、渡します。）[br]このLとRをジッパーのように、[b]対応する順の和リストLA=[l+r for l,r in zip(l,r)][/b]を求めましょう。[b][br]同様に差のリストRdif=[l-r for l,r zip(l,r)][/b]を求めましょう。[br]ただし、差の方は、三角関数を使って、[b]回転子w=e ^(- 2pi / seg)[/b] のｋ乗を求める無名関数wを作っておいて指数を求めるための０から始まるインデックスnumを作ります。[br][b]RM=[r*(w(idx)) for r, idx in zip( Rdif, num)][br]これで、下半分のリストができました。[br][/b]あとは、再帰関数としてどんどんサイズを半分して計算します。[br]再帰関数の[b]脱出条件はサイズseg==1[/b]です。[br]1個になったら最初にもらったインデックス番号リストnumsの内容[0]を受け取り、[br]その番号をビット反転関数bit_revにより、入れ替わってしまったXの番号で、データを[color=#0000ff]辞書resltX[/color]に記録しましょう。[br][br]全体の流れは[b][color=#0000ff]FFT[/color][/b]関数で作ります。[br]　うけとった波形データをtargetとしてうけとったら、サイズN = len(target)を求めます。[br]　Nを使って、０からN-1までの調査データにインデックスをつけるためのリストnumsを用意します。[br]　データ数は２のべき乗なので、２の何乗かを bits = int(np.log2(N))で求めましょう。[br]　sizeDown関数にtargetデータ,インデックスリストnums,ビット数bits,　計算結果辞書fftDictを渡します。[br]　処理の結果はfftDictで参照されるため、あとは計算結果辞書fftDictを正しい順にします。[br]　FFTは調査時間が長いと周波数の小さい部分の振幅が大きくなりすぎるので、[br]　データ数Nで割って正規化しましょう。[br][br]実際に色々やってみると、微小な虚部がじゃまだったり、必要以上に表示の桁数が増えて[br]　データの可読性が下がるために[b]to_real関数[/b]で小数点以下の桁数をけずっています。[br][b]ビット反転はbit_rev（n, bits)関数[/b]でやります。[br] bitsは2進数にしたときの桁数です。たとえば、n=3,bits=3とすると、[br] n=3は2進数では、n=011です。[br] これをreturn で110(つまり6）が返ればよいですね。for i in range(bits)で３けた分、[br] i=0,1,2動かして調べます。[br]　n>>i はiけた右にずらすので、011, 001, 000となります。[br]　& 001をしてtrueになるのは、1の位が１のときですから、i=0,1で通ります。[br]　result |= 1 << (bits - 1 - i) はreult or 1 << (bits - 1 - i)でresultを更新していきます。[br]　i=0 では、1<<(3-1-0) で1=001を左に2シフトし、100にします。[br]　この100を、初期値のresult=000とorでけたごとに１を上書きするので、result=100です。[br] i=1では、 1<<(3-1-1)で1=001を左に１シフトし、010にします。[br]　この010の1をresultに上書きするから、result=100 or 010 = 110　[br]　これで、ｎにある１を下の位からみつけて、[br]　あれば、それを反対の位に移動していることがわかります[br]　ｎの「１」が、０位　　...... i 位...... (bits-1)位まで動くとき、[br]　その移動先は、(bits-1)位…（bits-1 -i)位 .. ....０位になります。[br]　つまり、移動前の位と移動後の位の和が一定になることがわかりますね。[br]　これで、ビットの左右が逆転することが確認できました。[br]グラフ作成[br]　時間領域では、時刻データｔぜんぶとその波形データsignalをぜんぶ使います。[br]　n = len(signal)がデータ数です。[br]　周波数領域では、最大周波数をfreqmax = sampling_rate / 2にしましょう。[br]　線対称なグラフになるだけなので、情報量の関係で半分の範囲で十分です。[br]　表示データ数は半分になりました。だから、これに対応して、プロットする範囲を[:n//2]にします。[br] それに連動して、周波数軸を0からfreqmaxをnではなく、n//2で割ります。[br][color=#0000ff][IN]Python===================================[br][/color][b]import matplotlib.pyplot as plt[br]from numpy import cos, sin, pi, exp, log2[br]import numpy as np[br][/b][color=#0000ff]# 微小な虚部を切り捨てて実数を返す。[br][/color][b]def to_real(z, precision=8):[br][/b] return float(int(z.real * (10**precision))) / (10**precision)[br][color=#0000ff]#ビット反転により、指定桁数で2進数の左右逆の番号に変換して10進数にもどす。[br][/color][b]def bit_rev(n, bits):[br][/b] result = 0[br] for i in range(bits):[br] if (n >> i) & 1:[br] result |= 1 << (bits - 1 - i)[br] return result[br][color=#0000ff]#FFTの核心部分[br][/color][b]def sizeDown(lst,nums,bits,resultX):[br][/b] seg = len(nums)[br] if seg ==1:[br] resultX[bit_rev(nums[0],bits)]=lst[0] #ビットリバースしてFFT結果を格納する[br] else:[br] subsize = seg//2[br] L=lst[:subsize][br] R=lst[subsize:][br] numL=nums[:subsize][br] numR=nums[subsize:][br][br] LA = [l+r for l,r in zip(L,R)][br] Rdif = [l-r for l,r in zip(L,R)][br] num = list(range(len(R))) # seg//2のサイズまでの0から始まるインデックスの作成[br] w = lambda k: complex(cos(-2*pi*k/seg),sin(-2*pi*k/seg)) #回転子wのｋ乗を関数化する[br] RM = [ r*(w(idx)) for r,idx in zip(Rdif, num)][br] [br] sizeDown(LA,numL,bits,resultX)[br] sizeDown(RM,numR,bits,resultX)[br][br][color=#0000ff]#FFTの全体の流れ[br][/color][b]def FFT(target, fftDict):[br][/b] #グローバル変数の初期化[br] N = len(target)[br] nums = list(range(N))[br] bits = int(np.log2(N))[br] sizeDown(target,nums,bits,fftDict)[br] srt = sorted(fftDict.items()) #ビットリバースされた順番のFFTのデータを正しい順番に並べる[br] res = [v / N for k, v in srt] #振幅をデータ点数で正規化する[br] return res[br][color=#0000ff]#======================= ここからが設定と視覚化============================[br]# 音データ[/color][br][b][color=#ff0000]sampling_rate = 256 #２のべき乗[br][/color][/b]T = 1.0 #時間領域の調査期間[br]num_samples = int(sampling_rate * T) #サンプル数[br]t = np.linspace(0, T, num_samples) #時間領域の調査時刻リスト[br]frq = 2 * pi * 10 * t #基本周波数frqは10とする[br]signal = sin(frq) + 1/2* sin(frq * 3) + 1/4* sin(frq * 5) + 1/6* sin(frq *10)[br]signal *= exp(-5 * t) #減衰をかける[br]n = len(signal) #作成データ数[br][br][color=#0000ff]# プロットサイズ[br][/color]plt.figure(figsize=(14, 10))[br][color=#0000ff]# f(t)のグラフ[br][/color]plt.subplot(2, 1, 1)[br]plt.plot(t[: n ], signal)[br]plt.title('signal')[br]plt.xlabel('t[s]')[br]plt.grid(True)[br][br][color=#0000ff]# FFTのグラフ[br][/color]freqmax = sampling_rate / 2 #最大の周波数メモリ[br]yF = FFT(signal,{}) [br]xF = np.linspace(0, freqmax, n // 2) #FFTの周波数軸のメモリリスト[br]plt.subplot(2, 1, 2)[br]plt.plot(xF[: n // 2], np.abs(yF[: n // 2]))[br]plt.title('FFT')[br]plt.xlabel('freq[Hz]')[br]plt.grid(True)[br]plt.xlim(0, freqmax) [br]#[OUT][br]#==============================================[br][br]

[u][b][size=150][color=#9900ff]質問：FFTをgeogebraの中のjavasctiptにするにはどんな準備が必要でしょうか。[br][/color][/size][/b][/u][br]pythonにあって、javascriptにないのが、複素数とzip関数です。また、javascriptとgeogebraをデータ交換する関数も必要です。[br][br]１．複素数クラスで和、差、積、絶対値の計算ができるようにしょう。[br]class Complex{[br]    constructor(a, b){[br]    this.real = a;[br]    this.imag = b;[br]    }[br]    set re(a){ this.real = a; }[br]    get re(){ return this.real; }[br]    set im(a){ this.imag = a; }[br]    get im(){ return this.imag; }[br]    abs(){return Math.sqrt(this.real*this.real+this.imag*this.imag);}[br]    add(a){return new Complex(this.real+a.real, this.imag+a.imag);}[br]    sub(a){return new Complex(this.real-a.real, this.imag-a.imag);}[br]    mul(a){return new Complex(this.real*a.real-this.imag*a.imag, this.real*a.imag+this.imag*a.real);}[br]}[br]２、複素数リストの２つ読み取りる関数（和、差、積など）を読み取る関数、高階関数で、[br]　zipして演算する関数をカリー化で実現しよう。[br]function Zip(operation) {[br]    return function(arr1, arr2) {[br]        const result = [];[br]        const length = Math.min(arr1.length, arr2.length); [br]        for (let i = 0; i < length; i++) {[br]            if (arr1[i] instanceof Complex  &&  arr2[i] instanceof Complex) {[br]                result.push(operation(arr1[i], arr2[i]));[br]            }[br]        }[br]        return result;[br]    };[br]}[br]const CLadd = Zip((a, b) => a.add(b));[br]const CLdif = Zip((a, b) => a.sub(b));[br]const CLmul = Zip((a, b) => a.mul(b));[br][br]３．リスト操作関連の関数群1,2,3,4[br]1 整数列(0 to n)の作成[br]function range(n){return  [...Array(n).keys()];}[br]2 js実数List をggb実数Listにする書き方はとてもよく使います。 [br]（アプレットオブジェクトがggap、リスト名somelistの場合）[br]ggap.evalCommand(`somelist ={${somelist}}`);[br]${somelist}はsomelistの名前ではなく、データとして読み取ったものをgeogebraの数式に入力します。[br]3 ggb複素数List をjs複素数List(アプレットオブジェクトがggap)にする。[br]function ggbC2jsRList(ggbListName,Listsize,ggap){[br]    let jsTarget=[];[br]    for (let i=0; i<Listsize; i++ ){[br]        let citem = new Complex(ggap.getListValue(ggbListName, i+1),0)[br]        jsTarget.push(citem);//geogebraのインデックスは1スタート[br]    }[br]    return jsTarget;[br]}[br]4  ガウス平面のｎ等分点の複素数e^2πk/n（左回りにｋ番目）を作成する。[br]function eZ(k,n){return new Complex(Math.cos(2*Math.PI*k/n),Math.sin(2*Math.PI*k/n));}[br][br]

[color=#9900ff][b][u][size=150]質問：geogebraでFFTを作るにはどうしたらよいでしょう。[br][/size][/u][/b][/color][br]バグ取りも含めたコードなので冗長ですが、[br]たとえば、以下のようになります。[br][br]時間領域ボタン、周波数領域のボタン、ビット増加ボタン、ビット減少ボタンをアプレット領域に貼ります。それぞ、ボタンをクリックすると、[br]timeview, fftview, up,downのjavascriptの関数を呼びだすように、設定のスクリプト記述にかきましょう。[br]そして、グローバルスクリプト記述のところに、[br]以下のコードをはりつければよいですね。[br]動きを確認できたら、アプレット自体をダウンロードして、改良してみてください。[br][br]//global [br]let ggap;[br]let width;[br]let height;[br]let sampling_rate;[br]let fftDict;[br]let xlim;[br]let ylim;[br]let bits;[br]let choice;[br][br]function ggbOnInit() {[br]ggap = window.ggbApplet;[br]width = 1.0;[br]height = 2.0;[br]sampling_rate=3;[br]fftDict= {};[br]xlim = 2.0;[br]ylim = 1.0;[br]bits = 3;[br]choice = 0;[br] setup();[br] timeview();[br]}[br]'use strict';[br]//複素数の和、差、積[br]class Complex{[br] constructor(a, b){[br] this.real = a;[br] this.imag = b;[br] }[br] set re(a){ this.real = a; }[br] get re(){ return this.real; }[br] set im(a){ this.imag = a; }[br] get im(){ return this.imag; }[br] abs(){return Math.sqrt(this.real*this.real+this.imag*this.imag);}[br] add(a){return new Complex(this.real+a.real, this.imag+a.imag);}[br] sub(a){return new Complex(this.real-a.real, this.imag-a.imag);}[br] mul(a){return new Complex(this.real*a.real-this.imag*a.imag, this.real*a.imag+this.imag*a.real);}[br]}[br]//複素数リストの要素単位の和、差、積[br]function Zip(operation) {[br] return function(arr1, arr2) {[br] const result = [];[br] const length = Math.min(arr1.length, arr2.length); [br] for (let i = 0; i < length; i++) {[br] if (arr1[i] instanceof Complex && arr2[i] instanceof Complex) {[br] result.push(operation(arr1[i], arr2[i]));[br] }[br] }[br] return result;[br] };[br]}[br]const CLadd = Zip((a, b) => a.add(b));[br]const CLdif = Zip((a, b) => a.sub(b));[br]const CLmul = Zip((a, b) => a.mul(b));[br][br]//リスト操作関連の関数群1,2,3,4[br]//1 整数列(0 to n)の作成[br]function range(n){return [...Array(n).keys()];}[br]//2 js実数List to ggb実数List [br]// （アプレットオブジェクトがggap、リスト名somelistの場合）[br]// ggap.evalCommand(`somelist ={${somelist}}`);[br]//3 ggb複素数List to js複素数List(アプレットオブジェクトがggap)[br]function ggbC2jsRList(ggbListName,Listsize,ggap){[br] let jsTarget=[];[br] for (let i=0; i> i) & 1){[br] result |= 1 << (bits - 1 - i);[br] }[br] }[br] return result;[br]}[br]//FFTの核心部分[br]function sizeDown(lst,nums,bits){[br] let seg = nums.length;[br] if(seg ==1){[br] fftDict[bit_rev(nums[0],bits)]=lst[0];[br] }else{[br] subsize = seg/2;[br] let L = lst.slice(0,subsize);[br] let R = lst.slice(subsize,seg);[br] let numL = nums.slice(0,subsize);[br] let numR = nums.slice(subsize,seg);[br] let LA = CLadd(L,R,subsize);[br] let Rdif = CLdif(L,R,subsize);[br] let w =[];[br] for(let i = 0; i < subsize; i++){[br] let citem = eZ(-i,seg);[br] w.push(citem);[br] }[br] let RM = CLmul(Rdif, w,subsize);[br] sizeDown(LA,numL,bits);[br] sizeDown(RM,numR,bits);[br] }[br]}[br][br]function setup() {[br] sampling_rate = Math.pow(2,bits); //２のべき乗[br] let sampleSize = sampling_rate; //サンプル数[br] let intsample = range(sampleSize);[br] let t = intsample.map((x) => x/sampleSize);[br] let frq =t.map((val) => 2 * Math.PI * 10 * val);[br] ggap.evalCommand(`t={${t}}`);[br] ggap.evalCommand(`frq={${frq}}`);[br] ggap.evalCommand("oto=Zip(sin(v)+1/2*sin(3*v)+1/4*sin(5*v)+1/6*sin(10*v),v,frq)");[br] ggap.evalCommand("mult=Zip(e^(-5*k),k,t)");[br] ggap.evalCommand("signal= oto*mult");[br] ggap.evalCommand("pnts=Zip((a,b),a,t,b,signal)");[br] ggap.evalCommand("graph=Polyline(pnts)");[br] ggap.setVisible("pnts", false);[br] ggap.setVisible("graph", false);[br][br] let n = sampling_rate; //作成データ数[br] let freqmax = n / 2; //最大の周波数メモリ[br] let signal = ggbC2jsRList("signal",n,ggap);[br] let nums = range(n);[br] sizeDown(signal,nums,bits);[br] let yF=[];[br] for(key in fftDict) {[br] yF.push(fftDict[key].abs()/(n/2)); [br] }[br] let fftY = yF.slice(0,freqmax);[br] ggap.evalCommand(`fftY={${fftY}}`);[br] let xF = range(freqmax);[br] let fftX = xF.slice(0,freqmax);[br] ggap.evalCommand(`fftX={${fftX}}`);[br] ggap.evalCommand("fftpnt=Zip((a,b),a,fftX,b,fftY)");[br] ggap.evalCommand("fftgrf=Polyline(fftpnt)");[br][br] ggap.setVisible("fftpnt", false);[br] ggap.setVisible("fftgrf", false);[br][br]}[br]function timeview(){[br] choice =1;[br] bits = 3;[br]alert("timeview called. choice: " + choice + ", bits: " + bits);[br]if (!ggap) { // ggapが未定義またはnullの場合[br]ggap = window.ggbApplet;[br] }[br] setup();[br] ggap.setVisible("graph", true);[br] ggap.setVisible("fftgrf", false);[br] sampling_rate = Math.pow(2,bits); //２のべき乗[br] sampleSize = sampling_rate; //サンプル数[br] xlim = width/2;[br] ylim = height;[br] ggap.setCoordSystem(0, xlim, - ylim, ylim);[br]}[br][br]function fftview(){[br] choice =2;[br] bits = 3;[br]alert("timeview called. choice: " + choice + ", bits: " + bits); [br]if (!ggap) { // ggapが未定義またはnullの場合[br]ggap = window.ggbApplet;[br] }[br] setup();[br] ggap.setVisible("graph", false);[br] ggap.setVisible("fftgrf", true);[br] let n = sampling_rate; //作成データ数[br] let freqmax = n / 2; //最大の周波数メモリ[br] xlim = freqmax;[br] ylim = height/10;[br] ggap.setCoordSystem(0, xlim, - ylim, ylim);[br]}[br][br]function up() {[br] bits +=1;[br]alert("timeview called. choice: " + choice + ", bits: " + bits);[br]if (!ggap) { // ggapが未定義またはnullの場合[br]ggap = window.ggbApplet;[br] }[br] setup();[br] console.log(sampling_rate);[br] redraw();[br]}[br]function down(){[br] bits -=1;[br]alert("timeview called. choice: " + choice + ", bits: " + bits);[br]if (!ggap) { // ggapが未定義またはnullの場合[br]ggap = window.ggbApplet;[br] }[br] setup();[br] console.log(sampling_rate);[br] redraw();[br]}[br][br]function redraw(){[br]if (!ggap) { // ggapが未定義またはnullの場合[br]ggap = window.ggbApplet;[br] }[br] setup();[br] if (choice==1){[br] ggap.setVisible("graph", true);[br] ggap.setVisible("fftgrf", false);[br] xlim = width/2;[br] ylim = height;[br] }else if(choice==2){[br] ggap.setVisible("graph", false);[br] ggap.setVisible("fftgrf", true);[br] let n = sampling_rate; //作成データ数[br] let freqmax = n / 2; //最大の周波数メモリ[br] xlim = freqmax;[br] ylim = height/10;[br] } [br] ggap.setCoordSystem(0, xlim, - ylim, ylim);[br]}[br][br]