GeoGebra gebruiken
Kopieer dit boek niet a.u.b. Dit boek is een initiatiehandleiding en een 'work in progress'. Het wordt nog aangepast en uitgebreid en de recentste versie vind je altijd in de reeks Initiatiehandleidingen op de openingspagina van GeoGebra. Nieuws over GeoGebra vind je verder ook op de facebookpagina van [url=https://www.facebook.com/GeoGebra-Vlaanderen-106036888566979]GeoGebra Vlaanderen[/url]. GeoGebra leren werken als leraar wordt meer en meer een tweesporenopdracht. Leraren leerden met GeoGebra werken als tool om afbeeldingen te maken voor toetsen en examens en om toonbestanden te maken voo hun lessen. Meer en meer profileert GeoGebra zich echter ook als een grafische rekenmachine voor dagelijks gebruik door leerlingen in de klas. Hoe je GeoGebra ook gebruikt, hou tool en doel gescheiden. GeoGebra is een tool om wiskunde te leren en onderwijzen Bekijk zeker ook volgende initiatiehandleidingen. Je vindt ze gegroepeerd in het hulpcentrum van GeoGebra (link onderaan op de openingspagina). - Leer in [url=https://www.geogebra.org/m/tsxf93qn]Online GeoGebra materiaal[/url] hoe je GeoGebra bestanden kunt uploaden naar het online materialenplatform en in online werkbladen applets kunt aanvullen met afbeeldingen, filmpjes, open vragen en meerkeuzevragen. - Leer hoe je GeoGebra kunt gebruiken als beveiligde grafische rekenmachine in de [url=https://www.geogebra.org/m/scntsjc9]Examenmodus[/url]. - Leer hoe je de toepassing [url=https://www.geogebra.org/m/by259cz7]GeoGebra Klaslokaal[/url] kunt gebruiken om zowel in contactonderwijs als afstandsleren de vorderingen van je leerlingen in realtime op te volgen. - Leer hoe je [url=https://www.geogebra.org/m/ca4qynme]GeoGebra Notitieblok[/url] als whiteboard kunt gebruiken om te tekenen, formules of tekst te typen, afbeeldingen in te voegen of een GeoGebra scherm te openen om er actief in te werken.
Table of Contents
- applets en versies
- uitwerking 1
- uitwerking 2
- uitwerking 3
- f(x) = ax in de Suite app
- GeoGebra CAS
- algebraïsche invoer
- numeriek toetsenbord
- functietoetsenbord
- lettertoetsenbord
- symbolisch toetsenbord
- ingebouwde functies en commando's
- functies
- Bijzondere punten
- GeoGebra versies
- topvergelijking van een parabool
- Labels van punten - exacte waarde van nulwaarden
- De assen en het rooster
- schuifknoppen voor parameters
- Begrensde oppervlakte
- getallen
- repeterende decimale getallen
- ongelijkheden oplossen
- CAS: oplossen van stelsels
- Rijen
- statistiek
- tabelvenster: losse gegevens invoeren
- tabelvenster: frequentietabellen
- tabelvenster: gegevens in een frequentietabel
- tabelvenster: importeren van csv-databestanden
- rekenblad in Suite
- rekenblad: databestand - gegevens klaarzetten
- rekenblad: volledige frequentietabel
- rekenblad: genormaliseerd histogram
- De module statistiek in Klassiek
- spreidingstabellen: tabelvenster
- spreidingstabellen: Klassiek
- Normaalverdeling: in app of tekenvenster
- QQplot (kwantielplot) als controle van normaliteit
- binomiale verdeling in app en commando's
- Z-Toets van een gemiddelde uitvoeren en interpreteren
- Z-Toets van een proportie uitvoeren en interpreteren
- T-Toets van een gemiddelde uitvoeren en interpreteren
- betrouwbaarheidsintervallen
- ruimtemeetkunde
- Punten, lijnstukken, rechten en veelhoeken in de ruimte
- Ruimtelichamen, vlakken en onderlinge ligging
- omwentelingslichamen
- Analytische ruimtemeetkunde
- Vergelijking van een vlak met matrix in CAS
- matrices, vectoren, complexe getallen, grafen
- Werken met matrices
- matrices in breukvorm
- Oplossen van stelsels: grafisch of met matrices
- rijoperaties met matrices
- Een matrix en zijn inverse matrix
- Vectoren
- Complexe getallen
- Graph Online
- toonmateriaal
- analyse - werken met twee tekenvensters
- Labels en markeringen
- 7 begrip afgeleide - afgeleide functie
- 8 sinusfunctie en goniometrische cirkel
- 9 colaflesje
- placeholders
- GG toepassingen
- GeoGebra in toetsen en examens
- Online GeoGebramateriaal
- GeoGebra Klaslokaal
- GeoGebra Notitieblok
- Ontwerpen voor gevorderden
- aanvinkvakjes
- klaarzetten i.p.v. tonen
- schuifknop
- dynamische transformatie
- transformaties combineren
- meetkundig bewijs van de stelling van Pythagoras
- dynamische ilustratie van het bewijs
- animatie met start-pauze-resetknoppen
uitwerking 1
Deze uitwerking werpt meteen alles op tafel. [br]Het is een prima applet als samenvatting, maar wellicht net iets minder geschikt om te gebruiken bij het aanbrengen van de kenmerken van f(x) = ax als nieuwe leerstof
tips
[list][*]Definieer je de functie f als [b]f(x)=Veeltermfunctie(a x)[/b] i.p.v. als f(x)=a x, dan vermijd je dat het voorschrift in een tekst op je tekenvenster getoond wordt als f(x) = 0x of f(x)=1x.[/*][*]Een tabel kan je als een tekst creëren vanuit het rekenblad. In de definitie van de tekst kan je achteraan zowel de uitlijning van de waarden kiezen als bepalen welke lijntjes al dan niet getoond worden.[br]Zie hiervoor in de handleiding het commando [url=https://wiki.geogebra.org/nl/TabeLT_Commando]TabeLT Commando[/url].[/*][/list]
numeriek toetsenbord
interessante toetsen op het numeriek toetsenbord
[list][*]de constanten [math]\pi[/math] en e zijn ingebouwd in GeoGebra.[br][u]Opmerkingen[/u]: [br]GeoGebra herkent [math]\pi[/math] ook als je gewoon [i]pi[/i] of [i]PI[/i] typt.[br]GeoGebra herkent [math]e[/math] enkel als de constante van Euler als e niet eerder gebruikt werd als een objectnaam.[/*][*]Werken met machten en wortels:[table][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFEAAAA0CAYAAADyttTfAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAMFSURBVHhe7dsxTuNAFAbgf+zYJtJuR8clEBUSFDkFFLkAEhUXAAFnQOIAHMV0uYArJIoNWlqMMx7bb4tgEw/jrEMcx0bvkyyZN5OCX2/8okgWL9NXEkIAQgAALGHBcWy47gD2wEZOfKwv3ptqi0y1Kqvs3TbKCHGcQKkUAGDpGzzPgbfjQFj9+afaJiwBb8eB5zmAHqLnOnDcz+5jyzmuDc9zPkN0BjYH+A2Oa3+G6LqD8iqrzQKAwcDmZ+AaLACwB1/mC1vBPESLQ1yHhY+RnSMi4/13rPv5vvgRLRgEAfb39yGEgBACZ2dniKJI37YxvQ8xCAKcnp7i7u4ORAQiwt7eHi4uLloLsvchTiYTHB4e4uDgoKidnJzg6ekJz8/Ppb2b0vsQx+Mx7u/vMRwO9aXW9D5Ek8lkAiEEdnd39aWNEC/TV/r1e1j6ZabqvvjQkpquqq6ru+9/Hh8fcXx8DN/3cXR0pC9vxI/qxDzAh4eH1gLENjrx5uamuL+8vPxSu7q6AgBcX1/XquUWAxyPx6W1jXuZvtLb2xuFYUhhGNL7+ztFUURRFNFsNiMpJUkpKY7j4lJKkVKKkiQprjRNjVeWZaVrNBoRABqNRsZarm6NiMj3fQJAvu+X6m3p/XEOggDn5+etPgN1rR/nKnX36W5vb4vHgq6tYHsfYhe0HqJpsMCwz2TZYNmqLgyWLMv0Z7VR1WDZtt4Pli5o/ThXqbuvi7gTG1B0IhY6z9SJ+d+L9/rfJnr9Rw+WfLhUDRbTcOHBMsfHuQGtH+cqdfd1EXdiA1rvRNNgaeKnsK3qwmAxDYy6tS7g49yA1o9zlbr7uog7sQEcYgM4xAZwiA3gEBtgAfP3Mtj3WQCQZpleZyuYh5hwiOuwiAhJkvKRXkMxWOI4Ka+w2ooQkySFiucv/LH6VJyWv+LIWHGQK1BxCinV1++JUirImeJn5BKUEeRMQUoFVH3ZVipFGErImeKh84Gy+QCWM4UwlMW7zgAgpn/+kpW/USUEBPinsFUZO5GthkNswD91Aqp9Fk5KGAAAAABJRU5ErkJggg==[/img][/td][td]Typ het grondtal en klik vervolgens op de toets om het kwadraat te berekenen.[br][br][/td][/tr][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAAuCAYAAAC7zE4hAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAGTSURBVGhD7dfBcYMwEAXQlYXkHJIeKMEdQCluI5kcKIUSKIka7INnkEG+JLIhiseKlsij+e/GanT5s8uCOB5OljyUkqR1QWIjlkfwxU6WhuFMxowkfEFut4qUlssy/MIMI22WRYQYTmk5D1IpiRD/aBak1sXtIwRwQSolsVgiuCBl8eN1CQGuQW4QZAyXHsY6TlZt2DQNCSFIiGtT+GpryCrIlOTH+2dDRKS3eXz6lGVJdV1TXdd3a9zcL+Lr28vyDAJgtJlkFaRvsfhqa8gqyJSSLZu2banrOur7nna7XXTtm2+x+GrsjoeTPR5O9r9VVWWJyFZVxVJLDaPNBJ8/TNCRTJJ1ZNu21Pc9lWVJ+/1+eXxXzN3VPNOyeVTM3bVgtJkkG+3coCOZJOvImIURc3c1WDY8MNpMko12btCRTJJ1pG9hxNSSe6ZlE1NLDaPNJNlo5wYdyQRBMkGQTBAkEwTJxAVpJzs/gSAuyHGa5icQ5BrkGUHGcEEaM2K8I8yWzTCcbx8hwCxIY0Yyw3hbggddADX0aoRkTvYJAAAAAElFTkSuQmCC[/img][/td][td]Typ het grondtal van een macht. Klik vervolgens op de toets om een placeholder te creëren voor de exponent. [br][u]Let op[/u]: de muisaanwijzer blijft in de exponent staan tot je de pijltoets recht indrukt. Dit maakt het mogelijk om in de exponent zelf nog bewerkingen uit te voeren.[/td][/tr][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAE0AAAA1CAYAAAAEeGYcAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAL0SURBVHhe7dk/SyNBGAbwZ2az2SOVYqGFAdFSSKN1FNLb2thYhGDhF1CIpvIDWMXvINHSLp2Q1spCEIlaxeAdcreOu+81d3uXiYm7Y8yO+P5gEN55bR7mXxLx4/tPAktE6gX2Ng7NAIdmQAw601zXgZORcKSEkEKf/lIoJARhiOAlhFJBf2iu6yCbzXz5oAahkHq3p+e58L65HNgQQop/oXmeCzfr9HawV0n82ZIcWHwSALLZjF5nQ0jXdfgMS0g6GX6qJSUdyaElJYjo1cctG4yXmQEOzQCHZoBDM8ChGeDQDFj/5Gi329jY2NDLsTWbTb30fmS5arVKAIzHR7B6pYVhiHw+j7u7OzQaDUxMTOgtb1pdXdVL76enaJNGo0EAqFQq6VOpsvoiqNfrAICtrS19KlXWbs+bmxvMzc1henoat7e3kBZ9sWBtaDs7Ozg4OEC1WkWtVgOA6C8A7O3tJaqNlL5fbaCUoqmpKZJS0v39fVTf39/vuxXj1kbJnjX/n5OTE3Q6HaytrWFmZkafTp+eog1KpRIBoLOzM33KCtadaX8vgHw+j+vrawhh3+8XY9ueQoi+cXp6qrfh8PAQRITt7e2+wGq1WjSGidtnTF96H2VlZSUay8vLBIBmZ2fp6ekp6vF9nyYnJ8nzPOp2uz3/TwkO+Lh9psa20prNZjRarRYKhQLa7TZ2d3ejnuPjY3S7Xayvrxt9ZBobPcVxabVaJIQgx3Ho4uKCiIiKxSIBoPPzc73dKqmFRkRUqVQIAC0tLdHl5SUBoMXFRb3NOqneng8PD5ifn8fj4yMWFhZwdXWFo6MjlMtlvRUY8NKPWxspPcVxq9fr0aGdy+V6Lgbdawd83Nooje0iGKRcLqNQKAAANjc3kcvl9BbrpLo9P6vUV9pnxKEZ4NAMcGgGODQDkkK+PJOSQRjqNfYGGbxwaElJpQLwFk1GAsDz84teZ0NIAFAqgHoO9Dk2QPTk8H3FwcXU807zfQX/l+IzbggKCb8BWhm2fOfdds0AAAAASUVORK5CYII=[/img][/td][td]Klik op de toets vierkantswortel en typ het grondtal om de vierkantswortel te berekenen. [br]Je berekent de vierkantswortel uit 2 ook als [i]sqrt(2)[/i].[br][u]Let op[/u]: de muisaanwijzer blijft in het grondtal staan tot je de pijltoets recht indrukt. Dit maakt het mogelijk om in de exponent zelf nog bewerkingen uit te voeren.[/td][/tr][/table][u]Opmerking[/u]: De toets [i]n-de machtswortel[/i] vind je in het [i]virtuele toetsenbord functies[/i].[/*][/list][br][list][*]Verdere interessante toetsen[br][table][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAAwCAYAAACCEC3KAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAG0SURBVGhD7dtBbsIwEAXQHzuOWbR3gpvlaJwJFihxHHcBCo0bStMZrEk7T0JCY6xIXw4fCaU6ny4JDzhnYWsDawwqU+XL/04aE+I4Ig4jQoiztWopSOcsmqbW8L6RxoS+H6ZATf4B7x38zmmIT1Smgt85eO+APEjvHVxjP4/UE66x8N7dg3TOaoi/5Bp7D7Jp6vmqWsXgdhr1O5HGAICtv3SOWukapNEgqQxuVa5o9Cgy0SCZaJBMqvPpkt7ed/n8ZY7H4/R+v9/P1riVvBbOp0sqCUACkNq2zZfYtW07Xe/V9NZmIibIw+EwvThmpYkJEtl3GsesJFFBLhUCZVaUlg0PUSdyy8QESSkMyl4uYoIEsTAoezmICpJSGJS9LLRseIg6kVsmJkhKYVD2chETJIiFQdnLQVSQlMKg7GWhZcND1IncMjFBLhUGZVaamCDxoDAos5JEBblUGJRZUVo2PESdyC3Tv2OZFA/yr9Jbm4kGyUSDZGKA6zMjisYAQBzHfK5WugY5aJBUBgBCiHp7E01l0/fDfEWtMgUZQkTo5098qp8JfZz//Om6oGGuFPqIrgv4AKSvsmXueVZcAAAAAElFTkSuQmCC[/img][/td][td]Klik op de knop en typ een getal of een uitdrukking om de absolute waarde te berekenen. [br]Je kan de absolute waarde van bv. -2 ook berekenen als [i]abs(-2)[/i] of door zelf de beide verticale streepjes te typen.[/td][/tr][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFMAAAA0CAYAAAD2QwTiAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAH0SURBVHhe7dtBbqMwFMbxZ5uHs5i5Q47AEThKrjGjWcxRcrScoV20YGx3EUIDaaKCn4JFv5+URUzo4q86D0Wyen15iwQi1KOYzIZMocloTUqr6eUfJYZIPgTyXSDn/PQy0b2YzIbKsvjxAe+JIVLbdjdR9egdEVnLZHeMkA8orcjumKzl0fooprVMXJrrJXiASzMKOsRkNgi5AJeGmM/dhphlWVx/Bma4tNPU/1fiO3I5pRUxm3NMU9zMIZjJFLqPqREzldF9TGzxdEqr2+dMWA4xBSGmIMQUhJiCsohZ1zUppZJedV1P/+zTZRFzK9Try1v89Xs3XX+q4/FIp9NpujzLfr+nw+EwXX6qLGJuBba5oCxiXgbQ9RBJWVtLFjG3wvz98+9/adf/YbiqKqrrmqqqEllbAwaQIGxzQVnETBkiKfdKyyLmVmQ9gL4r5V5JGECCsM0FZREzZYik3Csti5hbgQEkCANIELa5oCxifjVEUtbWkkXMrch6AKWsrQEDSBC2uSDEFKSpP9cCaWKI55g+hOk1mMmH0MfsEDOV7/qYznls9QQxRHLOfw6gtu3Gn4Bvu7QbYjrnybVfn1aF+1zrhwOpo0ejpnEIOoNrPTWNG97fPGc2jaPm3eE79IEYIjXvbhSS7p03v8Dh/U+LD+/DMh/1JdLlwjy5wwAAAABJRU5ErkJggg==[/img][/td][td]Deze knop heeft niets te maken met een rekenkundig gemiddelde, maar met decimale getallen met een periode, bijvoorbeeld het getal 2.133... [br][u]Werkwijze[/u]:[br]- Typ alle cijfers voor de periode (hier dus 2.1).[br]- Klik op de toets periode, typ één maal de periode (hier dus 3) en bevestig met enter. Als uitvoer toont GeoGebra het getal in breukvorm, met de optie om het getal ook decimaal te bekijken met de ingestelde nauwkeurigheid.[br][/td][/tr][tr][td][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAAzCAYAAAAEhF9kAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAJkSURBVHhe7duxkaMwFAbgZ7DwBbcV4BRmqIA+nAIlUMDeXHA12CVATB24BWK7ATvwggy6xIttrDtLBlZo530ZP4r+4UkQMDseTgw4CDHBsuYwM2bdW+iCNQyq6gyU1jDjFblYECCW2Y3RP9CqBqMbYonyiGXeF0mIiSW+6K5Iy5rfXiIJbZGEmHiw9NAWac4ftksk4VqkgUX20baHY92Plo9hGIbgui6EYSidjUXLIqfI/PX++w8AgLXQ69XH8zzwfR88z5POxtB+Iv58+9G9hyTgaA9EyyJFDxHRdUPQssgp+laHDY/our6UHDbb7RYAAJbLJdi2LZVN1vFwYsfDiX0lx3GY4zhsvV5LZ1Ol5R7JO0REs7EoKTJJEkiSBFarlXQ2VUr2yL6yLIP9fg+2bbcli2ZjUVKk6CHCW/eZvcL3/W40GCVFuq4LAABxHEMcx93bLd66z+wVRVF0o8Eo2SO/IyVPJG9keXjrcLQHxDtERLPRqHghz/Oc5XnOdruddMYYY0EQMMdxWBAE0tlYlOyRURRBFEWQZZl0NlVKiuwrTVMoigLSNJXOxqJkj/zfIfIsmyolRfYleoiIrhuClqOdZRlsNpune6fouiFoWeQUaTnaU4RP5EC0fCJ5h4hoNhoVXzZ98b5YRLOx4GgPRMvRnqL2iWTNw18iSEJbZN0093eQlGuRZyyyj7ZISmsc7x7uTu2qOt9eIgl3RVJaA63q2wgJeniPLEuKZUri/tQJlzLLD4p75hOsYVB+UChLyv/N+BYhJphzA0zDwH9xLuXVTQP1uQFKr5P7tEgkhjvaSN5fqVHpL+Omk+0AAAAASUVORK5CYII=[/img][/td][td]Met deze toets kan je vlot breuken of rationale vormen invoeren.[br]- Klik op de toets om placeholders te creëren in het algebravenster.[br]Merk op: De muisaanwijzer wordt voor de breuk geplaatst. Dit maakt het mogelijk om oneigenlijke breuken in te voeren zoals [math]1\frac{2}{3}[/math]. Na bevestigen met Enter toont GeoGebra als uitvoer de breuk [math]\frac{5}{3}[/math], met de optie om het resultaat decimaal te tonen.[br]Ook voor het definiëren van rationale functies met langere teller of noemer is deze knop erg handig.[/td][/tr][/table][/*][/list]
Experimenteer in het applet met de knoppen van het numeriek toetsenbord
Bijzondere punten
Bijzondere punten als snelle grafische controle
[list][*]Typ [b]-x³ -3x² + 4[/b] in het invoerveld van het algebra venster en Enter.[/*][*]Je invoer beginnen met '[b][i]f(x) ='[/i][/b] is niet nodig. Het is enkel nodig wanneer je zelf de naam van een object wil bepalen.[/*][*]Bij het invoeren van een functievoorschrift verschijnen de zogenaamde bijzondere punten in het tekenvenster. [br]Dat zijn: de snijpunten met de x-as, het snijpunt met de y-as, de extrema en eventuele perforaties (ophefbare discontinuïteit). Je toont m.a.w. een eventuele perforatie dus gewoon door op de grafiek te klikken. Klik je vervolgens op het punt dan verschijnen ook de coördinaten.[/*][*]Klik je in het tekenvenster, dan worden deze punten verborgen (maar blijven ze wel bepaald).[br]Klik je nadien met je muisaanwijzer op de grafiek, dan verschijnen ze terug. Klik je op een van de punten, dan wordt ook de aard van het punt en zijn coördinaten getoond. Dit is handig voor een snelle verkenning of grafische controle van je berekeningen.[br]Zo zie je bv. dat het punt (-2, 0) zowel een snijpunt met de x-as is als een extremum.[/*][*]Definieer je een tweede functie, dan worden extra ook de snijpunten van de grafieken van beide functies getoond, wat handig is voor de grafische oplossing van stelsels.[/*][/list]
Bijzondere punten in het algebravenster
Je kan de bijzondere punten van een functie ook definiëren als objecten die blijvend getoond worden in het algebravenster en het tekenvenster:[br][list][*]Zowel de offline versie van GeoGebra 6, de websersie als de apps hebben achteraan in elke lijn van het algebra venster een [b]Meer-knop [/b](met drie puntjes als icoon). Klik op deze knop en selecteer [b][i]Bijzondere punten[/i][/b] om de snijpunten met de assen te creëren en de extrema. Je hoeft deze punten dus niet meer apart te berekenen bij het analyseren van het verloop van een functie.[/*][*]Vul deze bijzondere punten zelf nog aan met het commando [b][i]Buigpunten( )[/i][/b] om de eventuele buigpunten te creëren.[/*][*]Eventuele perforaties bereken je met het commando [b][i]OphefbareDiscontinuïteit()[/i][/b].[/*][/list]
functiewaardentabel
In de Suite app vind je in opties van de knop Meer ook de mogelijkheid om een functiewaardentabel te creëren.[br]De ontwikkeling van nieuwe toepassingen in GeoGebra gaan niet meer uit van een tekenprogramma dat je downloadt op een pc, maar van een geavanceerde en intuïtieve online rekenmachine waarmee materiaal online gedeeld wordt. Merk op dat je deze apps kunt downloaden op je smartphone, tablet of pc maar ook online ook kunt gebruiken. [br]Bij het uploaden van een ggb-bestand wordt het applet online opgeslagen in de versie waarin het gemaakt is: Klassiek 5 of 6 wordt bewaard als Klassiek, Suite als Suite. Maar je kan onderaan het applet in de [i]Geavanceerde Instellingen[/i] ook zelf kiezen in welke versie je bestand opgeslagen en getoond wordt. In de initiatiehandleiding [i][url=https://www.geogebra.org/m/tsxf93qn]Online Geogebramateriaal[/url][/i] leer je hier alles over.
Afgeleide functie
[list][*]De afgeleide functie van een functie f creëer je met het commando [b][i]Afgeleide( f )[/i][/b] maar je kunt ook gewoon [b][i]f'[/i][/b] typen in het invoerveld. In beide gevallen krijgt de afgeleide functie als naam f'.[/*][*]De tweede afgeleide bereken je met het commando [b][i]Afgeleide( f, 2)[/i][/b] ofwel door [b][i]f'' [/i][/b]te typen. [br][u]Let op[/u]: Typ twee keer het enkele accentje en gebruik niet het dubbel accentje.[br][/*][*]De functiewaarde voor x = 4 bereken je als [b]f(4)[/b].[br]De waarde van de afgeleide voor x = 4 bereken je als [b]f'(4)[/b].[/*][/list][u]Opmerking[/u]: Je vindt een lijst met alle GeoGebra commando's, gerangschikt per categorie als volgt:[br][list][*]Klik in het invoerveld, daarna op het toetsenbord icoon om het virtuele toetsenbord te openen.[br][/*][*]Klik rechtsboven op het icoon met de drie stippen om de lijst met commando's te openen.[/*][*]Klik op een commando om het in te voeren in het invoerveld.[br]GeoGebra toont meteen ook de verschillende invulsuggesties voor het commando.[/*][/list][size=150]2 INVOERTIPS : [/size][br][list][*]Je moet de invulsuggestie niet wissen of volledig selecteren. Begin je te typen, dan worden de parameters van de invulsuggestie automatisch overschreven.[br][/*][*]Wil je een breuk typen, dan is het niet meer nodig om te starten met een teller tussen haakjes.[br]Typ je eerst het bewerkingsteken voor deling [b]/[/b] of klik je in het virtueel toetsenbord op het bewerkingsteken [math]\div[/math], dan creëert GeoGebra placeholders waarin je vlot teller en noemer kunt invullen zonder haakjes te moeten gebruiken.[/*][/list]
Experimenteer zelf...
repeterende decimale getallen
7/3 noteer je als 2,33... [br]Omgekeerd kan je in GeoGebra ook het repeterende decimaal getal 2,33.. invoeren:[br][list][*]Typ eerst alles wat voor de periode staat: hier 2 en het decimale punt: [b]2.[/b][/*][*]Voer de periode in met een bovenliggend streepje als [math]\bar{3}[/math][b].[/b][/*][/list][u]invoer[/u]:[br]De invoer in het algebravenster toont nu de periode in overline.[br][u]uitvoer[/u]:[br]Mooi is dat je rechts via de blauwe knop achter de uitvoer kunt schakelen tussen breuknotatie of decimale notatie. Je kunt nu naadloos verder rekenen met dergelijke invoer. Het aantal getoonde decimalen in de decimale notatie komt overeen met het aantal decimalen dat je bepaalde als afronding.[br][u]tekst[/u]:[br]Je kunt beide notaties tonen in een tekstbestand met het commando [i]LaTex(getal, true/false)[/i]:[br]- [b]LateX(getal, true)[/b] toont de uitvoer zoals in het algebravenster en wisselt mee met de blauwe knop.[br]- [b]LaTeX(getal, false)[/b] toont steeds de invoer met de periode in overline.[br]Maak je tenslotte een invulvak voor het getal, dan wordt de invoer getoond met de notatie in overline.[br][br]Onderstaande afbeelding illustreert invoer, uitvoer en de notatie in tekst en invulvak.
Experimenteer in het applet met de notatie van decimale getallen
tabelvenster: losse gegevens invoeren
de beschrijvende maten van losse gegevens
[list][*]Open het tabelvenster [img]https://wiki.geogebra.org/uploads/thumb/1/11/TableBlack.svg/24px-TableBlack.svg.png[/img].[/*][*]Typ in de tweede kolom (y_1) een reeks losse gegevens.[/*][*]Klik achter y_1 op de knop [img width=20,height=20]https://lh5.googleusercontent.com/m4JJV-BBHdJBfdjRUsylYIuAaCroguwoVEWij8b4Y7X7OjDbyt-wRNegS8oERyKiujYH5_DaJikRPCfwmR-9Xkls8F0FsM8ibx6wiUkL0Bd4HnBOjYLWKi0JIDWLj7WblgWGdnuM[/img] [i]Meer[/i] en selecteer [b]y_1 Beschrijvende maten[/b].[br]In een dialoogvenster lees je de beschrijvende maten voor de ingevoerde lijst af:[br][i]gemiddelde, standaardafwijking, minimum, Q1, mediaan, Q3 en maximum[/i].[/*][/list]
grafische voorstellingen
[list][*]Open het [img]https://wiki.geogebra.org/uploads/thumb/9/98/AlgebraBlack.svg/24px-AlgebraBlack.svg.png[/img] [i]Algebravenster.[/i][/*][*]Bij het typen van de waarden in kolom y_1 creëert GeoGebra een lijst y_1 als een hulpobject dat, afhankelijk van je instellingen, wel of niet getoond in het algebravenster. Typ je als invoer y_1, dan creëer je een nieuwe lijst l1, die altijd getoond wordt. [br]Je kan dus net zo goed telkens y_1 typen als l1.[/*][*]De eenvoudigste grafische voorstelling van losse gegevens is een dotplot.[br]Je creëert een dotplot van de lijst y_1 met het commando [b]Dotplot(y_1)[/b].[br]In het algebravenster vind je het dotplot terug als een lijst [i]l2[/i] van punten.[/*][*]Je creëert een staafdiagram creëren met het commando [i]Staafdiagram(Lijst gegevens, Breedte van de staven)[/i].[br]Hier wordt dit [b]Staafdiagram(l1, 1)[/b].[br][/*][*]De invoer [b]Boxplot(-2, 1, l1)[/b] creëert een boxplot 2 eenheden onder de x-as met hoogte 1.[/*][/list]Lees de handleiding voor meer uitleg over diagrammen.[br]Klik bovenaan in het virtueel toetsenbord op de drie puntjes en kies rechts de categorie Diagrammen.[br]Verken de verschillende diagrammen die je kunt creëren met GeoGebra en hun syntaxen.
waarden aanduiden op staafdiagram en/of boxplot
De waarden van de beschrijvende maten kun je gebruiken om ze als punten weer te geven op het boxplot en/of het staafgram.[br][list][*][b]Gem = (gemidd(l1), 0)[/b] creëert op de x-as een punt dat het gemiddelde aanduidt.[/*][/list]
frequentietabel
Je hoeft zelf de waarden niet te turven om een frequentietabel met absolute of cumulatieve frequenties op te stellen. Vanuit de lijst l1 met de waarden in de kolom y1 creëer je als tekstobject:[br][list][*]een frequentietabel met de absolute frequenties als: [b]Frequentietabel(l1)[/b],[/*][*]een frequentietabel met de cumulatieve frequenties als [b]Frequentietabel(true, l1)[/b].[/*][/list][u]Opmerking[/u]: Vanuit de waarden in de frequentietabel zou je nu ook een staafdiagram kunnen construeren.Lees de handleiding voor meer uitleg over de mogelijke syntaxen van het commando [url=https://wiki.geogebra.org/nl/Frequentietabel_Commando]Frequentietabel[/url].[br]Samengevat komen die syntaxen hier op neer: [br][list][*]Wil je met cumulatieve waarden werken, dan voeg je vooraan [i]true [/i]toe.[/*][*]Wil je de frequenties uit de lijst herschalen, dan voeg je achteraan twee parameters toe:[br][i]true[/i] en een aanvullende factor waarmee je de waarden in de lijst met frequenties wil vermenigvuldigen. Deze twee vuistregels gelden ook voor histogrammen.[/*][/list]
wat met (grotere) gegevensbestanden?
Hiervoor heb je meerdere mogelijkheden:[br]- In de datatabel kan je csv-bestanden invoeren (zie ook [url=https://www.geogebra.org/m/ermrfpec#material/enxmg3tg]importeren van csv-databestanden[/url]).[br]- In het rekenblad van Suite kan je via knippen en plakken gegevens kopïeren vanuit Excelbestanden.
Punten, lijnstukken, rechten en veelhoeken in de ruimte
Punten lijnstukken en veelhoeken
Selecteer de knop [icon]/images/ggb/toolbar/mode_point.png[/icon] [i]Punt [/i]en klik op het [i]Oxy [/i]grondvlak in het [i]3D tekenvenster[/i]. [br][b]Tip:[/b] Je kunt schakelen tussen horizontaal of verticaal bewegen van een punt door het punt te selecteren. Bij het selecteren verschijnen pijlen naast het punt die de bewegingsrichting aanduiden.[br]Opmerking: Met de knop Punt kan je enkel punten creëren op een bestaand object (het Oxy grondvlak, een eerder gecreëerde rechte, veelhoek of ruimtelichaam). Je kunt ook een punt creëren door als invoer 3D-coördinaten in te geven: De invoer (1, 2, 1) creëert een punt met gegeven x-, y- en z-coördinaat.[br][br]Selecteer de knop [icon]/images/ggb/toolbar/mode_segment.png[/icon] [i]Lijnstuk [/i]en klik tweemaal in het [i]Oxy [/i]grondvlak of op bestaande punten.[br]Je creëert ook een lijnstuk met het commando [b]Lijnstuk( )[/b].[br][list][*][b]Lijnstuk(A, B)[/b] creëert een lijnstuk tussen twee gegeven punten A en B.[/*][*][b]Lijnstuk((1,0,2), (0, 1, 3))[/b] creëert een lijnstuk tussen twee punten met gegeven coördinaten.[/*][/list][br]Selecteer de knop [icon]/images/ggb/toolbar/mode_polygon.png[/icon] Veelhoek, klik op de hoekpunten en sluit de veelhoek door nogmaals het eerste hoekpunt aan te klikken. Analoog als in 2D kan je veelhoeken ook bepalen als bv. [b]Veelhoek(A, B, C, D)[/b].
Rechten
[list][*][i]Twee punten:[/i][br]Selecteer de knop [icon]/images/ggb/toolbar/mode_join.png[/icon] Rechte en klik op twee punten, of definieer een rechte met het commando Rechte(A,B). [/*][*][i]Punt en evenwijdige rechte:[/i][br]Selecteer de knop [icon]/images/ggb/toolbar/mode_parallel.png[/icon] Evenwijdige Rechte, klik op een bestaande rechte en een bestaand punt en creëer de rechte door het punt evenwijdig met de eerste rechte. De volgorde van aanklikken maakt niet uit. Je creëert ook een rechte door het punt A evenwijdig met de rechte a als [b]Rechte(A, a)[/b].[/*][*][i]Punt en richtingsvector:[/i][br]Het commando [b]Rechte(Punt, Richtingsvector)[/b] creëert een rechte door een gegeven punt met gegeven richtingsvector. [br][u]Let op[/u]: Vul voor de richtingsvector geen richtingsgetallen in. GeoGebra interpreteert deze coördinaten als de coördinaten van een gegeven punt. Definieer eerst een vector als bv. u=(1, -1, -1). Door een kleine letter te gebruiken weet GeoGebra dat u een vector is. [br][b]Rechte(A, u)[/b] of [b]Rechte((1, 2, 1), u)[/b] creëert een rechte door het gegeven punt met gegeven richtingsvector.[br][br][/*][/list]
Experimenteer in het 3D venster met punten, lijnstukken, veelhoeken en rechten
Instellingen
Klik op de knop Instellingen in de rechterbovenhoek van het 3D venster en ontdek de mogelijke instellingen.[br][list][*]De assen, het Oxy grondvlak en een raster in dit grondvlak kunnen naar keuze getoond of verborgen worden. Je kunt ook kiezen tussen enkele projectiemethodes.[/*][*]Zo kan je net als in het 2D tekenvenster de assen een label of vaste verdeling geven.[br]Ook kan je desgewenst de 3 assen zwart kleuren ipv rood, groen en blauw.[/*][*]Met clipping bepaal je de grootte van een kubus die vastlegt tot waar objecten getoond worden. Zo lopen rechten niet langer door tot de rand van het 3D venster. [/*][*]De optie belichting geeft ruimtelichamen een extra 3D-effect.[/*][/list]
Werken met matrices
Matrices creëren via het algebravenster
[list][*]In het algebravenster kan je een matrix definiëren als een lijst van rijen. [/*][*]Per rij creëer je een nieuwe lijst met de elementen van de matrix.[/*][*]In het algebra venster wordt de matrix netjes als een mooie matrix getoond.[/*][*]Geef je zelf bij het creëren een matrix geen naam, dan wordt hij automatisch m1, m2,... genoemd.[br][/*][/list]
Matrices creëren via het virtueel toetsenbord
Veel gebruiksvriendelijker om matrices te creëren is het virtueel toetsenbord.[br][list][*]Open het symbolisch toetsenbord.[/*][*]Selecteer de knop matrices op de derde rij..[/*][*]Bepaal in het dialoogvenster de dimensie van de matrix.[/*][*]Gebruik de pijltoetsen op je toetsenbord om te navigeren tussen de placeholders en zo de elementen te bepalen.[/*][/list][u]Opmerkingen[/u]: [br][list][*]Klik je na het creëren van de matrix op het object in het algebravenster, dan verschijnen de elementen opnieuw in placeholders, zodat je eenvoudig individuele elementen kan wijzigen.[/*][*]Analoog kan je met de eerste twee knoppen op derde rij een punt of een vector creëren zonder je druk te maken over haakjes of komma's.[/*][/list]
Rekenen met matrices
Eens je matrices gedefinieerd hebt, kan je vlot met matrices werken als m1 + m1 of m1 * m2.[br]Het element in matrix m1 op rij 1 en kolom 2 vind je als [b]Element(m1, 1, 2)[/b] of als [b]m1(1, 2)[/b].
Matrixcommando's in GeoGebra
Om de determinant van een matrix te berekenen, volstaat het om 'Det' of 'det' te typen in het invoerveld. Na drie letters geeft GeoGebra aanvulsuggesties die je kunt aanklikken of negeren.[br]Een overzicht van alle ingebouwde matrixcommando's vind je als volgt:[br][list][*]Klik op het icoon van het virtuele toetsenbord.[/*][*]Klik rechts op het icoon met de drie puntjes.[/*][*]Selecteer de categorie Vector en matrix voor een overzicht van de commando's.[/*][*]Selecteer je een commando, dan wordt links de juiste syntax getoond.[br]Klik je vervolgens op Toon Online Help, dan wordt je naar een pagina geleid in de Handleiding waarin je meer uitleg vindt over het commando.[/*][/list]
Probeer het zelf...
matrices en breuknotatie
De input {{1 / 2, 2}, {4, 2 / 3}} creëert een 2x2 matrix met twee elementen die geen gehele getallen zijn.[br]In GeoGebra Klassiek6 en Suite verschijnt de breuknotatie in het algebravenster. [br]Via de blauwe knop kan je hierbij schakelen tussen breuknotatie en een decimale notatie. Beide opties blijven ook mogelijk na matrixbewerkingen.[br]Geef je de elementen van een matrix in als kommagetallen en wil je breuken zien verschijnen, wissel dan de app naar CAS, daar worden ze automatisch omgezet naar breuknotatie.[br]Let wel: in Suite worden objecten in de verschillende niet aan elkaar gekoppeld. Wil je in CAS werken, creëer dan ook je matrix in CAS. Meer over matrices in breukvorm lees je in de volgende pagina.
analyse - werken met twee tekenvensters
waarom twee schermen?
Natuurlijk kunnen ook goed gekozen toonvoorbeelden je leerlingen op weg zetten om concepten te begrijpen. Bij het bekijken van het verloop van een veeltermfunctie is het overzichtelijker wanneer de grafieken van een functie f en de bijhorende hellingsfunctie in apart vensters getoond worden.
Een dynamisch punt in twee tekenvensters
Stappenplan
In een toonbestand kan je in een tweede tekenvenster de grafiek van de hellingsfunctie tonen.[br]Tekenvenster 2 open je als volgt:[br][list][*]Open het [b]Menu[/b] door rechtsboven te klikken op de drie horizontale strepen.[/*][*]Selecteer het menu [b]Beeld[/b] en vink tekenvenster 2 aan.[/*][/list]Her verband tussen verloop van f en het teken van f ' illustreer je met een punt op de grafiek van f:[list][*][icon]/images/ggb/toolbar/mode_point.png[/icon]Selecteer de knop [b]Punt[/b] en klik op de grafiek van f in tekenvenster1.[br][/*][*][u]Alternatief[/u]: Typ het commando [b]P = Punt(f)[/b] in het invoerveld.[/*][*][u]Let op[/u]: Wil je nu verder in tekenvenster 2 werken, klik dan eerst in tekenvenster 2 om het te activeren. Nieuwe objecten worden steeds getoond in het actieve venster. Achteraf kan je wel voor elk object in de tab Geavanceerd steeds bepalen in welk(e) venster(s) het wel of niet getoond wordt.[br][/*][*]Definieer in tekenvenster 2 een punt met het commando [b][i](x(P), f'(x(P)))[/i][/b].[/*][/list]Versleep nu in tekenvenster 1 P op de grafiek van f, zie hoe het punt op de grafiek van f' mee beweegt en leer waarom men f ' ook de hellingsfunctie van f noemt.
Probeer het zelf...
GeoGebra in toetsen en examens
De examenmodus
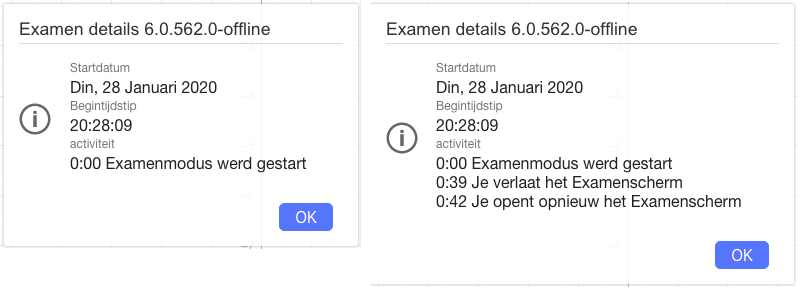
De GeoGebra examenmodus werd gecreëerd om GeoGebra als grafische rekenmachine te gebruiken tijdens schriftelijke toetsen en examens. [br][br]De GeoGebra examenmodus ...[br][list][*]is bereikbaar op [url=https://www.geogebra.org/]GeoGebra wiskunde apps[/url].[br][/*][*]werkt op je mobiel toestel zonder bijkomende installaties.[br][/*][*]werkt in volledige schermgrootte zodat er op het scherm geen ruimte meer overblijft voor andere informatie.[br][/*][*]laat geen toegang toe tot het internet, de GeoGebra website, of bestanden opgeslagen op je computer of mobiel toestel.[br][/*][*]zet de apps vast op je mobiel toestel.[br][/*][*]toont een duidelijke waarschuwing van zodra de Examenmodus zonder toelating verlaten werd.[/*][/list][br]Na het afsluiten van de examenmodus wordt een afbeelding gecreëerd van de examendetails. Deze afbeelding kan je bezorgen aan je leerkracht.
Initiatiehandleiding
De examenmodus kan niet alleen individueel opgestart worden door alle leerlingen apart, maar ook gecentraliseerd door de leerkracht via specifieke toestelapps: Apple Classroom, Google Scenes, Jamf, Google Manager, Kiosk Modus op Chromebooks...[br]Raadpleeg hiervoor de ict-verantwoordelijken op de school.[br]Je leert meer over het gebruik van de examenmodus in de [url=https://www.geogebra.org/m/scntsjc9]initiatiehandleiding GeoGebra voor toetsen[/url] op de GeoGebra openingspagina.
aanvinkvakjes
aanvinkvakjes
Algebraïsch zijn aanvinkvakjes Booleaanse variabelen met [i]true [/i]of [i]false [/i]als mogelijke waarde.[br]In het tekenvenster kan je ze tonen als aanvinkvakjes die je kan selecteren of deselecteren.[br]Je kunt ze gebruiken om een of meerdere objecten te tonen of te verbergen. Objecten kan je ook tonen of verbergen door in het algebravenster vooraan in het invoerveld van het object op de bijhorende bol te klikken. Bestaat je constructie uit heel wat objecten en wil je met één klik meerdere objecten tonen of verbergen, dan zijn aanvinkvakjes erg interessant.[br][list][*]Klik in het knoppenvenster eerst onderaan de optie [i]MEER[/i], selecteer in de categorie [i]Andere [/i]de knop [b]Aanvinkvakje [/b]en klik in het tekenvenster. [/*][*]In een dialoogvenster kan je nu je aanvinkvakje een titel geven en bestaande objecten linken al hoeft dat niet meteen.[/*][/list]
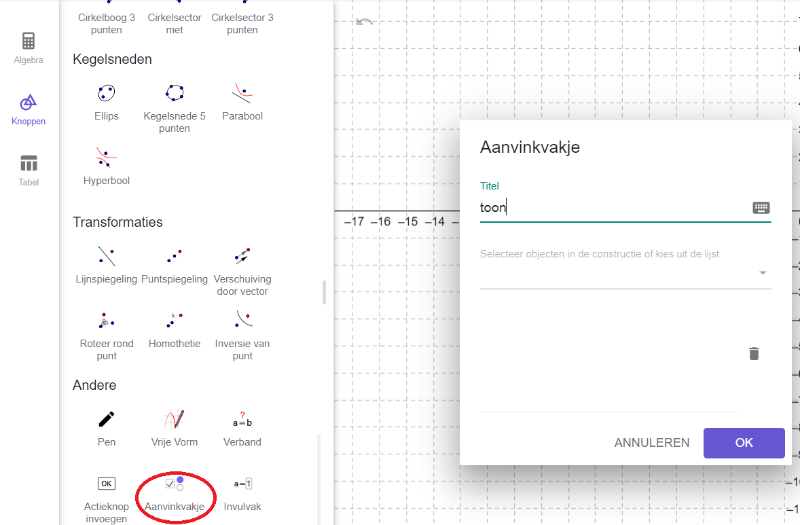
aanvinkvakjes
Om het even wanneer kan je steeds een object linken aan een aanvinkvakje. Zo bepaalt een punt [i]BC[/i] op de goniometrische cirkel de complementaire hoek van de gegeven hoek. Je wil het punt dan ook enkel tonen als het [i]aanvinkvakje a[/i] geselecteerd is.[br][list][*]Open de [i]Instellingen [/i]van het punt BC en typ [b][i]a[/i][/b] in de tab Geavanceerd als voorwaarde om BC te tonen.[br]Naast het punt BC kan je ook bijkomende hulplijntjes en de complementaire hoek zelf linken aan hetzelfde aanvinkvakje a en hoef je niet al deze objecten apart aan of uit te vinken.[/*][/list]
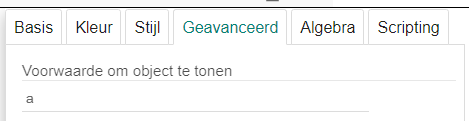
exclusief selecteerbare aanvinkvakjes
Wil je telkens slechts één verwante hoek tonen van een gegeven hoek, dan kan je met een eenvoudig script de aanvinkvakjes exclusief selecteerbaar maken.[br]Na selectie van een verwante hoek, kan je wel of niet hulplijntjes naar de assen tonen.
scripting
[list][*][b]a, b, c en d[/b] zijn aanvinkvakjes voor respectievelijk de complementaire, supplementaire, antisupplementaire en tegengestelde hoek. [b]g[/b] is een aanvinkvakje om hulplijntjes te tonen van de punten op de geoniometrische cirkel naar de assen.[/*][*]Bij het selecteren van een verwante hoek worden de overige aanvinkvakjes gedeselecteerd.[br]Telkens worden ook de hulplijntjes naar de assen verborgen.[br]Voor het aanvinkvakje a typ je in de tab Scripting volgende commando's:[br][b]Als(a, SetValue(b, false))[br]Als(a, SetValue(c, false))[br]Als(a, SetValue(d, false))[br][/b][b]Als(a, SetValue(g, false))[/b][br]Voor de aanvinkvakjes b, c en d typ je analoge commando's.[/*][*]Voor het aanvinkvakje g typ je in de tab Geavanceerd als voorwaarde om te tonen [b]a [/b][b]∨ b [/b][b]∨ c [/b][b]∨ d[/b].[br]het aanvinkvakje g wordt dus slechts getoond als a of b of c of d geselecteerd is.[br][u]Opmerking[/u]: de OF-operator kan je ook invoeren als 2 verticale streepjes: ||. [br]GeoGebra wijzigt deze invoer automatisch in het OF-symbool.[/*][*]Je kunt ook vermijden dat geen van de opties geselecteerd is, bijvoorbeeld: als b, c en d niet geselecteerd zijn, dan wordt automatisch a wel geselecteerd. [br]Plaats hiervoor in de tab scripting van de aanvinkvakjes a, b, c en d volgend commando: [br][b]Als(!b && !c && !d, SetValue(a, true))[/b].[br][i](Als niet b én niet c én niet d, geef a dan true als waarde.)[/i][/*][/list]