Triângulo
Um triângulo é uma figura geométrica plana com três lados, três ângulos e três vértices. A soma dos seus ângulos internos é sempre 180°, e eles podem ser classificados tanto pela medida de seus lados (equilátero, isósceles, escaleno) quanto pela medida de seus ângulos (acutângulo, retângulo, obtusângulo).
Inhoudstafel
- Triângulos
- Triângulo
- CONGRUENCIA DE TRIANGULOS
- Triângulos e Cálculo da Área de Triângulos.
- Exercícios do capítulo 4
- Exercícios do capítulo 10
- Atividade sobre Triângulos
- Classificação de Triângulos
- atividade de congruência de triângulos
Triângulo
Definição
Três pontos não colineares formam um triângulo. Nesse caso, a região triangular correspondente é a região limitada do plano, delimitada pelos segmentos que unem os três pontos dois a dois. [br]Sendo A, B e C tais pontos, então A, B e C são os vértices do triângulo ABC.
Um triângulo ABC é denominado:
a) Equilátero, se [math]AB=AC=BC[/math].[br][br]b) Isósceles, se ao menos dois entre [math]AB,AC,BC[/math]forem iguais.[br][br]c) Escaleno, se [math]AB\ne AC\ne BC\ne AB[/math].
Problema 1
Construa um triângulo a partir de três segmentos dados.
Solução
[list=1][*]Trace uma reta r e, sobre ela, marque os pontos B e C tais que [math]BC=a[/math].[/*][*]Trace os círculos de centro B e raio c e de centro em C e raio b. [/*][*]Marque o ponto A como um dos pontos de intersecção dos círculos traçados. [/*][*]Trace os segmentos AB, AC e BC, formando o triângulo ABC. Note que [math]AB=c,AC=b[/math] e [math]BC=a[/math].[/*][/list]
Triângulo a partir de três segmentos
Problema 2
Construa um triângulo dados dois lados e um ângulo.
Solução
Primeiramente vamos transportar o ângulo, e na sequência, traçaremos o triângulo. [list=1][list=1][*]Trace um círculo de raio arbitrário [i]R[/i], centrado no vértice [i]A[/i] do ângulo dado, marcando os pontos [i]X [/i]e[i] Y[/i] sobre as intersecções do círculo com os lados do ângulo. [/*][*]Marque o ponto [math]A_1[/math] no plano e trace a semirreta com origem e[math]A_1[/math].[/*][*]Trace um círculo de raio [i]R[/i], com centro em [math]A_1[/math] e marque [math]X_1[/math]x no ponto de intersecção do círculo com a reta [i]r[/i]. [/*][*]Agora trace outro círculo de raio igual ao segmento [i]XY[/i], com centro em [math]X_1[/math] e marque o ponto [math]Y_1[/math] na intersecção dos dois círculos. [/*][*]Trace a semirreta [math]A_1Y_1[/math]. [/*][*]Trace dois círculos, um com centro em [math]A_1[/math] e raio [i]b[/i] e outro com centro em [math]B[/math] e raio [i]a[/i]. [/*][*]Marque o ponto [math]C[/math] de intersecção dos dois círculos. [/*][*]Traçando os segmentos [math]AB=b[/math], [math]BC=a[/math] e [math]AC[/math], formamos o triângulo[i] ABC[/i] de ângulo [math]BÂC=\beta[/math]. [/*][/list][/list]
Triângulo a partir de dois lados e um ângulo
Problema 3
Construa um triângulo dados um lado e dois ângulos.
Solução
[list=1][*]Trace uma reta [math]t[/math] e sobre ela marque o segmento [math]AB=c[/math]. [/*][*]Transporte os ângulos [math]\alpha[/math] para o vértice em A e [math]\beta[/math] para vértice em B. [/*][*]Trace as semirretas [math]AY_1[/math] e [math]BN_1[/math]. [/*][*]Marque o ponto [math]C[/math] de intersecção das duas semirretas. [/*][*]Traçando os segmentos [math]AB=c[/math], [math]BC[/math] e [math]AC[/math], formamos o triângulo [math]ABC[/math] de ângulo. [/*][/list]
Triângulo a partir de um lado e dois ângulos
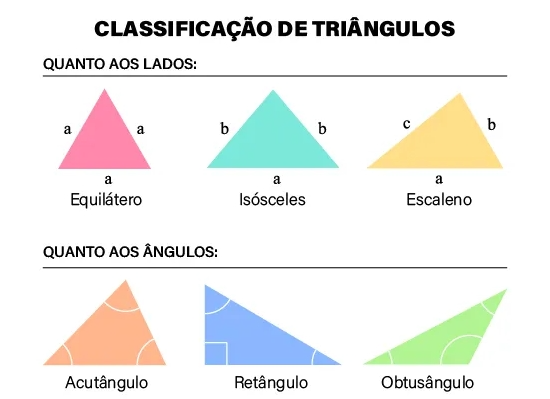
Classificação de Triângulos
Prezado(a) estudante, é um prazer tê-lo aqui! Fico feliz que você está trilhando uma jornada rumo ao conhecimento. [br][br]Espero que essa atividade possa te ajudar no aprendizado à respeito da [b]Classificação de Triângulos[/b] quanto às medidas dos [b]lados[/b] e [b]ângulos[/b]. [br]Vamos juntos?[br][br]Lembre-se: [color=#ff0000]"Estudar é investir no seu futuro."[/color]
Você sabia que os triângulos são classificados de acordo com seus lados e seus ângulos? Para cada tipo de triângulo há um nome específico. Vamos conhecê-los?
Para iniciar, assista ao vídeo abaixo: ↓
Triângulos e suas classificações
Mais um vídeo para você assistir e ficar [b]FERA[/b] no conteúdo! Vamos lá?
CLASSIFICAÇÃO dos TRIÂNGULOS quanto às medidas dos LADOS e ÂNGULOS
Agora, responda as seguintes questões para fixar os aprendizados obtidos: ↓
Questão 01.
Com base nos vídeos assistidos, descreva quais são as [b]classificações de cada triângulo em relação à medida dos seus [color=#ff0000]lados[/color][/b] e a sua principal [b]característica[/b].
Questão 02.
Por fim, descreva quais são as [b]classificações de cada triângulo em relação à medida dos seus [color=#ff0000]ângulos[/color][/b] e a sua principal [b]característica[/b].
Separei uma imagem para solidificar o conteúdo, confere aqui embaixo! [br][br][b]Dica:[/b] Tente identificar as características de cada triângulo (conforme estudado acima) na imagem abaixo.
Agora, fica aqui uma inspiração de mapa mental caso queira reproduzir. Topa?
O que acha de fazer alguns exercícios para colocar em prática o que aprendeu? Segue o PDF com algumas questões para você responder, ok?
Atividade - Classificação de Triângulos
Mais duas questões abertas... Aguenta aí que estamos chegando ao fim!
Questão 03.
Escreva ([b]respectivamente[/b]) como são classificados os triângulos que possuem: [br] – todos os lados iguais;[br] – dois lados iguais;[br] – todos os lados diferentes.
Questão 04.
Agora, escreva ([b]respectivamente[/b]) como são classificados os triângulos que possuem: [br] – ângulos agudos (menores que 90°);[br] – um ângulo reto (mede 90°);[br] – um ângulo obtusângulo (maior que 90°) e dois agudos.
O que acha de interagir um pouco? Dá só uma olhada no que preparei para você! ↓[br][br][b]Como funciona:[/b] [br]– Mova o controle deslizante e observe o ângulo mudar.
Classificação de Triângulos quanto aos ângulos ↓
Percebeu que o triângulo muda conforme o valor do ângulo é alterado? ↑[br]Agora, pergunte-se: [br] – Como é classificado o triângulo formado quando o valor do ângulo é de [color=#ff0000]60°[/color]?[br] – E, o triângulo formado quando o ângulo é [color=#ff0000]90°[/color]?[br] – Por fim, como classificamos o triângulo formado quando o ângulo corresponde a [color=#ff0000]120°[/color]?
Mais um pouquinho de interação... ↓[br][br][b]Como funciona:[/b] [br]– Mova os controles deslizantes e observe o triângulo mudar.
Classificação de Triângulos quanto aos lados ↓
Perceba que os lados do triângulo mudam conforme a interação com os controles deslizantes. ↑[br]Após a interação, se pergunte: [br] – Como é classificado o triângulo formado quando os [color=#ff0000]três[/color] controles deslizantes estão posicionados no [color=#ff0000]mesmo valor[/color]?[br] – E, o triângulo formado quando apenas [color=#ff0000]dois[/color] controles deslizantes estão posicionados no [color=#ff0000]mesmo valor[/color]?[br] – Para finalizar, como classificamos o triângulo formado quando os [color=#ff0000]três[/color] controles deslizantes estão posicionados em [color=#ff0000]valores distintos[/color]?
Vamos finalizar com algumas perguntas objetivas, ok?[br][br]Leia com [b]atenção[/b] e marque apenas [b]uma alternativa[/b] em cada questão. ↓[br]Estou orgulhosa de você por chegar até aqui!
Questão 01.
Um triângulo que possui [b]todos os lados com a mesma medida[/b] é conhecido como um triângulo:
Questão 02.
Observe o triângulo a seguir e responda. [br][br][img]https://s2.static.brasilescola.uol.com.br/exercicios/2024/09/1-questao-nove-classificacao-triangulos.jpg[/img][br][br]Esse triângulo pode ser classificado como:
Questão 03.
Uma reserva florestal possui formato triangular com lados medindo 9 km, 11 km e 7 km. Podemos afirmar que essa reserva possui formato de um triângulo:
Questão 04.
Dois triângulos observados apresentam as seguintes características: o primeiro possui um ângulo de 90° e o segundo possui dois ângulos internos iguais a 45°. Esses triângulos são [b]respectivamente[/b]:
[b]Parabéns![/b] Você chegou até o fim da nossa atividade sobre Classificação de Triângulos![br]Estou muito feliz, querido(a) aluno(a)! [br][br]Continue estudando e se dedicando. Seu futuro será brilhante! [br]Abraços.
