Dissecting a cube into equal parts

Diego Lieban, Dec 9, 2018

The aim of this book is sharing some possibilities to split a cube into equal parts, i.e., with the same area and the same volume. The arose question here is: for which natural values of n is that possible? We are not considering in this questions the cases which the cube is divided by parallel plans.

Table of Contents

  1. by 2
    1. Mitad del cubo (3)
    2. Sección modular 7. Rombos y trapecios
    3. Mitad del cubo (7)
    4. Mitad del cubo. Simetría
    5. Screwed Bisection of a Cube
    6. Screw Bisection of a Cube
    7. Dividing a cube by 2
    8. Dividing a cube by 2
    9. cube divided into 2 equal parts by Rinus Roelofs
    10. Mitad del cubo (8)
    11. Half of a cube with ruled surfaces
    12. cube divided by 2
    13. cube divided by 2 (workshop Český Krumlov)
    14. examples to inspire cube dissection
    15. Sección modular 3. Triángulos
    16. Sección modular 4. Trapecios
    17. Sección modular 1
    18. Mitad del cubo (10)
  2. by 3
    1. Dividing a cube by 3
    2. Cube Volume
    3. Cube Dissection
    4. 1/3 cube
  3. by 4
    1. Dividing a cube by 4
    2. Overlapping Quarters of a Cube
    3. quarters of a cube
    4. Recursive Solution
    5. dissecting a cube into 4 equal parts
    6. Divisão do cubo
    7. Dividindo cubo em partes iguais
  4. by 5
    1. MMC exemplo2
  5. by 6
    1. Dividing a cube by 6
    2. opening a cube
  6. by 7
    1. Dividing a cube by 7
  7. by 8
    1. 1/8 cube
  8. by 9
    1. Dividing a cube by 9
    2. cubo Mari
  9. by 12
    1. 12-Lizard

1.

by 2

  • 1. Mitad del cubo (3)
  • 2. Sección modular 7. Rombos y trapecios
  • 3. Mitad del cubo (7)
  • 4. Mitad del cubo. Simetría
  • 5. Screwed Bisection of a Cube
  • 6. Screw Bisection of a Cube
  • 7. Dividing a cube by 2
  • 8. Dividing a cube by 2
  • 9. cube divided into 2 equal parts by Rinus Roelofs
  • 10. Mitad del cubo (8)
  • 11. Half of a cube with ruled surfaces
  • 12. cube divided by 2
  • 13. cube divided by 2 (workshop Český Krumlov)
  • 14. examples to inspire cube dissection
  • 15. Sección modular 3. Triángulos
  • 16. Sección modular 4. Trapecios
  • 17. Sección modular 1
  • 18. Mitad del cubo (10)

1.1.

Mitad del cubo (3)

De aspecto similar a mitad del cubo (2), en este caso los hexágonos que se forman tienen lados paralelos de distinta longitud, excepto para t=1/2 que también se obtiene un hexágono regular.[br]
– Jose Manuel Arranz

1.2.

–

1.3.

–

1.4.

–

1.5.

–

1.6.

–

1.7.

–

1.8.

–

1.9.

–

1.10.

–

1.11.

–

1.12.

–

1.13.

–

1.14.

–

1.15.

–

1.16.

–

1.17.

–

1.18.

–

2.

by 3

  • 1. Dividing a cube by 3
  • 2. Cube Volume
  • 3. Cube Dissection
  • 4. 1/3 cube

2.1.

Dividing a cube by 3

– Diego Lieban

2.2.

–

2.3.

–

2.4.

–

3.

by 4

  • 1. Dividing a cube by 4
  • 2. Overlapping Quarters of a Cube
  • 3. quarters of a cube
  • 4. Recursive Solution
  • 5. dissecting a cube into 4 equal parts
  • 6. Divisão do cubo
  • 7. Dividindo cubo em partes iguais

3.1.

Dividing a cube by 4

– Diego Lieban

3.2.

–

3.3.

–

3.4.

–

3.5.

–

3.6.

–

3.7.

–

4.

by 5

  • 1. MMC exemplo2

4.1.

MMC exemplo2

– Diego Lieban

5.

by 6

  • 1. Dividing a cube by 6
  • 2. opening a cube

5.1.

Dividing a cube by 6

– Diego Lieban

5.2.

–

6.

by 7

  • 1. Dividing a cube by 7

6.1.

Dividing a cube by 7

[math]\frac{1}{7}+\left(\frac{1}{7}\right)^2+\left(\frac{1}{7}\right)^3+\left(\frac{1}{7}\right)^4+\left(\frac{1}{7}\right)^5+...=[/math]
Think how can you divide a cube into 7 equal parts, all of them with the same volume and surface as well.
– Diego Lieban

7.

by 8

  • 1. 1/8 cube

7.1.

1/8 cube

this version is able to download as STL
this version is NOT able to download as STL
Adapted from [url=http://gallery.bridgesmathart.org/exhibitions/2018-bridges-conference/shen-guan-shih]http://gallery.bridgesmathart.org/exhibitions/2018-bridges-conference/shen-guan-shih[/url].
– Diego Lieban

8.

by 9

  • 1. Dividing a cube by 9
  • 2. cubo Mari

8.1.

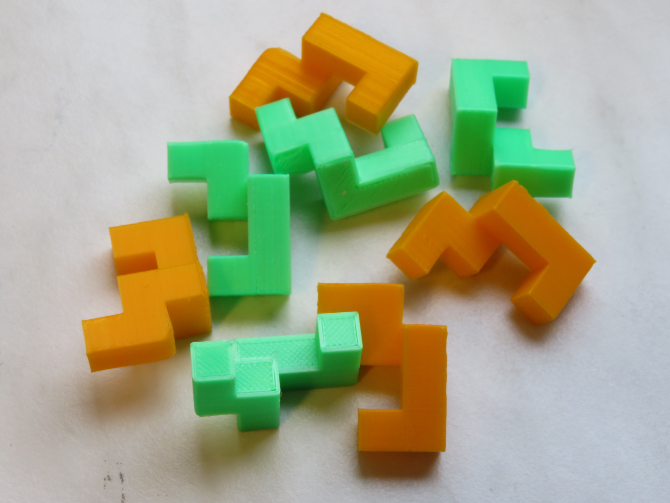
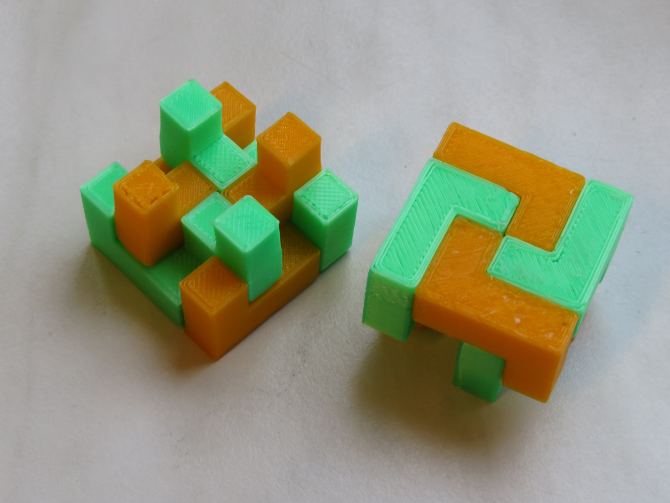
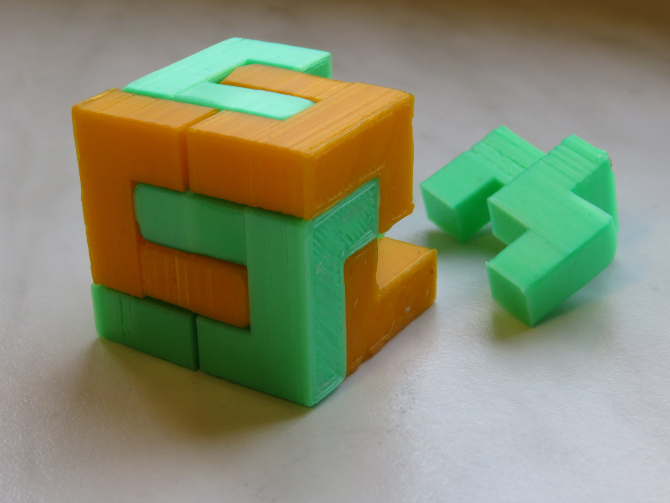
Dividing a cube by 9

reference: [url=https://www.quora.com/How-would-you-cut-a-cube-into-9-pieces-with-equal-volume-and-equal-surface-area]https://www.quora.com/How-would-you-cut-a-cube-into-9-pieces-with-equal-volume-and-equal-surface-area[/url]
– Diego Lieban

8.2.

–

9.

by 12

  • 1. 12-Lizard

9.1.

12-Lizard

Inspirado no livro [url=https://www.amazon.com.br/Mind-Blowing-Paper-Puzzles-Ebook-Interlocking-ebook/dp/B07NQSLQBX]Mind-Blowing Paper Puzzles[/url], de Haruki Nakamura.
– Diego Lieban

Information