
Arc Length and Sector Area
Check this out.
[size=150][b]Use the applet below to explore how changing the central angle affects the sector area and arc length of a circle.[/b][/size][br][size=85]以下のアプレットを使用して、中心角の変更が円の扇形領域と円弧の長さにどのような影響を与えるかを調べてください。[/size][br][br][b][size=150]Observe and record how changing the central angle affects the size of the sector and the length of the arc[/size][/b].[br][size=85]中心角の変化が扇形のサイズと円弧の長さにどのような影響を与えるかを観察して記録します。[/size][br][br][size=150][b]a.45[/b][math]^\circ[/math][b], 90[/b][math]^\circ[/math][b], and 180[/b][math]^\circ[/math][b][br]b. 30[/b][math]^\circ[/math][b], and 90[/b][math]^\circ[/math][b][br][/b][/size][br][size=100][b][color=#0000ff]Note: You have 5 minutes to complete the following questions below.[/color][/b][/size][br][size=85]5 分以内に以下の質問に答えてください。[/size]
QUESTION 1
[b][size=150]What happens when you double the central angle?[br][/size][/b][size=85]中心角を2倍にするとどうなるでしょうか?[/size]
QUESTION 2
[size=150][b]Two sectors are created from the same circle. [br]The central angle of the first sector is 30°, and the central angle of the second sector is 90°. [br][br]Which of the following best describes the relationship between the central angle, arc length, and sector area in a circle?[/b][/size][color=rgba(0, 0, 0, 0.87)][br][/color][size=85]円の中心角、円弧長、扇形面積の関係を最もよく説明しているのは次のうちどれですか?[/size]
QUESTION 3
[size=150][b]Doubling the central angle doubles the arc length and the sector area.[/b][/size][br]中心角を 2 倍にすると、円弧の長さと扇形の面積も 2 倍になります。
QUESTION 4
[size=150][b]The arc length and the area of sectors made from the same circle are [color=#ff0000]not proportional[/color] to the measure of the central angles.[/b][/size][br][size=85]同じ円から作られる弧の長さと扇形の面積は、中心角の大きさに比例しません。[/size]
Let's Solve
[img]https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTn1YON6eloOxeYQzikjnIk6p4i8xXnQRnUcQ&s[/img]
Formula for solving the arc length and area of a sector.

PRACTICE 1
[b]Given a sector with a radius r= 3m, and a 90°central angle, what is the arc length and sector area?[/b]
PRACTICE 2
[b]Given a sector with a radius r= 3m, and a 120°central angle, what is the arc length and sector area?[/b]
Visualize
Watch this.
[img]data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEAAkGBxITEhUTEhMVFhUVGR0YGBgXGRcaGhoaHhgYGBgYHRkdHigiGBolHx4XITIhJSkrLi4uFx8zODMtNygtLisBCgoKDg0OGhAQGy8lHyUtLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLf/AABEIAMMBAwMBEQACEQEDEQH/xAAcAAACAgMBAQAAAAAAAAAAAAAABQQGAQMHAgj/xABMEAACAQIEAgcDBwgIBQMFAAABAgMAEQQSITEFQQYTIlFhcYEykaEHI0JSsbLRFDNicoKSosEkQ1NzwtLh8BUWNJPxY6O0RFR0g7P/xAAaAQEAAgMBAAAAAAAAAAAAAAAAAwQBAgUG/8QANREAAgIBAwIDBQcEAwEBAAAAAAECAxEEITESQQUyURMiYXGhFEJSgZGx0SMzwfAGFeHxYv/aAAwDAQACEQMRAD8A7jQBQBQBQBQBQBQBQBQBQBQBQBQBQBQBQBQGCaAiTcQQbdo+H41o5pE0KJSIcvEXO1h8ajdjLEdNFckZ5mO7H31q2+5Kq4LhGtm76KLfCMynCC3aQLibbNbyNbquz0K8tTpu8kTMNxW2jEEel/8AWtl1rlEEnp5eSa/UbxyBgCDcGpCI9UAUAUAUAUAUAUAUAUAUAUAUAUAUAUB4klUbkDzrDaRlRb4I0nEoxz+BrCkm8IzKDguqWyIOI48B7Ck+J0qzGhvk5tmvivKs/QitxmaxbsKo3J0A9SbVHbOiraUt/Tv9DWF2pt8kRPivlCw0Xt4qEnujVpPigI+NQe26vJXJ/PCLUYX/AHpRX1I4+VvBDfrG/VjI+81aN3viC/X/AMLEUu7+huh+Vnh53Mi+aN/hBrXq1C5gv1NsR9R9wzpngZyBHiIyx2Umzfumx+FHqenzxa+v7Gej0HqyA7EVLC2E1mLya4ZExHEVGi9o/CjsSJoaeUt3sLpsQzbn05VE5NlyFUY8GqtTd7GmTEgeJqxXppy52OdqPE6qtlu/h/JGfEMfDyq5DTQj8Ti3+J32cPC+BqJqdLHBQcnLlhWTAUBtgndfYYjy/CopOvu0SwnbHy5G+D40dpV/aA+0fhUEow+7JfqjoU6ufFifzwOkcEAg3BqIvp5PVDIUAUAUAUAUAUAUAUAUAUBqxGIVBcn051hySN4QlN4Qrnx7Nt2R8ffULsb4LcNMlzuQ3bma1inJ4RLZONUHJ7JEFmLn7BXSxDTw6pM8nffbq7Mfoil9JOnscJMeFCyyDQyNrGp7lA/OHx286pSnbf8A/mPp3f59i9To4V7y3f0OecU4tPiGzTyvIeQY9keSjsr6AVvXTCHlRbbyQ6kMBWQFAYIoBzwfpRjMNYRTNl+o/bTyyt7I/VtVezTVz3a3+GzN1OSL9wL5TIXsuKTqW+ul2jPmPaT+LzqvKi2Hl95fUsw1PqXNcYrKHQh0bUOpBU+TC9SUKNrx1Yfo+SHU+Iey4g3+xokmJ8vCunXRCBwtRr7rtm8L0RrqYontIidgfPl76gt1NVfmlj/fQmross8qYn4j0mwUFxJiEZh9GL5xr9xy6KfMiqz1rl/ag38Xsv5LkPDpffkl9SuY35SoxpBhmb9KV7fwJf71aN6mfMkvkv8ALLUNFRHtn5sR4r5Qsc3sNFF/dxrf3vmrT7Mpedt/N/xgsRhCPlil+Qvl6XY9t8XN6Nl+7an2WlfdRv1M0p0lxoNxi8R6yyH4E1n7LS/ur9B1S9RngPlB4lEbjEZx9WRVI94Ab41q9HV93K+TZnrZfejXyuRuQmLTqidM6klPXmnrcd5FaON1fD6l+j/9Huv4HTcPOrqGUggi4I1BHKpa7IzWUYaaNtSGAoAoAoAoAoAoAoDRi8QEF+fIVrKWEb1wc3hCSSQsbk3NV22+TpQgorCPNDYj41tAO+rekjmTfocbxmzFagu7Oe/KN0jMY/I4WszAGdhuARcRDuuLFvAgczUPV9os635U/d+Px/gh01PsYf8A6fP8HN6sk5Mx3DmiCXZGZ1VsiEl1zokiBlsN1dSCtxuL3BFYyDVjsG0UjRvbMhytY3Aa2q3GmYG4Pip7qZBn8jbquuGUqGCNYjMpIJXMu4VrNY7dgiiBGVgdjWQesp7vD17qxkGKyD3NCyHKwIItcHfUAj4EUBJ4XxafDtmgleMnfKdD+sp7LeoNR2VQs8yyZTwWjDfKTih+cigk8crIfXK1vhUapnHyWSX1/cjdVUuYoxiflIxR/NxwR+OVnI/eYj4UdEpeecn+eP2Eaao+WKK3xTjWJxH5+aSQfVJ7P7gso91bworh5USZZAqUwFAFAFAFAFAFAdB+Sjpc8Ey4WVrwyGyX+g52A/RY6W+sR3mqeoh7N+2j+fxX/hvF52Z3RTep001lGpmsgKAKAKAKAKAKAR4+XM57hoP51BN5Z0KIdMSPWhOFAR8SQLM3srdj5AZj9lbOxwpnjl4X6vBytfV121Z4y/5PnvG4tppHlf2pGLnzJvbyG1WYRUIqK7GreXk0GtzA9xfH8/5G5VS2HsWVY4owckhMYBVQbZAq22GUab1qDdw/j64XEzyRXmSRtCxZBlL9ZmK20mGgV/oNmIzXFMAXRYtFw7qCS8k6MQdxHErkEtzLNIf+2drigNnHuNHElSUy5ARrJI51tp2jZRpsAKygbOCceOHjljCFhLcMc5UqMjpmj0skna1fW6jLaxJo0Bc+MYxdVliC94iiD73/ADmXP/FtpTAPXFMX1sryWy5ze1720A3ogRayAoAoDfgZI1cGVSyWYFQQDqjKpBOxDEG/hWGAx8yO5aNMikLZd7EIobXmM2Y38aIGigJ3BcZHFLnkTOLEAdx0192ZfDNcagUBGxbIXcxrlTMcg10W/ZGpJva3M0BqrICgCgAOV7SmxGoPcRqDWGs7MZwfVXB5+shjf6yBveL1U0r/AKS+GV+jN58kyrBqFAFAFAFAFAFAVwmqrOtHhGKGQoCLxWPNBMBuYpAPWNhUN79z81+6Ibopxz6HzstdQ5pmgCgCgHeE4ZA2Gll675xIc3Va5hJ16Rkk2y9XkZLa3JkP1TWoI/EsNh1jQxSZnNsw6xn0y3Ohw0YWx0tnb+dZBt6NYfCuzjFtkTs5WDlWzZwMtgrdgi+ZrdkC9+RAhBYMr5jIJbnKqKjR+F3L3I8QPfQHriuS8fV5bdTFfLzcxqZL/pZiwPlRAhVkBQGKAZmBYFDSqGmIukTbICLq8o5k6ER89C2nZbANnFuISCaQAqRmNrpEf8AHuAogQjjnPKP/ALUP+SmAN8Nh42hYzRr1rxPJFlGTKqAkSMFsDmIsotsCea1gFfrYBQBQBQHqGEuyovtOQq+bGw+JrWUulNvsZwfVfDYckSINlUD3VV0qxUs/P9TafmJNWDUKAKAKAKAKAKAr+ISzMPGqsludOqWYJmuhIFAa8VIqo7ObKqsWJ5AKST7qg1Hkx3yv3NLH7rPm9BoPKuqco9UAUAUA0SHEjCtlitA5DvKB7WVsioXvYAPr1ehuQSCALYBE/wCHzdV13VSdVt1mRsm+X27W30330pkGqHDu5UIpYswQWG7toq/rHWw8DWcgzHhmZZGA0iCl9RcZmCLp+sbVjICbDFVjY2tIpZe+wdozfu7St7qA1VkDLg4wxWUTkBso6onrSA2t/wA3z29oW0rDBs4IqKkuIe+aIxrH2VcB5OsIcqWAbKIzYHS5BN7WJghusTEkzSEtclnjBJJ1JJ6xiSTuaAl8Yw69c95kubHtCe+qg69hvtogecDw9LtJIyPFEudwjdphmVFQD2lzOyKWtoCTuLUBKw/WGaZpcmeTDSv2GjYBTAWSwRjlUJlyryXLyrAEVbAKAKAKAuvyTcDOIxokI+bgGYnlnNwg9O037I76qap9SVa5l+3c3htufQAFTJYNTNZAUAUAUAUAUAUAm4n+cPkL/wC/dUFnJf03kIlaFg0Y3GRwoZJnWNBuzGw8h3nwGtRStWelbv0RpKaitzlXTfp0cSpgw4Kwn2mOjSW5W+inO250vbUGanTy6uuznsvT+WUbbnPZcFJq6QBQBQBQE9eLSCA4aydUTmtlF+svfrc2/WW7F9smlqxgGhcawTqwsVjoW6qHrCL3t1uTP/FTAH3Q+SeGVJAAsedHbMqsewTYoG9l8rOoYbCRqr2amuG2f0LtOgut3SwviSsKmJjjkiTFsiS6lU6wBTnDkqQwsTbKe8EioPtsfQuLwiX4hPj+GTZY1GVliUquW97GR5NQed3bblapI62t87EVnhVsVmLTE5FtDVuLUllHNnCUHiSwwrJqMsL/ANHiP77Dj+DFmsMEfC8PeRJHXLaMXYE2YizMSBzsqsT5UyDPFrdabW9lDpbnGh5ACiBv4YR1GM/uo/8A5WHoDZw3GvIzB3JCYWdFF9FVcLIAANhoB571gCmtgFAFAYJoDu/QzDfkGHSLKC5GeXvLtYkX/RFl/ZqHTVe1zc++y+SKeo1jqs6Etlz8y6YLiKSbGx7jv/rUsoOPJNVqIWcPcmVoThQBQBQBQBQEfF4oIO88hWspYJK63NiHE4hVDSSMFUaszEAAd5J2qnO1L4v07nQ92Cwc/wCkfylopKYJQ55yyA5f2U0LeZsPA1mOnss3m8L0XP6lWzU9olD4tJi50XFYgyOjsUSRrZcwFyqqNF2OwA0PcauV1Qr2iis5N8iupTUKAKAKAKAKA24aO7AWJ12G9V9RZ0Q25L2g0/trVnhblwiUAADT3/zrinqMnugCgFnGsEGXMB2h3cxU9F0q38CvqdLC+Di+ezK0RXZjJSWUeUsrlXJxksMZQf8ARzeOIgH/ALWLrLNDxgnKRuWZljk7JRSA0uUjsg2JVRfVra6rrc2w2luZMScVmJvdBrsI4tALlQLqdBtudAByqrPUrHulmGnefeMR8ZxCq6LKQrgKwCqLgZbDa49kbHlUT1Ms7EvsIYMxcanyyKXLdYpS7MbKrG8hA2uwLLtoGa2pvUi1XqRvTejIF9bc+6rUJqSyivKDi9zNbmgUBsw0oV1Yi4VgxHfYg2rWabi0jK5O9mZZLSIcySDOrDYqdRW+hmnSo91s/mcTWQcbm333MA1bKqeNxzw/jJFlk1H1uY8++oJ094nRo1uPds/UfKwIuNRVY6aae6M0MhQBQC/GY+2i79/IfjUcp42RYqoct5cFY6R9IIsJH1sxJLaIg9p27h3AczsPcKqSlOcumHPd+hZnONawjjHSPpJiMY95WsgPYjX2F9PpN+kdfIaVbp08a1lc+pQnNye4twWFeWRIoxd5GCr3XJtr3Abk8gDU5qW+fFLPh0w0ZvCZZsPh72ALJFhXhe9tGlkz3/8AyWrBgpkMbMbKCSeQBJ91YnOMFmTwjeFcpvEVl/AbYboxiX1CAeZ/C9UpeJ0LbOfkXo+F34y8L5s2Yroli0F+rzD9HX8KzDxKmT9Pmaz8OtXGH8mJHUgkEEEbg6EelXVJSWUUpRcXiWzMVsahQEnh5fOBGGLHYKCTtroN9L1U1NSlHq9Dp+G6t1T6GtmP8JHjJAhRMwkvkJyjNa97XIF9CfLWuZ0o9HKcIvDZFi4uwHaGY997fACsdJv0kvDcSDm1rAAsSe4eFauJq44JC4lbKds1iPWw+0isYYwVviKjM1hsToPjV3S2OMsdmc/xPTqdPX3X7DnF8Phw8bQyyglnjkFrkF41xEUsZeMPlyuynWxKn6JOnTyeYEfEVLBnM0bWGgUsMoB7KorKLKNgo0FaT8rN689SwQ4cPKYzKFLLmyCwJJNr6ADYfzqg4xzg6KUsdRiR7HKwZWFrgjUHuty9a1cH2GexmtDJkeO32ePnWYyaeTDSawyTghELtNma3spHYZjrcM5vkA02Uk30ta9dCq7reClbT0b9iTJjUBK/kcA8GOJzep64G/lapyA9Lhop9IQY5eURbMsnhEx7QfuRr5uTE2UgWHonxjGYMZJsNiHwu5BikBjvqXRitrd6k2O+hveGcGpe0reJfR/P/BrZXGyPTPj6o6JgcXFNGJYHEkbbMvI9zDdW8DVqjVKx9MliXp/HqcfUaSdW/K9f94N1WioM+DcQKMEY9k/A/hUFted0XtJqOh9D4LJeqp2DJoBVjsdfsrtzPf8A6VDOfZFymj70hZiJ1jRnc2RFLMe5QLk+6q1sumO3PYsyfSsnBOkfG5MZO0z3AOiLyRPor58yeZJq7RSqo479/izmTk5PLFlTGg24aeqgln+m98PD3gsoM794yxsqX75/CsAkcOwjSYWJVJU/lUhzD6I6nDm48dNPEioNTeqYOb/1lnS6d32qtf6i98O4agzSFVvIS5AAAuxuSfftsK8vbdO2XVNnpoxhSuitYx37jJmAF+QqM1SyYjlvqpHofwpnAcMcor3Sfh0c47a9XMNnGx87b1b0uslRL4d0R3aBXx2e/Z91/wCFBxvDJovbQgfWsSvhrXoqdTXavcZ527TW0vE1/BEqcgLF0KLpiUYRkq/zROgy5wXDa8gqM3kDVfULqg1ktaWXRYpYOmrC4xEcaKowscIIOl+uz2AA3XKoYdxziqb6ehJF1Ox2OUjX0i4fhFgkxEwCLGLllWPMxOw7VrnQ7n31iFXWby1cqmlyVnjXQpgimDKcocnSzNoCi+J0tfTe9QuODpU6tPzFUxWDxEaqZI3VVNlJGl97X/3tWmC4pxk8Ji3ESn1Ot6uaWrL6mcnxTVOEfZLl/sRye+ujg86eXGh8qxJbG0Xho6DwKKXDYSENDdd3OazKWa+i2sxAIvqDXGsSlLJ3K8xikT+KcFhlRgY1uSWB27diATb2vWtITcWSSgpLdHPeI8DxMCAuqkC+q3NgOZOlt9O+rKcJPYqSrnFEN1t5cqjZqbMM4BBZcyhlYrtmAYXW/K4JHrUlLxNGlizBkzF4mTFzqSq9bJlTTshm2DHu0ygnuW9dNHNPcnE+rumEYouxmW6ySnm2b2o4zyQEaWzXO2QY4xIRP1yEo0qJLdSVIZ0BksRqBnz0QGnR/js/W9hrYltEc2tORtDONBJm2Vz2gxAvY3WKyqM1v+vdfIznbB0Po30ghxseaPsyKLyRE3K/pKfpJ47jnW9GolCSrt/KXr8/icvVaPCc6+O69Pl8BrXQOcWfh+NBjUsdbWPobVSnXiTO3RenWm+Q4nibdgc9/LuqtZLsdPT15fUxZUReKv8AKXiCnD5bGxdkT0LAkeoBFRre+C+bK+peInFa6Rzz1FGzMFUXZiFUDmxNgPMmwrDAx6QSKJFhjN48OvVBhs7glpZP2nLW/RVO6iBZeAYTq4UUk9o5z4FgOXkFHpXmNdqHba1nZbHsPD9LGilSx7zWS5ooAAGw0qmaN5FzO0jZUOoLW1tta2vvraEHN4RPhVrqlxsGAwBkJIynvuNP3kNWKtO2zW3URiv9/wAkmfAwxsglyoZmYRDMe1kKgrcnUtcWA1tc8r1bWii11YKT8Ral0ZFPSfhkJUhxYAZu8x65SwJ1tsSOYv4VFCUqLl7Pv2N7q46il+07cM59huGys5VUzZGs1/ZuDqCdL+mtegdsVFN9zzaqk21jg6Hh3gGHMXVsCUKaMCYwyuMqvucvWSBSRcBqoym85L6gunDG+H6QpoHRhrupzW8TsT7jUfSTdYzl6rExFQVkjYi4IuLqcy3B1BB5aUy47Ix0xnhyRJeTKLsf9a0bwsskS9Dm/T7jfZ/JlBuSGdjtbcKvrY38PGrGlrUl1Mg1eplBqMNn6lFroJJbI5bk3uwrJga9FsOHxKBtQt2t3kC4+Nj6VW1UnGp4LOkgpWpMv8JlaaV3YdV2VhTmqgdonlqdfEljpz587IyhhHUrpcZ5ZuxeGVwqs7LmJCqrOrMRa9smthcXJIGuvhpXCTWUbWWxi+lkGfhpfDNCzlrggMdWym+W/eQLedq1UsSTJOnMelnNMREsbGMNfKzLc7kg2vbkNKsS33KLSjsaiw299IxeUat4RbuhvEWM+WNI41EchVEVczEIdDKbuzEX3YC/ICuml7qOdLkaiFMRkWREl6wgKyqqSEZbhkdQDcpaYAhl7Mq20FsmCucYWOPExOpEuHARUawIdYgsclwRbNmDG23aU7EE5MEDjE8fXu+Guq3DJoBYgAmwAFhmvbQaW0oCTiMc+Gx0ssJytHPJl7rCRgVI+qRoR3VpOtTj0synhnZMNiVljjlT2JUDqO4EXt5g3HpU2jtc68S5Wz/I4msq9nZtw90SEdraVYa3IIymlsM5nuxPea473eT21cemKR4oblV+U6Itw+Qj6Dxt6Zsp+9Ucdr4P5orale6cXrpFAbcEPVLLijvEMkXjNIGCn9hA8nmE76wwLcLhJJNIo3ktpaNWf07INDKOgqNK8XLlnvoeVDPDcR5N3Wv46/bpTJWnR3RM4Rgg9idslj43NzXR09Swn8CrqrWsr4k/HJPHi4RHGGwskQBcW7EgvmDC17nTnbTaunOEVFNHFrtnKbUn6kvGYZJVCSIrhWEiZlvkcWsynkd6jU2lhErri5dTKPxvGK8k0YOrjqx6jU+iqW9R31z665Tu9p2z9F/J07rYw0/s++P3/ghE5MqJlUDXW/fe53LEnmBrrXTS6nuch+6tlk1YiMrGHEiuhazZcwIZr2zAqDY2tepJU4j1RkmiKGozPolFp8k/DKAoy2t4VATs8RcQeCXMpI1Aa3NTyPlrY8rHvrWabi8G8HhlskJJ1N65sbHJbluUccHNemqXxhHeFHwFd7w2PVBJd2cXxCfQ3J9kJEw95BHrq1uyMxt3hRuba2q7fH2cpR9Cnp5+1jF+o7xPRhusjEZPVyaFt8hAuxO2mhte2uh13pR1Kw88ovy0j6ljhirhWMEM6SA3VW32upuCbeRvaprYdcGmQ1T9nYn2/wAHUYVzDOtypsbjUajQ+oridLR3etETiGBEkuHlIObDlimpAuTcEjnY6+P2yxtcY4wRumMm236EqR8ov3VCTr0OXcU4PNJM8kURKPKUB72vYm29iwbXarkZJLDZQtg+pyS2yQcZw4w4gwym5Qrmy9xCsQCedjbzqapKeGitb7mR3w2bDRSrKs09lJunUJmKkFXTMJ7aqWGbS172q9uURl0l4uwQLh1ywyXAnvdnDC7x90O7Xj1YBiL5GscGRLhhmwswP9XJG6+GYOjgfrWjJ/uhWTBnhUIS2JlHzaG8an+ukU6IO9AbZ22AFtyBRsC53JJLG5JuSeZOpNZB2vovA0eCwqNv1eYg8s7M4HuIrTQbuyXZy/ZYOZ4k/fivRFx4bgAY1J56/E2qayfvMk09Ga0RSK5x6aO6Rihkj8SwSzwyQt7MqFCe64sD5g2PpUN2VHqXKeTSyPVFo4bhOBMRiBKwjkhJRVJHblXMzIL6t2UYC3N05XroxmpJSXc5bWBvipRDBhYoxhgTEs/Wzdsl5rFiiMpQZMqpmIJ+b0tY3yYFeIxuIksZcaWXmvWvYC17BAMo2tYDcisNbbG0Wk9y28MxKvFYshLahlvlvsRcgG2w2515TU0+yscfQ9hprnbXG1fmifw/EoqlH01ve176Wsf98zW1FsIpxkbX1TlJSj6E3A8SjQ2UG21gD38qnr1Fa2RBdprJbsaR4+ONDLIyovPOy6a2F9d9tKu1tvhfkc+7bl8dymdKvlBUgx4TUnQyFbKBzyKbEn9I/Gri07kvf/Qoy1Sg/c3+LKXwjFESliSWIaxPedz7qkuilXhEFMnKzMmWtcOBodSbAnvJ9o/YKpl0g42yp1fOQox8lDk+tyKkjNKDj6tEbg3ZGXon9SdgrBMwOltR4jnURKzdhuGHEysoJAVRcgX1voNxyvWljaWyyb1xT5Zs6bY2eFFMLMDrfKAea25HxqHw2uufV1jX2Sj09D9SZ0r4bh4IFYLmnmteRzmewUXsT7OuUWW25q//AMeduo1UpS8kP0y9kee8auUKVDvJ/RHn5PI4ZeuhkjQspEikqpbKdGsSL6EL+9W3/J42VThdF7PZjwS7MHW+26GvEYQuYn2b28dTlri1XdW3c9Wt4nN+JdFZozeMdanIr7VvFeZ8r+ld2rVwkt9mce3Rzg9t0b+A8fxeDIGSTJyBDKR3gEjUfonSsyoVrzW9/gK7JQXTOOV+xZ4+loxDAHOWAuAwsAOdraf+Kp6jT3QXVPg6GnnS30xWBRi+kZMqp1bWzWv8LgC9/wDelZehlGHVJmXrFGagolk4ZgMvzjDtHYH6IPjzbx5bDxoSl2RNJuTyyodLYBJLMUUdZCQXAGrxGOM5/Eo2YN+i6nZTbs6T+zH/AHucXVN+1ZXkmTqmQp2ywYP2drAZTcXA3OhF763sKslcxhMdJFmyPYMLMCAyMO5kYFWA8QawB3jOJGKERmDDrLIRJIOpXsqARCGjN0DnM7Wy6Bk0uTYBFisU8jZ5GLNa1z3DYDkFHIDQVkFm6D9FDiWE0wthkPMfnSPoL3r9Y+m+0Fk5Sfs6/N+3x/g1ssjXHqmdagjMkgHNj7hz9wq/CEaa1FdjiLqvty+5b0QAADYaVUzk7qWFhCbiEWVz3HX8arzWGdHTzzHHoRq1JwoDmfyscAsRjIxo1kmHc2ySeuinxC99Y0s+iXsnxyv4KOorw+pFHwfFpI06shJIrk9XKuZQTuV1DRk96Mt+d6vFU2nE4Nt8NKnf1WIFvRZIXP8AFWMME3B8VwkQ7K4s63sZIbeIv1Wx8uQ2NV7tLC3eSLdGstpWIP4lywODEkSPcgsL99eft06UmsnoatdLCyiFMyGUxIxPV/nGGgBN8qDx0JJvpoOZt2vBvCIXS67d0ux53/kX/IbtNT00bSffnYcYHARyJlN8oN2jOUo2twbEbX5A7ivQXeH1RtU0sHmtJ45dZp3W936vlEP/AJMijDyKEJeRezILqsRcB0TudlJs2pFwBY61x9ZcozlGHCX1PQ6CmUqYys5f7fyeG4FAysIo0jbKfojTxDWvVSPiEehxtX5oxrvCr9NYr67MwT3TIWMuFvbUEG3jcaVqnkvpprKI3FcN1kdxuNRWTJCgxR6vLzY6/YR8KGxZuhWKKxzyWuMygHvNiT6a1DbLpWSO+72NXWWKHiReyKoDHe/sgd9uflXEnFxeWyPQReoi7J8L9xbx7h3WOrTMXyjYdkEAk20Gn87Cun4X4tPRpwiliT39Sxd4RpdXJSknlfHY1QYaOBhNBGFa1r3Y3B1tYm1jXpNSlrK+ix5T4/k1p8O09Un0Rwxg+IDDMOevxryj00qrHGXYvcLBGigQnRsosSe6w3NjtU8ItvBiUulbnO+M9JDMMuQWDXVr7jUA2tpceNdvSUqifU2cy/WKyPTg1RuyRoQLM3bzD1AA9D/FXUxGyOGRqUoRTXcndFxfFR3F9Tr45SffVHxPbT4RLplmeWdBrzR0Tl3SHG/02SWFyCGGV1NiCqqpIPmDXe00WqopnE1ElKxtEd8dE+suHGb60L9TfxKFHQH9VVHhU+CEynEkj1ggCMNpJG611PevZVFPjkJHIimAeOHcMxGKc9THJKxJLMLkXOpLOdAfEmo7LYV+Z4/30MpN8F86P/J9HHZ8YwkbcRIewP133fyFh4mtYq6/y+7H17/kirdrK6tlu/oXUnYaAAWAAsAOQA5Cr1NEKo4iv9+JyLbp2vMmP+AYPKOsO7beX+tRXTy8I6Wio6Y9b5Y4qEvkfGYfOtuY2rWUco3rn0SyJCLaHcVXZ0001lGKGTXicOkiNHIoZHBVlOxB3FR2Q6ltyuPmayipLDOFdK+j74Kcxtco12if6yf5hoCPI7EVb09ytj8Vs0cyyHSxNU5oYNAXXiHSQRYSJIWBkZSCwN8lt/2tdO7furmVaVytcprY6Vup6a1GHJK4Fh7RsebuWv5WUfZevV6CHTVk8X4rL2lriy28POHAD5irKDmBOp9OY7rVQ1L1vW4LdS4fodDQU+GxqjPhx5T5f8/AWY4pjGF7q+GnjkXS90KhivduD+6prka2v7LJwe+Ud3Q3/a61NbYZNw8BUtbXsnb00riTfGfU6viVis00l8ivY49rcHL2mty5ge/7K6UPKUKnmK2I8bHqltuALe+1bEpEj4K7dskiMsRYb7lSMx0XUb671KorGcktNTsk09ku/r/8LfhcPliWMBVVdlW9vMk6sfGubfJSliPBHrdIro9MXwT4cDkGcncDmBbmTc7a8+QFaS0/VHczoYSpr9m/XJBmxYb2TnY6C2v/AIFU69NOc+lI7MYdCy9kEwIQIouSAPxNewjKFNa6nwjnzl1SygkIRLX8PEmuDOcrrHNhCnifGYoEHW37fZCruRz0uNBz9K2rg7JYiYtsjCOZFejxfC9upfu+kf8AHV/o1P4jnqel/CMMUiMMmUBBsO7u8q6Wm0fsn1yeZE9k1KPTjY9cLjCzwhRYAt901H4p/Y/NCpYksGOlvSDSSCE6he2w5dpQUHjYm59O+uXpNNn35fkRarU/cj+ZRK6ZzS09HOg8+JVZZCIYW1DMLu470Tu/SJA7r1A7nKXRUup/T82a2ThWszeC8cN6G4GH+p65vrTnN/7YsnvBqVaW2f8Acnj4R2+vJRs8RS8kf1H+fQKNFGygAAeQGlWKtLVVvFb+vLKNupts8zPNWCAncKwPWNr7I38fCorZ9K+Ja0tHtZb8ItIFUzuJGaAKAhY/B5tR7Q+NRzhncnpu6Hh8CkioToJp8GKAW9IOCRYuEwyjxRhujcmH8xzFRSUoy64c/uRW1qaOH8d4LNhJTFMtjurD2XX6ynmPiOdXqro2rMf/AIc6UXF4YvqU1HHBOENimjjU2F3Lt9VfmwT4nUADxqvqLlVHqf5EtVbseEWLj+BnwkEckbWs7iS2oIZgYybjla230hWmj8Rk7Gov5IreJ6FKtTa45+XYh4fikrgfOqFJ1YJqO/mdvKuvLW2qDkmedrrUro14w28Fmw3FMMihRLfvJDEk9503ry13trpuc+T3+nrqorVcOES4MTFMDkYkC17Fl77a6VC4yhyTpqQPw2I7qT5s/wCNPaTMOMWeRwuEWsm23abz76z7WfqOiIYjDgKoBYDMBbOxFmYBtCba3qamycpYbNk8NYJPBMEwUvIbINbHaw3PgK3nBSkSaicc4Rrm6TwE9mUAcuy3+Wo5KxvZFdOJGPHMP/aDXwb8Kj9lM29pH1NmF4rDI4RHuzbCzDkTzHcKOqZjrRoF5GzH0HcKPb3I/mT1w6mc96dAjE2BLNYG52AOoUDYc67GhpThnBxvE7XXZ0JiKN5Ab3GldFVI5ftpIfwdI2HtoG8VNj7jp8an6mWYa5pYkhnwbGtiZssIZGjRpCzWta4BAIvqb1V1l1UYf1FnLwW6dQrW1HbY2P0ZUQJN1jfPuisMosgaQFmvfW1r61y/tT9pKGODX2HuxlnkV8L4bFJj4oAxeIzKtyLZluM2nK+oqadslQ5vZ4InFKeEdnka5v8A78B5V0aKo11qKPNXWSnNyZ5qUiCgJOAwTStYbcz3f61HOaiT0USteFwWrDQKihVGg/3eqbeXlnchBQj0o21g3CgCgCgImMwQfUaN9vnWkoZJqrXD5CiSMqbEWNQNYL8ZqSyiPPi0T2mA8OfurWUlHklhXKfCEPH3hxUZikizLuCdGU/WUjY/bzqs54n1x2f7k3/XdfnZW4ejmEiFzGDbUs939cu3uFby1Fsu5KtDp6o56c/Mk4XG4JJOsSS1kyZVRgtswYnRd9BVaz204dMl3yVMRc3NEyTjmEdSrPmVhYgo5BHMezUKpsi8rky+maw90VLGcMwiMXhxDKm7RsjtfwVjbXz99dOrVW4xOOTjW+EQc1KEmv8AHyG2PiwOHVOvGXNoLmRiSAL+z5jkKrZtk30nalWqklMb8OwsSIHiFlkAYG51FtNDqN6gs6s+8bqKXBKqM2Chg0YzZf10++Km0/8AcRh8oMRbJ1LCQoxtlAkbx1IuVXzsK2bsyzMq0ue5E/4Lhv7P4v8AjWOu02+zP0D/AILhv7P4v+NOu0fZX6EHE4nBYaVV9ibTLYSH2iVGuoHOs9N0lsaOMYSxIcxJasQjg6UIdKOOYxpGkNyWdnym+5Ym326V6iLjCCxxg8JPqnY87vP+RoeiXEP/ALVvR4v89Vv+x0/4v3JnoLl2Mp0S4gdPyZvV4h/irD8R0/4v3H2G70Lv0N6MvhY5WlsZZRaym4VQDZb8ySbnlt3Vx9brY3zio8I6el0jqg88sWcYxsq4KJB2UuEY31Y9omxGmQW35+Q1yoxdsplhQlGmLY3wHR7DwzxzxqwaNswXMcp0I1vcjfkazO+UoOD4Zbl4ZVLdbMsseNU73H2V1KtfW9pbHl9T/wAe1Ne8MSXw2f6ElTfbWr0ZKSymcOdU65dM00xpgODs+r9lfifwqKdyWyLVGilPeeyLDBCqAKosBVZtvdnWhBQWImysGwUAUAUAUBpxOIVFLOQFG5NYk1FZZtCEpy6YrLKbxjpA0vZQZU7/AKR9fo+lULdQ5bLg7+k8OjX70939BLVY6aWAoZChrLhlZ6Ir/RZR+kw/gWpZ+ZFDSr+lL8yd0R/6VPNvvGtbPMTaP+0iN01HzUf94PutW1fJpreI/M99Lxonm38qV9zXW8RLRglUwxuovZFDL+yNfOtJxT3I4p4UZfkxRgMc3akcF4w8oNgOyqlMt7a7E9587VN7CtzUcc4K8LMRbl2bJ7cdwVj2iDbQWferX/WNcxI3qYY2kJMH0hTqkzqzyC+aygC4Y2NzYbW2qarw3L6orBpDWQUPe3Z56PY3EdaqiViGbUMSw77C+1h3Wqzrq6IV+8ve+BX087JT2exYMWO23ma8++T01PkRqrBKVrj4/pMfiE++1Sw8pzNUv6y/IshYbnbeo0nk6Dkkmzk3BJRLioXYaPKGt4lrj42r0N66aHjsjxWmxLVxz3l/JdOBQdZJiFcuRG+Ve2wsMzjkddhvXCnhJYPS0VRnKSfY9dGsOJY3aQuSJCo7bjQKp5HxNYns9jOlpjOLcvU99I8GseHZ0LAgru7nQsAdCbUg8s21NMIQbiaukq/0OHwKf/zasw87Malf0Y/kWaojoLgKGTZh52RsyMVI5j/etbxnKPlZDbRXasTWS28E6RCQhJbK50B5N4eB/wB+FXatQpbS5OFq/D5Ve9DdfVFhqyc0KAKAKAKAKAqHTTEHOkf0QM3mSSB7rH31S1cnlI7fhFaxKffgrlUztBQBQAKGGIeiafMyD/1GHwUVJPlFLSLMJL4sYcFwJhhWMkErfUbasT/OtZPLyWKK3XDpZA6Xj5pP71fsatq+SDW+VfMz0tHYQ/pH7DSvk11vlQ74YzBUy75R9g3qKU1HLZPJR9muo19HlBSYECxnlBHLfatdVNqyMl6I5NCTg0/VkPFdGtyj2G9mH8x+FdanxzMemyO/GV/BWs0XeLF/CeEKYVldiQxOVFHaYl2AUE8zW0vFZQ/pVx3Xc0r0qaUpPYYdEc35ZiEYKvVKFCrqB2tdTv586qWOcnmTyy1XiKaXA1na7MfE/bVZncrWIJGusEhXePj+kQ/s/fNTQ4ZzdWv6sS08R63ExiNRZkIYOq3K6EHTbUEip43dSx0kS08dNZ1OWU+zOZ8R4YYMVFIpzIGRyQAtsr9tct7ggDbx8KtxuXsXGXO5Ws0VturVtaWFjuWbo3+exVtusBHqXNcyzhHS03ns+Zv6MQMkcgZSvzrkXBFxZRfy0rWbyyTSRcYvPqeulY/osn7P31pDzDVr+kzRxvDs+FjVFLEGM2AubWtWYvEmaXQcqopfAe1GXFwFDIUAUMM6FwLEGSCNjqbWJ7yCVv8ACurU24Js8lqoKF0orgYVIQBQBQBQBQHKflI42MPxKMP+bfDpf9EiWazW7u//AEqG6n2i25L2h1fsJYlwz1FIGAZSCCLgjUEeBrmtNPDPSxkpLKPVYNgoAoCLw/ArCrKpJDMXN7bn02rZyyRVVKtYRKrUlIvEMCsyhWJADBtLbjzG1bReCK2pWLDF3SwfNL+v/hatq+StrV7i+Z56QTvHhleN2UjKOySLgjnbesRipS3Rrql/STNXFnliSFlmmu7Kpu52IubUUYtvKI7alCMWnyNvyFv7fEf9z/StML0RZ+yx9WVrifGXwuJJJeRUAy5yWtmAu32jS29W9NKMJKbRz9Rp+tzpi8ZRqwXSTqsVJJkHz5Gl9ueh8eXpXSrthHUS9Hwct6Cc6FDO8PrgukbhgGBuCLjyOtcScXGTi+T1dclKCa4weq1JBBx4fPweY++Klh5Wc/Vf3YFlw+LdPYa1+WlvjSu6VawiTUaKu95lnIvm4bC0jSNGpdjmYnYnmbbfCsu+TJIUOMVHqeER+F4Fo5J2NssjgrbuseXLetJSykYpqcJSb7jKtCyQeN4VpYHjS2ZgLX0HtA/yraLw8kN8HODiiXAllUdwA9wrD5JILCSPdYNgoAoBdxri8eHTM5ux9lObH+Q7zUtdTseEVdTqoURy+eyL38meIaThsDt7TGQn1nk+FdNRUdkeWnNzk5PuWismoUAUAUAUBz35W+iEmLjTEQDNLCCCg3eM62Heym5A55jztWUwcb4VxmbDn5ttL6o2q356cj5WrWymNi3LFGqspfuvb0Lfw7plC9hKDE3ee0vvGo9RVGekmvLudinxSuW09n9CwwTq4zIysO9SCPeKruLXJ0oWRksxeTZWpuFAFAFAQOM4EzRhVIBDA637iP51tGWGQaip2RwiF0sS2EI7sv2gVtX5iHVrFOPkY6QRkxQWBNpY9u6xFIcsxqF7kPmh7UZdRWsTgklxssbi6vBr70sR4ggGpE2oZKXTnUv5C7C9FEeSaFme0eXI+gOov5G21buzETFdX9aTLVwrBGJMpkZ/E6e4cq1tudmMosVUqvOHyTKiJxdxLh7SSROCAENze+uoOnurZSwsFa6lznGS7DGtSyFAFAFAFAFAFDBCx/FoIfzkiqe692/dGtSQqnLhEFuqqq80ir8U6ak3GHS36b7+i7e/3Vbr0n4zlX+Kt7Vr82JOE8MxOPxAjjvJI+rM2yrzZj9FR/oKuJKKwkcic5TfVJ5Z9J8C4YuGw8WHTVYkC3O5I3Y+JNz61qYJ9AFAFAFAFAFAU3pf8nWFxpMg+ZnOpkQCzH9NNm89DpvWUwcl6QfJ7j8LcmIzRj6cN308UtmX3WHfW2UCrwTMhujMrDmpIPlcVhpPkzGUovMXgdYTpXik3cOP0wPtFj8ahlpq3wsFyvxG+PfPzG+H6cj+shPmjX+BA+2oJaP8LLsPF/xR/QYwdMcK3tF0/WUn7t6ilpLEWYeKUS5yifDx3CttPH6sF+9ao3TYuxYjrKJcSROjmVvZYHyIP2Vo4tdidWRfDIHSLCPJh3RBdjaw0GzA8/CsweHuQ6mDnW1EYRiwA7hate5PFbI9VgyKlwr/AJaZcvYMOXNce1mBtbfat8rpwVuh+36sbYGtaFkKGQoYCgyFAFBlGibGxJ7ciL+syj7TWyhJ8IjldXHmS/Ugz9JMIu8yn9W7fdBqRaex9iCWv08fvC7EdNcOPZWR/QAfE3+FSrRzfJWn4tUvKmxXium8p/NxIvixLH4WqaOjj3ZUn4tY/KkhPjOPYmT2pmA7l7I/htf1qeFEI8IpWay6zmX+CJgMFLM+SGN5H+qiljrzNth4nSpNisdB6O/JFiZLNi3ECc0WzyeV/YX+LyrGTJ1vgHAMPg4+qw8YQbk7sx72Y6sfs5VqBnQBQBQBQBQBQBQBQBQCjjHRjB4r/qMPG5+taz+jizD30BTOJ/I5hGuYJpYjyDWkUe+zfxVnIKtxD5IMcn5qSCUebRt+6QR/FWeoFdxvQbiUV8+DlIH1Msn3CxrOTAkxWDkj/OxyR/roy/eApkEcEcrUBIjxci+zI48mYfYaw4xfY3Vs1w3+pJj43iRtPJ6sT9taOmt9kSrV3L7zNy9JMWP69vch+1a1+z1+hutdqF949jpRjP7b+CP/AC0+zV+ht/2Go/EZ/wCasX/a/wACf5afZq/Qz/2Oo/EZ/wCasX/a/wACfhT7NX6D/sNR+I8HpPi/7Y/ux/5afZ6/Q1/7DUfiNTdIMUf69/Sw+wVn2FfoavW3v77NL8VxB3nl/fb8a2VUF2NHqbnzJ/qRpJmb2mZvMk/bWySXBE5yfLNQIvbS9bZNRjhOCYqW3V4ad781icj32tTIH2B+Tbikn/0/VjvkdFHuBLfCsZBZOG/IzMbHEYqNO9YlZ/czZbfumsZMls4V8lXDorF1ecjnK2n7qZQfUGsZBcsHg44lCRRpGo2VFCj3CsA30AUAUAUAUAUAUAUAUAUAUAUAUAUAUBhhQC/FcBwkv5zDQP8ArRoftFALJ+gXDH3wcQ/VBT7pFZywV3i3yfcNS+XDkf8A7Z/89Mgo3Gej2Gj9iO37bnmO9qymYKdikAOlbA00AUAz4XhEcjML7cyOY7jWAXjhHRLBvbNETf8A9SUfY1YyZLrw35OeF5bnDXPjJMfgXrGQOIOhfDk2wWH9Y1b4sDWMsDXC4CGP83FGn6qqv2CgJNAFAFAFAFAFAFAFAFAFAFAf/9k=[/img]
Central Angles Forming A Rectangle
Let's Solve
[img]https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTn1YON6eloOxeYQzikjnIk6p4i8xXnQRnUcQ&s[/img]
Formula in finding the area of the sector given the arc length and radius.
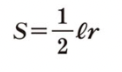
PRACTICE 3
[size=150][b]Find the sector area.[br][/b][br]Given:[br]r= 6 cm[br]l= 4 π cm[/size]
PRACTICE 4
[size=150][b]Find the sector area.[br][/b][br]Given:[br]r= 9 cm[br]l= 14 π cm[/size]
Let's Solve
[img]https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTn1YON6eloOxeYQzikjnIk6p4i8xXnQRnUcQ&s[/img]

PRACTICE 5
[size=150][b]Find the central angle of a sector with a radius of 12 cm and an arc length of 10π cm.[/b][/size]