Stetige Zufallsgrößen - Normalverteilung
"Die Wahrscheinlichkeiten ganzzahliger Zufallsgrößen kann man mit Pfad- und Summenregel berechnen. Bei reellwertigen Zufallsgrößen geht das nicht mehr. Man greift auf Integrale zurück und erweitert damit den Einsatzbereich der Integralrechnung erheblich. Im Mittelpunkt steht die Gauß´sche Glockenfunktion, die als Normalverteilung eine Brücke schlägt zwischen Analysis und Wahrscheinlichkeitsrechnung. Der zentrale Grenzwertsatz erklärt, warum die Normalverteilung in Wirklichkeit so oft vorkommt."
Table of Contents
- Stetige Zufallsgrößen
- Normalverteilung
- It´s Teatime
- Integrale besuchen die Stochastik
- Frage: Wie lautet die Funktionsgleichung?
- Frage: Wie lautet die Funktionsgleichung?
- Die Analysis der Gauß´schen Glockenkurve
- Wiederholung
- Der Einfluss von Parametern
- Zusammenfassung
- Annäherung an die Binomialverteilung
- Annäherung an eine Binomialverteilung
- Die Gauß´sche Glockenfunktion
- Funktionsgleichung der Glockenkurve
- Der Graph der Gauß´schen Glockenfunktion
- Antwort: Funktionsgleichung
- Normalverteilung bei der Servierzeit
- Übungsaufgaben
- It´s Teatime Übungen
- Graph und Funktion zuordnen
- Hochpunkt und Wendestelle
- Graphen skizzieren
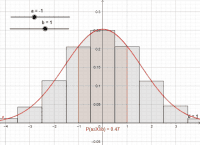
Normalverteilung
Bei einer Binomialverteilung können die Zufallsgrößen nur bestimmte Werte (X = 0; 1; 2;…) annehmen, solche Zufallsgrößen nennt man [b]diskret[/b]. [br]Zufallsgrößen, die alle Werte aus einem bestimmten Intervall annehmen können, nennt man [b]stetig[/b].[br][br]Die [b]Normalverteilung[/b] (auch Gauß-Verteilung) ist eine Wahrscheinlichkeitsverteilung, mit der sich [br][u]zufällige Abweichungen von Normgrößen [/u](z.B. die Servierzeit, Gewicht von Hühnereiern) oder[br][u]Durchschnittswerten[/u] (Körpergrößen) beschreiben lassen. Auch die Wahrscheinlichkeiten von [br][u]Messfehlern[/u], die auf Zufällen beruhen, ergeben häufig eine Normalverteilung. [br]Außerdem können Wahrscheinlichkeiten einer [u]binomialverteilten Zufallsgröße[/u] mit der Normalverteilung angenähert werden. Dies ergibt sich nicht nur aus den Überlegungen aus Nr. 2, sondern besagt auch der [b]Satz von de Moivre-Laplace[/b] (s. unten). Die [u]Sigmaregeln[/u] können so begründet werden.[br][br]Die Normalverteilung kann mithilfe einer [b]Glockenkurve[/b] (Gauß’sche Glockenkurve) beschrieben werden.[br][br]Die [b]Wahrscheinlichkeit[/b], dass die Werte einer Zufallsgröße in einem bestimmten Intervall liegen, kann mithilfe der [b]Fläche unter der Glockenkurve[/b] auf diesem Intervall bestimmt werden.[br]Für einen singulären (Einzel-) Wert degeneriert diese Fläche zu einer Fläche mit dem Inhalt Null, somit ist[br]die Wahrscheinlichkeit, dass die Zufallsgröße einen singulären (Einzel-) Wert annimmt stets Null.
Fläche unter der Glockenkurve
Satz von de Moivre-Laplace
Für binomialverteilte Zufallsgrößen X mit [math]\mu=n\cdot p[/math] und [math]\sigma=\sqrt{n\cdot p\cdot\left(1-p\right)}[/math] gilt:[br][br]a) [math]P\left(X=k\right)=B_{n;p}\left(k\right)\approx\varphi_{\mu;\sigma}\left(k\right)[/math] und[br][br]b) [math]P\left(a\le X\le b\right)\approx\int^{b+0,5}_{a-0,5}\varphi_{\mu;\varphi}\left(x\right)dx[/math].
Eine Funktionsgleichung der Glockenkurve wird mit [math]\text{ }\varphi_{ }[/math]. Was genau [math]\varphi_{\mu;\sigma}[/math] ist, werden wir noch rausfinden.
Übung
Frage: Wie lautet die Funktionsgleichung?
Karl Friedrich Gauß (1777-1855), [br]war ein deutscher Mathematiker, Statistiker, [br]Astronom, Geodät, Elektrotechniker und [br]Physiker.
Wir haben schon gelernt, dass es eine Funktion gibt, die nicht nur die [br]Binomialverteilungen beschreiben kann, sondern sich auch eignet um Messfehler [br]darzustellen und die Sigmaregeln zu begründen. Der Entdecker war Carl [br]Friedrich Gauß. Nach ihm sind die Funktionen benannt. In den folgenden Kapiteln wollen wir versuchen herauszufinden, wie die Funktionsgleichung der Kurve lauten könnte, indem wir uns dieser annähern. Dazu wiederholen wir zunächst einiges aus der Analysis und betrachten dann einige Binomialverteilungen.
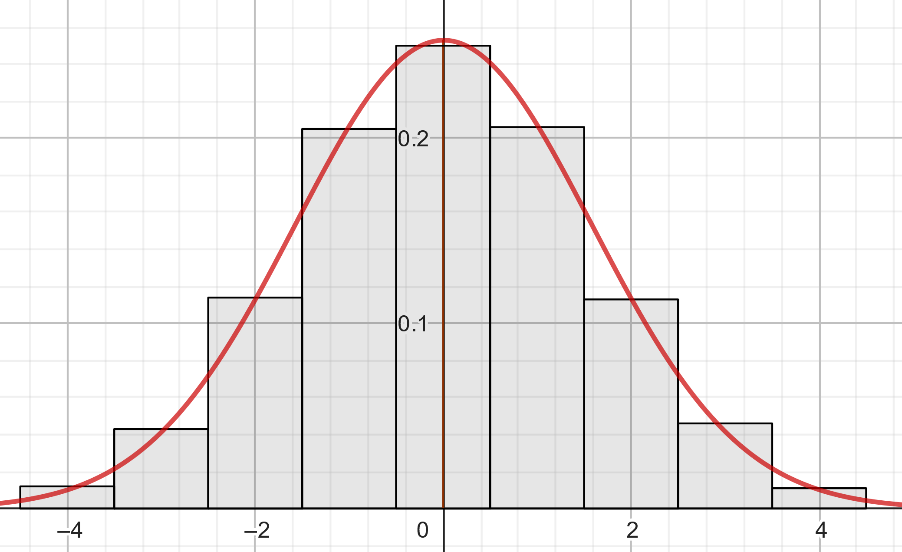
Wiederholung
Ordnen Sie die Funktionsterme den nebenstehenden Graphen zu:
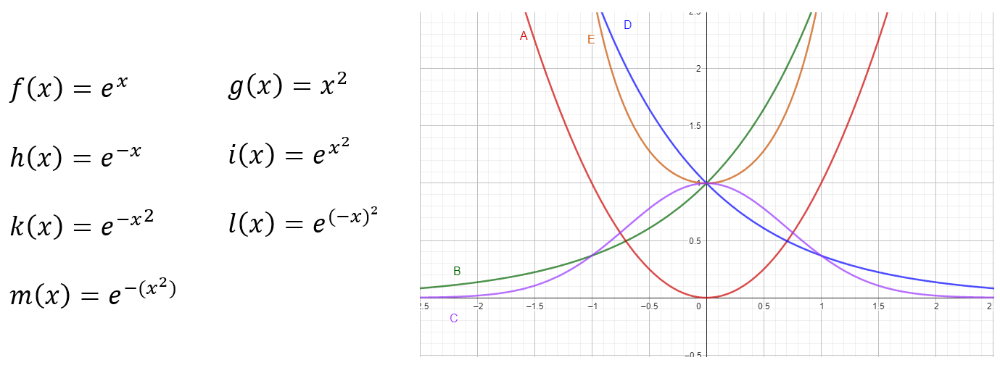
f(x) gehört zu:
g(x) gehört zu:
h(x) gehört zu:
i(x) gehört zu:
k(x) gehört zu:
l(x) gehört zu:
m(x) gehört zu:
Welche Funktion eignet sich für den Graphen?
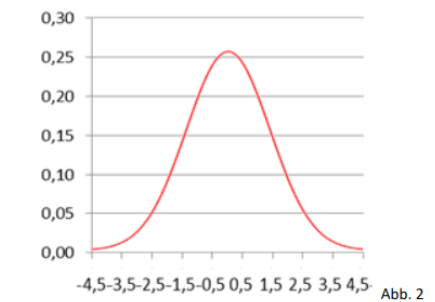
Annäherung an eine Binomialverteilung
Wir haben bereits herausgefunden, welchen Einfluss die Parameter auf den Graphen der e-Funktion haben. Jetzt wollen wir dieses Wissen nutzen, um den Graphen an ein Histogramm der Binomialverteilung anzunähern.
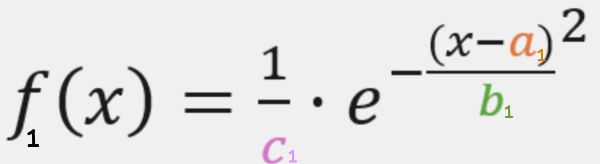
1. Annäherung
[size=150]Im Applet 1 sehen Sie das Histogramm einer Binomial-Verteilung für einen Stichprobenumfang von n=50 und einer Trefferwahrscheinlichkeit von p=0,4. [/size]
Aufgabe:
[list=1][size=150][*]Verschieben Sie die Schieberegler im Applet 2 und bestimmen Sie die Parameter a,b und c so, dass der Graph der e-Funktion möglichst die Mittelpunkte der oberen Kante der Säulen verbindet.[/*][*]Machen Sie einen Screenshot von Ihrer angenäherten Kurve und fügen Sie diesen in Ihre Notizen ein.[/*][/size][/list]
Applet 1: Histogramm einer binomialverteilten Zufallsgröße mit n=50, p=0,4
2. Annäherung
[size=100]Wir verändern noch ein Mal unsere Funktion:[br][br][/size]
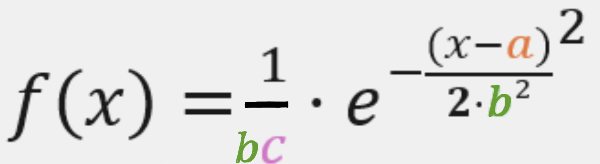
[size=200][size=100][size=150]Unten im Applet 2 sehen Sie das Histogramm einer Binomialverteilung mit n = 30 und p = 0,3. Berechnen Sie den Erwartungswert und die Standardabweichung. Geben Sie Ihre Ergebnisse ein.[/size][/size][/size]
Erwartungswert:
Standardabweichung:
Aufgabe
[size=150]Verschieben Sie die Schieberegler im Applet 2 und estimmen Sie die Parameter a und b so, dass der Graph der e-Funktion möglichst die Mittelpunkte der oberen Kante der Säulen verbindet. [br]Machen Sie ein Screenshot für Ihre Notizen.[/size]
Αpplet 2: Histogramm einer binomialverteilten Zufallsgröße mit n=30, p=0,3
Der Zusammenhang zwischen den Kenngrößen und der Funktionsgleichung
Beschreiben Sie den Zusammenhang zwischen unserer Funktiongleichung und den berechneten Kenngrößen des Erwartungswertes und der Standardabweichung.
Wie kommt es zu den Parameter c?
Die Funktion, die wir suchen, soll eine Wahrscheinlichkeitsdichte werden. [br]Das heißt es müssen folgende Bedingungen gelten:[br]1) [math]f\left(x\right)\ge0[/math] für alle x aus unserem Intervall und[br]2) [math]\int_a^bf\left(x\right)dx=1[/math].
Begründen Sie, dass die erste Bedingung für eine Wahrscheinlichkeitsdichte bereits erfüllt ist.
In dem Applet 3 wird näherungsweise die Fläche unter dem Graphen berechnet. Das Ergebniss wird bei d angegeben. Warum handelt es sich hier noch nicht um eine Wahrscheinlichkeitsdichte?[br]
Applet 3: Fläche unter dem Graphen
Verschieben Sie den Schieberegler c so, dass die zweite Bedingung für eine Wahrscheinlichkeitsdichte erfüllt ist. [br]Geben Sie an welchen Wert c näherungsweise annehmen muss.
Verschieben Sie nun die Schieberegler für a und b im Applet 3. Was muss nun für c gelten, damit f weiterhin eine Wahrscheinlichkeitsdichte bleibt? Wählen Sie die richtige(n) Antwort(en) aus.
Funktionsgleichung der Glockenkurve
[size=200][size=150]Die Gauß'sche Glockenfunktion lautet: [/size][/size]
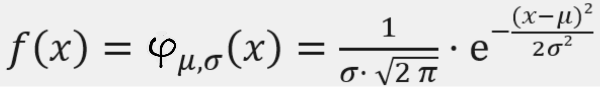
[size=150]mit[br][math]\mu[/math][/size][size=200][size=150][size=100]= Erwartungswert/ wahrer Wert[/size][br][math]\sigma[/math][/size][/size]= Standardabweichung[br][br]Für [math]\mu=0[/math] und [math]\sigma=1[/math] vereinfacht sich die Funktionsgleichung zu [math]\varphi_{0;1}\left(x\right)=\frac{1}{\sqrt{2\pi}}\cdot e^{-\frac{x^2}{2}}[/math]. [br]Man spricht dann von der [b]Standard-Glockenfunktion [math]\varphi=\varphi_{0;1}[/math][/b].
Normalverteilung bei der Servierzeit
Nun können wir die Frage mit Hilfe des Erwartungswertes und der Standardabweichung beantworten![br]Verschieben Sie die Schieberegler entsprechend und machen Sie ein Screenshot für Ihre Notizen bei OneNote.
It´s Teatime Übungen
