The Geometry of Music
Overview
Music Basics - Defining Terms[br][br]Origin of Music Theory - Pythagoras[br][br]Relation to Group Theory[br][br]Neo-Riemannian Tonnetz

Getting some syntax out of the way
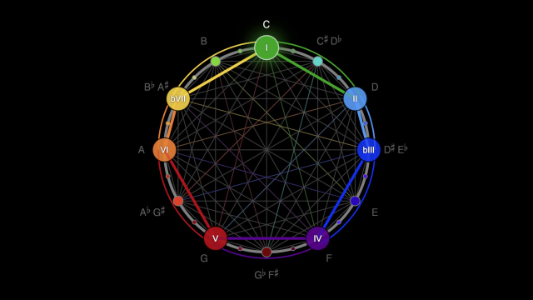
There are twelve distinct notes in an octave:[br][br][b]C, C#, D, D#, E, F, F#, G, G#, A, A#, B[/b] (going up)[br][b]B, Bb, A, Ab, G, Gb, F, E, Eb, D, Db, C [/b](going down)[br][br]For the purposes of this presentation, we'll be using sharps.[br][br]Stepping through by one - half step (semitone)[br]Stepping through by two - whole step (tone)[br][br]Chord: Multiple notes played together[br][br]Transposition: Playing a melody at a pitch higher or lower than the original pitch[br][br]Inversion: Sending a note to its complement about a fixed center/reflection point (more later)[br][br][br][br]Try it out here: [url=https://musiclab.chromeexperiments.com/Strings/]String Demo[/url]

Origins of Music Theory
As with many concepts in mathematics, music theory finds much of its origin with Pythagoras.[br]"All is number" - Pythagoras[br][br]Pythagoras observed that different length strings produced different notes, and the notes produced correlated to their given string lengths, in particular:[br][br]F = C/L, where F is frequency, C is some starting constant, and L is string length. [br][br]So, for example, if we start with L = 1, we get F = C. If we cut the string length in half, we get F = 2C, correlating to a full octave jump in pitch.
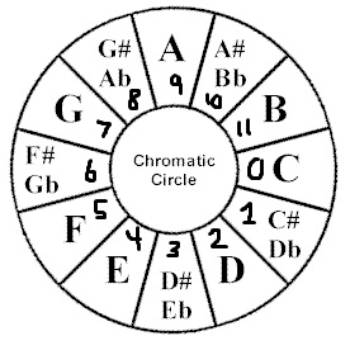
Chromatic circle
Now that we know a little more about pitch, let's talk about the chromatic circle above and its properties.[br][br]If you're clever, you'll notice that since notes begin to repeat after the 12 notes above, we have a bijection between the set of pitch classes and [math]Z_{12}[/math]. Therefore, we can define a set of operations on the notes of a scale and do all our operations mod 12.[br][br]For example, we can define transposition and inversion as follows:[br][br][math]T_n[/math] (transposition by n semitones) -> [math]T_n\left(X\right)=X+n[/math][br][math]I_n[/math] (inversion across n) -> [math]I_n\left(X\right)=2n-X[/math]
Element of the Chromatic Circle form a group under (+)
[u]Proof:[/u][br][br]We'll call our set of pitch classes [math]C[/math], defined as such:[br][math]C[/math]: [C C# D D# E F F# G G# A A# B] -> [0 1 2 3 4 5 6 7 8 9 10 11][br][br][u]Closure: [br][/u]Let a, b [math]\in[/math][math]C[/math]. Then a, b correspond to elements of [math]Z_{12}[/math], which is closed under addition, and thus a+b [math]\in[/math][math]C[/math].[br][br][u]Identity:[br][/u]C acts as our identity in [math]C[/math]. Let a [math]\in[/math][math]C[/math]. Then a+C = a+0 = a. [br][br][u]Inverses:[br][/u]As discussed, inversed exist for any axis/centerpoint. Let our centerpoint be n. Let a [math]\in C[/math]. [br]Then [math]a^{-1}[/math]= 2n - a. Since, again, every element corresponds to [math]Z_{12}[/math], and a, n[math]\in C[/math], we know (2n-a)[math]\in C[/math]. So every element has an inverse in [math]C[/math].[br][br][u]Associativity:[br][/u]The addition operator is associative, giving us associativity.[br][br][br]In addition, [math]C[/math] comutes, making it an abelian group and therefore a [i]cyclic group.[br][/i]In particular, [math]C[/math] can be generated through repeated addition on the notes: C#(1), F(5), G(7), B(11)[br][br]F0 = F[br]F1 = A#[br]F2 = D#[br]F3 = G#[br]F4 = C#[br]F5 = F#[br]F6 = B[br]F7 = E[br]F8 = A[br]F9 = D[br]F10 = G[br]F11 = C[br]F12 = F (starts over)[br][br]This also means any subgroup of [math]C[/math] will have order dividing 12. In fact, the subgroups directly correspond to the subgroups of [math]Z_{12}[/math]:[br]{C}, {C, F#}, {C, E, G#}, {C, D#, F#, A}, {C, D, E, F#, G#, A#}
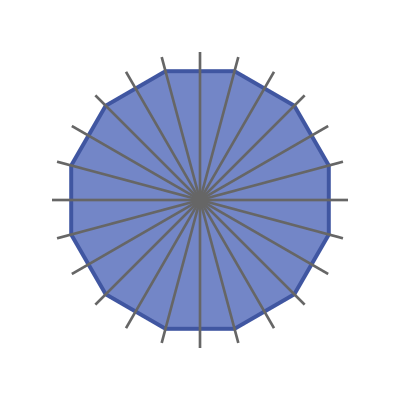
Even more interesting, the group of transpositions and inversions on [math]C[/math] is isomorphic to the dihedral group [math]D_{12}[/math], the symmetries of a regular 12-gon. [br][br]Transposition - rotation by 30[math]^\circ[/math][br]Inversion - reflection about a line of symmetry
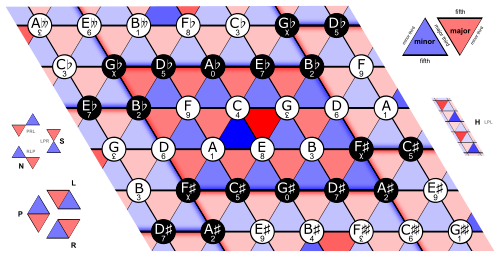
Neo-Riemannian Tonnetz
A way of visualizing chords using lattices. Every node is a pitch class, and every edge is either: perfect 5th, minor 3rd, or major 3rd. [br][br]Chords are then represented by equilateral triangles, with each reflection along an edge representing: a switch between major and minor.[br][br]Work with the following applet and tell me what patterns you can find among the lattice:
By Ewan Kummel[br][url=https://www.geogebra.org/m/HfVhzSDN#material/dheskhwy]Tonnetz[/url][br]

If we wrap around, considering the fact that pitch classes repeat after 12 elements, we can connect the tonnetz/lattice 3-dimensionally to get a torus.
Final Notes
This is just scratching the surface of what's out there in terms of music theory and mathematics. There's an entire field dedicated to it. Topics I haven't touched on include:[br][br]Higher-prime tuning lattices, polyrhythms forming regular polygons, hyperbolic music maps, chord-stratified manifolds, quasicrystal scales, and about 100 others. Most of it is way over my head but if you're interested, this seems to be the leading publication in the field:
