bilangan bulat
buku ini berisi tentang materi bilangan bulat kelas 7
Table of Contents
- bab 1
- Pengertian Bilangan Bulat
- bab 2
- OPERASI BILANGAN BULAT
- Operasi Hitung Bilangan Bulat Presentasi Hijau Kuning Gaya Sederhana
- bab 3
- PERKALIAN BILANGAN BULAT
- bab 4
- PEMBAGIAN BILANGAN BULAT
Pengertian Bilangan Bulat
Tujuan Pembelajaran
[list][*]Siswa dapat mengenali dan menyebutkan bilangan bulat.[br][br][/*][*]Siswa dapat membedakan bilangan bulat positif, nol, dan negatif.[br][br][/*][*]Siswa dapat mengidentifikasi bilangan bulat dalam kehidupan sehari-hari.[br][/*][/list]
Pengantar Konsep
Bilangan bulat adalah himpunan bilangan yang terdiri dari [b]bilangan bulat positif[/b], [b]nol[/b], dan [b]bilangan bulat negatif[/b]. Secara matematis, bilangan bulat dilambangkan dengan huruf [math]\mathbb{Z}[/math] (dibaca: “zet”), yang berasal dari kata [b]Zahlen[/b] dalam bahasa Jerman yang berarti "bilangan".[br][br]Secara umum, bilangan bulat dapat ditulis sebagai:[br][math]\mathbb{Z}[/math] = {..., -3, -2, -1, 0, 1, 2, 3, ...}[br][br]Bilangan bulat terbagi menjadi tiga bagian utama:[br][list=1][*][b]Bilangan bulat negatif[/b]: Bilangan-bilangan yang nilainya kurang dari nol, contohnya: -1, -2, -3, -10, dan seterusnya.[br][/*][*][b]Nol (0)[/b]: Anggota bilangan bulat yang bersifat netral, bukan positif dan bukan negatif.[/*][*][b]Bilangan bulat positif[/b]: Bilangan-bilangan yang nilainya lebih besar dari nol, contohnya: 1, 2, 3, 10, dan seterusnya.[/*][/list]
Contoh Bilangan Bulat dalam Kehidupan Sehari-hari
[b]1. Suhu Udara:[/b][br][list][*]Ketika suhu menunjukkan [b]-5[math]^\circ[/math]C[/b], artinya suhu berada 5 derajat dibawah 0.[/*][*]Jika suhu meningkat menjadi [b]10[math]^\circ[/math]C[/b], maka suhu tersebut bilangan bulat positif.[/*][/list][br][b]2. Ketinggian Suatu Tempat:[br][/b][list][*]Gunung memiliki ketinggian [b]+20.000 [/b]meter diatas permukaan laut.[/*][*]Palung Laut bisa berada di kedalaman[b] -4.000 [/b]meter di bawah permukaan laut.[/*][/list][b][br]3. Perdagangan (Laba dan Rugi):[br][/b][list][*]Seseorang memperoleh keuntungan[b] Rp500.000 [/b]→ bilangan bulat positif.[/*][*]Jika mengalami kerugian Rp300.000, dapat dipresentasikan sebagai -300.000[/*][/list][br][b]4. Skor Dalam Permainan:[br][/b][list][*]Seorang pemain mencetak skor [b]+3 [/b]poin karena benar.[/*][*]Ia dikurangi [b]-2 [/b]poin karena menjawab salah.[/*][/list]
Ilustrasi Garis Bilangan
Garis bilangan di bawah memperlihatkan susunan bilangan dari kiri ke kanan. Semakin ke kanan, nilai bilangan bertambah besar. Sebaliknya, semakin ke kiri, nilai bilangan semakin kecil.
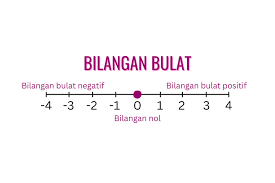
Ilustrasi Garis Bilangan Pada Geogebra
CATATAN PENTING
[list][*]Bilangan bulat [b]tidak[/b] mencakup pecahan atau desimal, seperti ½, 0.75, atau -3.2.[br][br][/*][*]Bilangan bulat [b]mempunyai sifat tertutup[/b] terhadap operasi penjumlahan, pengurangan, dan perkalian. Namun tidak tertutup terhadap pembagian (karena hasil pembagian dua bilangan bulat belum tentu bilangan bulat).[/*][/list]
LATIHAN SINGKAT
Petunjuk : Pilih jawaban yang benar.[br][br]1. Manakah dari bilangan berikut yang termasuk bilangan bulat?
2. Suhu di puncak lawu 3[math]^\circ[/math]C dibawah 0. Jika suhu tersebut ditulis dalam bilangan bulat adalah ....
3. Urutkan bilangan berikut dari yang terkecil ke terbesar![br]-3, 0, 2, -1
OPERASI BILANGAN BULAT
[b]Operasi hitung bilangan bulat [/b][br][br]Dalam operasi hitung bilangan bulat, ada beberapa aturan yang perlu diperhatikan. Bersumber dari [url=https://byjus.com/maths/integers/][i]Byjus[/i][/url], operasi hitung pada bilang bulat diantaranya :[br][b]- Penjumlahan [/b][br]Penjumlahan bilangan bulat dengan tanda atau jenis yang sama maka hasilnya sama seperti jenis bilangan yang ditambahkan. Jika bilangan cacah ditambah bilangan cacah maka hasilnya juga bilangan cacah. Sedangkan bilangan negatif ditambah negatif hasilnya akan bilangan negatif. [br]Untuk penjumlahan dengan dua jenis yang berbeda hasilnya merupakan hasil pengurangan dan jenisnya ditentukan dengan jenis bilangan yang paling besar. Jika bilangan yang lebih besar adalah[br]negatif maka hasil pengurangannya akan negatif. Sebaliknya jika bilangan yang besar adalah bilangan cacah maka hasil pengurangannya adalah bilangan cacah. [br][b]- Pengurangan[/b][br]Pengurangan bilangan bulat dengan tanda/jenis bilangan cacah maka hasilnya tergantung besar kecil angkanya. Jika bilangan didepan/dikiri lebih besar dari bilangan dibelakang/kanan maka hasilnya bilangan positif (cacah). Sedangkan jika sebaliknya, maka hasilnya negatif.[br]Untuk lebih jelasnya jika semua bilangan berbeda jenis dan bilangan negatif semua, [br][b]yuk kita belajar menggunakan geogebra yang sudah tersedia:)[/b][br][br][br]
PERKALIAN BILANGAN BULAT
Media Berbasis Komputer Perkalian Bilangan Bulat
Lembaran Kerja Peserta Didik (LKPD)Satuan Pendidikan : SMP [br]Mata Pelajaran : VII [br]Materi : Operasi Bilangan Bulat [br]Semester : Ganjil[br][br]Kompetensi Dasar[br]3.2 Menjelaskan dan melakukan operasi hitung bilangan bulat[br]4.2 Menyelesaikan masalah yang berkaitan dengan operasi bilangan bulat[br][br]Indikator[br]1. Menentukan operasi hitung bilangan bulat (perkalian)[br]2. Menyelesaikan masalah kontekstual yang berkaitan dengan operasi hitung bilangan bulat (perkalian)[br][br]Tujuan Pembelajaran[br]1. Menentukan hasil operasi penjumlahan bilangan bulat dengan menggunakan alat (geogebra classroom) yang disediakan dengan tepat [br]2. Menentukan hasil operasi penjumlahan bilangan bulat tanpa menggunakan media 3. Menyelesaikan masalah yang berkaitan dengan operasi pemgurangan bilangan bulat
Berikut Media yang akan digunakan
Selamat Mencoba
Untuk pemantapan materi ini mengerjakanlah soal berikut
selamat bekerja
-9×1=