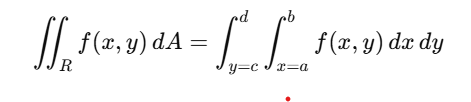
Introduction to Multiple Integration
[size=200][b][color=#ff7700]Multiple Integration[/color][/b][/size][br][br][justify]Through [b]multivariable calculus[/b] the concept of integration extends to functions having two or three variables with [b]double integrals[/b] and [b]triple integrals[/b] respectively. These integrals enable calculations to determine [i][color=#6d9eeb]areas[/color][/i] and [color=#6d9eeb][i]volumes[/i] [/color]and mass measurement as well as [i][color=#6d9eeb]center of mass[/color][/i] location and additional physical measurements for two-dimensional and three-dimensional regions.[br][br]A double integral serves as an extension of basic integration which applies to two-dimensional functions.[/justify][math]f\left(x,y\right)[/math]over a area [math]A[/math] or volume [math]V[/math] in space:
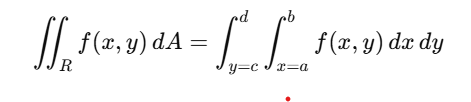
[justify]A triple integral serves as an extension of basic integration which applies to three-dimensional functions.[/justify][math]f\left(x,y,z\right)[/math] over a volume [math]V[/math] in space:
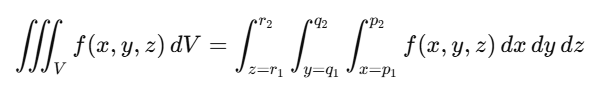
Triple Integral Formulas in Different Coordinate Systems

AR Tetrahedron
Tetrahedron
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAPIAAAA+CAYAAAARQkZrAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAcMSURBVHhe7Zw5ixVNFIZrvlxw+QcusYFO4hIouMaCgj9gcDARxBUxcgUNDFwCEwMdmWQCdVwCQU0UEQXBRA2NXBB/gPZT9rnfsaiee+8s2l28D5TVVV1VXdt7Tt17exz5WRGEEJ3mvzoWQnQYCVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQRY/z58+HkZGRgYJoFxKy6DE5ORk+fPgQ+K/O+4VhefbsWdizZ080AkuXLg3Hjx+v77SLL1++RIO2cuXK2NfR0dHw5s2b+m57kZBFhA387du3sHz58jpnftm4cWPYv39/NAJnzpwJp0+fbqVArl+/Hl69ehWeP38ePn/+HOeE/rYdCVlE2Li7d++uU/MPAt6wYUO83rVrV4wXLVoU44WGE8D4+HidmplDhw6FiYmJsGzZshiYE+q3nc4LmQXiCPTx48c6p71wXCO0kTt37oT169fXqRC9JXPLJrbjMGk891zB6x07dmzBvL+HfYFXXb16dZ0zOIz19u3b4eDBg3VOi6ksZWepjj4/lyxZwge2n7du3apz28ndu3d7fa0+h9a57WHFihVxPuH169exn5U36uVdvXo15u3bty+mZwvrNNc25oOnT5/G8dj4Usjftm1bnIsu0GmP/OjRo/gFSrUJw9TUVJ3bTvB4R44cidf0u03gfTkpcJSEHz9+xJjPsZY3NjYW47mcfDiyPnnyJFy+fLnO+TfgaQ8cOBDWrl3bG5+H+3v37g3nzp2blSf/J9SC7iTVQkSLWR3TstYVy08+lhUvSGxpA0+DNyKfOLXA1KMd86a5Mv2gX9QH+kxoE8wBYSbMS6cnH9KMLfXopL3nTT0xz8MrAvVsDf3agJ0E7BRDHdrmmVyb58zVtXw/39ZeGnxfqGdrTLoNJ4h+dFbILCwLChxbWQziFBMOx0QWi0WyBa8sbm9DAJuJtN+QfpGJSdPWMPhN3GR0/gbMmQnCw3iajBPl6T9znYrdNjkxY+I+18yvHx/XzCtlfPDzzjXrQb6H9m2d6Yt/HvVIk297wNoEK2dzb1Ce/NQogfXBB9svbaazQmYRmXSDjZIuGLAIXpwe8mnHsIVPN6zHG4JBwZDYBmvybDlym6op+LlI4dmIlXK5OWIecvjnM4acoTSYE9o2Yc0Gnpf2xYxwCn1C4LaujJE8L2QgL51rE/1s+9lGOitkFtwvBIud25BNwmtaeDaOF3fKsEK2Y6aHfg7r1ecCY2SuEBlj9kaNTZ0Tt4e6ZgiajJyJcCYj2I/c3OaeacbQGy/KpGOzNU5PGzmD0XU6KWSzqLmQCrNJeLbIueDLs4kRNnm5+/2grm/bh7+NjdkLgP4NcjoADFKTAGiDtnMnn0FJ+2b9Tdc0J1qMEUbYY+VSmvZEl+nkt9Y3btwI1SKxQr1QCS7em56ejvGgVJvkj3YI9+/fj/fu3bsXvxHfsWNHzONetQHivUG5cuVKqDzCH+1Xmz7eo/2ZGObdZ8r2gxcy6P/Zs2frnBB/J92yZUudmhm+2eY32Rz2q8G7d+9iPCz2lte6detiDDdv3oyxvUhiUJZ18d84P3z4MGzdurVO/ebx48fZ9Xrw4EHYvHlznSqEamN1Cqww3fbHagOLnB5jm6yvtZMe2zy5ujwj114OTg5pf8Ce3e9IuxDYaQYPyhymXgzwgHje1Lvm5hfwotThnveow5B6T47D9CHXP/L8RxPGQV3G5qF+2h87lqdlu07nPPLFixdjnHsrCAuNZ+YFfYPfBF+8eFGn/oeylZDC0aNHe+X5jZS3lyy9ePHi8P79+95vp9euXYuxb8+8Zo6TJ09m3+QyT8LvqvPxptQw7Ny5M3qzCxcuxHGkXszA8544caLXP8b+8uXLcOnSpZg2GMP379+j16wEFv/wgjqDvhKZgrclHD58OL4jALTnr+nHpk2bYho+ffpUX/3uDwHs9MB6pn+k8fbt29gW62flO00t6E5gX9YQUs/g7xGwvDOVBzwOZbDclMHSe0tNG9Tz97DwpM0jWDrF6hF4hsffa/rMuZDY51n6kX7+BOYFD8mYrZ/p3OROFbRl7TJ3w4BXtXmhTdrneaQ5AVl79gzfb8rSv9QD2xd01p5B2vpJeX+vq4zwTzUoMUu2b98e1qxZE06dOlXntB880apVq+L1169fYyy6jf76aQ5wJOuaiIGjPa+LNh2rRfeQRxaiAOSRhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIApCQhSgACVmIzhPCLwSPVxL+oefXAAAAAElFTkSuQmCC[/img][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAANoAAABWCAYAAACpb4h4AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAmkSURBVHhe7Z3JixQ/G8fjexfXkwcPLgdRUNxxAwUdEQ8KouJBBEVxwYPgjgdxQcWTuKMXwV1vjriAHlxwZwTFi4oIenL3D5i3P+l6xvzK6plq7co43d8PFOlKUtXTSb6V5MlTmW6tJZwQolD+l4RCiAKR0ISIgIQmRAQkNCEiIKEJEQEJTYgISGhCREBCEyICEpoQEZDQhIiAhCZEBCQ0ISIgoQkRAQlNiAhIaEJEQEITIgISmhARkNCEiICEJkQEJDQhIiChiYpcvXrVzZw503Xr1s0fq1atcp8/f05SRTVIaKIiBw4ccNOmTXNslNbS0uKOHDnibt68maSKatB2cyI39GrNzc1u1qxZSYzIi4QmOuTt27du//79rlevXm7Xrl1JrKgGDR1Fu+zbt88NHDjQ3bhxw/Xo0UNztD9EQmtAnj9/7gYNGuR69+7t7t696+MQEIYP4g3ybdiwwc/RLl++7I4fP+4uXbqUpIpqkNAakGPHjrmHDx/6nurgwYM+bvXq1W7v3r3u9evX/hw2btzoezTo3r27D8UfwhxNNCYlYbWWxNZ69OjR1ubm5iT2F8SNHj2aOXxraX7WunLlytZPnz4lqaIaZAxpYBg2Tp482ZUE5A4fPpzEiiLQ0LGB6devnw9nz57tQ1EcEloDc/LkST9Pe/HiRRIjikJCa1AYNmKunzFjhrt161YSK4pCQmtAMNvv3LnTm+6HDx/url+/7s378mUsDgmtwRgzZoxbtmyZO336tD+fN2+e9/gYPHiwmzJliuvTp4+PbwR44CxcuNCvJ+JexjoicUUgq6NoWFgjfPbsmTt06JA/HzdunB9KF2GB/Wd7NDwU7CkjRB7ojWgz586dS2Lah6EzeenFOWhz9O5FUDOh8SOtC+bYunVrkvJ7Wp6CwEMBi1hXgjmO/UYqLRyGpNNE7Xn16pUPhwwZ4sO8MC/FWwbWrVvnw5rD0LFW3Llzx3sRNDU1JTG/sDTCvHCfrHv9y/D3VvqdXfH31AN4wODhkoW1S/N8efPmTZJSW2o6dJw0aZLvhbIsVy9fvvRp5KlnlixZ4sMfP374MOTRo0dt6SIOjCr27Nnj515peP2H3q+kA/fkyRP35csXt2XLliS1ttR8jrZgwQL/R/MjQk6cOOHWr1+fnJXXcbCA2XAK60/6mjTkIW84b7MhWaU4CpqQcxvOZcWF8KBg6Btao/KavadPn+7DK1eu+NBgWwDgNzQyVrbpOgOGb8RbO+CcOqCOuI564jN5zNnZII4jnLJQ1iNGjHBfv351u3fvbstj8CYCztTcmzXFQil3bLUDR1Rue/bs2SSm1XfHxJlDqnXXOLMC6XTtOLiGTqtZQy2uS8dxbVYc9ys9ofw9W1pa/PCA+HRc6eGQXFWGe5GPv4t8WX9He9h3hzAs4XsbHcqA+mc4l25+lJGVG+2H9hG2Fas3wvS1We0OOCc+a0hI/VP3pHPwmbgiqLnQIN14KaTwnM/phmsFGhZUVgMnTzouKx/n6cZOHNenxRzmo6DJE3qzWyXmrQR+bzo/ZZLneq7Le3RlEBplEsIDKmwnYO0ijM8SqeVLCwpRpttBZ1CIeZ8u+/z588lZedi4ePHi5Mz5NDZ9CbG52/v3731YCypZ99KLsqXKST457yUB4b4YrK/Ahw8ffNgRNny0ezFsLFW298LoiFKd5D4qYUOkzjrygNvX2LFjk7MyTDmmTp2anJVhbg9r1qzxIbD2VRJlclbm/v373jQ/YMCAJKbM06dPf8vbGRQiNPMGp4ExrqYhd7UNXcKG07dvXx+X1/mWyqZyL1686M9PnTrlvTFikSXKmEceeAiFD1t703vo0KE+NG7fvu3LMjSiIci0cQPxpYULfM/IkSOTs86jEKFZD3Dv3j134cIF/75TVyOrAbHAmRcaghmF6MFxdcpDKPCOjq6KGZ8mTJjgQzhz5owP01ZpyhCjmUF58uCeOHFiElOGPU3SoyQTb/g9nUUhQmNoVhpT+wbGsXTp0iSlTPi0N6zwhw0b5sNKlOZUyadf5LUI5sG+P22JrJb58+f7EAsoD5q8PoRZAq90dFUePHjgQxMVZY0TQ3qIR70iqnDIzRIJ2MMcuB7LYlpQNuysdgG7CAoRGsyZM8cXUta4efv27f5JZavxPKUYWlHQ4RAT75C0iHr27OkLm8IlDXMu35POx3m4/wVYnjBvOo7vZz7F32NmZr4rXH7AtNxRj0Lj4D4MXfRiZTaUKwd7k9iyB/Vgn9nXBMaPH+9DCOfwPMSok58/fyYx5SWBtOcRHiPkC+swOqUnYyGUGr+3AqXNrQbxWIPIg/UJ025oDcTKRBoHaQaWO7sOiyHnZk20fIR2rVmrzBLIwfWV4oB7ht/P59BimGX1yoK/I7xvV8V+b96jI2gbVodW72bZtTqFrHImjfbC9WYZ5nrOiecag/jSw9vfg7BSW4yBvPf/ABZaR40a1TCbiTJHYgqQHpmI/BQ2dKxXGJY0ksgYyjH/kcj+DvVool1YosF6rK3A/w71aA0AvRJGAoaA+A5WYxDAZzM0pXMvenXzFeXgvmZKFxWgRxP1C8YDDAEYGUK3srxgZMgyUmFIAjNsYIgI84n/oh6tjqH3waWJHufatWtVe+dgeseNLVwD/Pbtm18XXLFihT9n7rZ8+XI/j7MXL8XvSGh1zLZt23y4Y8cOH1YLC8tz585NzsogWO1qXD0SWp3CPIz/0Env05FXCnmz5m34GYaLxZV49+6dd0z4Fzww/lUktDrF/gUuLzTiEWGGC4wYDAkBAwZppTmW/0eDafAf7OiNA+6FoOnl8rqZNSISWp3y/ft3H+LVvnnzZoxe3lUNt7TwTQLePKbXQyzM6QzM+uYKVQnycy+u7yhvoyOh1TmY4q1XwnDBdhL2VgFOvcQtWrTIp7MXv8HaGRuqtge9I4YWzdk6RkJrMOx9r48fP/oQEFxTU5PfxMbA5cpeYM0Ch16GihJZPiS0OqV///4+tE2BjEqvjqxdu9ab6OkB6e0wblSac7H4/fjx47ZtxYHvSW+YIwLKy2miHmGhmoNFZWBfDRaWK20SxMKzeblXymNvZYRvMwAL2aHnvPgvElodgyjC130QUntiQGCWD1FmwWstdr/0IaFVRk7Fog2siPxXGWAzUVE7NEcTbTAn27RpU+auvuLvUI8mRATUowkRAQlNiAhIaEJEQEITIgISmhARkNCEiICEJkQEJDQhIiChCREBCU2ICEhoQkRAQhMiAhKaEBGQ0ISIgIQmRAQkNCEiIKEJEQEJTYgISGhCFI5z/werk9J7YktpkwAAAABJRU5ErkJggg==[/img][br]where x is the edge length of the teterahedron.
[u][color=#0000ff]https://www.geogebra.org/classic/f8nsktju[/color][/u]
Introduction to Double Integration


Properties of Double Integrals
[size=100][size=150]Let [math]f[/math] and [math]g[/math] be continuos over a closed, bounded plane resgion, [math]R[/math], and let [math]c[/math][/size][/size] be a constant.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAh4AAABWCAYAAACAV59iAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAABQmSURBVHhe7Z3rqxVVH8fnPA+9rLy9iJKoNEgyCvMClUKBZiVRZGoUESTJyQiKyLALT2RmUQYSqZUgQWkXKYS0FBK6YWVSVPSijkRUr7Ss/oCe/Vmu32k5zXXvmdnbM98PrL1mr5lZ19+s9Vu3maG/O0RCCCGEEA3wH28LIYQQQtSOFA8hhBBCNIYUDyGEEEI0hhQPIYQQQjSGFA8hhBBCNIYUDyGEEEI0hhQPIYQQQjSGFA8hhBBCNIYUDyGEEEI0hhQPIYQQQjSGFA8hhBBCNIYUDyGEEEI0hhQPIYQQQjSGFA8hhBBCNIYUDyGEEEI0hhQPIYQQQjSGFA8hhBBCNIYUDyGEEEI0hhQPIYQQQjSGFA8hhBBCNIYUDyGEEEI0hhQPIVrMU089FU2YMCEaGhqK7rzzTu/6Dw8++GDmeSHKIpkTUjyEaClU8AcPHox+++23aPXq1dGhQ4f8mWNQ6f/++++p54Uoi2ROwNDfHfyxEKIlfPXVV9FFF10UjYyMROecc453/YePPvoomjt3bnT48OFo4sSJ3lWI7pHMCUOKhxAthJ4lvcl3333XuxzPsmXLnL19+3ZnC9ErkjlhaKpFiBZC5X7xxRf7f//mtddei2bMmOH/CdE7kjlhSPEQomUw5M08+plnnuldjochb5g+fbqzhegVyZwIkeIhRMv47rvvnH3++ec7O84nn3zi7FNOOcXZQvSKZE6ESPEQomX89NNP/iiZH3/80dknn3yys4XoFcmcCJHiIUTLeP/99519+umnOzuObWG88MILnS1Er0jmRIgUDyFaStKWRvjhhx/8kRDVIpkToO20QrQM3ggJaY9+3nkhyiKZEyEa8RBCjHLkyBFnT5kyxdlC1I1krn1I8RCFoHJgy5tVEv2ALXmYEwHmrG2L4CBhc+lplbztPpg6daqzBwnizkuo7EVT/WDz5s0u/EEs20FlUGVO8tQ/pHiITBYuXOiGQSdNmuReZ2yVRBH4GBT3Yrp9sLjP/OB1y6tWrfJnBhOLK5Us+TVo/Prrr84eFMUCRZKK1/INeUuCl08tWLDALT7s55stV6xYEd11113RPffc4xqtMoSyPGvWLO869mlS5ugYUS72kTlMEmNBnsDSiOlnp7AstSkeaHLWaIUmrWIRg8krr7zS1yHQyy67LNq0aZP/N/h8+eWX/ujE5M8///RH9YPScfnll7u3VTK3v3Tp0sQ3W9Jg33TTTdHWrVtdRd1vkEle+71nzx730bOicJ/JB41eHvhNnTnWe8NVyRwNL+0LH5j7/vvvXb0xc+ZMf/Yfxoo8Ad+1oX4mnXnft9m1a5eTJzqEfafzwFdKJyP+7mQCK4ScPTIy4tw7QuDcrrzySvd/kCBemA8//NC7NAPhWdiDDGWWlkd27sknn/Qu1RPm0yDKTxyLK2bQeOeddzLzkXJsKp8Jo1Np+n/JUJ9wzfDwsHcZHEwuy9QbHcXD3UM5ZGHXlfV/EGlK5swfa3OSGGvyBOPHj/979erV/l8ylm78r7OuLkrlIx4333xzdODAgaiTGU6Ls+1TaJb0aAaNfml/aOfPPfec/3diQs/hvffe8//EicA333zjj7JJ2/ZYFcyvIzt5Pf+9e/e6r5ned9993mVwoKdKT3PNmjXeJZ9ffvnF2eedd56z02BK0erLn3/+2dknKk3J3AsvvOB6/1n+jDV5oh3hVfQXXHCBd0lmy5Yto6M/9rK2flKp4hE2RMzbxod+mEuLf5mQe8I5XubmmOuKLyK082aA6Ryby2OILT7HZYuHmFu0+8KFPNwTrhlgTt6us2sYnsIP5mTtHP7FFRY7Zway4seaCT6KZMTvjcP94TXEj7hZ2kL/iVtauKEfnAP8SnLPgjDCNQzko93PuaT4QjwshhYpJ7ue9JBvZYivE8AP/I3LQwhxtOsx/MefMN4QXtNLfhnEKZyDxibutgBvUDjrrLP8UT08/fTTzp43b56z03jmmWdchVm3ItQtN954o6vzsmQthEY4r3GknsQ/5v4h762fY4VeZI48Q6HIU2THmjzZmrvZs2c7OwnqlnXr1kVr164d/d93/MhHJTDcg5eYIsM5NgSHseElhsD4z/ARw40Gw2e42fV2XWjC4TOGluz6Ts/BueGfuRk2PIeJD3HZOYsLfjIcmHR92fhB6Fce8bDT/M8LNxzCDYc2t23blugOaWnm2Nzj5Z2VVzbthkFmbAgwNOFQdBhOPG5xGSLcTsWSeG2cUF6RkbD8MNBNfpk7JiSUEcsvKy/ciXvdmEzHy8vIO58HaSRNYV6Gw8BhfobGntE4nAvlNySUsbAMCAOZIg5F4HrzJx6WuWOSMNlMmjrBX9Jl9+M3spmWViBNxBt/ze9uy6Iq8so0j7plLoyXmbSy51yaPIHVCcgP6YZQzijTPLieMLie8g6fa0srhvKNkyVP5q+llzhZvZUF11ne2n39ptIRjy+++MIfRdEll1zij9K55ZZbnN3JTDfMBI899pizGT564okn3DGgoca1uk5BRJ2C8v+i6PPPP/dHxzRB/IDrrrvO2axgfuCBB9xxGYgf9zKCc9ttt3nXfz5sBGXjVxbCvuKKK/y/Y351HozjFjNu3LjR2Vnhpr2SePLkyf6oGuLxDQk/FEWcWeTVkcWo89B71yh6+eWX/VE2d999t7M7D6CTIcJdvny5c6PnEB85C7nqqqv8UeSmBzHkZ+dB9q7V5he9fGQS/++//37nZovbcH/zzTfdMdjIi40UNYW92robyGt6kyzuIy+RQ3r3yKlBflLWlBf5wDEmaWeBpT2tJ7x+/fqoU6G6RYRW1vTmGH379NNPXTyKwPUsouY5Rx7DHiHu0KmsnZ1GfDqBuLNwFkg/aQTyxdyTIE302pHltNeLpxGO1hUxRWSrSJn2Si8yB8TNFqDz/JLXSWWfJ0/IIFMW+EH6mJYBlg8gZ/ibVh+EPPzww+657nROXJ6ZP8BzT34i+9OmTfOu/yYuT4yAzJkzx9XlO3fudHGhLWLUPGuUh1Fx3gp7++23u/+U3SDQt+20CIEpBqEg0HDYQx5ORcR5/vnn3bWmsACFnARD2yZ0FLxVAnnYtY8//rh3Kd7glIlfNzz77LNO2eFBCCtFFLc6w60alDWL67333utsyCp7gzK1CpCdEUao2NjUXx533HHHaH5SaRWVkTKYYhgqqGFF9tZbb/mj+ui1kk+DipEGlYqNCpy8RA6Z9grLxmAFf5GdHVnwXJJ/8+fPd/9ff/1196zTSBB2UZj+5fpFixa5/5999pmzwfx56KGHnF0E8uLaa689Li/A/E/7QiuNPDJiQ+J238GDB52dB+lAbouasI5IomyZplGXzIXs27fPNeZFFIM0mPLE4Adp5nlEnmjgy/hL3R/K5QcffOBsgzykA1xGRlF+qJeoF63czP+0sqD86Jht2LBhNCzKLpTvftE3xSMcLagDCoceDKDgsB6BHgEaYBkoPB46BJJCG8R3M4SUEeZBg7jTGyhKKEPhGpNBLKOwd4kyFPY8k7BGJK9xGBQYreE5e/TRR73LMUiHje4YNLBcW6bxyoIGkYaCBpuKttvGxxZ8fv31184G6gsU+zLlkJYX1otN8wsZpkEyhcM4evSoP2qWMmXab1Bks9Y5lAWlmOcUZYa6vxuoz5DLcMSZ9oSG30YgisDzQlxoz0LZsPUdabMLLCilzbr66qu9yzEo035TqeIxbtw4fxRF3377rT/qH2ieDHdR+EDhXXPNNYX3SlPg5557rtvzDTt27DhuCkNUT7eKkw2Fxs2gVZBAQ5YUVyr0QeHUU0/1R8Wgd0glHa/kkti/f7+zi0zHFsWGr4uEn4YpMOGUMb3FMqMdkJYXb7zxRuqUDZ0b6qdQgU5TSpuiTJlWQVmZM0yRTZva7QZTXpcsWeLsbkGBCUecUQbKjnYgFxCPy+7du52dpMjalCP3hvJkfvWbShWPcO4ybyV2kUoHoe8VtFXmuGwOEGwoM05829oNN9zgBJrKiIqh255UEfqx0rjKL0JWtUWLHgGYspjF9OnT/VEzW8R6ya9wPvdE+BJn2nRAGlRoRXucDItD3iiCnc8rWxoeerw8qxz3AgqMDUUzSoUykhVPe/lVKItJecHzTQOU9II0ZJ4hfeqouDJahqrXeJQp0yooK3NGUUW2qDxRHi+99JI7Nr+7xdoM5BJ/UT6zOkNJ8mRTVfH2h2mXtBFi5Il1VHF5SlN8m6ZSxWPx4sWjygJzldaIGCgBtvWQitiujc9h2oPf7RAXsD2SYSaDxT55mf722287m0JDUGz9QOhPXXvqWYBEfln+NAHpswfi1Vdf9a7dQcWPPyhoZbfDGtxvvYMi8/8stjKQN8I2GCJnC3SVCl0v+RVOI+FPuN0XP7uZBuyFtEq6CaUIWSlaAZJnWYuyyUMWE7PgDnptKJj+saFo3qdgi93T+Pjjj52d9V4O4mjbhy+99FJnh7CglG3VSW/RJJ+K9lKrXuNRNXXJXFFFFvLkCVauXOnW0NE+md/dYsrUX3/95coZf7MoIk9go/ZJ9ST1CDKT1MG2UaE8pbN2OgJYKeE2w+Hh4dGtRLaFsvMguf8QXmvbh9j2w/9OoY9uZwKOcbPrbVsTtrmF7uYPcQDi0elFO7cwDvH7MR3hdNdj89/igmH7kl3HsaWvbPzA8iQ0Ft84hEO87TruNXdLF4btWJAVbpgGM5ZfGNJtxP23cI0wzRj+E1Y8vuH2O+IYvx5Iu7mFZR/mE3GxPIcw3nGTlpeGbZ3DhDIRp0x+ZeV7mO64MZkzLO+sPKsiz1+LT9lwyaOwLCk/8p98CrH8Kbod0+qIUB4MkzELk/D5j3v4bIKlOw8rI8ojaUtjHOQRv0MsL4iz5YOlAz8Jw9Jv4cXzCbiXc5gwLU1RtEzzqEvmDOIYPoNZZMkTWFmBpZ+8xz18lu35LxJnriN+RWQ+SZ6s/kN2iAthc4wbfpIW4gqct+cgDueIh/nVTypXPIACoqDCBstMPEPIABNMDPdwb/xBC68xA3E3c+d+CswyGoPfFFrcbwSNwuIawrHzpMPC5bzda/5h7CEsGz8jbPyyBNMEPTQIfVq4ae4Qpos8sQctvNYEOcmf8GHDLytnbHs40+IL2OZGvlreYxNuWCmE15ohTiHEPyxnji1NaST5a2UZp0x+hW5mQgiXa+1cmkxaeJZnVWF5neavxatsuMQ/TFdaGYSVaBHwlzyiTgghf0hL6A/h4Xcoh4blZx7W2MfDS8JkKJ5X4TNh8mzpML/5z32h7Mf9wd2MyVeTFC3TPOqSOSCvubdIow5p8mT1VVgH4Ddxx8TTbdcXiTPhkXeEnQV+JfnJfSa/+GPnrWw4R1yRM87jhol3Es0P8yesZ5sm/0kUomLsAcPwMIjmsHxPqzDtfF1YZZlXCYeYvPTSS0POaADyoAIv0khYA1a0wWszJlN1yFxZRRaqkCdTPPIab+QEeUKusmibPEnxEI0jxaN/WL6nkXe+V+g9dlPm9Di5N96LKwKVOvfmNTRcR9zyGhPkN6nXLJKpU+ZQZClbyq4MvcgTICdFlARkJE/u2ihPUjxE41gvBcMDV7bSEN2TVclTDlnne6XM8HQSKARUzmUraMJNmyLAnQYEv2lM8nqmyC6NXbdpaCN1yZx1YMLpkTJ0K0+Em3YPftqIGdekyZ3RVnmS4iEaxSqL0GjUoznIb3p6SVjZVF0e1rigZPYyvF0HNA7Ejco/b6RDdEcdMkfjjp/dKh11gaJBeohf25SJMgzx08koIcQYhy10vNW1U8knvqws77wQZZHMiST69sp0IcRgEn9ltxB1I5lrF1I8hGgZaa+WtpfjpX29U4hukcyJECkeQrQEq+TTvolhnzkIX9csRC9I5kQSUjyEaAlWyed9E+OMM87wR0L0hmROJCHFQ4iW8Mcffzg77ZsW9s2kOj+GKNqFZE4kIcVDiJbA595npnzNEo4ePep2FwhRFZI5kYQUDyFaAl99zvrqL1+0vP766/0/IXpHMieSkOIhRAvg0/t87n3JkiXe5XjsM9nz5893thC9IpkTaUjxEKIF0LNkSDttLn337t3R8PCw3qcgKkMyJ9L47/86+GMhxBhi1qxZfBIhOvvss10F/+KLL0annXaaPxtFEyZMiMaNGxeddNJJ0SOPPBJt3LgxGj9+vD8rRHkkc6IIemW6EGOUqVOnRiMjI9GUKVOirVu3/mtnQXh+x44d2lkgekYyJ4ogxUMIIYQQjaE1HkIIIYRoDCkeQgghhGgMKR5CtIRly5ZFQ0NDxxncjhw54q8Qolo2b978L5ljASpbbUV7keIhREvYvn27s7dt2+Z2HrDI78CBA9H69euduxBVs2LFCrellh0uyNzhw4fdwtLly5f7K0QbkeIhREuwXqa9sIn3J7DLgJc8CVEXvL100aJF7njixInRjBkzJHMtR4qHEC1h//797rsZVP5MrzAMTqNAr1SIOrC3l86ZM8f937VrV7Ru3bpozZo17r9oJ1I8hGgJ+/btc1MrzLNPmjTJNQr817sURF2g7ALyhtxt2LAh2rlzp1tbJNqLFA8hWsKePXtG13csXbo0OnTokF5XLWoFZdfWd2zatMmNsE2bNs2fFW1FiocQLcCGvGfPnu3+33rrre5bGigfQtQFyu68efPc8eLFi50M7t271/0X7UWKhxAtACUDbITD5ty3bNnibCGqhq/PomhMnjzZ/WdtEWuMeJW6tnC3GykeQoxxaABWrVrljhcuXOhsawTWrl3rFpkKUTVz5849zoYFCxY4JXjlypXeRbQRfatFCCGEEI2hEQ8hhBBCNIYUDyGEEEI0hhQPIYQQQjSGFA8hhBBCNIYUDyGEEEI0hhQPIYQQQjSGFA8hhBBCNIYUDyGEEEI0RBT9H7PAcZhafhv7AAAAAElFTkSuQmCC[/img][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAe8AAABDCAYAAAC1II3sAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAABNCSURBVHhe7Z3byxXV/8fH333FV7uqiEgDIyOpzMi6CazILgosi7oICiqLoJIOWhdRWEoHiCiVAm+i7IAhpB0gISvsJEVJF6VERFePHewP6Ldfy3k/flzPzN6zj8/e9n7B2jN7zcyatdbns9ZnnWZmzr8tCmOMMcZMDP9Xbo0xxhgzIdh4G2OMMROGjbcxxhgzYdh4G2OMMROGjbcxZtbYuHFjMXfu3GLOnDnF6tWrS9+jrFu3ru1xY/6r2HgbY2YFDPO+ffuKP/74o1i7dm1x8ODB8sgRMNZ//vln7XFj/sv4UTFjzMj57rvvisWLFxcHDhwozjzzzNL3KJ9++mlx2WWXFVNTU8W8efNKX2OMsPE2xowcetX0pN9///3S51huvPHGtH3jjTfS1hhzLB42N8aMHIzyBRdcUP6bybZt24rzzz+//GeMybHxNsaMFIbMmcs+/fTTS59jYcgcFi1alLbGmJnYeBtjRsqPP/6Ytuecc07a5nz++edpe+KJJ6atMWYmNt7GmJHy66+/lnvV/PLLL2l7wgknpK0xZiY23saYkfLxxx+n7SmnnJK2OXok7LzzzktbY8xMbLyNMbNC1SNi8PPPP5d7xpg6/KiYMWak8LY0qKt6Oh03xrjnbYwZIw4dOpS28+fPT1tjTDVjY7wptDwiosLbBM73KxNnh17kNWjGIQ6mO1Re64yzVqIvWLAgbc3kgqx5GY9euDNbbN68OcVBjyAeL8y68b7qqqvSMNnJJ5+cXoeowlsHHzLgfBznv/322+WRIyg8Db01pdfrIjFux5uiiG7lNQzGIQ6jQvpEmo8Hfv/997QdhHGmjCl/5OrKHQ08DIk+coKrgzCo7CnPs8WkGxxewnPFFVekRYez/Za8O+64o7jnnnuK++67r/LjNrHuxzWVe6zveU//qBmY8Y4ZwEsYmvLaa68VF154YfmvMw8++GBx1113lf/MqOlWXlSaVERLliyZ1o/oeqHbOJjJ4fDhw+VeczZs2JDmx3GXXnpp6XsUdJD6iQ+c/PTTT8WmTZtq9YdK+NZbb02VPXXNbNHJ4HSDjMyooMFx0003FVu3bk3pGAfQC17F++GHH84wtPhLf7oB/UCXYNmyZWnbDtWBg2IgxpvhkQ8++KD8VxRvvvlmudcZPjrQ7YcHzjjjjHJvJu0EIYNR1ZrtVYARhKkw8kpEjZvZbM0Pgm7lRbrvvPPOtM9HKMibPXv2pP+9wv2vv/768l9zxlEGqliJWxXSp7p3gE8anYzzDz/8UO4NjldffbX4+uuvi/Xr1yfdwaB89dVX5dGjIIuXX365+OKLLyobAaOmncEZV2go0fihgzUOeRhB9jQo0INBj2gsXbq03KuGDgw6OEgGYrwpHP/73//Kf0feSzxuzGaFjaLExs1/BYbLpLCPP/749KNBFOpRj56Mowxo9G7ZsqX899+gqXGue4ysF8hj5tjbhclo4UMPPVS89NJLXTVOh80wDc4w+Oijj1Ijfc2aNaXPeEHdw6jLk08+Wfr0By8cQrfa6QwNmkceeaRYtWpV+j+odVoDMd60VqmMtQgF4dVFUIsYNPfE9ssvvyyPzoSEY3iZI+N8XF2Fp+Nygl4NBVMwT6pzKBDxGpzI/XUsv4b4qVcnp4LGMe4niIfOya+RH3Bd9K8ruFQ6tMpjWOQpeUzeiar44ZSvbKumO7qVVyS+SSuvtKkk6VFCXVrr8rSKnTt3TqeF62Ja2smgTnZ5eEBe0ILmv/IDx9xkVd5V6a7mMXGUF8oK0LDQOYTPcf2XXw7nEJ7OkdxjXKrCIV7ojPzGsVfXbnStG2hAksfMv7YDuSIP8nPcGLTBGSbPPvtsiusgG1+DhlE7ylusH3vlm2++6ahbjz32WLKP+tCO1n30TasC7YvXX3+dGvjfb7/99t9WBNM+btOmTeUZR+GcVg89Hd+wYcMMP9yePXuSP0xNTf3bUoTk32q1pP/RL4YDrUJ6TFgRzpN/vAfUXUfc5Ifjv1i7dm3yIy6K15VXXjl9brwH+/KP8QXyScdalUcKRyid5GsVMVzkAIoXLt4rj1+UlRz3j3Qrr5yYthhGFcg3DzOXdbxXlGdVWohjzMt2MuiUNxyDeBzee++9GeeIGHfdT2mM59ZdD+3Cj8eUL4o3aY+6Gs8lTjFP5aQ/w0Zyq9OFTscjkmnduVFP5fDLQVYco+zUoXJFGaG+gKg3Mb/r4HzJCBnwXyjduKjnQsfjNU3Rtf2guCtPiT86k+cnx1Q+qiCfyEPOi3JTWJSRJhCO8j6/n/xxVUhvKBc5ebwinK+yQ1yVr1W2TnAvziX/dH6VfHuh7543QzqtBKVVhddcc03pWxSvvPJKuXeUp556Kn1NiBauFoNw3UUXXZT2c1hJrmFXzVfh6uY7ae3VhdWOuuuIm4Y6ck466aS0ff7556fjdfnllye/bmD+rSXctM+Cmjj8wj7HnnjiidKnGvJfPYbbbrstbUGvoYQ8fsz50SNpKdX0/fkfW6Pdyitn5cqVx0yn0OOlF1q1+rTq84/K107EtJAXQLwZwmtCnjfIgbBaFUrpcyySx9VXXz092pQPydPaRndj3rEAqRsIv45bbrklbVsV1/TcouJF2pGdiOEQp9tvv51aLS30Et9//325dwT1ykdN1Nl+QY5aUNSq7FOa8cvR0wrnnntu2uagrxwjDPRMenXzzTdPL5ajXHQCnaC8o1fIIeonOoLuUl7OPvvs0vcol1xySdoyHz9qGHE666yzUjnbsWNHSi86xKI06T8wygPtRk3QS9JAvfr0008nP0a5PvnkkySbpivTqUtYuIr+M/IbR3rxh5YRT9s6ullfwcjMihUrku2hbmDh41tvvZWOXXzxxWlbBQsOSTN1TN1X9HqlL+NNhlFpIUjIK4mYoaC5cCrwJmzfvr3cG+wcWDdce+215V5R7N27t9w7UsmgHINYlCHDS6WrIU+MKMPTDz/8cK0B494UpLj4pmk+0ejgXMKOxjg+dtWtvHIIe/fu3dMGFaj8KPSkeRDDVhDT8sADD5S+nT+AUQdGlrCII/mrxWLs46I86vKGCgXiccmr38VnVJLoCsSKknipwqpbd8JxrQCWQQCG/0bBII1zE9A/DGI746qvmJ122mlpm4Me4AgDY0W9xPQEC7OaGG3BVBHnL1++PP3HYEWQX7vyDp0MDtMianjJacow98fJ4LaDtAJ6q/pOX4TrNGScg3EmfdSr6DBG8YUXXujYQckhLoSjDmOcylP+Pfroo2nbL+QRi27Xrl2bGlmEj1Pa63SAtIHKm/Rr//79adsvfRlvFqqBlBFiTzVmaBMlyRmHBUYxbRpNwMASt3vvvTf975c4YvFmuVKfVjnKHXvSddBypYAN8lGEXuRVBYpN44LeRmylY1yee+658t/giBXwvn37yr3BgezjGoMqHa2a/x4kMjbDRA2VSYeV2r2MxtVBhY3MaRCo0d0tVPyUhdjoVmO9SXlvB0ZNspPTCEvuj+vU+aAeIL11jYomj0hVIZmwkKufRYILFy5M2zhyRH04qI4VvPjii2l7//33p62gwVvXu0eepI2ORc7ff/9d7vVHX8ZbvQsUUS252OJ/9913y73JBaViaAY0mqDFLe2GNbshDr8q/1j4wX3bKTUKgsFmOIeKgBXdFMhxhIqO4TLlJUh/hgULuAYJDaTFixeneNPrYvisqvD+888/5Z7pFU1L9QONKBrAvUxn1aFe1g033JC2vUIjgPpE0BHq1OueDXbt2pW2uZ7Lv9MjUnUwUkYDiHzoZ1SVa6k748gRPflB9bqBOplOaZQNdS+NmjrdYooE3YuLo+Oi2UHQs/Fm+IPI0aOKLTmGRQWJ1tBonMdp+tWgONyaD8H3w2+//VbuNSP2jClkpL3XlZ/6VnGORizIPxoHFOxOj1toXhXI60E1JqAXeXUC5aeVLdCfKrqVTx11c291MmgHMldjgzTQGKmraHvJu27yOA531xHXGkwiGpbtB01zNcmvJlCXafQtTqH1ghoBNDAIl/lTrY0YJ2QU49Aw8aW+wWjGMqCebpPypSFlRkb6BTuhUV5GCjDo7XrdetfAokWL0rYdGoHM1+RovUJVGFxDXaF1FnJ7+ny/RU7PxpuFapAPHZFx0egqkQhZvUsMlBYmkNA4vB6hVymeeeaZtMWIa6FAr2hEIH+spg6MoipDFs7Ro+t1yAxlRflJvxQYYkue+RWMeacWaWzQ6NxBNXJ6kVcOQ8tVjziJqCcRyafpveKLP+J8Ut2QVp0M2hHnz+PQfJXRJe+UNvKOx8WAe7KvOcQI56GLuKrjERoH0sd8akD51at+joo6gzqohiIw3w2dhk8Vl06NxrvvvjsNg5L3CrtX1DhhlIbpo6rh1Ug3BmfYEF/0tWq+G72P0wFVoOOsG9CC2CZ1cDswrOoI0KnqNH/+2Wefpa2G3LuF+Mr+VY08sEiNEcZ8Llx6OLB1H60WQdewrJ9LcVPZowv8bwlw+jj7OkdL5aNrFYTpxydwcfm+lvTnLj4OFR/vaClUCk/HYlg8WiB/OcWt3XUixpF05BBOy1hMn5M/dhLDx/GfOEVaxnL6eJPHCWI+EGfiQDwVDlvSBnn89HgD/vG+8bGHbuWVo/vFMNnXtTGNVfLhXnkaRYxbq6EzLUelhTjm1Mkgz5sq+XJvHZdsOS/qekxPne7iKD+CuNcdj/ckrpIlxDKofFGe5OfGcMgf0gtRFtEf5D9olM91+q37NtF/5XGVvIB8QD6dIN2Ek5fZCPokuSAzwuY6/GM5lgyaxJ/ziF+7+wqVgyjXpihOvaD7okNKr/QmlmshvayLJ3mFDhCWyjzxYz8vsxzj3E5ID8hLlYV2oOt14So+EWStOHMv4qk8xY98kG60k7/ypolONqFriSqjoouocEYXM4rEkRn4UwgQshKM41gsDAhDFTKJ5v55HJRxVfeOcJ7uLWFAp+tAiqZCmxPTIBcFyPVKB9uYRqFCEfOrHcQDRdL92Cc/Y3oUVl38qtIe492tvCJVYXM+8ay6Jr8X6cvjrevIK4WFXug4ecs1VdTJIL8HLuaBiPEjbZyTXxvheDTOuiZCGpVPhC1dBl0Xr49QNmIekybyI9fPGAZO8ajyF/IbNMq/qvwF3bfueERpqJI3suVYE8MI5Bv5lyP5xnsQNunI5QU6v0n8uR+6W1Wf5HBuLv+mKE69EPVT9a8agyo/Ec6XHkbwJ78II17HeYTFPar0tkmaqZM4N79nFdKZOvlwLNcn2Q0c+kQ8uV5+Ol/1N450xgaM7itX1fDplsGXTtMzCBtlyCsEY44XVHm1qzxxTVCFmFe2oIq0SU8MZOz7LXsylLHirgIDkBuyOpTOujwbBsQPw1kVP4wk9VQdim/TvK+DMJoYZOLYpBHEcRoW7Rp03LNKn8YRG+9ZRkpOYUcBccYcr6DvuDo6HY+0M95xaLsphMM1nQxvOzB4TXr7GKUmxq2JwYmol9zU1TUIiB/3zVEjp5OBU2+11x4m8WoiCzUyOp1HeFUjAjlN0jYu2HjPMrEg4Zq0xI2ZVKTnVVARtzueU2e82xn1TmAkMRp1Rq0dXFNnHNQ4J42c06SH39TgDAPuSR7GfKCxQd406eUCaSacXuJP46uuLiTvkBPh140ORGhAEF4TmfaqN7OBjfcso0JCIe2lwjBmkkDXMQBVoP8cp0Jugs6PbuHChSn8fipgwqWyH8S8pMDgED8MX5Ny3o3BGQZqZFAvKW/ZJ1+bGO5hojqT/OnU425CPloxKcZ7Dj+tCBtjzFDh0T9eVNGqLCtfEdvpuDHmKH29Yc0YYwZNp/cbGGNsvI0xI6bulZJ6ScqgvuVtzPGMjbcxZiTIONe9t1xvsRuHt4gZM+7YeBtjRoKMc6f3lp966qnlnjGmDhtvY8xI0KcQ6941rve05++ENsbMxMbbGDMS+ELVhTUfo4G//vqr9mMyxphjsfE2xowEvnhW9SUqwfeRr7vuuvKfMaYdNt7GmKHDZxT5bGP89G2EZ7xh+fLlaWuMaY+NtzFm6NCrZki8bj57165d6RvIfsbbmGbYeBtjhsKSJUuKzZs3F4cOHSq2bNlSbNiwoTxyhLlz56bj9Mq3bdtWrFmzpjxijOmEX49qjBkKCxYsKA4cOFDMnz+/2Lp164xV5vH4O++841XmxnSBjbcxxhgzYXjY3BhjjJkwbLyNMcaYCcPG2xgzEligNmfOnGnH/3Xr1pVHjTHdYONtjBkJO3bsSFsWqbHUhv/r168vdu7cmfyNMc2x8TbGjIT9+/en16PqWW6tPj98+HDaGmOaY+NtjBkJu3fvnn496sGDB4vVq1cnY+63qhnTPX5UzBgzEpjj5hWpYtOmTcXKlSuLefPmlT7GmKa4522MGTp6tznz3VNTU+nFLHwi1IbbmN6w8TbGDJ29e/cmg818NwZ71apV6ZWpxpjesPE2xgyd7du3p9ehimXLlqVeuFeaG9MbNt7GmKGycePG9FUxHPuwdOnStF2xYkUaUjfGdIcXrBljjDEThnvexhhjzIRh422MMcZMGDbexhhjzIRh422MMcZMGDbexhhjzIRh422MMcZMFEXx/+gkYYgRBb+cAAAAAElFTkSuQmCC[/img][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAASkAAABRCAYAAACOn1CaAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAxtSURBVHhe7Z3ZixXHF8fb37uGqE8aJDg+KCqKMSpuoOCC+qAPOtFIECK4IIIL7j4ZV1xAxA0FEcREHwTBNaDghiYqig4KLoiIT+P6D/ibz7FP7Gl7u/eOd6q7zwd6qrt6mb5d3z5VdWrpDp9a8AzDMBzlf35oGIbhJGakDMNwGjNShmE4jRkpwzCcxoyUYRhOY0bKMAynMSNlGIbTmJEyDMNpzEgZhuE0ZqQMw3AaM1KGYTiNGSnDMJzGjJRhGE5jRsowDKcxI2UYhtOYkTIMw2nMSBmG4TS5M1Lbtm3zOnfu7HXo0MFbuHChH/uFtWvXJu43ioXpofjkykghuLt373pv37711qxZ4z1//tzf8xlE+O7du9j9RrEwPZSD3Mxxfv/+fW/gwIHes2fPvJ49e/qxX7h27Zo3atQor7m52evSpYsfaxQV00N5yI2RIlckJzx//rwf05pffvlFwj///FNCo9iYHspDbqp7iO2nn37yt77mr7/+8gYNGuRvGUXH9FAecmGkKNrjW+jRo4cf0xqK9tCvXz8JjWJjeigXuTBSjx49krBv374Shrlx44aEnTp1ktAoNqaHcpELI/Xy5Ut/LZoXL15I2LFjRwmNYmN6KBe5MFKXLl2SsFu3bhKG0ablAQMGSGgUG9NDuciN4xyimprh6dOn/ppRJkwP5SAXXRDoLQxxt5q23ygWpodykauSVBRv3ryRsKGhQUKj3JgeiofzRkr9C3Gi05aeXr16SVgPuCc6E2qHwfbiwIEDcg/a5F4GXNQDuKCJourBeSP1+vVrCeshOvrfkMhUF1gmTpzo7/kCnQjHjx8vTtn27s08b948b9GiRd6SJUvkBakEBubq72QMXF6opx6y4oomatEDuKqJ3Ff3Pn786K/VBgZqzJgx0ksZX0ZjY+NXPZrJoWbOnOkdOXJEBOECI0eOlKEhFy9erEhYK1as8Pbv3y/rI0aMkDCJn3/+WcRbLRj8KKPf1rSVHrLimiaq1QPUWxNZcd5IpYnu4cOH/lptrFy5Uqb0IKGAHHHjxo2yDvg65syZ4y1YsECE4BIMoOUl2bRpU1VF/aFDh/pr0VCNuH37tr/VvtRLD1lwVRO16gFc0oTzRiqr6OKao7OAP+HChQtSZI/j77//lhH3y5cv92Pcgpdk8ODB3h9//OHHpEOnSHw7SbME8CKuXr1aSpagPqH2oh56yIrLmqhGD+CiJnJf3VN+/PFHf61ytm/fLuHo0aMljGLHjh2S6PUQf7VMnz5djK22cKVx586dRMMM69evl5KCDtZVn5Dr1KKHrLiuiUr1AC5qIjdGauzYsf5a24Efijr1vn37ZBvfAttRLTQUbamDx4EQ8LlwftD3wv/AyUtVMgscr9cJOz81niWK4cOHS3jr1i0Jg5w9e/Y/HwL3gpMUASf1yqaqQLV36dKlfow7fAs9KOEGFNap3oR9amma0LTnGjxvhWdKGkTpLArSTq8TdszrPYbvDZL0AHnRRE1GSh9Q1uVboEMkqoHEUCf5999/L+ssYSFovT4pd965c6e3detWcTyS0AiUYjC+LkTC7JBZ4Phjx45JToXxDBaliYcJEyZIGEe4SsQLNnnyZMlZmQTuyZMn3smTJ2XfsGHDJIyCVqLNmzdL0T9uxgHXqEUPwIvLZHpAVU47hM6fP79VQ0oWTfDsSHv0tWXLFonj+leuXBE9hHUWBel/9OhR6UVPNWzdunX+ns+cOXNGwiSjHVVFzpMmajJS+lJnXaqhVtFlgZaQtCJuGjjZMXrjxo2T7RMnTkhJCMOVVL8PQ8sMx0+ZMkW2//nnHwlBrxMWahK8TLxgTJ9LowDXYNHfG5drImLQFqsffvhBwqamJgmTiMqgMNwsUfsq4VvqgdLw7NmzJRPAgGg1Tqs1WVq8gnANnvXUqVNlahme6e7du70NGzb4R6TDPagxw9hhOIMZFzM9kMH+/vvvfkw67aGJWiiMT6paKPEgoLaaIA1RkePRsrJ48eLEonMSvXv3lvDBgwcSArkwL1AlLUl79uyRMFw8x/cQVyJTx+iuXbv8mC98+PDBX4snKoPif7FE7XOFw4cPixbiMoG0Fq84hgwZIiHPdO/evWIQqqF///4SPn78WEI4d+6ct2rVqoqu2R6aqIXCGKnvvvvOX6uMmzdvSqj197YAZyq526RJk/yYylFjh3AUcuFKSlHADJXkwEERIzhKNXFVBByjvKzMEa6lHdbzRDV6oLpDuoUzAeJJ02qNC2nJdSmpaOmsGtTYafWNdCR9KylFQd40kXuflBI3AVoaly9fljCpdKL7dJ6iJCiZUX0kQVmvBV4Mre5RREfgSfepfYh0Rkr1m4RLiTSdQ9TMlZyDL+zevXutSjtXr171j8gH1egBR7gaAoU0jHKQV6IJrSahi1pQY8cXcoCSH10M4oxnWA+QR00475NS4ko6tU7LgXDiirhBMBj//vuvvxUNudHcuXO906dPy7aW0qoFIWHsADGm+TKuX78uoVYVo+Clo6MfRFVfcIzitA9XU/WlrIePMAvfSg9BSE8aMiCqe0oWTfC8T506Jc7mtsi4MKLv378XvxTGKqmFMIsewHVN5L66hyOxWkgchJM0ob+ybNkyyVGDTssgCPrXX3/1Dh06JIlHjoc4iUdIhAqlyqgm4zD6IpKL499Kq25QjMfgapVC7wMR8f/JEcnVg0V6ttUxSxM0v3HWrFmyHUSPCf4OF6lFD1pyJY1ZSE99Vn369JEwSJom0Je21mqLmbb8hruXZNUE98M1OB+/ZxJhPUAuNdFSwnGalgdKEexTS9HSj2kN+5L2J7F//34598yZM35MPM3NzZ8aGho+teQofswXWoQg9xm8zvHjx+XanNNSTPZjP0M856TR8sLJsVH/Mwy/P+o5cB/cG8uaNWvkd3CMxm3dulWO02fB0vKyyv9W9Nq6cGyl8Huz/OY0uGfuIS699R7j9idBOpFenN/Y2CjPgGfG/4wiThPEcw7PMZj2HMe1eQ4cE0Tj01BdESahaRb1HFzRRFacN1L6EOJEp/urASFyblgwcWjCZDFqSXCNLIYHgSOOtPtjPy8Lgis6mt5tqQd9zlHwXNFJHPXWBMYg7bii6SE3RiqOtP1JkGtUmrtrLlRtzoGoOT+YK0WB0Li3tOO4XlRu3p5ommRdKiHtnGquGff8tCQRZxCVemkCY5qmVxf1UCvVvd11JEl0vMjViBIo0mYRYBSICRFUIwRy5WAVIAhiJ/fj+ogx7jiFl4LrVfMb8sq30AMvNYsaCa6jBiprGn8rTXA9SmmkMZrg3uIoqh5yYaTIZaIgMdhfSWlIhYwoay2itzUIkntDaGm5allpaz0ABoJnznU5n4XqX5rfpx6gU+5LfUdlxGkjlSa6akVp5BPTQzkpRI/zWnrxGsXD9FAscmGkgn04grx69UrCeswdZLiD6aFcOG2kVHRx47D0c9tRXfmN4mF6KCdOGykVXdo4rO7du/trRpExPZQTp42UTgGhY4TC6EDLaqdDMfKF6aGcOG2kmKZk8ODB/tbXMNByQobBwUYxMD2UE6eNFIM9k2bMZKDltGnT/C2j6JgeyomzRkpnKJgxY4Yf0xqdF0en6zWKjemhvDhrpMgVKbrH+ReYNnXBggXWJ6YkmB5KjN+p0wkYisD4I7r/MxwgPJ6J4QHsJz441sooJqYHA5wyUggNu0nIEIcwwf1hwRrFw/RgQAf+tCS0YRiGkzjdumcYhmFGyjAMp3HaSAW/x69L+KMGRnno3LlzKy2wvXbtWn+vUVScNlL6NYrjx4/j4JcvgfDlip07d0q8US70U2HoAD2wzRdT+LKzUVycNlJ04APtoEcfmF69ev33LTqjXDQ1NcmwGO0LpWP49COYRjFx2kjxcU1EyffmqOLxPTCGRsybN88/wigTfG1ah8XwrTu+PYc+rJd5sXHaSCFKqnf4H7p27SolK7ZtlHs54WvTVO/QQ0NDg+jg/PnzqR9NNfKN00YKUao/qrGxUXJPG/ZQTnTsHv6o5uZmMVJM3WIGqvg4a6RUlHz7Hn777TcZvxX3SWuj2FD1xzCRSWGYyLQOHjzo7zWKjLNGCoMEWnIaOnSohIcPH5bQKBenTp2SRhNlxIgRUqqylr0SwLAY19BPE7EEP0/EgFPiGFRqlAf9kCsL66DfT2SxcXvFxsbuGYbhNE47zg3DMMxIGYbhNGakDMNwGjNShmE4jRkpwzCcxoyUYRhOY0bKMAyH8bz/A3pqMPRMvn45AAAAAElFTkSuQmCC[/img][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAg0AAABDCAYAAAAf1TahAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAABKxSURBVHhe7Z3ri1VVH8e3z0MvrWb0RZSENQZFRVFeQjMosLHsRSF5KYggSZMIrOgyVjxQWSOYIOEthQi8USJIo2aQkCWmJgZJQSkh0avRyv4An/ms2b9pz3bty9lnzsw5Z30/sGftvfZl1t7ru37rt9baZ+1xlwaIhBBCCCEK+E8cisBYvXp11NnZGY0bNy5avnx5HPsvK1euzN0v2hdpQ/iQLgTIaQgQCvfJkyejCxcuRD09PdHZs2fjPYNQ4P/888/M/aJ9kTaED+lCGBqeCIwffvghuvPOO6MzZ85EN954Yxz7L9988000e/bsqL+/P5owYUIcK0JA2hA+pAuRRE5DYNAioBVw4MCBOGY4ixYtcuHOnTtdKMJB2hA+pAuRRMMTgUHBvvvuu+Oty9m1a1d01113xVsiJKQN4UO6EEnkNAQE3YyMO15//fVxzHDoZoTbbrvNhSIcpA3hQ7oQaeQ0BMRPP/3kwltvvdWFaY4cOeLCK6+80oUiHKQN4UO6EGnkNATEuXPn4jU/v/32mwvHjx/vQhEO0obwIV2INHIaAuKrr75y4bXXXuvCNPYzqTvuuMOFIhykDeFDuhBp5DQEiO9nU/Drr7/GayJUpA3hQ7oQhn5yGRDM1AZZWV60X7Qv0obwIV2INOppEI7z58+7sKury4VCGNKG8CFdhImchkCwscesAm5vSU+ZMsWFowFpYuIYmxxmrNi0aZNLg/18LDSaURvQDPoIWRuyGX5Ctxej4jTwcOnGYuGjJ60Kabf7aDXB/PHHHy4cjQK+b9++aNq0abl5zoQxDz74oHuBaqxnklu6dGn0/PPPRytWrHAGqRaSmmB+/lZkNLUBPDP+lz03X1lqFn3Uow2we2SxlnmrIJvhp15NtLrNqOQ0JG/alrlz58Z7RSty8eLFeK0+KMzz5s2L1q5d6+aip5WSnviFSmLx4sXRxx9/7ApgM3Dvvfe6aXIPHjxYU0F+5ZVXoo0bN7r1WbNmuTAPM4ytxEhpAzCymzdvds/51KlTLu6WW25xodFs+qiqDbAyMHXq1MLvMlBxog1fhdmMhGwz6tFEy9uMSxV57rnnePPFLQOZfGkgs+M9YdLb2+ueRXd3dxzTXPT19eWmbyTSjwY6OjqcNrLgGPSSd8xYcvjwYfccCMsyYADcOUVlwI5jaSZGQxtgz3bHjh1xzOU0sz6qaAMoEz09PfGWH7tvrs/zrkLV9GUhm1FM1Wfeyjaj8vDE5MmT47XB7quQv27GOButp2bmxx9/jNfyyfppVRm+/PJLN+XsfffdF8dcDsfwtbyXX345jmkuaEHQKnznnXfimGKYAGfAqOWWAbqmX3/99WjhwoVu28aLm4HR0AZs377dhdOnT3ehj2bWRxVtkO+Uidtvvz2O8bN161Z3bbAJk8Ya2YxiqmgCWtlmNPydhvRQRrLrLRnPArxk0tnZ6bYZ8vCNAzIfOi+i2Hk4LXQRpY+lu4/u0ORYGcemu/9sny3AMZYO1klL8hgbhyUk8xE1fPHFF0PHpM+xBTgvGZdO01iRdAZrgWe/Zs0at55XKXAMhazeCqiRPP744y4ffdrz8f3337ux1jzefPPNaKClNPRhHxsvbiWqagMos3RDU1by8r7Z9VGrNuxlwbwyQWXw/vvvR6tWrRrabiVCtxm1agJa2WY03Glg/KanpyfeGg4VbUdHR7w1ON65bNky53kCGcGDS4IjwLfd+bLa4cOH3RgY16DAPfnkk/FRg5U+42QYqi1btrjjuru73f989dVXhyp98KWDYywdsG3bNnd+GjzNS4nfKHMM2yyMedm4rWHbnGfPhQLxzDPPuPVG88ADD8RrIweO3sSJE6MTJ064bSoGHCHi03AMTlwWVC72klzSkSIfceLKvjWNTuw6nJvEHLWs93Bmzpzpwu+++86FSZIvbJEe0ohO82bEQ2uk4cUXX4xjmpNGaAPIM8os5YmyZs+fvE5TpA/TAQt5YdBo4Jo+zfkg3+w6yXQknXmfI5+nDSoNbAfX5Hz09eGHHzrbklfhcc5rr73WtJWibEa+zcjTBLSbzRiVX0889NBD8dpwKCRpD5PKHWfAOH78eLw2yAsvvOBCumyoeOneWbJkiYsjI9KGCE+NzOG4p59+Oo7990MrkE4HnjOVPucanF+l8PC/rXspzVVXXeVCXgCybirrnUg6NaOBTRdbBV5M4nlhHLlXc5rSLyzZPeW1TN577z1X+LgOrS+g0H399dfRhQsXLivMPmipffLJJ262OozRG2+8Ee8ZpK+vz4VF+ZnunsWg4YjSskCnv/zyS/Tpp5+6fffcc48LffCWNfdFHmd9LTALM1Zll0ZQjzaAPDNnmRfATB9po1mkD/IVHfDcMb7kMeAw0P3v05wP0kPZozLCkUlWVEln3ioDH2lt4DDMmDHD2au9e/e6tGBvaNzktSjRNjq1RgN6bRVkM4bjG84ZC5vRaEbFaSjL+vXr3UOi4BrmiQICsmGA5Pfbk19gw3EAejgQ4bvvvuu2YdKkSfFaPpwLpIdr2HZVHn300Xgtio4ePRqvDRY6eiaS99so6jX8ReCsYYDvv//+OKYaFHA0wDMzg75u3bro7bffjo8oBifQDAWGBM0ku3z5Ih/GqpbeHbRHLxgVCnogjSxWIWS1GqxCMmNoGjx9+rQLizBjWnapQqO1Aab7PENZBPlqNoLnToVMPqOTsq1J4Fjyg+vRy8cb8ElwKGotl/RyUkGRJjtvzpw5LkzaqiQ4GjSC0Df3BLR0jx075tbHGtmM1rQZjaapnIYikr0DDB9Y62r27Nlx7HAolAgBI0FhzDqu0ZjxAIZKAEHi4FjPicGQBsZ/NByJkcQqhaxP6NaK9fzwIpBVFFWwF9B+/vlnF8L+/ftdd3At16SbGdLdhYxNUsH4QH+kn56kNH///Xe8FgaHDh1yYZahrBV7cY7xbvRRFbqNqSDIK4OWYLqlmQeVH2WZnkkqH8PeZ8jqseDlR+zSww8/HMcMQsVXBF3cyR6mpB0kTO/zDbWMNbIZl9MKNqOlnIYkvb29l7WyWKxXgIJ80003ud/2wu7du4cNe4wmCM2GOug5wWHAYNANljYYY40NmdSKVQoj5exgfPHs8cqThrhWzJBY1yGFktZgre+QcA4tkKTR4FpUFlldlryPQwWQNOJj5biOBFW1AbTmswxlFWxuBxuarIo5H1bB0zokj2vRsfVuLliwwIUGFQ34roUNoOHDucnK3a5VBHYubfvMvhGm99XbW5qHbIafdrUZDXEaGE/iZkea5IQfRT9Lmj9/vnv4VMz0NoxUC6eIrK++PfLII/FaFH322WfRhg0bav6ZzmhQ1esvUymYcSjzkzLrokt3HdeKGZKTJ0+6bZw1nntei8EmrTG92bhqupuZn4JBeiIa4BzymLH8pPGu1XE1w1F2aSRVtWHd0FmG0qhFH4z3kq9W8VTFnA/r+kUbeT0XaW2AdeOnbQyVBsMfPnj5kQolqQ2WkXSsRovQbYZPE2NpMxpNQ5yGzz//PF4bWXjRyODh2hgU2BuqNg5l7z7Q/Wf8/vvv8Vrj4P9iJFkwDAY9CggRaGFALeOwI0VWV2k9n7gtWykARjT9cmsarrdnzx5XMXBdtuuBlsNff/3ltIEhKHru3377rQtvvvlmF/ogTcxOB0ldGrzIZC/hJjEjWHa8OGk8yiz10AhtgHVD571YaJTRB5UDxpgWZb0VhOUPXb/YEDSc10otow2wWQJt/DoJ/4fWpv3EMomVIat0mgHZjHybUVYTo2UzGs6AoanEwM0NzVQ14C3GsYMzZA1Uji7e6OnpGXZsfzwL1kAFO3Qsy4CH5eIJLS4ZDzYLmW8hTcaA0Fwc1+f/sAx49kPHsp6VDu4hDceSdjuGe0qSvLYt6Znvks8sa9Y3+x++NNRD0XUtXVX+r81axgxyRfBMOJZn7oO8No2YDnhWrCfzF9jHsUUkZ67L+r9Jurq6Lrsu+rB08YxIi12XOJ6B5bfF+56l3T/6bBa4r6z0Avvy9hdhZcPKWx5F+mC/6cB0R7qIZ9vIy4M03L8vz334jkvqn3vkf9tsitgJsz3AftNSGvaZ3SpTltJwr2XvuQyN1EU72Yws7bSrzajkNNgNFi3AQ0jHcz7wQNP7IB1n8QYP0QoXC+v28A0TEvvJPP4nGWXnsBSlI4nvnpMZzLWT/y+dHjBBs5/jfdg1qhTEPPifeddlX9X/W0ulwDEUsnRhJp40kpc8J4PjuDbPJX19iy/CCp0vT9KYXtPPgXNJHwsVAWnhGIszLZkxZOFekgbHrm1LspIbS0g/6cnKe0tv1v4iuH5Zg5elD3t2SWef0OxA2om38lomzfwv0pjUnQ9LQ/qapMPKLemx/VYu2Me10YKllyWd/3YNu05RZZUmK31VaaQu2sVm5D3zdrUZlZwGUR1EkRb/aGCiyyrgtr8KVnDLYgWhSmsqCdco8ywpaGWOM+OUroDaHcv7RmjDHOVanulI6MOchjIVLxVYUeXQCtqw55aVj7XCtfKuZ/ur0A42I1h7EYeiQeDVmpeJCCkstbYgRoKiAl60PwurFMxrLot54VU9Z4xImWdJ+sq0LLierzUTAo3SBlgrqtaKrF59WLkrgv9TdFyo2miULtrBZgRtL+JQNAjEZ4WLparg68X+vw8cmrz9WXAerTQKIuu1QuGl0FUpePxfCrcPrkeLhILN8y9KG3nC9Wqt2NqFRmgDyF8MaxmnzUdVfZCPeeeQJu6LfC+6dsjaaIQuOK/VbUbw9iIORYPAO6Zg1eMhjwSWBh+In/21GHcKmJ2TVRDHCioF7tV6eEQ+I60N4NlzHsa4mfKASod0oZGxLI+twEjrQjajPZDTEABFBbxqxSBaH2lD+JAuRBYtOyOkGHnqmUVNtDfShvAhXYSHnIaAyJpIxSa9qvpdfNH6SBvCh3Qh0shpCAAr4FlzxJ87d86FvqlNRXsjbQgf0oXIQk5DAFgBL5oj/rrrrovXRChIG8KHdCGykNMQAPZJVZvDPI19mGW0PuolmgdpQ/iQLkQWchoCgO+3T8342h7wYZbuFvy6nqgfaUP4kC5EFnIaAuDYsWPer+0ZfHHvsccei7dESEgbwod0IbKQ09Dm2CdoFyxYEMcMxz7BO2fOHBeKcJA2hA/pQuQhp6HNoUVAN2LW2OP+/fvdN9z1e+vwkDaED+lC5PHf/w0Qr4s2Ydq0acz0Gd1www2ucH/00UfRNddcE++Nos7Ozujqq6+Orrjiiuitt96KNmzYEHV0dMR7RTsjbQgf0oUoDdNCivaCedTJWkKme02T3N9sc8CLxiJtCB/ShSjLOP4MiEEIIYQQIhe90yCEEEKIUshpEEIIIUQp5DQEAC8xjRs3bmhhe+XKlfFeERL8nC6pBZYpU6ZEO3fujI/4F+LYJ9qfRYsWXaYL4s6fPx8fEUWbNm1yL0yyDxvCtggPOQ0BsHfvXheeOXPGvSHN9qpVq6J9+/a5eBEO/Iyut7c36urqclpgefbZZ6PFixcPVRD8Dn/u3LnRmjVrnGZE+2NO444dO5wmyPcTJ05EH3zwgYtHE1u2bIl27drl9uNQLFu2LDp79qzbL8JBTkMAnD592k0Ja7+rtvnkL1686EIRFnw3YOHChfFWFM2cOdOF9r2B8ePHR9u2bYvWrl3rtkX7Qw8U2IRN2Ap6mZjkCbAZx48fH7IhTzzxhAv/+ecfF4pwkNMQAIcOHRqaEpaWwfLly50ToRndwuTgwYPRrFmz3DqVxYoVK4ZN1kNvxIQJE9y6CIOjR486m0C+0+PE0ANTSS9dujQ+YjhHjhxxx2dNACXaFzkNAUAlwXAEY5F0S1PQDxw4oIohQGyK4Hnz5jk9zJ8/P3rppZei9evXx0eIEKFhwXAEmpg4caLTCds+p4B9mzdvdsMVIjzkNLQ5VkkwRtnf3++cBrqh5TCECS1Ke5/h1KlTTheTJk2K94pQoWFh7zMwdEWPpG+aaOwJjubu3bvVyxAochraHKskMAA4ChgEWgkiTJJDVRh9upi3b9/utkWYWMNi+vTpbvupp55y359Iv+Qoh0GAnIY2Z8+ePcN+NsdYNq1L/XIiPBirpkU5efLkOCZyDgRvzvvegufDREBlIdoXHASwnoUZM2a4cOvWrS4EtLNkyZJo3bp1Qw7D6tWrh754KQLikmhbent73XzxLKxDf3//UJzmkA+L7u7uoby37wv09fW57Y6ODrcNSd0kF9F+oAPLX/RhTJ061cVt3LjRbRPaccnF950K0d7o2xNCCCGEKIWGJ4QQQghRCjkNQgghhCiFnAYhhBBClEJOgxBCCCFKIadBCCGEEKWQ0yCEEEKIUshpEEIIIUQp5DQIIYQQohRyGoQQQghRCjkNQgghhChBFP0fE/lTlw7lDaEAAAAASUVORK5CYII=[/img][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAp8AAABmCAYAAACN6vrwAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAABkKSURBVHhe7d3b6xXV/8fx8XevflOvSkLSi8Ik8ZCQKRikoiEJllY3gqFpESSpqXURaaVYQXiMAokozaCQPEOClpiHUCwKSomorjxVf4C//VzN+9NynNkze39m1j69HjCfmc/M3rNm1rxnzZo1s2cG3KiJREREREQC+L+4LyIiIiJSOVU+RURERCQYVT5FREREJBhVPkVEREQkGFU+RURERCQYVT5FREREJBhVPkVEREQkGFU+RURERCQYVT5FREREJBhVPkVEREQkGFU+RURERCQYVT5FREREJBhVPkVEREQkGFU+RURERCQYVT5FREREJBhVPkVEREQkGFU+RURERCQYVT5FREREJBhVPkVEREQkGFU+RURERCQYVT5FRDrUgAEDXLd///54TFitTl/az8aNG11MTJw4MR5TPsVd51PlU0SkQx0/ftz1Z82a5fqhWfqTJk1yfZGVK1dGM2bMiKZPnx6PKV+r4176T5VPEZEO9fvvv7sD/a5du6IhQ4a47uuvv46nlu/KlSvRsmXL+lqeFi5cGE2YMCEaOnRo/AnpRbRAjho1ysUE/UOHDkWTJ0+Op5YvdNxL+VT5FBHpUMeOHXMVwr/++iu6evVqdP/990ebN2+Op5Zv5syZ0enTp6OLFy9Gly9fdv0qW7ik/VHxnD17drRixYroxo0b0fz58934KlvDQ8e9lE+VTxGRDnX48OHosccei5YsWeL+Hz9+fHT9+nU3XDZamahsHjx4MLrrrrv6WjurbOGS9vf8889HGzZs6IvBwYMHV94aHjLupRqqfIq0GDfoc9mIS1Zc0kxau3Zt3enSverFxqVLl1xlcNGiRfGYKDp79qyrGDarXno7d+6MFixY0FepIH3ofs/ulxUXXOomBufNmxePiaJff/21363hoeNewlPlU6SFqFh+99137tLRmjVr+g7ohoL32rVrmdOle+XFxqlTp25qYWI699o9+eST7v9G5aWHESNGxENRtGnTpmjkyJG637PLFYkLq/gxbdu2bdGYMWPc/80IHffSIjdEpCXOnTt3g12wdhYfj7nZ8ePH3fTLly/HY6RX5MUGli5deqNW+XPxwedqB+Qb8+fPj6c2pkh6M2bM6Jv/hg0b3P90fHf79u1uvHSXomUUn6OrVRbd/4xnuNGyq0gclhn30jpq+RRpkR07drhfbGZdLuIGem7eV8tS78mLDfDDH35ZPGzYMNcSxKXOLVu2xFMbUyQ97u3jXjvSvPfee93/tDitWrXqpsuu0j3y4uLBBx9008eOHes+u3z5cheLc+bMca2fjZZdoeNeWmcANdB4WEQC4p6m2ll8tH79+njMzbjfiRv5eW6e9Ja82Chb6PSkMygOpSpq+RRpgfPnz7t7Oe+88854zM3smXW0MElvyYuNsoVOTzqD4lCqpMqnSAv8+OOPrj969GjXTzpx4oTrDxo0yPWld+TFRtlCpyedQXEoVVLlU6QFfvvtt3goHY8rwcCBA11fekdebJQtdHrSGRSHUiVVPkVa4KuvvnL922+/3fWT7PEi9913n+tL78iLjbKFTk86g+JQqqTKp0gLZf2q85dffomHpFfV+8VvFUKnJ51BcShV0K/dRVqAX7Ija/fLmy7dK/S2V6xJGsWhVEktnyJt5sqVK67P22NERES6TVtXPrnvzR45I9It7H7OrMql/eqTBymHxHLxOk/e390qPGSa9Ht1v8+LjbKFTi+PYrA9KA4Vh1Vry8onze90BOKUKVPise1t165d0cyZM/uW3S4hpNm4cWPfZ1S5zufnazf4888/XT9E5ZJWVApRHt5cLw+JX94Uwg+cGG6VJUuWRM8991z0wgsvuOVuBPuSrePEiRPjsZ0lZGwgVHr79+9328S2D2VgUjfEIPzyivXuRN0YhyoL20vhyicbjgLDL0DYiFXUzC9evBgPdQby5YknnohOnToVXb582b2VRqRZf//9dzzUP+yzHAivXr0a/fzzz9H27dvd6+iS2H+J3507d7oCr9V4Zd/BgwfdqxzXrl0bj83H986dO+eGOXjkYd6UYzoBrBYH8NmzZ0fvvPOOKx9pVEi+PKFbYhB8j9fiYtKkSa6fhRY2jqPsp1IdlYX1taQsvFEAL/uvFRjcBexe6s8L/ekYZhzdJ598En+6HDZfunZ32223ueWcMWNGPCacWkW3ZWmXybb18ePH4zHda9++fXW3WVnb1OZTO5mLx9yK/Zh9m3253RALjcYEZRXfIY/rsc81Ov+q5cVG2apOj/iifKwXX90Wg6hVPm/UKjfxf9n4XMjtXVS3xaHKwmytKgsLtXw+/fTTrjWSM9atW7dGQ4cOdR3DdvbA2YLdt9FL7JVgrUB+v/fee/F/nSvtElw3+/777+Oh+vr7yBFig3223nyOHDni9u0XX3wxHtM+OHunfFm3bl08Jt8ff/zh+nfffbfrZ1m1alVf69Tvv//u+u2gaGyUper0iC/Kx6lTp8ZjbtVtMQjWJ+9yJ61MZ86ccfNvt0erdVscqizM1qqyMLfyyT0r7CCwBfRRMTWbNm2Kh/67b9M6UMkYEt9v4Vc42Am5fG+fzbvvI3nvBn2+71d+/ftu6EiDdWHe/J93mYNLRf4tBnyPpmnSNsxz7Nix8X9RdOjQodx5py0X6Pvj+RxpWXM4nd/szufZmdhZYGnbd33kta23Tbd0fcl1TnbMJ2350/KVbcEN0/xv24mO7USF3TCd4Dfc4+vP24atSyKd5H08pJG81yptuelsuen7y9UORowYEQ81jm1JbORdcnnrrbdcodauz9Z77LHHXGz7+109HMTyDjLkDfPjfirozSrVII+JL9x///2un6bbYhAcM+tVuLFw4cLo3XffdQ05Vo5L+VQWtmlZGLeAZsq7tG7NwXS1DRePveGat+1yNJ0/HzqawcE8bZw1+frj6Hz+fG0eNm/G03QO+jTh2zyS6ddr3l+zZo37TG3DufSYF+vGOPqWhikyT5NcLr+Z2y490JGOpel3yW1g47PStnlweYe00/IbdlmCjmZ4Psv68z99/re8KJKv/nT465ZcVj/tZLN/Mo58abHgr5+fV3nLTcd6hmDra8uclDc9j59f1jEuDdNsGyX5eeZvM+KDvMqaZxLzsfxO7j+2rnTJbQ/GMS3t0hHLYZct6UiD+TMuC2mz3MzX5t1sPlehv9u+UVWlt3379r7t4neMT2J8VgyC/ZhtRufHgZXTafNMw3etTGukHK0XgyDv/LLSlov4zMJ3LC3bx9pJVXGRpar0iBnm63dZ5RbTVBaGKwtzWz791sThw4fHQ+mshRTUtv2zXVpxaulFtUyJx/zLfsXFeJqWQctVFlpXuYxTy7Ro5cqVbpzdGMz4zz77zA1zNvnQQw+5YXCjcS2zo1qhE49JR+vX66+/7oZp4mY9mNerr77qxrGOlkYzksvlmzVrVjz0bzq0KpNntYCIx0bRhQsX4qF8nNXYNlm9erVLm7wl77B582bXx5tvvun6tYB1v/Ljs4sXL3bjapU89/gfy4tG8vW1115zfdattpO6Yc7eikrGka9WyLttznwtFlg/1gH+LwSTy3369Gm3Xiy75Qf/+2eVtPTSKuq30odgr5lrFtuEG+pRK5RcDDEuyVq/s1pY3377bRd7zIttxr5BeUBL9bfffps6zzSvvPKK20eJEeKRy1uG7cb2Yhvcc8898dhbJS/LsezTpk1zw2w31hHM38anYZ1oAaGsafQ1fsnW87zO8rcXsb3ZJmzX2gHQDdMlf8SRF4PE27Fjx9yPRLi68eGHH7rxXAUaM2ZM6jzTMB++y+VtyouXX345nvKv2gHd9bPKZqRdGqa8oezkWMGy8MMQjh+sd9arcVkWvmPler2WqSTyKy3Wsjq7EtWrVBZWUxaWIdijlqxywH2iZA7/k2l2v2TRS4zbtm1zfb9C4u/kn3/+eTx0M5qVrfJF+vyCLI1fMfIr237FMCuNMtXOrvoK1QceeMD1cfbs2XgoH7/YM34eWd7t3r3b9WHbgTxqRFa+Mkznz49L22Wy5U/Ol8sTYJ2sUEnil7dWmfZjyZ6xWaX+Vi6LOHr0aN0DYBHr169333/44Yfd/59++qmr0FMINxIn7PP+fKhM+JjXSy+9VHienCDMmTPHVSI4wbKD9yOPPOL6o0ePdv0kDhiUH3Zyad/77rvvXD8PsW1xXaSzk+lGhIgNX5Xpkd/sg/UOgHnYRvY7Aw6U7PNsc+ZLmVMU8+F7oDLMQZrKgxk0aJDbXxYtWhSPycdJKcvz0Ucf9S0L6VCByDphBifNNLbYvmnHPvIrDzGVFmtZXdZxLk83xaHKwlv1tywsQ7DKZ5oTJ07EQ8X4FQkqif4ZXllC73RV8ivSfl754w07J7LuJ2nmzIgAp4XCWozS0m1WVqWyTJwgUYDbiVMnoQWm3gGwERRMFG4UVM8//3zThTgFKvOh1dkQbzyirJGDPlceqHzY1QhjLQJZlT5aKSjYraA1169fj4ekTCdPnnT9rANgo+weSu7N4yDeLFpM8dNPP7k+Dhw40NBBH7ReUtH0GyZAi1NWCyrlFvvm8uXL4zH/+eeff+IhKZPKwlu1Q1mYW/n83//+Fw9F0Q8//BAPpaO1LhTSSp7l0TV7ptft0vKKzhCIoOCk0siOYL+kp6UgGaR5OCvkx1icXXFjPZe3Q8ZHNxg8eHA81Bhrcap3CbFRdjkoeaBtFK1XxJj54IMPGj7oc+UhbVn27NmTGWO0CnDyQ6Hrn4hJdWhxQjMtwGnsUqT/I9dmWEXEDtCUdbRgNnLQt6t2yWWxHzr6V6t8lIV8b9iwYX0xSExKNVQW3qpdysLcyqd/ySTtl1D+T/Pnzp0bDxXjP2j4119/jYey+fdBVPVoiiJB6lfI20VafrCTGP8SUxpa9zgTo6PSSOEILits2bLFDRdFcNvtEbRQcEmq6A5V9FEPRQ9oAwcOjIc6T7MtRtbilHUANJaHefseBTitBxTiDPeHtRTYCQ6FZL2WZXvgvl9WUHAmWzKIbwry8ePHx2P+QzqcDHG/VtbJVxG657MxxEzeCWfRGMQbb7zhDrRWqW0WJ9LMxy4xctDnns2sMiotBu2qXXIf/fLLL10/7Z49u3ecE3E/Bu3ezyKIqbRYy+p6/Z5PlYU3K6ssLENu5XPevHluRwUVChbeZ/cV8hk+2wj/+VNUWGxj8oieNBQOVqHinh3/0Ud8lx0t+YidRvlB6rf0+oH26KOPxkPtg/xgGekILnBmZRhnFVD65J3/6Cbyjnnw6A8LRiq07AyNnInBP0nx75stcsLwxRdfuD7L6+d5GjuwcanCZwcVKtLNXhYJIatA7O+JVSMtTuxP/qWfJPYvWnf27t3r/rfCvFl2sOYSIze8c+9tPd98843r13tWHctoj3mbPHmy6/tIhx+rpP0whRgqejtIiHs+Td7Bsmxlp8e+W7TFKS8GwTFh3Lhxrkzj4N9fHLC5xEhZSHlR7/7RIjEIjmGsB+uTLDNJx36YlJxmeV/kNjRiKi3Wsrr+Xgns9DhUWXizssrCUtQCNBc/7a9VLqkau5/w187c3Pha7dmNY1rysRK1ikzfd+jSHh2A2gr3fca6WhDcNN7Sgz0SIK3je/ZZ+v48ameXbnwRrCPfYflZD+ZljzEgDR95Y2nY5+tJLheP5TD+vGoVp751sXxOjoctl9/ZY0T4nL8N/C65zdI+Yx3rbJ9NLn9avvrrYevH55iPjffjgXnbeOtsWybjiHkbvmfTLB0/PvzPJpebPLXx5GlyPFhmxjUSO0XYcmTtE7YsWdPzkCfJOM1CrJBWWtxantm2Z778z3jijr6xdSqCz7F8fuxnYdswbx9psywsMx37q60H25x8S8ZD2jbku0yj89ellfJio2xVpWdllr8PZqkXg2A62xg2X5aX8f7+Wm9bJ9m+zfpnpWvSYtDKLIszloV58jkru1hmm7flcxo73hTZH0KpKi6yVJWeysL2LQuL5VCNrZh/oGbY38F8tgH8Lo3tpEwnE8ko29D2PdLxkYl+pYvpZKifaVa4+F0jgc33CQr7LsNpG82fv3X11Fuu5HjywAImOd74eUX+EXg+225Ms8+kbTPbBlkd30PRfOVzlqatR/K7Ppbb/7xtS1u3rO9RGNgOyDT6/G+FhMla7rT52/rYd+iXyZY1Ld+QXI5GJA+Kechn24995AvL6VcerFDj88n8tXwsgu/bAboe1j8tH0ibeTCNbU0s23owjnXhf77nx0VyPoy3jvm0g7zYKFtV6Vn5nLeNkRWDLJNtG5sPfSuXkzFuny+yv1osJ8vLJJtnWv6QPtNYdqsEW+WYcbbvWF7QJePML5fSYrRVuiEOVRa2d1lYLIekqxHABCRdcifwC8cyC4ZelpefNr0ZjbQ4GZaj0e8kUeBS4OUhvihskwV2khWgRQ8c3cK2fah9rar0KEvYzkWVEYM2j7wKJdhPkpWMpF6NQVQVF1mqSE9lYXtT5VP6KpjsNEm2M9KxE0j/WX5myZteD2etaScReThg8z1rwWkEafHdIgU2B/y8zxFzFLZ5lYNu1J9t34wq0uNgyjwbvWLQnxgE6RWp8LJ8aWWdr5djEN0QhyoL21u46JK2ZWeIyZ2GQprCnGm9ePZflXoFLYVXven12IlCowd9Y7doNFrQkV5WaxPzJIZYL+ab1ypFLHLQYF16UbPbvlllp8d2bvagj2ZjkLSoUGalyfwo24irep9Dr8cgOj0OVRa2v3DRJW2NQKdQtkKAjgMIwV/kLE6Ks7xNY4VmXstMEoUa82y2sK0KBSzrw/L18sG8qHqxUYUy06OcsNjNu5QYGq1HrCcn0c1UintNJ8ehysLOMIA/tQwRkQB4Tt+UKVPcYy3SHoOSN126V+htr1iTNIpDCaGlr9cUkXSNvlFKRESkU6jyKdICWQ/ftjc8jRgxwvWl9xR5MHuZQqcnnUFxKFVS5VMkIKtcZr233d4O5b9CTXpDXmyULXR60hkUhxKCKp8iAVnlMu+97XfccUc8JL2iaGyUJXR60hkUhxKCKp8iAf3111+un/WuYXsvfTu/k16qkRcbZQudnnQGxaGEoMqnSEBnz56NJkyYEP93q+vXr7tffUrvyYuNsoVOTzqD4lBCUOVTJKBTp05F06dPj/+71aFDh6K5c+fG/0kvyYuNsoVOTzqD4lBCUOVTJJDz589H165dix5//PF4zM143h0efvhh15feYbGxaNGieMx/9u/fH40aNSoaMGCA68+cObMvVppVL71Lly5Fy5Ytc+nRLViwIJ4i3S4rLq5cuRJt3LgxGjJkiIsJ+mWoF4dMI9YtPeKQZZDuoMqnSCC0anJJPet+zgMHDkRLly7VMz57kMVGcttT8Zw9e3a0YsUK3kYXLV682H32nnvuiT/RnKz0qHjaJdDLly9Hn3zySTRy5Ej3v3S/rLigErhnz57ozJkz0cWLF0uLiXpxOG3aNDeeONy7d2+0e/duPQWkm/CGIxGpRu1A7l5dyiv9eMVf8rWDvAaO6YxnOu//ld7A9q4XG2C8/5pAPk9MNaNIerxzulYZiP+TXpAXF7wWknKK6WVoJg75DNWVspZBWk+VT5EKUbhSaNJPe5+vPz2tEJbulbft7T3//gkJB2XeT96MIrHGdCob0jvy4oJKIHFXlmbikOFmT7qkPend7iIibcjeeW1FNJciawfsaN++fdGsWbPcuLJxf12t0tv32Bvu9Rs6dKgblt7EJXfePrRy5Ur3f4iYSMYh9zrPnz8/Wr9+vftfOp/u+RQRaWP88ILugw8+cP8PGjQoWrt2rasEVOGHH35wfSq/kyZNqiwd6Rz2/GFOgMr4wVsRxCGxx4/fbrvtNvcGpF27dgVJW6qnyqeISBui1YcfY4wdOzbasWNHtHz5cvdjoDlz5kRjxoyppPWJHxitXr3atTx9/PHH0bfffquWzx63YcMG90MjYoKK4Pvvv1/5A+FJ85lnnomeeuqpaMmSJe5RTKtWrYouXLigh9F3CV12FwmISgSFqo8KBQW63mokIiK9QJVPkcC4bMUjRLZu3eouKz377LPu8SWnT5+OPyEiItK9dNldJDDe6PHII4+4YS5pjhs3zj1oWUREpBeo8ikSkL3Rgx9ygIeIv/nmm9G6devc/yIiIt1OlU+RgE6ePOn6w4YNczfwv/vuu+7tHXqFoYiI9ApVPkUCOnr0qHuFJrdab9++3V2C7++rEkVERDqJKp8iAR0+fDiaOnWqG543b567BH/kyBH3v4iISC9Q5VMkEB6OTGVz+PDh7n9+bMRjlnbu3KkHeYuISM9Q5VMkEF6V6PfBw5MPHTrkHrckIiLSC/ScTxEREREJRi2fIiIiIhKMKp8iIiIiEowqnyIiIiISjCqfIiIiIhKMKp8iIiIiEowqnyIiIiISjCqfIiIiIhKMKp8iIiIiEowqnyIiIiISjCqfIiIiIhKMKp8iIiIiEowqnyIiIiISjCqfIiIiIhKMKp8iIiIiEowqnyIiIiISjCqfIiIiIhKMKp8iIiIiEowqnyIiIiISjCqfIiIiIhKMKp8iIiIiEkgU/T/x5yDerkJ3OQAAAABJRU5ErkJggg==[/img][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWoAAABECAYAAACoCX8RAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAA5tSURBVHhe7Z3byxXVH8bn/d13Uq8qIrKLoKAoU+gEBZVUFwWVdtNNgRkRlJVmRUQl2RGiMwldpUVRREeDvLBCysSo6MZXIqIrO/8B/fbn6zy63mlOe+/Z+x31+cBizV6z9sw6Puswa9bM/DsgM8YY01v+l9vGGGN6ioXaGGN6joXaGGN6joXaGGN6joXaGGN6joXaGGN6joXaGGN6joXamCF4/PHHswULFmQzMzPZrbfemrse5L777qs9b8woWKiNaQkivGvXruz333/P1q9fn+3duzc/sx+E+Y8//qg8b8yo+M1EY1rw7bffZmeddVY2OzubnXLKKbnrQT7//PPswgsvzPbt25ctXLgwdzWmGyzUxrSA3jI95I8//jh3mcvKlSvD3rJlS9jGdImnPoxpAQJ8zjnn5L/+yxtvvJGdffbZ+S9jusVCbUwDTHsw93zSSSflLnNh2gPOOOOMsI3pGgu1MQ38+OOPYZ9++ulhF/nyyy/DPvroo8M2pmss1MY08PPPP+dH5fz0009hH3XUUWEb0zUWamMa+Oyzz8I+/vjjwy6iZXhnnnlm2MZ0jYXamJaULcuDPXv25EfGTAYvzzOmAd4yhKqq0nTemHFxj9qYMfjtt9/CXrx4cdjGTAILtTE1aP65Soi1IuTUU08NexoQJl7A0Us288XLL78cYdDyRDM5LNRHOAzbMcuXL89dhof/6jqHG7/++mvY0xBi1msjfHV5wos3l112WTy4nO+3IFetWpXddttt2R133DH0BlRsbqV4soeKqWckoU4TGXPuuefmZ/ZDC5uex78xhyN///13fjQeiPTFF18cbzcy171ixYr/vAlJvbrhhhuy1157LUSyD1xwwQXxWv3WrVuHEtx77rkne+mll+L4/PPPD7sONAYtaQvpOQkYRdBoExZ2SSTOmv6aKDxMHIXVq1fz5OSAGSR6fmY//MZ9UOByFzMfbNy4MfLh8ssvz12mi8rH9u3bc5dDiw8++KA2/bpKX/6/ePHi/Nd/2bdvX5yn3vUR8nfYfJZGELc65A/TliVLlkR6rV+//t/Z2dncdTyU15s3b47fivM06tbIUx8nn3xyfrSfe++9d07Lore4vP/B/MFc5iuvvJL/mj6Hw0jq+++/z4/qqVq61wby6ZNPPokpjSo+/fTT2Lnvrrvuyl36BT3rgThmjzzySO7SDC8SMfdft9sgmoK2MMIAPTNo4uuvv45ePpCu9MjpDbf9fxHC8dhjj2WDhvLAswHizG/ybtLz9GPPUSsB2QvhgQceiOMmmFvTUAbDUKI4hChOr/CbRNZ8KMOOac7RjRMe/Gq4hOE/ZRlbTJei4TrAsI70SueGuT/zhEpDrk8loHIDhUl+dX/9lhsU3dNzxTQo8yv4z9q1a/NfWWwBKj9puGUUt+K5Oj788MPwQwWcb4odl2F48sknw77ooovCLuOpp54KIRynQZg01113XZSztB7X8c0339Q2ToCmIIbq8OmZQRtIq0cffTTWuT/00ENRb6gT1DHqWttwAg0lGlfMo6uuuirsjz76KOyJkfesh0bDAIaGxx133IGhiYY+GhbgL4WhCO4MSxiSMOxhmIIbdjoMkl8MUyjpfWS6Gta0YZTwKG74J24Mm+Q3HSYqPTG7d+8+MNTlNza/ubbSFaMhWBquYnrLvWx4pmF98Xw61NS9heKjIThhStMhJY1TGlcgPXSOY8G95K74VUGY8TfJoafiUExX0XS+DvJZcU1Nmh4C97ppD9KtLD24B3lIHrUB/7pO8X5yx5Shskm5KoKbyg5hUboVp0xTuB5+iZv8F8vRsHAtylVaL5vKGaiOFe+vOE+yDMLYQk1AdYwhAUARSAtwWjDTxEkFI804XQNDhimR0gJTVigmxbDhIY5yJ+6C/+KWVki5Kf0gTVfdS2FI/SGW8lcsMFXuouq8woOdgj/cUvFO459SFn6RloWiMOFWFd4UlZu6yj4uikNajlMU96rzbSD+xXROUZ7X3QMhIU3VyHJMuSB8aV41If+INNdJOx6441aVN1XhVJhw5xoYCWVaL4rgR3mrulQsR+Og8GKaUD6X3R/3qjTpik6W5/EEd9Bqx/HOnTsrpwAYFokTTzwxP8qyK664Ij/KsnfeeSc/msu6detiTgguueSSsKHtHGLXtAkPT+dFug/E0qVLw2YPY8GwCpq+DsI9B/kWc3BiEsNhzcMRLj1BZ6j41VdfRdzH/YoJ6aEyo7lE0JTQ/fffH3YdlBvSYpIrILTPxyQh/k1TAE0wxCdNL7300vj95ptvxlTYQByHyitWcOBfQ3ryW+g6bfJGkJ+33HJLfJoMneAaGMW3an8UTWcpb6UXP/zwQ9ijQhnWFCPTcYNGMhs0AvnZ/tLZOupUlCggZcuWplHoi6TznW1Ml6QNU3qP1F0MelRhV82bFTcEYn6WdNacdteoogKVHt56660Q7ptuuil+jwuVBLgm8YHXX3895mLVCB7u0AgS/64eutNo0wBu2LAhu/322yuFsInTTjst7O+++y5sII8GPceh8ua5554L+8477wxbMD/NtcqgDvAA8ZlnnsldDvLXX3/lR8Oh+rJo0aKY77/55pvjs2mI9ny/ONSGzoSazFPCU/C++OKLOJ5v6HENYyZF2b0wgl4qMCKh8lJYtWIDQVOvGXfE+corr4xeNQ9J0ut0Bb1V9XjV83/iiSfiwc4wPbQ6UsF///33I24vvvhitmbNmty1nj49TDzmmGPyo+HYsWNH2Oedd17YXUBDR8OfjlSHRYKPoIpnn312qN40UHYov2mZIZ/prKQj0RQeIKIh6QNojoeFh/08dOdB/oMPPhiN1uzsbNQbeurDlONjjz02P5qLRpuTpjOhhhdeeCE/yqJFL1KVMSlVCXIoQoURTcuCNH2E4SOqtPzA0PX555+PY6AQI+ZAJWhbGUfZ4U09Xgo3qzKwR10e9ssvv+RHB0EMlEb0bDZt2hTxb9vDQTigarpsmlR9VKCJbdu2hV3XS9U57XtdB8LBVApCN66IkDea+mAKg/yqC6dG0frSjaaxiqMFVlBA2Rdx+A+N9e7du+d0aLZv3577aAedGU2vvP322wfEWR2eYVEcilMv//zzT9httG0cOhVqEgFhqSLtNaQRTgvU1VdfnR8d+qTzjgy7JNZq6TGCZWkIIeKjwom4al5PpIKvQtfUCADXJp0xhKUN119/fX6UxVI7etOjFvR33303bO6d5jdDUEBYuMfdd98dv9vA0B6uueaasCdJVY933C1OEdWqKYAURDN9LlEGPVXS87333ovf6q2PCuJEvgDrox9++OE4rkKjaE2blEHea5p02bJlYafwOjrlrDhlowai7fTpq6++GnmjuftxUR6pYRValnfttdeGPTEGgjASeipcfMLLE12eYHOu7Lz+h5+BeIT/Qc8t3AaFMfe1n+JyOCH/RfdJM2x4immRGtzTJ95lfmRIF/lNw8CqB+5Bmg56ouGGTbqKNGwyWnGTrrZRfhTRdTFlT7z5TxrHdNULYZa7DHEhzIL/6xzXSc/1gUEFjbBVrTZQ2KvO16H0IU+b0KqHsjwC0o2wqpyQlvzGnTKQpivX4VwTxAm/5Fmar1VQVorXTcPB9SiraALXxY1VHSqPci9LS8W/qBHTRNqllSiEk/i1yb9xGUmolaAyxYRVomKKQg24keDyw3HRnwpJavBTvLfcJ82o4aFikcESM2x+FyucCkGV4X9A4U796lpUBrmllQX/Osc1VClA/sv+J7S0quwcpPeVSeF+ijt+U8EQakymkY/DorCXiQcozlXn61DathFB0g0hJL+LkK6EM72O6iD/STsEgHtVfqaoES27ZxHVj2I6KP8xCBrxwI/clOdKCwx6kNYPXVtGQllH6r+NaQvhJdz8h7SdVpkduUdtuoOKpIJbFDIKggrTKGJwKKCefbHx6gNNaa/zo6AGqqzxKkOC1UbY6+AabcSXcoloNoVPjcg0epZHKhbqHiAxLuvlpL2JthW67yhOxIdjGqi+VnKlfRVN5+sg3m16tinqobbpVZah9G5qFMkbwtbkj+tV9fRNd1ioe4CGfVSgtLekHg3nDqfeStr4YKjofW2EFMYyCHPd+TrUOJMWw4J4IoyjiCO9+OJUiKARoJxxfUS6yp+g3HK9UeJghsNC3RMo9FQOVXwMwk1FGHeo2zcQODVAbXpt84nyoQw1OMP0iiXuNE59y1eEn7BR5vqcJ0ci/ritMRWwppcXLQZCHK9WF2k6b0xXdLqO2pgjkVHXlhvTFgu1MQ1UvXWmty3H2YvamDZYqI2pQEJctY8HXyiBslehjekSC7UxFUiIm/bxOOGEE/IjYyaDhdqYCrSlZtVGRLt27Qq7i70kjKnDQm1MBWzxuSTZAbHIn3/+2WpDJWPGxUJtTAVs8Vn35RX2VJ7Gzn3GWKiNKYHtONniM93qNUV7LevTV8ZMEgu1MSXQW2Zao2r+mX2IV4+xP7cxw2ChNiaHr4LwWS99Bm1j4SMYCxYsiPP0tvm6zqhfuzFmWPwKuTE5fFtvdnY2PgfGV0iKqz3S83zeyas9zLSwUBtjTM/x1IcxxvQcC7UxxvQcC7UxFaxcuTKbmZmZY3DjYaMx08RCbUwFW7ZsCXvz5s18YCMeJO7cuTN7+umnw92YaWGhNqYCluGBXmphzTQrP3gRxphpYqE2poIdO3bEXh8LFy6M6Q7WUPNa+apVq3IfxkwHC7UxFWzbti2mOpibXrRoUfSw+e3102baWKiNqWDr1q0H5qdXrFiR7d2716+Mm3nBQm1MCdqUaenSpfH7xhtvjP0/EGtjpo2F2pgSEGVQD3rZsmVhb9q0KWxjpomF2pgCbGG6du3aOF6+fHnYPFDkweKGDRvioaIx08R7fRhjTM9xj9oYY3qOhdoYY3qOhdoYY3qOhdoYY3pNlv0fDXwcDYfezKYAAAAASUVORK5CYII=[/img][br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWsAAABYCAYAAAAz39bPAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAA2/SURBVHhe7Z3Jjw7PA8Z7fnfrOJGIGAcJCbFNYktIMBEHEuvFhWQyIhIxdhchgjAHB4ZEMidLECJ2iTlYIrYQxAURwWnsf4Df+5R6KD29vfMu3f3t55NUqru6ut5an66qrq634VcJTwghRKb5n7WFEEJkGIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EELkAIm1EA779+/3Bg8e7DU0NHhr1qyxrn/Zvn175HUhaoXEWggLhPjJkyfely9fvG3btnlv3761V34Dcf769WvodSFqScOvEvZYiMLy7Nkzb/z48d6bN2+8kSNHWte/3Llzx5sxY4bX09PjNTY2Wlch6ofEWogS6DWjp3zt2jXr8i/Lly839qlTp4wtRL3RNIgQJSDCEydOtGe9OX36tDdhwgR7JkT9kViLwoMpEMxFDx8+3Lr8C6ZAwNixY40tRBpIrEXhefXqlbHHjBljbD/37t0zdv/+/Y0tRBpIrEXhef/+vT0K5t27d8bu16+fsYVIA4m1KDy3bt0y9tChQ43th0v0xo0bZ2wh0kBiLYQlaMkeeP36tT0SIj20dE8UHnyNCMKaQtx1IeqBetZCRPD582djNzU1GVuItJBYi0LD+egwMeZKkVGjRhm7HiBO+EiHH+KkxdGjR00cuHRRpIvEWhSaT58+GbseYoz13BA/TKvAtLS02Ct/wcc5c+fONS8z0/5asrW11Vu7dq23fv36sjetgsAznZMnT7auohJSEWvsbMaCjDJ6oou0+fHjhz2qDAj1rFmzzFeQmPtetmxZry8mUd9XrFjhdXV1GaHMAtOnTzef4N+4ccNsdJUU3Pf06VNzjIdPHAg7C20eowk8uBEX7K6IeHEqLHXwgrHe7Nu3D29qfrW1tf3q6emxrr9+bdu2zbjDlIal1lVkGZbX7du3rUu+uHz5son/vHnzrMu/sK6GXU8K7o+q02gHuI42kUVQvuWWc0mszT3I4yjor9zwqw3L+uTJk+acaa607KtFqtMgu3bt+rODGebp9uzZY44Behci22CElHdevHhhj6IJW9aXBNTt69evR/Ywb968aXb8a29vty7ZAj3lSZMmebt377Yu8Xz8+NHYo0ePNnYYmzdvNiMN8OHDB2PXG/Se9+7d65Ueln/eFSDNOEfZZWGUn4pYb9q0yQwF3a0mDxw4YI88r/QkMxnlB+LAIQoM5vzcTPRPr+Acw0/4o5sL5gQxn8ZrCDvJsIf+YXA//HMYFzR0cv3DAMSNm9i7oseXS7wGg8pz5coV6+M3vAaTJA7EP28alGZeowH++CJP0cgItg+lfze/aZhG/7UokGb4wdA0bUaMGGGPyod1e+bMmcYO4uDBg0YMK3ko1JolS5YY4QqqV0HgQYgXt1FpQhtEeJgbB3Ffk9YKPCyxP4y/jBYsWGDsq1evGjtVfnew04XDDRoMi/yUKrK5VnoCmyEjhir07w6d3KkU+B00aNCfcxhCfxh6lno0Jkz+Bmx3esaPO2zDEAm/w3MahE8QvhsPDHVdvxh++f3RzU0nh2eg3DgADvlhkGdumt2hXtL4ctgI4x++uvHBMcFv0t1NTxCIE/y5cas2TAPT5CfuehRuGbnGzQ8C96gpEORbUH7gN1CHUV5JgH+G4/89usMEwXYaNK2BcN0yR9ioW0FpJUgT4o1wGXZf8rkaUA/89ZjxqmUdTEomxNqtJEEV1hUsVApCQXErBDMXhkKMe+gX4Jx+XMFwxayzs9O6BkN/rl/3fn/jcdPICkkR5DkrO+LtQkH1h8nwYJLEAeHC3c0v3Ef/bt4miS9s+vFXcjeP/Q0WbkkqP9MSVxaVwDQwTX6YD2HXk4D0+8vCJYlQQUyQpywvHKNuI35RHQs/9M+yRBiED9KwsgmLJ9yRPqST4TH8qLJDmlg3cF9Q2GGwXJIaf/30w/CC/ME9LE/qSepi7RcXt/IQt2BcgtxZoWDCCh7u9OMvHLrHFQ79wbhQWGHcsMPS4MLr/t8Oiy/dYFyC4hCWL2HuSeIblY+ADwdXqPh7Qf7TgOl00+4Sdz0JFLIwmCdJfoOiBqFD3NwHbDmw3flHN3ALK5ugeLJ3jDrnwvDDwkK8/e0d/qPyqZawnIPiC3dcT5vU11mvW7fOHnneli1bAue3ME9G3PlO170cuHFPLUiyTCmIar7ACIoDt/kEmGtmHmKuuVaUGp6xMRfIOfcTJ06YudmgdxL/RbhXdrX+uADto/QQNC/j0Xb6urkUX/o9f/7c2ABlVBKlssrm7NmzJn07d+60Lr/hi9uwsFAHg9r7t2/f7JHwk6pY48VR6clqjktPWW/VqlXmOIrSAybQZIUBAwbYo/SIi0OpZxSYh3jxW03c8rx06ZJ5kXTkyBFvw4YN1jWaLL1g7Gu53r9/39hTp041djXAww7tZf78+dalfCj6jx8/ti6ed+jQIW/Hjh32LBnnz58PjMuZM2eM8AeBl4roaLmdBpg0GThwoD36Fzxss0JqYo2Gu3XrVnvmeYcPH/6zOgQZhMJjbxOVk/Dz4EqYPXu2PQonrPDi+P79uz0K33IziKS9mSR7KgfFwf2XE+7PXE2CllxBEFh2aKDHjx83AsGlUXFAPAAEIW3C/pggju7ubmNHlS+vJSkXtA18oILebKVCgrJ58OCBOUZbQ3lFxZMfCLl1CaI7ZcoUe/YbtNFHjx4F/k0a2j1WO3V2dvbqLJRD0IqjKBM3cuXI5+XLl8YmP3/+NHYSzag1qYk1Gi4qHPA3YPZGiDus5x+bAthYdgZTDm4vxy0ct/IvXLjQHpUHGhJAmvxDvDjYE2EDIk+ePDE2wkwy7A2KQ3Nzs7EBerfup8zowWL5XyUPwgsXLhgb5ePm4+rVq42NskZPauPGjeY8CZwiW7RokbFrSVjPt9LtUVEWYT1MFwjnw4cP7VkwEDrk58WLF825v52UCwSKbRDrp/HdQxR37941dtS6acSRSxWnTZtmbJeOjg6zBDToC03kU9KpTXxV6Rf7KBPXGWIZ8eFKuGRv8eLFxk6VUkLqDl+S0OBlBME1vHiAOyf7+RLDvYcG7u5LFi7BgSkVgHXtDd9W4378Jn4DLzfgVmo41lc4/A0YvqRxV62EpQkm7qUL/CAdgC91/GECusPExQHgxZB7j2uQH6Sc+LphwCDvkJfELWuE6V7LAqgjiFtYGhn3sOtRMH9YllGw3JBfQSDfEFfWdeQlzllv3XxFOFF1n7Buocz8dSWI0sO/V7j4bcQF8YZBPWJaECZ+w1+Xg16kuvUkrTriX8GC+CJtScqvHqQi1lGi4Rq3gbAiUERg49yt3KwMrgmqGATXUFHpF8dR/l3c30Al5jEqsxtvADfXP0wYaIxsAPAHG+dspC5ueHFxIGhI/jRT6Ek58cW9jCvuC2pofAgmzdt6wriH5RfTH3Y9Ci6zSyKEyDeUofvQJMhXxNMNh4KIe/x1A+64Jw4KZNBv+mHb8ucDfpt1D+WMMJkWho1z3OfWaX84cKdBOGmBOsp4Ig1ZqrOpiPV/AbdypUUW4pAEiAzi6D5YswLzL0yMK8lfPqSS9hQpiEnEPQqEkUSAIbR4WMfFj+KblR5mUZFY9xE2Ypi0yEIcgqDouD2qrDb0uPyrJH+R7iQ9XBeOVKI+JomC+R33YETZIG5x/hAehDqJ+IvaIrHuA+iRsBHDBE1R1JosxCEMijUNGnvS3mW9YRyDQJyjrkeB4TPuQ16UCwQU4tgXgQybMgN4EOChifAh1HF1Bg8MhNeXNIjqI7HuA2zArqk3WYhDGBA5zosn6b2lCeKInmgQfOiU0zumwOMBVel0RrWB+CNunFsW+UJ/mCsKC9be4gvOkhibpWB+4q4LUU9S/9xciKxT7np5IWqBxFoUnrCv0/hVZiV7WQtRLSTWorBQjMP2/eBG+O7n1UKkhcRaFBaKcdy+H8OGDbNHQqSHxFoUFm54FbZvBPdk6es2pEJUE4m1KCzYHnSSs6OjH+ytjJUgQmQBibUoLNjdMOrPIrADXD12/BMiCRJrUUiwjSu2B126dKl1+RfufzxnzhxjC5E2EmtRSNBrxhRH2Hw09jFua2vTGmuRGSTWojDgDxbwF2HYIP/YsWPm781csCk+rqPXffr0aa+9vd1eESJ99Lm5KAyjRo0y//nZ1NTkdXV19VoF4l4/d+6cVoGITCGxFkKIHKBpECGEyAESayGEyAESa1FY8I/6DQ0N/xi44QWkEFlDYi0Ky6lTp4x98uRJ/HODebn46NEjr6Ojw7gLkSUk1qKwYIke4IcvWFONFSH4WEaIrCGxFoXl/v37Zm+QxsZGM/WBNdb4BL21tdX6ECI7SKxFYenu7jbTHpirHjJkiOlp41zrq0UWkViLwnLjxo0/89XLli3z3r59q8/LRWaRWItCwo2cpkyZYs5Xrlxp9guBYAuRRSTWopBAmAF70s3NzcY+fvy4sYXIGhJrUTiw/enmzZvNcUtLi7HxkhEvG/fs2WNeNAqRNbQ3iBBC5AD1rIUQIgdIrIUQIgdIrIUQIgdIrIUQIgdIrIUQIgdIrIUQIgdIrIUQIgdIrIUQIgdIrIUQIvN43v8BoUllNBioI1kAAAAASUVORK5CYII=[/img][br]where [math]R[/math] is the union of two non overlapping sub regions [math]R_1[/math] and [math]R_2[/math].
[size=200][b]Area of Region[br][/b][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAASQAAABQCAYAAACwPQiPAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAuqSURBVHhe7Z3bi05fHMbX/O6RwxWT5OVCiMapMHOhHMIFJYNxochpSpGMHC6UhFxJMaLkwiEuJGdFIckpitwgSa6c/QF++1nv+r7vevfs8/vumTXv+3xqt9Y+7/3daz17nVfTPw9FCCEO8J9xCSGkz6EgEUKcgYJECHEGChIhxBkoSIQQZ6AgEUKcgYJECHEGChIhxBkoSIQQZ6AgEUKcgYJECHEGChLJxOHDh9WQIUNUU1OT2rx5s9laZvfu3ZH7STSNal8KEkkNIsPLly/Vjx8/1K5du9THjx/NniKIID9//gzdT6JpZPuytz9JxevXr9XkyZPVhw8f1OjRo83WMo8ePVKtra3q27dvaujQoWYrSUqj25eCRFKBvzP+yLdu3TJbKlmxYoV2L1y4oF2Sjka3L7NsJBWICFOmTDFrPbl48aJqaWkxayQtjW5fChJJDLITKLsYOXKk2VIJshNgwoQJ2iXpoH0pSCQF79690+748eO16+fx48faHThwoHZJOmhfChJJwefPn40vmE+fPml3wIAB2iXpoH0pSCQF9+7d0+7w4cO160eqnydNmqRdkg7al4JEMhBUHQ3ev39vfKQaGtm+rPYniUGrYBAWZOL2k2hoX6aQSI34/v27dguFgnZJbWkU+1KQSCKk/CIsQkgN0ZgxY7RL0kH7FqEgJQRtQNBKVjo0YpF2IY3A169ftetqhJBvgkVSE/2JvrDvggULSja7ceOG2dq3VC1I6JUsL9Xd3W221hfSfwitZK9evaoePnxo9gQj9ghaEOAgbPUmZn/+/DG+7EBIpJd7WtC3C6mLqVOnxvbxQuTDt8C9+gu1sK8fdE9pb2/X/hkzZmg3DKTg8F0gYnlStSCdPHnS+JQ6deqU8dUXx44dMz6lZs+erRcULMINAh0jbSBgOF6EDMIGgetPohQXId68eWN86REhGjt2rOrq6tKtldMCEULv93nz5pktweBeW7ZsMWvukKd940gi4hhVIMt3SUtVgoQ/DSLf4MGD9frz589LeeF6AQEY75WGsGpbCNj+/fvNWqXQuU7SCBH27lF0dnbq7hIQFESOLOA7IcJMnDjRbAnm9OnTpXtIQ0MXyNO+USD+Tps2zawFgx8n4gDslnfTg6oE6ezZs/ohpQcyePr0qfGV8WdbgD0AlZ10Rn8eXE+ORRYH48MgwNngOGy388G4HnpL+48NAsKJY+0yIdzXn5ceNmxYRYpHjs1Kc3Oz8Sn169cv46sfRo0aZXzJQYdSCUNZh9SQQt/p06drNwh884MHD6oDBw6U1vsbWewbBYSmra3NrAWzZs0adfToUf1t/Kn/WpNZkPAxkfVYt25dxQtduXLF+MrYqSgAIQhKmkMMMBYMrovsDcoFcB4CUEdHhzmqqNg4DtthLGSHJEl5/Phx/ReMAs8OIcWxO3fu1OefP39e33fRokUVQztg3/z5881acR1LVr58+WJ8Ss2ZM8f4+g8uPDN+OPbPBD8lpDYRVqJSEDgH37vWqYxakqd98ePHDx42kx89GDdunHaDkHMWLlxotuSMF7kycejQIcTKf55o6AV+WbDux4vUpf04F2zatKlivVAo6PX29na9Dk6cOFE679WrV3qbJ1Z63RMVvQ480Ssdh3tFgevjONzPBtfDdi9gmy1F7GdPihyPBc8L4Aa9YxRi56SL2LLWyHOEXV9sVO395TphIGzBhvhWYlfvZ6LPibLp9evX9XkSNuGPCydCb3yDvO0L2yBcw1ZA4os/rNvgGOyXeCfxNU8yXx0f1A4AdqSVl7ax9wchIoPFNnrY9iDkuLiAFnacBAosEthB3LMHIcf7F3xgRI7+htggrwgjyHXCwH7YEJFFkB9i2L1FxGy7y3VcIU/74hyc6w93EHVcNwzEby/nYdbK1xGByoNMWTYpzF6yZInZotTSpUuNT6kHDx4YX3JkaAWA7JyU1aA2Kgw8B5LhKJRLWq7TFzVbnrgp7yPqLAWylatXr9ZlYCQdsNnt27eV96euyHZJ+dHMmTO16wdZ+KBsR2/UGrkAys1QROF/f5QfhWUREU/u3Lmjtm3bZraU+fv3r/HVnkyChMJssHLlypJwbNy4UW8D1Q6v6SkxfpE9lh07duj9KEOACKG859mzZ2rfvn16v8ughzbKLwAiAsre6pFBgwYZX+2BGIHly5drV7h586Z2g5phoLwQPzicK2EVi1yrv5HWvhCWoPAmlTdhIo6yWZyHSh2xGeyYN6kFSQqz8ZfyC4aXLNbH4EX8tVVx2KPgxVXH7t27t1QVj2dJU+AW1nbITx5jzqxdu9b4in+nJMKNQkU7IsUtdo1lXxA2uFgtkOE5/MNvIAwgBRAEUtBe1qNHWPWyKuaIeFz6BmntKzkP/3nXrl3TblCBtjy/l9WtsBkSCnmTWpAuX76s3VWrVmnXBh9ekBdOit1SFLVfdmSFuCFFJNW04gJJutvb4pDA6G+igKlnAIQ1jzFnUG0KIRf27NljfOEgVWgHirhFUpF5EfZH7auhMaSmKKhBJMINUkJSzW8jWZUkWfje/Aa9YV/ELeQsIOL+ZhaIR8jiob2cf588m128UmtSCRLy8HhYENSy1M6T46WlnAQvaUf+oECAl7cV2M4OImsGQRLxsQdBR6BDFu7IkSOlFBo+XpRA4T5SniMBGs+EPy1AmwvB/+xJUn7+e799+9b4lNq+fbvxFZtD4A9eD+BdqgXfUSJe0PeTckr55viTz5o1q3RvnCPtmbAfZXX4+fir+bHv0qVL2p9Hl4w8yGpf+flKthbxEiNTitjAFgiDYm/4ES/stoXCuXPntPv792/t5oKn6InB4fZi10RJCbx/ASjJD9oeBGroUPovx8Hvr7VDrYlUQWKB3/tgFfeBPwrUFEhVKI6Hi3V/DULQs9vvHYT/eP859rNjge1cR+wU9u7yLnG2CQLfN8jO2GbX8uC7y3EIF3IvfDc5Ht8PYcEOQ2g6YmPfC8fh+L4mT/vChjgXNY1iC2lOY9c+ih2xwG9jx288a5bnSAIHaCOJQEoVeAExsBxO9jM4ZYP2LUJBIomIixAUpOqgfYtkqvYnxAblECQ/Gsm+FCSSmMFWf0QbaZg4P0VVOukJ7UtBIgmQWtGonvQkO7RvGQoSqRku96KvBxrBvhQkkpiwfk8ypEqtx+ppNGhfChJJgESIsH5UMgW03f2HJIf2LUNBIrFIhIjrRzVixAjjI2mgfctQkEgs0lUgrGOy9AHknP7ZoH3LUJBILC9evAjtTQ8wNjir/LND+5ahIJFY0Lk4anoh9Ki3B+gj6aB9y1CQSCQYsQG9v/2DognShmbu3LnaJemgfSuhIJFI8HdGdiGs/ALDWmCMJ7ZBygbt6+MfIT4wJAeGp5DB8f1DsmD4CezHdux3YfiO/gTtGw4FifQAkQD/KrhB497Y+/2RicRD+4bD4UcIIc7AMiRCiDNQkAghzkBBIrF0d3frEQvtBZMuyCQOpDpgR799MbFlkmmy6g0KEollw4YNumoa1c8ocsR8XYVCoW4nu+xtUOWPmXBgU9gXy/r16/XMO402GicFiSQCrYkXL16s/ZhCp6WlpWLaK1Id6K/Wbs1rKHOg5TrlkINQkEgs0ppYJvPEvGgymSCpDZhHH3PMAdh769atjdngFNX+hEQhc3jJ4mXfcpuXqxFBWyPbvmh/5J+LsFFgConEcv/+/VL5kSdOOvsWNCc8ycaTJ09K5UeeOOlZapubm83exoKCRGJBdqKtrU37ly1bprNvd+/e1eukeiD40tsfBdwYikSmrW40KEgkEvQ2hwDJHxsF2ogwZ86c4XxsNQA2hODb42VDnFDlL/PtNxIUJBJJa2trhQsQYdBLvbOz02whWeno6NCC39XVVRpqBIXb2BY1aFu9wr5shBBnYAqJEOIMFCRCiDNQkAghzkBBIoQ4AwWJEOIMFCRCiDNQkAghzkBBIoQ4AwWJEOIMFCRCiDNQkAghzkBBIoQ4glL/AxkIjUObyfpLAAAAAElFTkSuQmCC[/img][size=85][size=100][size=150][br]where [math]dA[/math][/size][/size][/size][/size] is denoted as [math]dA=dxdy[/math] or [math]dA=dydx[/math].
[size=200][b]Volume of Region[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARoAAABbCAYAAACswErHAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAzMSURBVHhe7Z3JaxVNG8Xbb695HVauxAEUBUGjgtNC0KgRUTBExYWgGKMrEZxFxAHjRhCcgoIEY4wIiuAMCk44o6C4MBEJ4irG4R/wu6fscy073X17jEnu+UFRffv2XFWnq556qnrArwKOEELkyP/cWAghckNCI4TIHQmNECJ3JDRCiNyR0AghckdCI4TIHQmNECJ3JDRCiNyR0AghckdCI4TIHQmNECJ3JDRCiNyR0AghckdCI4TIHQmNECJ3JDRCiNyR0IjM+Pr1q7NhwwZnwIABJkyZMsX95w/cZsiQIWab0aNHm3WifyOhEZkAsRgzZowze/ZsB5M21tfXO9++fXP//Q22mT9/vjNixAinq6vLaWhocNrb252hQ4e6W4j+iqbyFJmwfPly5/v3787NmzfdNd3ZuXOn09ra6rS1tblrRLmgGo1IzZs3b4yArF692l3THdRmDh486Kxbt85dI8oJCY1IzcWLF008depUE/tx6dIlE0+fPt3EoryQ0IjUoDYDRo4caWI/7t27Z+Jx48aZWJQXEhqRCjSJYNCtqqpy1/hz+/ZtE8vwW55IaEQq3r9/7y4F8/HjR9MDVVlZ6a4R5YaERqTi8ePHJg5rNn358sXEqs2ULxIakYofP36YGL4xQVCMRPkioRGpePnypbsUDMVo8uTJJhblh4RGpCLK8AGKUUVFhYlF+SGhEal48eKFieUfI8KQ0IjcuXXrlrskyhUJjUgMuq3joFpP+dKnhAb2gIcPH5og/j3sthaiFH1CaDC1AOYuGTZsmDNr1iwTRO9i+PDh7tLf5PlSuH79ejFvMITVsvCiOnXqlJkDBwNBexMY/Y55etI+r8OHDxefBeb86S3EFhpvwjJgvU2p/+PQ3Nzs1NbWur9Eb+Hz58/uUrjDXh5gyonq6mpn6dKlZv6bkydPOoMHDw68DgjLtGnTnMuXLztnz551Jk6c6P7TOzh27JjxRVq8eLG5t6Rs2bLFaWlpMcthg1y9YJIylNPcXgyYjyYOnZ2dvwqFHnPYFAN+e2lvby/+X1lZafZLQ0NDw1/nFP8eO02CePDgQXEbLGcBj1lfX++uCef169e/CiIUeft/SRbXeu3aNfN8kD5RKIh05mnkJXaNBm7k27dvd3/9ZtKkSe7SH+w3y+nTp+V+XqbYtZ6sRm6fP3/exIsWLTJxKdauXeuMGjXKOX78uLum94Ka1rlz55wTJ06YpmESHj16ZOIoxnc0J1Ge8x6HlshGg4eBhCOvXr1yl/7AtjJuoLdVU0XP0dHR4S5lM9YJVXsUQoCmUClgs4Cvz969e901vZ+FCxeacrNq1apIDpFe6CA5c+ZME4exe/du08Sqqakxv9+9e2firElsDLZtJpiPxPtAONHR5s2bTewFGcaepBoB7URkjDgPF8fh/gxsZ9qGMQYb7388tz3BNpZ5PXjDsC2L6w5rS8Mm4Hd/Fy5ccLfo+3BoQU+BZ2h3BKBzAOtgSA2isbHRvBRReINAujOdvOmDNMb6uHYT+5hYtrHzLLbxA+UGI97v3LnjrukO8yrPAyM3zgW/pSg1FIq2XdPLLU3dJlRs7LY3AtqFNoXENW1NP9tMS0tLcT+2I3E8bI912Ne7X5iNhm1SBruduWPHjr/+s4EdiedEwLb2bwa0l+1rtgPat17sbfm/vS5O+5v7xAlVVVXu3vmC8+B8SK8gothx4sC0RlqVAvYObBv2vJEuSCPkN+ZZgv147d78HYZ9TOYnb36mXcTPvglo4wz6H/fG62V+t/NzlOcD2ynLH9OJv7MmVerbhdJOTIqQXwLbRmI7UYEtCt59w4QG2P/ZQsNrYfDCwoJgJ5p9LViPRMG1M0PyP2+hthMb+9jY+yGj9HX47MKELWuh4fFQmEvBbf1eBn4wzZE22AfpmDadKFZeoaLQ2HnVC/ORH8hbvFYbpkmp54PzIz9SAFlO8hKaVH40dpWVM6gBGuvq6upMbHPmzBl3qXv324wZM9wlp9gO70kKmaLYrl2wYIGJAaqwR44cMQZu2BnCJtjG/fEzI2z3ElRtSbm45fvZ79Jw9+5dE0cxLH/69MnE48ePN3EpmP+QNjCQYvrRtPZFfH4GvH371sQETetCQQ+1o7B8eH2D0LyD3Qn5Nej6wrq20eTC/R09erSb3YzPN2tSCY1t9S+8yYtOUHgQaCP6PQR7WgGvz8OgQYPcpd/Q1tJTZDG62L6/rVu3FtviCOU45gefYAEoVFnw7Nkz4y8TRQDiDpEYO3asiZFusFtk0YlBQbQFFwUdZWT//v3umnC8Hti7du0ysd+LnM8nzK+JBuAwu1XWpBIar9X/yZMn5gHijR5kBLYJmyypP1CohqLe6xvgWBUFW6iihjTOkXlh1+aSghcZ8lbY2zoNLJx4SYYZmONAscKLmKDWC+FNcg6IJ47lJ7Z8PvPmzXPXdIcGYLz07DyTt7d9KqFBtcvufYLX5ZUrV8zy3LlzTRxGqWrawIED3aW+SRYWfD+RKhXCPuKWJXh79iScn3jOnDkmzhr04KAAc+qLrKiqqioeE7WZQ4cOmaZ4Eli78RNb1pj9/NrIpk2bTJPLm2cohOxhzZpUQgOWLFniLv2+UXR140aCfCaizrIWtXrsx8+fP92lv5d7ArvKys+Q9Fdoi8qr4Hu5f/++iSdMmGDiUoQ1H7xgDNTz58+dbdu2md9ZNtt5HahxoDaDGkcUHxcSNI7MhgIGghz1cI8QlH379rlr/sBrzFpkSWqh8au5rFy50l3qjm1khTDZCmo7C0Gs4gBhIk1NTSZGNXPPnj1muaew7x2JirckbQWI4ecAf5q49gPhGCEAtKWUgk3zUk5oaO7DOAoPdhbSsHmOkYZobnj9Y4LgCxOmBYgBvtgZBdYYowjmxo0bi00mPxFDOcM9ormWheNkbArVptSwqw0BXWal8OvGRjddQSzMOhzP63cAfwLug+Dt1sNx7P8ZbP8VBHu/ghAUz4mArkGel92PDHYXadJrYYji49AX4P2EdYny+abtNkW64Dg4XlSQLtiHecyLnQ/t7mCcg/kY+3q7ptltHjUdbRcLOx+FgbyJ7f38aHB9CLg/PBdcI66fXdtYh2u292WeDUoHO79783MWZCI09kVGfZB8ENwPAQ/Kb38mrDfY8IHzPxwLD4yZzQ58kEwYO+BcXt8bBqyPci3ATngEZAzcb5jfRF+D9xaW5twmKINHhWmCZxoHCEbQyw8vNKSL1+eE+Rn/+V0380DUe6JIxrl2viC91wbwLHBPPCbzFPfBdaMs4LzAmw+DhJMBx4bQZUkmQiPKD75xEcLEk9ukFZq4hZtwP2/hSgNfaFHf/LgGFPA4hZciSLHo60hoRCJYw0CIIjRpCzrfykmq9WG1mriwuR1V8FjLiHP/YbWZvoqERiTCFpqgws8mA0KYGJWCx0kqFrg+NifSAoEpJTK4Vlwzm2BxbHJZXmtvQkIjEmELTRBRxCgKbKqkESucH0KFmlHW9gcb+54R4ggGhAki0186C2xSd2+L8sSe0CoKSXyiMC0HupHRrV0owLF8T7zg/E+fPjVTf6IbmMNlsoZ+WwVRM9OLRp1sC93OuKarV686Bw4ccNf2HwZAbdxlISIDHxKMCSrUEAI9keH0Btf2wlva6erqcteKckQ1GpGK//77z13qDp3e8hqbJPoOEhqRCI5GDhtXQ+IMBRD9EwmNSASnfwgbd8T5YPr7KH1RGgmNSERbW5uJw8YdcTyXPoUrZAwWiUBvUCkjLybNxgjvzs7OfzOQT/QaVKMRseEUCmETN6E2A5FBr5RERkhoRGxu3Lhh4rAPuPEzIfBbEUJNJxEbTstJO40fmHOnvb3d+fDhg2o0QjUaURo0kTgPMWdp806sDQc+CBAmWOIs/ZitTiIjgIRGlARd2ZzMev369cbu4rXPYH5kCBC+HrlixQozwfeaNWvcf0W5I6ERJbHnea6vr3eam5vdX/7U1taaYQmqzQgiG40QIndUoxFC5I6ERgiROxIaIUTuSGiEELkjoRGJwIfx0N1tB/jRRP2omigv1OskEgPvX3Rhc4Y9OPPBzwZTWNbV1Zl1QgDVaERi4P1rf3eb4gLnPSFsJDQiERzBbc81w/lnKioqTCwEkdCIRHA+YH6ZAF8sgEcwhh4sW7bMrBOCyEYjEoFBlhj/ZNPS0hI6R40oX1SjEYmAyGDcE95Tr1+/Nus6OjpMLIQXCY2IDZpJgBNf4eNsaDI1Njaa30J4kdCI2DQ1NZnYnpi8pqbGTBNBERLCRkIjYgGHvNbWVrOMWgzBHDWgurpaYiO6IWOwECJ3VKMRQuSOhEYIkTsSGiFE7khohBC5I6ERQuSOhEYIkTsSGiFE7khohBC5I6ERQuSM4/wfQL33ZrBktoYAAAAASUVORK5CYII=[/img][br][/b][size=150]where [math]dA[/math] is denoted as [math]dA=dxdy[/math] or [math]dA=dydx[/math].[/size][/size]
Double Integral Calculator
Take Note!!!
[img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAXkAAABICAYAAAATUoWBAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAA4zSURBVHhe7Z3NqxfVH8fH317Dh5VERBYkJkXcHhYpdBeZJpG4MKxFUFS3RQuJjGsuAgUVQRDxIRREkPIJWqRYiwR7gKIiqWijLVy00sz6A+5vXsf52Nxx5syZ7/fMvd+Z3i+YOzNn5vuZuefzOZ/zfGbOVEoihBCil/wv2wshhOghcvJCCNFj5OSFEKLHyMkLIUSPkZMXQogeIycvhBA9Rk5eCCF6jJy8EEL0GDl5IYToMXLyQgjRY+TkxR189dVXyZw5c5IXX3wxC2mXZ5991j3v999/z0JE19i1a5fT4ccff5yFDI/ZxaVLl7IQMQhau0aUsmXLluSee+5J3njjjSykPUjETz/9dPLnn39mIaKLLFiwILlw4ULy8MMPZyHDcf369eSBBx6QXQyJSvKilB9++CG56667kvvvv98l3nPnzmVX4oA8ZFNSW79+ffLMM89kV0RXIHO20ja6hFgOHn777TdnFxQ4eAbPEs2RkxelfPbZZ8nPP/+cfPvtt8nExERy7Nix7Mrw0Bz08ssvJ0ePHk2oSM6fP9+V5EV3oJSNztatW+d0uGHDhugZ9TfffJN8//33yerVq5Nr1645m1TTTXMaO/l8CazYZkt7HKU+rpH7itGmSpc44SVLliTbt29PFi5c6Er0g1Alf9++fcl7772XPPXUU1lIkjz55JPZkRglqnR4+vTp5PHHH5/WnDdIRu3zJ1988UWybds2ZyfYoRgQ2uRD+emnn6bSUtfUlStXpj766KOpVatWZVemps6ePTs1NjY2lea4U5OTk1M7d+7MrohRxKdLdIcODfR68ODB7CwMn3zM7ssvv3THdp8YPXw65NjSOGk+LRS4+5vgkw/YCbIB/yI7GYxGTj6tklU6b5SMIkQ38OmSxGZOnnvQrSW2UHzySbzYComb+3geCd4cvxgNQmwEu+Aec8g461B88rEFk4mdYINNCxriFsFOnsjOl8DymEJEN/DpEkhQbNxjDrgJdfJxDlwnkVtpbmJiIrsqRoE6HZJJc51aHjpkbzX5EOrk4/yxPe7BPqoyA1FP8BBK2s6ee+4518lShDGyH374YXL58uUsRIwyPl3GoG35on1kI/0huOP1l19+yY7uhA4SOk9EN/DpMgZtyxftIxvpD8FOHkeeVseys+moBN8tfLqMQdvyRfvIRvpDsJNnXGzVMKYrV64k4+Pj2ZkYdXy6jEHb8kX7yEb6Q7CTZ1JCGZqc0D2qdBmLtuWL9pGN9IdGk6Huu+++7Ohf/vnnn+xIdIkyXcakbfmifWQj/SDIyVtp/d5773X7PH///bfbDzorMgRWJ3zrrbdmbBbtoUOH3PP6uCqiT5cxaFt+FbKReMhG4jAqNhLk5H2ldeslX7Zsmds3haFUjz32mJvWzFaMEAyCNTE2btzoptnPBEzV5nk81wyyDtoY7X+IudxqbNquebUhHx0w5b0qfmUjcZGNxGEQGwHzh2QQMWjUXBMb1khhrOwHH3zgFiCaP3/+tCociYL1MFjIKr/OyUzA886cOeOeH5IT04l09uxZd7x06VK3L4NMDQXyv4t6zAaWLFnixlSvWrUqufvuu7OrshHRLxuB8+fPu71vRU9ksU4Yc5TqCHLyv/76a3YUFxYf2rBhQ7JmzRqXAIrrRm/dutUtgjTTijGIZEoHu3fvzkL8zJs3z2VUVcrB2N5++213bM1cM01bujRiyz9y5IjbW+mLBJC3B9lIfGQjcWlqIzbqyLdo3+TkZHLjxo3k5s2bWUg1QU7eBPERiSI//vhjdtQMqi8sHUoOVwVVrldeeSU7mx3Wrl2bHDhwwCW+OlgaFWOqAmN8/fXX3fFsTQbx6TIGMeUT58ykprpbhWwkPrKR+DSxEavBVRUEuP7XX3+5GgvffaijUXNNvgpk8LCm0PHxyCOPuOM333yztA2Nf4ScqixBkEFQVWGzKhC/57wopwi/taVN89Vh+/hBsR3siSeecHvWVS9Cx4rJ4venTp2qnC/Ae+7YsSN59dVXs5DZpUyXMRlWPk0WixYtcnMwTpw4Uaobn42QmKxtE1lguq9r6+S3Zg/56rB94q44u1s2MhiykVvwjvYe/I6luHHgVZBhvf/++9lZAFMB2CpzZYsJpS/jroUuTGSwWp3v8aw4V3Wdxax4HgsXcR/vFbrAla2cxwJcLJBl2IJJZavoEV5cIAk5PN/ixN63asEl4slkl8krghzuC9ma4NNlDGLKZ/VBnyyfjZieiXf0bMfs60Aui25hU+g4z9jYWKmt8R6ykTBkI/9iC70hD5BZdp9BuMnmXdnqCNI+kVEVkTykKhJ9IJPIqMIMwQeKCf1Hi/B8HL2BseTP8xQj3QwrnyFYgiszEBSZl837lhnBTODTZQxiyrcEUJXoQmyExEPcE+forQn2/PzvkFUmh/tkI2HIRv6Fe4t65j7kFkEmGYrJRlbeZqoIaq4Jafdpyueff+6qKMNAez7t+vv3789Cwlm+fLmr5hnffffd7bbQOmg3TSPXdaYYtLWyFkdxqjbVOjrS6NnPE9rTHps2dJknpvyvv/7axXMxTptA5xV6porbdPLNgw8+6PZ//PGH26MzqtMhcmQj1chGbkETEc995513spBbTTdgzTt50szRfVEtLzvvw6oYegglTrYpGDXTmleuXJmF3EnI5CrrwBkEG8JmkfrJJ58k7777rjuuAyMlseZhwaWyTIvEjiJWrFjh2tzYQuKM97L767a+QkHA16EWYiPDjMkmMaUlJ+ecAV2GFihkIzNDl22EjnV+m3fayCnLtNA1/Q6bN2++rVOOQ2jk5BcvXpwdDQdfYQffWGGbXEVHSBn80+bkKYU3xXquGaZGjvrCCy+48yJkSPDQQw+5vfHoo49mR7c6fUmUxUyLXB1FpNVS6ou3t7RamN1RDcO98r/xbYMQS5dVxJBPQaBqhAHU2Qi6Y5gu8X3x4sUstBl02GFnVqouK6HJRgZDNnLrtwbvSMd7WaZFLWPnzp3TdMp5CI2cfNnLAzlPEyzX8ykHAyaXswwhD5GBYhgXi3IohROWn65MLze93z74LdW9Tz/9dFq1Oo/1hherT4ySADIIy2wYA81oCuupp4d+YmLijvG5KHyQjCkmVbqMxbDyrYblm0ntsxHi+KWXXnKlqvHxcVfiIxHm9RxiI/yWUjljnDdt2pSFTkc2MhhdsBGrLfkYxkbI+HkP/NfJkyed0+d9ea6N2rF9saXBbKoqA7tNmiPUkjpD1xlQBuFcbwL3h/yGDonifWmGMu0zY9bxwX35zhc6Jeqegfw0Qr2dLdzDlsc+WcdmHSm8E+fW0UanMO9FeF6+hbNZj/pMQpzw7LaIJZ94DZFTZiOmV/QExD/n2I6FQYiNoM+8XsuQjTSjSzZineU+BrUR/BW6Rz7XOLdOafaA/jlHfr6j2sLZsBcfQTHNP46wMgivSyhF+I39Ez74p4v/XChEXl0C4R189/Bcnu/LBLqGT5cxiCUfm0KHdbRtIxQifIlINtKcLtkIPqLOiY66jQTFNAopc+REHtfqIiEPuSS/KRsiVAb3YxRNFESOaqWnKpBbzFnz8Dyem8/V+0CVLmMRSz6JIqQgAG3ZCPaNbbMvQzYyGF2xEZyyT//QBRsZysnzD3CtLrHkIUJCct88RDYOOVShVRDRyGHP/1OlGEp33Nen0pnRhQRM/Dct+cSyEcA+sQ3+j6rEKRsZHNnIzBLs5MtK602dvCl3tnI1Sm+8AxFf5eD7TpUuYzGsfOyDkk9oTS82JMjZttPZRjbip2s2Uuvk7R8qc+Tm5GcrskUzfLqMQdvyRfvIRvpH7RBKm8lVtmKcLRnKsDAx+vh0GYO25Yv2kY30j+Bx8mUrxtk4zeIYXzHajPrqgmL2kY30h1onb6X1MkeOkx8rTN0Wo4tPlzFoW75oH9lI/6h18levXq105MzyGnaRMTFz+HQZg7bli/aRjfSPWifPVN/XXnstO5sO06754onoBj5dxqBt+aJ9ZCM9JOuALcV6wtkXYUQNw5hEN6jSJaMcGG/MNYaEMbZ3EKrkIw874Vqbw/LE8FTpkFF0aenbXcNWBqVKPsMQsT2uYSs8S8SjtCTPgjwsmsOymakTuL2QEIvm2Get9u7d6zYx2lTpElj4iEW0WMnv2rVrbrEk38eDy6iTf/jwYVd6Sx1FFipGDZ8OSfPPP/98smfPHgqEWWgzfPIJ57sQ69atc/LTgkDjBQ9FDc7VF7CSXXFmGDku4VxPlZWFilGFElOVLoFrlNKAyWFNS2lN5IvRpE6H1L6GSet18qnpUYo3uGfQ2qQoZw5/UgWI/xiU0PhIhamf5W8vXLhQ+yH0UIryRTehFE4trK3RMCz1PD4+7pbRpVTPUrxnzpzxLkMumhE8Tl70ExIWDplmFT5ygZO3jx8Mw9y5c90e+Wys0c1edIu0FO4+rAM0v9k6+DFhKDa2QXNOWvJ3Y+gpdIhIUJL3QXWb22yj6qWmmn5gnWnok450jsuq1IPCGkHIpDNNzTbdxNZ7It230Yxidoct0hzMHnv5r64b1AZBzTX5KpVVw1MlqEolhBAjTlBzzeXLl29/m1Az1YQQojvUluRpn2VIE0PsYOvWrS7s/Pnz7lwIIcToUluSt48JL1q0yG10xBw/ftyFCSGEGG1qnfzFixfd1+Qp8E9OTrr1ahYuXJhdFUIIMcp4nTzDmpituHLlSne+evVqNyvy0qVL7lwIIcRo422TZ1zs5s2b3bHdtmDBguTGjRua5CKEEB1AM16FEKLHaMarEEL0GDl5IYToMXLyQgjRY+TkhRCix8jJCyFEj5GTF0KIHiMnL4QQPUZOXggheoycvBBC9Bg5eSGE6C1J8n8W6znsLP0nAwAAAABJRU5ErkJggg==[/img][br][size=150]When you change the [b]function (pink)[/b], both upper and lower integral expressions update simultaneously to reflect the new integrand. However, the [b]integration limits must be adjusted manually[/b], they define the [b]region of integration[/b] and are [b]not auto-updated[/b]. These limits are visualized as boundary curves on the right-hand graph, and the shaded area shows the region enclosed by those limits.[/size]
[u][color=#0000ff]https://www.geogebra.org/classic/ygf7wecq[/color][/u]
Polar Q1
Type "Polar Q1" to find in app.[color=#0000ff][br]https://www.geogebra.org/calculator/pxnzztkh[/color]
Question 1
A piece of solid is cut out from sphere x[sup]2[/sup]+y[sup]2[/sup]+z[sup]2[/sup]9[math]\le9[/math] by the cylinder x[sup]2[/sup]+y[sup]2[/sup]=4 in the first octant. Using polar integral, find the volume of the cut-out solid.
Introduction of Triple Integration
We obtain volume of solid, G, by using triple intergrals in Cartesian Coordinate (x,y,z), as follow. [br] Volume, V = [math]\int\int\int[/math] dV =[math]\int\int\int[/math] dzdydx[br][br]Note that dz,dy,dx can be in any order
Type "Example 2.18" to see the graph in phone app[br][u][color=#0000ff]https://www.geogebra.org/3d/hkm6zzxm[/color][/u]
Example
Use triple integrals to find the volume of the solid which is bounded above by z=4-2x-y and below by region R in the xy-plane: [br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWgAAABOCAYAAAANZ4xKAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAABWVSURBVHhe7Z0JWFRVG8dfURYFFRRFRQXcUTP3pXJHyu1LzSU33Jc0QU0rNRMty6XcckvMJfc9y1JI0dRyQVPUMivAFRBBBREVTL/zP95rAw6b3Bnu0Pt7nnmYOffCnQvM/7zn3U6++4nxj4lhGIbRHVbKV4ZhGEZnsEAzDMPoFBZohmEYncICzTAMo1NYoBmGYXQKCzTDMIxOYYFmGIbRKSzQDMMwOoUFmmEYRqewQDMMw+gUFmiGYRidwgLNMAyjU1igGYZhdAoLNMMwjE5hgWYYhtEpLNAMwzA6hQWaYRhGp7BAMwzD6BQWaIZhGJ3CAs0wZmDlypXUtGlT+v333+mnn356+lxrYm/coA7tO9CQIUMo6d49eQ1cC9dnLA8WaIYxMRBJB3sHat6iBQUHB9ORI0fo0KFDVL16deUM7TgeEkKzP5stnyclJsprtG/fnho1aiTHGMuCBZphTAxEslv3btTGy4tCQ0PJ189POaI97dq1Izd3dypcuDDFCGsaVnTFChVNMhkwpocFmmHyGIUKFqRC9vZ0Qwj077/9RjVq1lCOMJYGCzTDmAH4ndeuXUuJiYkUcvw4/fDDD8oR01CxQgU6e/YsRYRHsPVswbBAa8D9+/fpmx07qG27tvTiiy9Sy5Yt6es1X9PDhw+VMywf3Mu0j6bRB5MnKyN5h5MnT9DgwYNlgM0U4Hf24969FBAQQBUrVaLZs2ZTwwYNlKOmoYIQ6E2bNrH1bOHku58Y/1h5zjwniJD/cf48TZ4yhQra2dGWLVvoiwULaOGiRVSnTh3lLMtmT2AgTfP3p1ZeXvTxRx8po5YNJtYlS5bQmjVrqHbtOvTFwi/IvlAh5ahlA4sdNG/eXH5lLBO2oDVgwIABNHPWLHKwt6f8+fNTzZovkEup0uTk5KScYdlEXouknw4coG7duysjlk9KSooU5zZtvGnUqFHi72ZF+fLlU45aNsgaQaYIi7PlwwKtIXADnDp1ipYuXUKj/fzIzc1NOWK54J6WfxVAvXr1IkdHR2XU8rG2tqYxY8aIyTTvuACQsYH857lz55o0U4QxHyzQGgGrBb7nQYMG0e34eCrhUjJPWGQ7tu+gsmXLCyGrqYwwegXZG/Bz44HnjOXDAp0NEEx64403ZCAQ1tc9YbGoIFKO4oP9+4OpfLlyNOrtURQW9rdyVN/A8po9e7YsZsADy2OA9x8Sclzm8BpONuf/+IO2bduuvNI3cbGx9N6771LdunWlO+Ovv/5SjmQd1TLF3z29h5aVgYhpGLuG4YMrA/8bcJAwi5w9e47mzplDU6dNpTNnztDOnTtp3vz5Ri2Vq1evCkt6IA0ZPJS6duuqjOoTuDBmzJxBpUuVoS5dOtMoX1/xvgdL/+XUqVNp+3bjQjx69Gjpe9czdxITaeLECdS+fQeq7ulJ77wzVtzTtGfSziB2v/zyC81fsMAklicENT1QuKIl5rwWY3pYoLPAP//8Qx988AGVKVNGBpQy4/r1GCFe/WnkyJGyzFbPnBEf2ilT/GUGQ9myZZVR40DIwsLDLSaLY/eePbRu3TpavGgRFSlSRBl9FlMLNMM8L+ziyAJxcbEy6R+5pcZAnqu//1S5FIZF+t1330qXQO3atZUz9MvJX38lewf7DAVMBUUWD8Q9YsLSO48fP5aumtIuLmRvb6+MGgf3ExUVRYl3EpQRhtEHLNBZ4Nq1SIqNjSUHBwdlJDWDBw2iR48fkVerVtSwYUM6dOgwffb55+Tq6qqcoU8gTCgFLiisxgLW1sqocSB2qITbFxxMmzdvVkb1y507dyg8LIxsxb0h9dEYWzZvoVdfe5UWL15MV65coa5du9PAgYPo5s2byhnaoXaVU33Iap6yKcE11K52jGXCAp0F8IE1DAimxd3dnaZNnUq/CBH7VVikq1evIs9q1ZSj+uX+gwcUd/OW8ipjmjRpQseOHZP317NnT2VUv9y7dz9ToUXwM3BPoLwn+GcPHvyJVqz4iooVK6acoQ2oUETq247t2+V1FixYICsLTQmuiQkVTZNyA6wqMRHVr1+fjh49poxqh+GEN8p3FD0Q/8umwDBA3NrLi8IjwpUj5sGsAp02Om0YiU5rYehp5r98+bK0wtKzxCyVe3fvUsz162SFIg1lLK8AtxSsaOsCBZSR3MO5RAmZ+oavAKuRXiae5DZt3kR9+vRRXmWda9eu0YdTptAUf39l5PmYKr6/bdu2VLx4MSpbVvuVJAK9Cxd+QUXEBFSlchWytbVVjmgLYhKfi9UwsoBKlypFzsWdlSPmwawCDcvLu00b+bxfv37k4+MjnwNPT08aO3aMfI5Zd8ann+omYAPfK/yYWltWuQ0s6JSHyVSiREnp5shLwKJCtWD58uWVkdzF0BILCwsjdw8P5Yj2wLWBatYSyoSQFVRh7tixI+385pscxxlgzMBt5upajpxM9LmxtrYhypfP5M2gcB8FxESP/yVzr0jMKtB2dnZUq/aTNKB69eqlskgRVLOxsZUiOG78eCrubN6ZKiOux8Qoz/IWCQkJlJSUN/2TuLeM3FLmBsYGrGi4OFyEJfbJJ58oR7QFro1z585mq8wbueGfCoOoW9eu9MMPuzWJneB3f+NGDFWtWsVk/U3gwrK1tSOPCqab7MD9pCS6LlaadevUlTplTszugy5fzrhFEx9/WyzLNtOAgQMswn/LMM8L3BtJd++axIX33a5dtGxZgLTUsWLdt28fNWncOMOgZOXKlWnhwoX0wgsvUIH8VmSVL+eyEBcXRxcjIkxagYq2CqVKuZjc7XDp8mXpLqtYqaIyYj7MLtAq4eGpne07v/2WbG1sqHPnLsqIPsBSD6lleRHVDZAXgVtKL8CqhXtDbWeKYCsa6pvChYfiIVjpeGzYsIFat25NR44eNWnjJHQF3Lhx49N2u6jYDFi+nJKTU8jNzV0564lVPWz4sKdxJsMHKlhPnDihnPksYeFhMhiI8+APRqEUctcN3Q74rG7ctJGavvIKtWjRQgq4imGM6+PpHyujz5IoJs758+fJtg04F5XDm8S9wQVYpsy/K4snRVAT5Xt5++235WuAbKDevXvJnW3gNsopZhdo5Num9XeipHjrlq301ltvUeF0UtkMwT86NsY0/ANn9MC56ocjuzxITpa9NfIienMDaEmMjtxSCA6+9NJLMgsA/48QFny4TQmsc2SOwIKGwJgKCNOHkyfTl19+SZMmTpIZMcuWfUlHjx4hZ+fiqQKE95KSKCY6RhZ7nTx5Uk4ia9eukzGQkW+PlG5PYxw8eJD69+svtKEwBQUFUkhIiKxJgOgauh3QauHB/Qe0dt06srWzpfXiq+pLh596/LhxsklWyxYt5VhaUGA2fNgw8TsLpsVLltDp06fpvffekz8X1rOjY1F5Hn7miq+WU48e3Wne3Hny/YSKc6Mio2jOnDk0Y8ZMuSGDFq4isws0oq34JamgsGPZl8vk7JbV3sn4h9/1/a6nlkJmD5yrRtAZJjcwtGzN0czI0OeNa5uKHTu200EhYJMmTaJXhOWKuBJ87HBlugvr2TCoFhkVTW7ubtSrd28ZdEP7BF8/X+rTpzf17dPXqH8Xojl//nyqXqM6TRCTWtGijvIamOhg6Bm6HWA1I/kAFbG1ar5AFy9dlK4JFVj01WvUoFrie9MC0V2+PEBavdOnfyLdrHg/FTw8yMmpWKpMEVzfz2+0eA+1qZpnVRmMPX78OM2bN1fm0ZcrV06epwVmF2grcXNWVlZPZ7bDhw/TlatXyMenn9E/EMMw+uRmXBzt/GantHwhzip3Eu5IoYMYGiYCoLXrvHnz5OQBV4C//xTq2KGDTAdM77O//0AwXbp0iXz6+qRaXSOw6ezsLKzUMsrIv+CaVYXAxsTcoOjr1+UY9Obkryepn0/qn6MSERFBe/fuJW9v71QtaKPFBJEgRB7+eWNgwkCQcv369dSgQUNxnrY+d7MLtHOxYnKpclH80hGFDQhYRj5i+eLiUlI5g2EYS+DPv/6W4gmXATK0VCB2t2/dIk9P4+lvcAX4+frRi7VfJF9fX2lNGwMxkp9//pk8PNyphhB7FYyHngmVwgiBNEY1IdCIQ6iuzQsXLkjD8OWXX5av03L61Glpbbds2SrVZIGdkqxtrKm8m/HkBljVFTwqUMmSJalps2bKqHbkWpCQHj+mDRvWU1nXsuTVurUymDXM6YNmGMY4f/39pwwylyj5r/sQlmpg4B4qXKSw0QIVuCzGvzuePKt70rhx49MVZ3BXCOyli5fI0dGJbAwKUZBHDkHNqECljLCsHZ2cKOJihHxPu3fvoTfffDPVRGLIb78/aXlQRLxvFfjxA4MCMyxQQfxs3959FH/7NkVG5jwomBazCzR+0Y5OjjLCum9vMA0dNjTDP5Ix2AfNMPoELktkYxgrUJEBxSmT5c4870+YIF0d0dHXZRYE3CVZAT8DJeyYGDIqUIGgQljDw8Ip5HiI9IVnJ+UPzbbQ9Cwi4mK6BSp4LytXraaJkyaSQ2EHGVTUGrMLNKpyMFOhe1inLp2oYsVKyhF9g+UR/Od5ET2UQ5uKAtZ5995MQVR0NMUnxFNUZOTT1LH0qFypigz4X7jwpwz2BwcH0+Url2VvGgBfNApgzp8/L3/WhPffl+Ofzpgh/cCwUJcuXUopD1OooJFiFntxDoKKKBLBChguUWRP1KtXX14PInr0yFGZraLGtFRQ+QuBDj0dStu3b6MePVJvOpGWGtVryIwmuGySk5Np85bNZCPuzcnpSeYGLH/0R8eEApBauHDBF9SieXOqXaeOEHE3GSi8LSxpvB/csxbkmosDGRt6y3nOCPjN4T/Pi+ilHNoUpFcYxfwLhOl9IZ7o7IcsCKRfwgp+tU0b2c8cXf+MUb9+Perbt4/cg7Nt23bSN9yrZy9q3LixsCZP0ciRI8jbu41s44BMLaSrQVBfefll6XpEAQ2yQODDTZt6C+C+GDFipDSOOnXqRDOFsPfo0VMGJCtVqiQzRw4dPkTDhg9PFYwEaqDw1u1b1NenX7q+apVX275GXl5e8meiwMfD3YM6dvwf1a1bjwIDA2W6Xf/+/alECWeaIKz/1157jZo2ayq/BysBuE+QatetW3dq0KCBvGct4Ib9mYBZ3s/XVwY2Vq1amadcJaguQ5DGEnZHyS5oxIWMAXSO492t/3vAug4IWE52BW1lBoilkntBQgujpIsLFcyk8bupwB6A6l6IHTp0kEspLcktCxofIvSWRuUXKrJQwIA9BLUCnc6Km7n7GMDyGxODusfjtGlPNnNgzAcKdG7ejJMWvSXDAp0JD1NS5BLQ3qEQFcgFHzR8Xx9O/kAsnbrJ6iu4hfz9/WUeaU5BGhJ8iPb2mVdvmgJY8KtXr6ZlAQF0YP9+Sk5+QLNmzZICl1NwbzZ2dlTI3vxd+tZvWE/Hjh2VO6Jv3bqVTp8KpZUrvpITEmMa4F6B6+HsmTP0zY4d8rOClWF2ExD0Bgt0JiSLP/ztW7dlVDi9lB5TcuJEiPwKnxf+2Tp2bC99csc0aIKOcmgEU5BVY24Q1Pl+1y5q1qyZ9NcVKVqUegpr5+Svp2SgKaegAyG6qDkWeRLkMRfw3wYFBlHnTl1kqheqyjr+ryMdOHCA4vNoywA9cEf83s+eOUsjRoyghMQ79M4776SbUmdJsEBnEfSoVkFEGqlBaKgC9wMsvunTpwsrt2uW04WyCoI1xYoXfzo5OBQuQqVLl5Z5m1oAASkjfh5Q7wtl92qjGbXJDIIg6DioFcgbvfDnn1LEVJDsn5KSTJHXIpWRnFG1ShUq6vhk8oFwomLNMD8e7ofdu3fL41oRGRUlq+hKlS6ljJDsG2FY1cZoj5p6e+jwYelztnTLWYUFOhNQ6okdR5BYr7L3xyAaPvwtqlOnLh0+dIg2bNwgP+xbtmyVYpqWtDvJGHsY7i5jSIoQf8OG+uj45yisTYznBCy3US6LElZ1w9hd331HQ4cMoVq1alFQUJAcQ64pIvstWjR/JhIOv6rahD69B8QdIp+WR48e0aN/HqXKssD7sLOzfSZlKrvcTUqSIt+oUeOn0f3YuFgq6+pK+/fvl/mqY8eOldYWViZpyUohVHrFT4/Eey8kLHfDzR1wX7a2NvIYw2QHFmgjfP/99zRo0CBKEEvS4OB9UmSQdqMCPzDq9V9q0oTWrFkr++eirWN6GDbKSe+R1SwKCA42Qn0eYEXiOnsCA+nixYt0+fIl6tr1DeXokx1v0EgGKZDYew2+d4glevu2F4KUFsOGPOk9kFqV1R0v7MQqwbqAjfIqe1y9elXcS1e5+/pv587J992qdSvlqLBiPSrQjJkzycnJidatWycnqPR6QGSlECo7xU9Y/cjdPxgmm7BAGyHxbiKdEx/yNt7eMvgwUiz7jX2QPSq4U3FhKXl5tTF6XCuuR0c/zQLAV7zOSlvWtMAV8+DBfXrv3Xdp3LhxNGbMGKOFQtguKfZGrGwPib4KcEOgQ5gpMOwLHiMs0rv3koSgZd93iMkkSbxfWPuLFi2WmRNptyiDKAeKlQHEHOKcNndWKzAR3jCwrvEc24vZFbR8nyhjXligjdCjew/ZVB2P8ePHS0sxLfDXbtywkW4nxGdag58TFwe2DELVZeKdBPka2++goup5dqqAYK1fv0FagNu2bZMVWcZADwUrq3x0LTJKWsDt27U3OgHlxMWBKjHXcq4UISx5Nbvh1q1bZF+wkNEeDpmBXUHQg1fdVd3NzU058i9IvTp96pScnDLyUebExVHKxUVa6YYTT1R0VK5sOMpYPlyo8hygzBMlqqgkWrVqFVWrWpVq1KhJdnYFqXHjRspZ2oBmLNjIABVU/fr5CPH5mn78MYgWL15ssk1s4cMdO2Y0uQqruVXLVqlaSWoJKtQWL11C8+bOkS4kNNGpVKmyFFCtVyTY+v/HvUE0evQYOeGuWrVa+rt79+6tnKENmGw+++wzOvLLEZq/YL4cQ7rXmz3epG7du8nXDJNV2ILOJmh/6O39qgyu1atbj1o0bylFMzT0tCx91Rq4ID78cIrcUqhhw4YUGLhbbolvKnEGEDAUeOS3yk9NmjRRRrWnc5fO1LlTJxo6dJh0Jzk7l6DhYjLSWpzRK2LCxAly1x6UGaMoBm1uTbEbNN477qGaZzV6/fXXxWqsu2wkj3tlmOzCFjTzDChrX7FyBfn6+T2Xr5thGG1gC5pJBbp1LRPW5cABA1mcGSaXYQuakaDABjsuFyrkIDMgjAXZGIYxLyzQDMMwOoVdHAzDMDqFBZphGEansEAzDMPoFBZohmEYncICzTAMo1NYoBmGYXQKCzTDMIxOYYFmGIbRKSzQDMMwOoUFmmEYRqewQDMMw+gUFmiGYRidwgLNMAyjU1igGYZhdAnR/wE4iVlbbzbIrQAAAABJRU5ErkJggg==[/img]
Triple Integral Spherical Visualizer
Type "Triple Polar 1" to find in phone app.[u][br][color=#0000ff]https://www.geogebra.org/m/qtasfdky[/color][/u]
Question 1
Type "Example 2.21 a" to see the graph in app[br][u][color=#0000ff]https://www.geogebra.org/3d/w2qrqjac[/color][/u]
Question 1
Find the volume of the solid bounded by planes z=1-x[sup]2[/sup] and y+x=1 in the first octant.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAUwAAABCCAYAAAA8E++bAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAA2OSURBVHhe7Z3bqw7fG8DH7w/AF1dyIdyIIrZD4oJiCzfKKSRFtLnigtBOyiESJecoKWfixrm2slGObUVukLjdzn/A/s1n7Xl2a4955533fWfed82e51PrXTNrDu8zM2s986zTM/26fDxFURSlLP8LYkVRFKUMqjAVRVESogpTURQlIaowFUVREqIKU1EUJSGqMBVFURKiClNRFCUhqjAVJUccOHDAGzVqlNevXz8T37lzJ9ii1ANVmIqSI9ra2rwjR454zDdpamryzp8/H2xR6oHO9FGUnLJs2TJv27Zt3rhx44IUJWvUwlRK8v37d2/Hjh3e3Llzg5TG8uTJE1MNJXaZrOXkufBMVFnWH1WYSiSnTp3yWltbvQcPHgQpjePz58/Gmrp796736dOnINU96iEn/7FixQrvwoULRllu2LAh2KLUBarkihLGL/Am3r9/f1dzc7NZbhSdnZ0mAFm2vb3dLFfC7du3u/7777+upUuXmvVLly6Z9ZMnT5r1NEhDTu77yJEjTeBcHR0dZlnk5llwbgmNfjZFQy1MJZIRI0YES41n8ODBJtTCt2/fvFevXnlXrlwxVeXHjx97x48f98aMGRPsUTtpyPnixQvv+fPnZvnhw4fevn37vBs3bngTJkwwaffu3TMdPhJYV+oIWlMpLtu3bzeWFlkBqytMPS3McrIA22zLjWXSSoWwldfU1NRjrVVLNXKCLVc4cJ9t+A+xMhV3UAuzwND+9fPnT+/Hjx9miMrXr1+DLfWnWlmmT5/ey+IKB7YLdJbQtugroiClcmq5Z1HySdiyZUuwVzevX7/2fKVcs8WqpIz/sJQCQtsYj7+cBYM1hlWWJUllkf1oj6wErDWObWlpMRahWG6lrMNSZC0n+yMT8orlTJtmmu2sSm2owiwoKI+4qjZVRAqsHcLVxrQoJwuEZSEkhXOj9FFkwDJVallPStZycn+RSxQtipPjK1XsSnbowPWCwjhB33r09uzZE6Q0DpdkiSMvcirZoW2YBUTa8gYMGBCkNA6XZIkjL3Iq2aIKs4B8+PDBxGPHjjVxI3FJljjyIqeSLaowC8j79+9N3L9/fxM3EpdkiSMvcirZogqzgPz+/TtYajwuyRJHXuRUskUVZgF58+aNiYcOHWriRuKSLHHkRU4lWxquMGlMd937TF/j169fJnZh+qNLssSRFzmVbGmYwsQ9FV6jhwwZ4s2YMSNIVeoBLylXcEmWOPIiZ1pQNgl4X6oVKeuDBg0KUmoDA0vkw6tWPSmrMEUwOwi4y7fTK7EUcU/F1LI8Yz84CbbvSMkoElwBJxSu4JIsceRFToFPVzButFo6OztNLE4/agEHIZT1yZMnBym1wXTX27dvm+U0nackoazC7OjoCJa6YSyawPxXBvLC/v37e83bLUcanl0aDdd78uTJYM0zmYIXgcCyzFtub283saJkydu3b82Lev78+b3KarVMmzYtWKqdWbNmBUvpUYnOSYOyChMnpc3NzcGa98/AXcxslELYeUBRWL9+fbDUjf0SkOWWlpa6P9hyuGTd56Wm4bqcOBfGHRxu6zBgakFczI0ePdrEtUBzBhZ6mmNYnz592pDnkagNc+HChcFSt48+m8uXL3vr1q0L1rrhBuHVBWVKVZSYthAeaDnsar5Ub8NVXyHcJEA1ZNKkSWaZ/+TzCrxx+W/Zh7Qw4X2oylTyNT6xsskU9jVyXt7yy5cvD1IaDzKBC9a9S7LEkRc56ZCiPFbTMUVbIPme/E+54+NqKCT7msPlTQJlzobyKuWQcx46dMikT5kyxcToB2muQl7BLud28x77U25Fn6Bb+BLAnDlzgj16n9Nu1+Q40pLonkSYGeVl8At9jyMBHBAIOAUgje0Cnlz8G93LaYA4csCxgL0vjgzkvALH402GNNvRga+U/tkX7HSRzU5jmXPi8UXSbC8yOGAQ34Yss6+sJ/U2I/eBYDtKQB6uxSXEC045JxL1wCVZ4siLnDZS5pIg/j0l70p+tss6cP1SnoD9OM52YkKZ4Vj+n/1Ed9jlgPOSzvnC5UNksUGfEHgOwPGc0y5r/B9y2MeTZu+TBoldqYgStC+GmxfORKKYwhdNGoELEjhW0m0k3T63ZIDwvlHp8tAIcpN5eJLGMYIoV/u/5IFwzUmwz835BO6B/V9Jse9LuSDXlxSXCn9eFFFe5LSRclEOuTbbhZykhZUNyk2UJcqJfWyjgm3kebsMAPuFlS+IrpBzAvvZZUauw1bKkmYbX4LIjly2rkmLxMOKxPzFeSpVFExg3P2vXr3apAs3b940cbhHzM9sJsYxatZETV8rVZ3iGsBukB4+fLiJk/aMcm5fuZpl+WgYVXru1aJFi8x6JYQ/QxAXXGsbVfLFxYsXjaPicFs8hNsvP378aPI61duZM2eaDs958+YFW7ub68jzfM0yTNTXLaWHW+bpA+VnzZo1wZrnnT592jR5hY9H5qimBykPO3fu9DZv3myW0ySxwlyyZEmw5Hn379/3rl+/boROY5yWC2zdurWn/YTlSlm7dq2JyTC0v9AGxIPWgc6Ky9CGaLcFwrNnz0zZjlJyGErka8p9WMneunXrn+OkLXLq1KkmthHlJvP02Zdzi3EjfQAoZ5u2trZ/ZLbxLWGzvZSRVAuJFSY3AUHg2rVr3pkzZ0zvb1/BN/MjLbikzJ49O1jqfmtjua5atSpIqQxpvE4S7MbxJEjmnDhxookbiUuyxJEXOauBF3x4rCVWXakxk3ziF+iJD8NsqPBxlAWIUr5AzUzm6R89erSXVfj3718T22MtsW4x2EqND5XO2qxqsokVJohWp6pKsE1nQTIVX7+zkXW7x70c3Jiskaq0zBWuFixJeaGcOHHCLNvVlUrIskoumdMFv44uyRJHXuRMA3qY+V5R1JhJeqexMOVLlbysZSRLFFiIWLDSHBcF5QSLkXOhBMtZhQcPHjRx1PhQZKNmt3v37sx0R0UKc8GCBcFSt6KJqm6iRDHLeXMxDAG4aaxzjLTpcXEEQYZugK1USeetwltPsPe1FZ1YW1QpBNvcF+xjdu3aZWIsQhmOgFzIbg9BwpqT6ykF1QnBXlaUeiNKvlwNRBQWUE7tj7pxrJQBthGoWaLUKCObNm3qpVjRBxhGbKOM0rQlRhZlOKr5DiXJ/lii4bHc4uhEyjMKW/oXgPKKTMA5sH737t3b0/aKtcn2SoYIlsW3UirCV4amFyquu54eLV9h9OxLTO+X3RsmPV0S7B5I9mPdPpb/k339h2z2kx4xO0SlQTjN7omjR81X5j3bOD89bLa84WOikJ5DQlQPngvIfS93LfXAJVniyIucQLkh/0o+JJBWqryS9yljBLk+yi7HSRmw83U42L3k5Hn5bynv0hOODFFlguPZTrmNQu4952Vfzsky8krPvgwlsnvSRX+k3VNescIsIjxMHoirSrASJAPaGb1RuCRLHHmRM4+gyEVR54GKquRFhTaRR48e9Ykeb6mqueA53CVZ4siLnHmDavq5c+dyNa1aFWYCaOQu1cuXN+oxDjYpLskSR17kzAO0bdJRhLL0q8u9nNXkAVWYBSUNpwpp4ZIsceRFTpdhkDo92HTgHDt2LJOxklmiCrOguJRR81Jo8la4XYSe8q6uLlNry+P9VIVZMJjeJmNPG41LssSRFzmV7FGFWTCYaubKm90lWeLIi5xK9qjCLCBZeL6uFpdkiSMvcirZogqzQMisjzQ9X1eLS7LEkRc5lfqgCrNA/Pnzx8Ti+TotmHpme+tmmlo5spIFqpGnFFnJyTRb8SAe9RUAxU1UYRYIvoPS3Nycansc4+lWrlxpBiB3Bl8a3Lhxo4njyEIWqFaeUmQhJwod3wg4sKF9FGct9mcVFIfpnvCjFAHm4IbnFDPnlmmfTP9knq6syzaySFRgGzCfl3n4gswNLkdYFv6b89hzgmUesswHzlKeUkTdM5kqaQeRMZxuB5kCyFxte44zyyK/4jZqYfZxqPIxuwILhmqq7TGG9jm/EJu0u3fveq2trT3rEOdmTlx8MW3Qtr7ipg/GyYK3bs7pKyjv6tWrJg0HtQznEefVactTijg5Ae8+/gvG/C/3CxnFj2NYLjvIFED8Rtqu4orgNq6voAqzj4MCGj9+vPl0SHgaGr40mfKJ2z7cYqGgWI9yDpsGcbKglFB0ixcv7pmKSNsjafWelhonJ6CcuXfMVvny5Yv38uXLVKvsiruowuzjMOga64ZCXqpQv3v3zsTDhg0zsRDn+d12HMt/CHSS+NXqYK03SWShN1qcTZ89e7bX97XTlqcU5eREkfMZWc4bfrlEySbB9qeKohWwigcOHBisKU7jZwylgNBmSNsZbX600dHuR0xgW1LEV6K4PqN9Dl+I1YILPc7Hee12vqSkLU8YaWuVdk3+j/+oBO45bbVcK+eLaidV3EQVZkERR8vSESGdI9UoFwo7CoDjUR6VKNwoOBdKqdrzpC2PTVTHk9zDSuBlwLHIWc2LQWkM/fjxH5yiOAHVXarXfAqhr7jUU/oO2oapOAGdPihLxkwePnxYlaXiJGphKk5Apwi90ww4r/RLmIpSL1RhKoqiJESr5IqiKAlRhakoipIQVZiKoigJUYWpKIqSEFWYiqIoCVGFqSiKkgjP+z/Dq6Wf7evSMwAAAABJRU5ErkJggg==[/img]
Quiz 2020
Double Integration
Given a solid bounded by planes [math]z=2[/math], [math]y=x^2[/math], [math]y=3[/math] and [math]x=0[/math]. Find the volume of the solid by using double integral.[br][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAPwAAABRCAYAAAD2KctXAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAAvSSURBVHhe7Z1Zjw3PG8fL/wXgN1yJiOBGSAhjieWChLHdCDEiIhKCQdxIiMGFWEcsiQuGkIjELuFmrAmJ7cKWEcQF4xWM2F6Af39q+hml9Vn6zDlzak49n6RS1XW6q6u761t71en3O8IoihIE/4ttRVECQAWvKAGhgleUgFDBK0pAqOAVJSBU8IoSECp4RQkIFbyiBIQKXlECQgWvKAGhgleUgFDBK0pAqOAVJSBU8IoSECp4RQkIFbyiBIQKXlECQgWvKAGhgldK5vTp06Zfv345jeIfKnilZG7evGnYEjGXUfxDBa+UzMCBA2OX0ldQwSslcfv2bTNr1qxu97x587qr8hs3bjRfv361v5Wb3rxXLaKCV0ri2bNnZs6cOdZ94sQJM3v2bFuNb29vN6dOnTIPHjywv5Wb3rxXLaL70islQSl79+7d+OhvKHnb2trMggULYp/K0Zv3qgW0hFfyQnX58OHD5sqVK7GPMV++fDETJ06Mj/6AP1Xs5ubmiguwN+9VS6jgFcvOnTtNXV2dLTFdcUt1edeuXdaGFy9emOnTp8dHXZApjBw50ty/f98MGDCgx+3qXPGBct8rKKjSK2HT1NRkDdTX1/9uaWmxbpdIYL8vX75s3Y2NjdYWorZ07Opyc25ra2vsk5188Sn3vUJDBR84iIZ8v7OzM/ZJB1E1NDRYd1Lw+IsoOzo6eiTCQvEp571CRAUfOJSkIuR8IMD//vvPii0psLa2NlsSI1TOIcxCGUguCsWnnPcKERV84FBCNjc3x0f54TyE5lary02W+CjZ0U67gKGzK6oW246vYlizZo3tLBs3blzsU16yxkfJjgo+YD5+/GjtsWPHWrsQI0aMMJ8/f46Pyk/W+CjZUcEHzIcPH6zdv39/a1cb3+JTi6jgA+bHjx+xyw98i08tooIPmDdv3lh7yJAh1q42vsWnFvFK8HTaPH36ND5SKs3379+tTdvcB3yLTy3iheBluePgwYPNzJkzY1+l0vg2JbWWpshKmmZ6cDmgICQ8DDsNlUomwcsNXSMwv9n1z1JSX7x40dTX18dHfRP3g4jhowvuGm6MD7x69Sp2+YFv8WHt/fLly7vn9I8aNaposbGSkDQ9efLk2KdnzJgxw64KhDFjxli7FDIJvr29PXZ1wZipsG3bNtPY2GjdLS0tNoLFMmjQIGv6Mjxva2trfGTsxyYjE3Azhg1PnjyxtuIvCHvhwoVW7J8+fTKdnZ32m27YsCFTYcba/XKTRVtJMgmeCRcNDQ3xkflnggQvh0SN+ENk/fr1sasLNxMTd1NTU48+WLnxrWblS3wYMSAtnzx5srtA2rx5s/3t+fPn1s4HzRNqLOWcU8CmIz19P5nb8IsXL45df5ZOCixjXLduXXzUBQ/OumWpFmFTTWI9cyHcajBNBnCbDrmqzLg5jyoYx9jEjSrapEmTrB/xSC67hLdv39r4SVhcy3XFIrUcPrb7jIRLjWjFihWxT3UhPuBLzcq3+FBoZZlkRKkvaYs0c+zYMes/ZcoUawNLfvkdPbhIWpM0DujGXSLMNSwHnjt3bnxGFxImaVYgXedK35nn0rNCicswLFwQWDqJH78LLGqIciTrL0srWXzBMQsf3HNZMCHhCrJyCiMrpAiT+db4uYssXH8M90v6SRis9hI/zhG4H/HCHze/yTGLNopB3gNGnhl4V8TFF6JmhY1jMQtnegPf4pOGfFvi6kLawJ/0RZoRjbjfmwVHnCfp3037cr27RgHdYORepB/OcdMU13HsXs/5ri6TlLR4RkSMGARElPxYPGTyPMAP4y6SSBM8iJ+IFeTc5P3S/GXBB0aQF4RxP55kBO718qJ55mLgg0vYhCfwDtxnKBZ5pmJMMiHmg3O5JvkOq4Vv8UkihUdSTFIouN8aeJY04UkhRhoUEK373JIpuBlAWkbhwm/oLRmPJCUNy0m14tu3b7YqRvXj6tWrZvXq1dZfYN9ySPZURg9n7devX1u7kqQtxMg1dZNnALejZfjw4dYutgeZKmmUOVg3VTCgScC7Wrp0qT3OAr290XcqyvjUN1Br7N6920TCNnv37o19uqBZy7fdsWNH7POHtEVG4vf+/Xtrw+PHj82WLVviI2POnDljm4bJ67l/rjkKaIo4pMXDpSTBL1u2LHYZc+/ePXPjxg0bGbcd0ZfZvn17d7sKd1bWrl1rbRICbbsLFy7YD6gTSvomtJNfvnxpM99kH8OtW7ds2nfFKb34U6dOtXYSxCmzCiks6euRffmkr0e2ABcePnz4T/vdhbQV1UBSMxmXkgRPoAQO169fN2fPnrW9z7VCVH1KLUGLRbZvhkuXLtmaw6pVq2KfbCTH7/OZLMNFslAlbTPKauBbfAQ6vtgKO03swOzAZA2Wbw65xMczyqzCc+fO/bVf4K9fv6ztjrWTIVCwTpgwIfb5G34nQyqmFlqS4EFyG26CYa10Evl4bHroIsduj38hyOEqjVTFJfctFcltgcSCu9SdVStVpZeFKr6sPfctPkBpS+/4o0ePusVOieyODiXhGjIJabamMWzYMCtgwiKtFfpuR44csfa0adOsnaS5udkWulAo0y9Z8IsWLYpdXUJJq66SCVDdoWorQw68DI65Rtq0PDhGkCEaoCoMDJFwDg/EywI3I+E3GUbBX8JzMwoJ1x1HlZIF9uzZY21KZJlRRTjEnWqdQGnqDqGkIfEG1630HZYsWWIOHjz4V0lN89WFdC/pjfRFE1AKQ0retGaulN4M3R04cMC6BVk4JGmUDEf6kYB06Q638Tu1R+KI1u7cuWPjkTN9RiVDyUQ3sL2D7lBBEnoaowTffS42vZf0bgrSAynG7bHkenpH8cfmXLfnXXpC08JI85PeYNe4vdv0ntIjL79xT+7nxhd/ws6H9MZicvWsVhN5N4Weo7fwLT4yBJdm3PTJt5X0KelaRqc4L+3bcw6/53pWeReES3rkfNxoh7BBRppc7cl13NdNry49EnyIkDnw4n0UcRYkcbjDQ9XEt/hUEtKOm2n0JiVX6UNl3759tk3X13vcpc3sy+4yvsWnklANZ8puNVDBZ4ROtEJDH32B3pgDkQXf4lNu6urqbDsfsUe1maoVGCr4wBk9enTs8gPf4lMO6Lyjo5p59SywqmaBoYIPHF8Wqwi+xaccUJpHzWc7ilTt2qEKPlBIfDLvwAd8i0+tooIPlI6ODq9KU9/iU6uo4AOmErux9ITejk9yf4RCk6lqARV8gMj0S1/+4aVa8WHFGrPiaF8zo+7QoUPxL7WLCj5Afv78aW13N5ZyQakpOw0x51ymOOejkvHJB7va7N+/37qZB1CtsfHeRAUfIOyN1tDQUPY2M8NPK1euNOfPn7ebPsKmTZusnY9KxadYGBtnQUutLO/Oi51vpwQF87KT6x+Y7ok/hnnYsoaBdRDAVFCSS5qRaaLM82YdgiDzvQuRjA/3JxymMMuuLzI/XXZJcu+fNEzTFYgb4TAlmnDlWOBY7pG2Q02toYIPBIRAwkY4IlAXBIcgRHwInfNd8RSCc92wZaFSGvniI3FB9CJw4FjEWQzcn/MRMuFgyzHI/H3X1Doq+EBAyCRoxIWYcoEwpJTPShbBFxMfNzzOSWYMxSI1jSyZRa2ibfhAYGJL9L1z7twiMKc9qvL+c06+nXfcDSFkTwKgM46w0igmPvTay54H7AwTZQDWDWnxEJMcXpP944YOHWrtkOmH6mO3Eij0rCPOd+/emfnz59v/92MiDBs0Jv9cIx9svDB+/Hj7l0js8EMnGOPbpfZ+0wkY1QTsPx5du3atu0e9GBgdYIMJOuPYRefo0aNm69at9je2IKtWB2HVQfBK2FB1piNL1qJTrSdpJDv2ioFrCIvr6QcopWngQli03bOGI80Jng2kWh9Cx1w+tIRXvIVSmuYC+7XVwpJkH9A2vOIdNAUQO2P4x48fV7GXES3hFe+g4422OxN49M81yosKXlECQqv0ihIQKnhFCQgVvKIEhApeUQJCBa8oAaGCV5SAUMErSkCo4BUlIFTwihIQKnhFCQZj/g9TvYq/LCzGQQAAAABJRU5ErkJggg==[/img]
[u][color=#0000ff]https://www.geogebra.org/classic/exybdkcm[/color][/u]
