Safe Exam Browser en GeoGebra
What is Safe Exam Browser?
[url=https://safeexambrowser.org/about_overview_en.html]Safe Exam Browser [/url] is een zogenaamde 'lockdown browser'. Dat is een browser, net zoals Chrome of Firefox, die bepaalde acties onmogelijk maakt. Het kan je laptop vastzetten in specifieke url's, (bijvoorbeeld een applet als [url=https://www.geogebra.org/m/x5mpb49v]https://www.geogebra.org/m/x5mpb49v[/url]) of de online versie van een programma om te gebruiken tijdens toetsen en examens. De uitleg vind je verder op deze pagina.[br]Safe Exam Browser kan je installeren op Windows, macOS en iPad tablets.[br]
Hoe werkt SEB?
Om SEB te gebruiken, moet je als leerkracht een 'configuratie' kiezen: je kiest een wachtwoord en de websites die de leerlingen mogen bezoeken. [br]Deze configuratie wordt opgeslagen in een zgn. [b][i]seb-bestandje[/i][/b], dat gecodeerd alle informatie bevat om een digitaal examen af te nemen. Om het examen te starten[br][list][*]bezorg je als leerkracht de leerlingen het seb-bestandje [/*][*]moeten de leerlingen vervolgens enkel dubbelklikken op dit bestand, zodat SEB opstart met de gewenste instellingen.[/*][/list]
taalinstelling in SEB ... en in GeoGebra
De systeemtaal in Windows bepaalt de taal van Safe Exam Browser en deze wordt ook gebruikt in de geopende websites. [br]Concreet: Heb je anderstalige leerlingen in je klas die weliswaar GeoGebra gebruiken in het Nederlands, maar waarvan de taalinstelling van hun computer niet Nederlands is, dan zal SEB en ook GeoGebra binnen SEB deze taal overnemen en zullen ze GeoGebra niet in het Nederlands kunnen gebruiken.[br]Let er dus op dat je je leerlingen vooraf verwittigt.
Hoe gebruik je GeoGebra in Safe Exam Browser
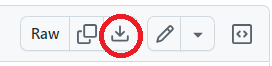
Op [url=https://github.com/geogebra/SEB]github.com/geogebra/SEB [/url] vind je reeks kant en klare links voor diverse specifieke examenmodi om te gebruiken binnen SEB.. [br]Klik je op een van deze links, dan krijg je een scherm met de volledige code van het bestand.[br]Klik nu rechtsboven op het icoon downloaden en sla het op in een map van je computer.

Via de verkenner vind je een seb-bestand dan terug met een typisch icoon.[br]Je kan meerdere bestanden opslaan en configureren en ze een herkenbare naam geven.

SEB configureren
Klik linksonder op het Windows logo en scroll tot de map Safe Exam Browser.[br]selecteer hierin de SEB configuration Tool. In dit scherm kan je de parameters van je examen vastleggen.[br]Hoe je SEB configureert om je leerlingen in een les via Klaslokaal te laten werken, lees je op de pagina[br][url=https://www.geogebra.org/m/scntsjc9#material/aqk7tvxq]GeoGebra Klaslokaal binnen Safe Exam Browser[/url].[br]Engelstalige info over configureren vind je op [url=https://safeexambrowser.org/windows/win_usermanual_en.html#configuration] SEB documentation[/url].[br][br]GeoGebra toont bovenaan de “hash” voor elk examen. [br]Gebruiken alle leerlingen dezelfde [code].seb [/code]configuratie dan [b]zullen de hashes boven in het scherm van alle leerlingen dezelfde zijn[/b] e.g. [b][code]746c0e52[/code] [/b]zodat je zeker bent dat de leerlingen de correcte [code].seb [/code]configuratie gebruiken die je selecteerde.[br]Uiteraard test je dit best uit voor het examen. Noteer ook de getoonde hash.
bestanden klaarzetten om te gebruiken in een examen met SEB
Je kan GeoGebra in SEB gebruiken als grafische rekenmachine bij een schriftelijk examen.[br]Verwijs je naar een specifiek online applet of een GeoGebraboek, dan kan je GeoGebra ook gebruiken in een digitaal examen. Je kan leerlingen vragen om constructies te maken of bv. werkbladen voorzien van vragen of Notitieblokvensters waarin leerlingen kunnen typen en zo vragen kunnen beantwoorden. [br]Bij het typen van antwoorden op een vraag in een werkblad kunnen leerlingen gebruik maken van een formule-editor. Raadpleeg hiervoor in het hulpcentrum de volgende informatie [br][list][*]'[url=https://help.geogebra.org/hc/nl-be/articles/10449584308125-Aan-de-slag-met-GeoGebra-materiaal]Aan de slag met GeoGebra materiaal[/url]'[/*][*][url=https://help.geogebra.org/hc/nl-be/articles/8828154551965-GeoGebra-Klaslokaal]GeoGebra Klaslokaal[/url][/*][*][url=https://help.geogebra.org/hc/nl-be/articles/10449195076893-Notitieblok]Notitieblok[/url][/*][/list]Op de pagina [url=https://www.geogebra.org/m/scntsjc9#material/aqk7tvxq]GeoGebra Klaslokaal binnen SEB[/url] vind je een praktische gids om een zo les klaar te zetten dat je leerlingen er kunnen aan werken in de afgeschermde browseromgeving van SEB.[br]Specifiek is het klaarzetten van bestanden zeker interessant tijdens een examen statistiek. Zinvoller dan leerlingen pakweg 50 of 100 gegevens te laten overtypen tijdens het examen zelf is een of meerdere bestanden klaarzetten in een werkblad of een boek waarin gegevens reeds ingevuld zijn in het rekenblad van Klassiek of Suite.[br][br][u]Opmerking[/u]: Je hoeft van deze bestanden geen les te maken via GeoGebra Klaslokaal. [br][list][*]Bied je in SEB rechtstreeks de url van het werkblad of GeoGebraboek aan, let er dan wel op dat je in de Geavanceerde instellingen de optie [i]Toon de menubalk[/i] uitgevinkt laat. De menubalk geeft leerlingen een ongewilde ontsnappingsroute uit SEB.[/*][*]Werk je via Klaslokaal, dan wordt de optie [i]Toon de menubalk[/i] automatisch uitgeschakeld.[/*][/list][br]
Speciale Examen URL's, ENKEL om te gebruiken binnen SEB
[u]Let op[/u]: Deze links zijn enkel bedoeld om binnen SEB te gebruiken! Als rechtstreekse link bieden ze niet dezelfde beschermde omgeving zoals de examenmodus in de online apps![br][br][url=https://www.geogebra.org/graphing?examMode=graphing]https://www.geogebra.org/graphing?examMode=graphing[/url] [br]Met deze link start je de grafische rekenmachine met de specifieke beperkingen van deze app.[br]Zie [url=https://www.geogebra.org/m/n9jjqntm]https://www.geogebra.org/m/n9jjqntm[/url] voor een overzicht van de verschillen tussen de apps.[br][br][url=https://www.geogebra.org/calculator?examMode=choose]https://www.geogebra.org/calculator?examMode=choose[/url] [br]Met deze link kan je een keuze maken om een specifieke examenmodus te kiezen. Merk op dat je op deze manier ook met de Examenmodus Vlaanderen kunt werken, terwijl dit vroeger enkel offline kon met de door leerlingen gestarte examenmodus.[br]Meer zie [url=https://www.geogebra.org/m/hyvfacwh]Examenmodus Vlaanderen[/url] voor meer specifiek informatie over de beperkingen in deze examenmodus.[br][br][left][img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAV4AAAEfCAYAAAAJL67TAAAMPGlDQ1BJQ0MgUHJvZmlsZQAASImVVwdYU8kWnltSIbQAAlJCb4KIlABSQmgBpHcbIQkQSoyBoGJHFhVcCyoWsKGrIoqdZkfsLIq9LxYUlHWxYFfepICu+8r3zvfNvf/958x/zpw7twwA6ie4YnEOqgFArihfEhPsz0hKTmGQugEC9AEZHhEuL0/MiooKB9AGz3+3dzegH7SrDjKtf/b/V9PkC/J4ACBREKfx83i5EB8EAK/iiSX5ABBlvPnUfLEMwwa0JTBBiBfKcIYCV8lwmgLvlfvExbAhbgWArMrlSjIAULsMeUYBLwNqqPVB7CTiC0UAqDMg9snNncyHOBViG+gjhlimz0z7QSfjb5ppQ5pcbsYQVsxFbuQAYZ44hzv9/yzH/7bcHOlgDCvYVDMlITGyOcO63cqeHCbDqhD3itIiIiHWgviDkC/3hxilZkpD4hX+qCEvjw1rBnQhduJzA8IgNoQ4SJQTEa7k09KFQRyI4QpBpwnzOXEQ60G8UJAXGKv02SSZHKOMhdanS9gsJX+OK5HHlcV6IM2OZyn1X2cKOEp9TK0wMy4RYirEFgXChAiI1SB2zMuODVP6jCnMZEcM+kikMbL8LSCOEYiC/RX6WEG6JChG6V+amzc4X2xTppATocT78zPjQhT1wVp5XHn+cC7YZYGIFT+oI8hLCh+cC18QEKiYO9YtEMXHKnU+iPP9YxRjcao4J0rpj5sJcoJlvBnELnkFscqxeEI+XJAKfTxdnB8Vp8gTL8zihkYp8sGXgXDABgGAAaSwpYHJIAsI23sbeuGVoicIcIEEZAABcFAygyMS5T0ieIwFheBPiAQgb2icv7xXAAog/3WIVRwdQLq8t0A+Ihs8hTgXhIEceC2VjxINRUsATyAj/Ed0Lmw8mG8ObLL+f88Pst8ZFmTClYx0MCJDfdCTGEgMIIYQg4i2uAHug3vh4fDoB5szzsQ9Bufx3Z/wlNBBeES4Tugk3J4kLJL8lOVY0An1g5S1SPuxFrgV1HTF/XFvqA6VcV3cADjgLjAOC/eFkV0hy1bmLasK4yftv83gh7uh9KM4UVDKMIofxebnkWp2aq5DKrJa/1gfRa5pQ/VmD/X8HJ/9Q/X58Bz2sye2EDuAncVOYuexI1gDYGDHsUasDTsqw0Or64l8dQ1Gi5Hnkw11hP+IN3hnZZXMc6p16nH6oujLF0yTvaMBe7J4ukSYkZnPYMEvgoDBEfEcRzCcnZxdAJB9XxSvrzfR8u8Gotv2nZv/BwDexwcGBg5/50KPA7DPHT7+Td85Gyb8dKgAcK6JJ5UUKDhcdiDAt4Q6fNL0gTEwBzZwPs7ADXgBPxAIQkEkiAPJYCLMPhOucwmYCmaCeaAElIFlYBVYBzaCLWAH2A32gwZwBJwEZ8BFcBlcB3fh6ukCL0AfeAc+IwhCQmgIHdFHTBBLxB5xRpiIDxKIhCMxSDKSimQgIkSKzETmI2VIObIO2YzUIPuQJuQkch7pQG4jD5Ee5DXyCcVQVVQbNUKt0JEoE2WhYWgcOgHNQKeghWgxugRdg1aju9B69CR6Eb2OdqIv0H4MYCqYLmaKOWBMjI1FYilYOibBZmOlWAVWjdVhzfA+X8U6sV7sI07E6TgDd4ArOASPx3n4FHw2vhhfh+/A6/FW/Cr+EO/DvxFoBEOCPcGTwCEkETIIUwklhArCNsIhwmn4LHUR3hGJRF2iNdEdPovJxCziDOJi4nriHuIJYgfxMbGfRCLpk+xJ3qRIEpeUTyohrSXtIh0nXSF1kT6QVcgmZGdyEDmFLCIXkSvIO8nHyFfIz8ifKRoUS4onJZLCp0ynLKVspTRTLlG6KJ+pmlRrqjc1jppFnUddQ62jnqbeo75RUVExU/FQiVYRqsxVWaOyV+WcykOVj6paqnaqbNXxqlLVJarbVU+o3lZ9Q6PRrGh+tBRaPm0JrYZ2ivaA9kGNruaoxlHjq81Rq1SrV7ui9lKdom6pzlKfqF6oXqF+QP2Seq8GRcNKg63B1ZitUanRpHFTo1+TrjlKM1IzV3Ox5k7N85rdWiQtK61ALb5WsdYWrVNaj+kY3ZzOpvPo8+lb6afpXdpEbWttjnaWdpn2bu127T4dLR0XnQSdaTqVOkd1OnUxXStdjm6O7lLd/bo3dD8NMxrGGiYYtmhY3bArw97rDdfz0xPolert0buu90mfoR+on62/XL9B/74BbmBnEG0w1WCDwWmD3uHaw72G84aXDt8//I4hamhnGGM4w3CLYZthv5GxUbCR2Git0SmjXmNdYz/jLOOVxseMe0zoJj4mQpOVJsdNnjN0GCxGDmMNo5XRZ2poGmIqNd1s2m762czaLN6syGyP2X1zqjnTPN18pXmLeZ+FicVYi5kWtRZ3LCmWTMtMy9WWZy3fW1lbJVotsGqw6rbWs+ZYF1rXWt+zodn42kyxqba5Zku0Zdpm2663vWyH2rnaZdpV2l2yR+3d7IX26+07RhBGeIwQjagecdNB1YHlUOBQ6/DQUdcx3LHIscHx5UiLkSkjl488O/Kbk6tTjtNWp7ujtEaFjioa1TzqtbOdM8+50vnaaNrooNFzRjeOfuVi7yJw2eByy5XuOtZ1gWuL61c3dzeJW51bj7uFe6p7lftNpjYzirmYec6D4OHvMcfjiMdHTzfPfM/9nn95OXhle+306h5jPUYwZuuYx95m3lzvzd6dPgyfVJ9NPp2+pr5c32rfR37mfny/bX7PWLasLNYu1kt/J3+J/yH/92xP9iz2iQAsIDigNKA9UCswPnBd4IMgs6CMoNqgvmDX4BnBJ0IIIWEhy0Nucow4PE4Npy/UPXRWaGuYalhs2LqwR+F24ZLw5rHo2NCxK8bei7CMEEU0RIJITuSKyPtR1lFTog5HE6Ojoiujn8aMipkZczaWHjspdmfsuzj/uKVxd+Nt4qXxLQnqCeMTahLeJwYklid2Jo1MmpV0MdkgWZjcmEJKSUjZltI/LnDcqnFd413Hl4y/McF6wrQJ5ycaTMyZeHSS+iTupAOphNTE1J2pX7iR3GpufxonrSqtj8fmrea94PvxV/J7BN6CcsGzdO/08vTuDO+MFRk9mb6ZFZm9QrZwnfBVVkjWxqz32ZHZ27MHchJz9uSSc1Nzm0RaomxR62TjydMmd4jtxSXizimeU1ZN6ZOESbblIXkT8hrzteGPfJvURvqL9GGBT0FlwYepCVMPTNOcJprWNt1u+qLpzwqDCn+bgc/gzWiZaTpz3syHs1izNs9GZqfNbpljPqd4Ttfc4Lk75lHnZc/7vcipqLzo7fzE+c3FRsVzix//EvxLbYlaiaTk5gKvBRsX4guFC9sXjV60dtG3Un7phTKnsoqyL4t5iy/8OurXNb8OLElf0r7UbemGZcRlomU3lvsu31GuWV5Y/njF2BX1KxkrS1e+XTVp1fkKl4qNq6mrpas714SvaVxrsXbZ2i/rMtddr/Sv3FNlWLWo6v16/vorG/w21G002li28dMm4aZbm4M311dbVVdsIW4p2PJ0a8LWs78xf6vZZrCtbNvX7aLtnTtidrTWuNfU7DTcubQWrZXW9uwav+vy7oDdjXUOdZv36O4p2wv2Svc+35e678b+sP0tB5gH6g5aHqw6RD9UWo/UT6/va8hs6GxMbuxoCm1qafZqPnTY8fD2I6ZHKo/qHF16jHqs+NjA8cLj/SfEJ3pPZpx83DKp5e6ppFPXWqNb20+HnT53JujMqbOss8fPeZ87ct7zfNMF5oWGi24X69tc2w797vr7oXa39vpL7pcaL3tcbu4Y03Hsiu+Vk1cDrp65xrl28XrE9Y4b8Tdu3Rx/s/MW/1b37Zzbr+4U3Pl8d+49wr3S+xr3Kx4YPqj+w/aPPZ1unUcfBjxsexT76O5j3uMXT/KefOkqfkp7WvHM5FlNt3P3kZ6gnsvPxz3veiF+8bm35E/NP6te2rw8+JffX219SX1drySvBl4vfqP/Zvtbl7ct/VH9D97lvvv8vvSD/ocdH5kfz35K/PTs89QvpC9rvtp+bf4W9u3eQO7AgJgr4cp/BTDY0PR0AF5vB4CWDAAd7s+o4xT7P7khij2rHIH/hBV7RLm5AVAH/9+je+HfzU0A9m6F2y+orz4egCgaAHEeAB09eqgN7tXk+0qZEeE+YFPs17TcNPBvTLHn/CHvn89ApuoCfj7/C8CJfDOQbT9KAAAAOGVYSWZNTQAqAAAACAABh2kABAAAAAEAAAAaAAAAAAACoAIABAAAAAEAAAFeoAMABAAAAAEAAAEfAAAAAK2hPD8AAEAASURBVHgB7F0HnJS1Eh+u0ntvB0fvvVcBkS4dQRBEqoD6RASeT1BERQVFAVGp0gWkd5SO0uHoHEfv5SgHHNfz5j97Wb5b9+Aq4JH82P2+JJPJ5J9kMplkuWSKA5lgEDAIGAQMAk8NAZenVpOpyCBgEDAIGAQEAaN4zUAwCBgEDAJPGQGjeJ8y4KY6g4BBwCBgFK8ZAwYBg4BB4CkjYBTvUwbcVGcQMAgYBIziNWPAIGAQMAg8ZQSM4n3KgJvqDAIGAYOAUbxmDBgEDAIGgaeMgFG8TxlwU51BwCBgEDCK14wBg4BBwCDwlBEwivcpA26qMwgYBAwCRvGaMWAQMAgYBJ4yAm4JWZ/1/9tJlixZQrI2vAwCBgGDQJJBIN4WL/5vM61woWz1BwjpdI0W4hEREToa7yf4OdYRb6aGgUHAIGAQSGQEkrHiivN/C6mLaus28OFDCgsNJU/P5PzxENFBo/MTuS2GvUHAIGAQ+FcgEGdXg1WhHj9+ghYuXEC//jqb/PyO08svv0IdOrSjFi1aUJYsWcQqhfK9d+8eBQUFUaZMmcjFJd7GNt26dUuUeoYMGf4Btpbv2rVrNHPmTKnvIS8MOkAeLDkhIcE0YMAAypw5s11OTWOeBgGDgEEgMRCIs+LVwuzdu5cqVqxI7h5paNIv4yljxgy0a9du6tGjBzVs+ArNmTNbFC3oly9fQUOHDqN9+3ZyWka7otPuB20ZIw7FrOPh4eF2RY08V1dXQtqIEZ9RqlSpaOTIz4RWK1stG54BAQE0aNAgKliwCL30Uh0KZYscAfzBKyQkRORAGniCt64X/ECDuF4oIjhNRcqHMqBBsOdzni3Ax22z9q004SgrSj9quchC5mEQMAi8AAjESfFqBRccHEwffjiUFW9lWrlyOWXNmlUga968OdWvX58VXV1au3YtderUSdKViqDz5/0oZcoUkXHnygfKD0HXo+NI0+943r17lyJYWVoVpX4HLYKHh83l8f3331GTJo0jFSV80bZ867ebmw0Om6K0+at1faDTCwILYS+m67MqV3sm2SrRNEh3jbT0rWmP6M2bQcAg8CIgECfFq4GB22DDhvX00Uf/sytdWJTu7u5UtWoVateuA12/fkOszO3bt9PBgwfJy6uAWL6FChWkcuXKCatz587Rjh07WClfoBQpkks6rGhPT08pu2nTZipatAjBpbBy5UoKDAykPHnyiKsBVurKlauoZMmSzDuvXVlrGbVChNJEcKbwQAP5Hjx4QFWqVKH06dMLLdqyefNmlimFpEMxQ9nv3LmTjh07LrKhHTVq1BBXBQqdOHGC23ydSpcuTVu2bGW6YyJ7zZo1eTeQkf744w/au3ef7AJq1KhOxYoVk7rMl0HAIPACIcBKJ9aBlZiUYYtXde3aDWarWrt2nWIfbhRerLgUPnfu3FFFipYQuuLFS8rzv//9SGh3794jcfDo2bOXqlKlqsQnTZos+ffv35f4kCFDVY8ePeXd1TW9yp+voEqVKr0qV66CpK1Zs1boWRHLU8t45swZyV+9erWkR/f1558bhO6bb0bbSebN+03SFi1aJGk3b95UTZo0k7ROnV5XrVq1lveGDRsp9jcLzY8//ihpDRo05KeH6ty5i8S7dHlDDR/+ibz36tVLnmizj89BKafltlduXgwCBoEkiwAsxDgFrdjYilWZM+WwK5KPPx6mFi9erHx9fUXpgjmUClup6qeffhK6U6dPq7CwMMX+VeXtXVjS/P39RQ7QDh48hNPcFFugKigoWLVo8arQ9O/fXx09ekzduHFTseWp3njjDdW379vqbkCAwiJgDVq+U6dOSVnQTZw4Uf3wwzj5QJbPP/9CFgxd7tdffxVatmgVHxjK+7hx43S2+vnnXyQNi4UObMFK2p49eyVp1qxZEh85cqTCooEwd+48SWvXrr26evWapLElLGljx34vcS2vRMyXQcAgkKQRiLOrAVt2RoZKlSpFR4/50P79+9ldsJMWLFhAn302QvYMvXv3YR/wIPL29pbteurUqSU9c6bM4qvFVn769MmUP7+3bMPDwsLZjfAg0o8bRvAhp0njQadOnaGyZcvTsGHD5JaEMOGv5MmTyydtmjSSxMrLfsilafQT8rH1KwdooIPbAjcxfvllkiZh10g7dp1s5BsZndh1kIlef70zde3aVfLR1mrVqoqboHx5m4skNCzMflgH9wcC2oDQp08fOfjDe4UK5fGgd94ZQNmy2fzgwOSVVxoRLziS58wFIhnmyyBgEEhyCMRZ8QIJrSxwZaxhw4byGTjwfcIVrk2bNtFbb71Fly9fod9+myuKNyTEdqMgNDREgITirMG+z+3bttOkSZNYeR9g/+9SyatcuWrkQRjRkSMH5QYD6oHShBJE3Wwdc9ym6KzyCIPIL33bYOjQIXK9DWU0Ldui9jYgHb7cj4d9TL8WKEBnz56iyZN/YcWfRpQr/NZYZNiSJ7aC5ebG5s3b6MKFM5E1wYDFzYgweWKR0QuBxgk8dGCLn33hHtEuFJrOPA0CBoGkh0CcLtNCoSCwf5Itu75yoIQ40nG9C9Zc9+7daerUqaJIYWkiQGHanvKQQ7L+/fpT7dq1pFyvXj2F188//8yKbYddKYI6R44cUghKDDcNoFCTJWPxbSxtDB/zrW8n4KnL6yfk0gr66JGjdi6wfpGnFebvv/9ORYoU4UPCQ9SsWTNatmwxbd26Vegjm2aX2cpTM9S4IQ7ZcctDY6JpzNMgYBBI+gjEy+INCwuln3/+iWrVqiUKCcoLikRbeDjFR4DLwBr0r9rOnj1LEyf+KCf9uH6mA6xlBCg8zUsrPyt/5HnwzQcdrHk6TT+14tVx61PXAWu2RYvmNGXKFILF2qFDB751UJQaNWrEtxkCxOru338AW7w/2Ivj1gKCh4fNmn2cIpWFwl4Sd38f3Rm2JJtXg4BBIIkjECfFqxUVtt792GLt3Pl1Sps2DeHKFBQWtu2HDh2ili1bslKuQ4UKFRIY9T3ZM2fOikILD7dZzgH8izZsvaGg4Sfu3bs38e0H+aUb3BEIrGP/EVxckvFW/wJduXJFroDBVRBdgPvj6tWr8oMJ0Og2QAZcQwviuuGTLly4mChcWO5Lliyjxo0bs7vkslz/OnjQhypVqiRXylKmTMnuiLP8g5CPpEooZgTdRq5B4vIVKXyUNnA2lLW2tB8RmzeDgEEgySPAFlqcAm+bpRwrM7lZwEBh0y9XrAoVKiLvzZo1V6f5BoMOu3btknTQ4fYDbjr06tVH0urVa6A8PNLL++DBg+XZteubCrcdQD9+/ARhw0qdfzhmq3vatOmSh3y+y2vPx4umOcG3K5D/uA/fyVVjxowRmgMHDggffEF2lKtatTrfsAiU2xqaT6NGjSVv4MAP7Lz5PrKaPXuOxPnnyXY+fLdX0vherz0NbU+VKqMaMOBde5p5MQgYBF4MBOL9n+TAcsTPbk+ePCkHTxf4RxAZ2MVQvHgx+XEALEP4NmHZhbElfOb0afkZLw6tChcuLO8+Pj50ni3XnOzHLVGiBFvPaWkjuxtSpkgpNwn4ahffQkgvP5rgbmHdZ7NY8YMHWJ34Pxjwg4ps2bLZXR2ggs3JV7r4/4/wE7+uLovytlwbL/iPL126xDckUrBMhURW0KJtp0+f4R9EXBO5IDN+BIIfScASL1q0qPizkQY/doMGDegB3264yhY4fkCh3RuQ8/jx43x7I7/c3kDt2BUgDXwK8GGeCQYBg8CLg0C8FC9g0ko1Osgel6+VW3RlHdOt9FqxWmms+db02L5rPvoZ2/JWekcejnErrXk3CBgEXgwE4q14AROUKwIsRHzEjmSLEUrG6sNEHB8rLTsN7N5Qa54QRfIEf81bp+PpjJ8135HGMU/HwVvTWuVFmm4b0nV9VnoWzC6/MOEv0Fn5WMvpspq3s3ZpPuZpEDAIJE0EEkTxWqFxZola8827QcAgYBB40RGI0z3ex4FmOct/HJnJMwgYBAwCLywCCa54X1gkTcMNAgYBg0AMETCKN4ZAGTKDgEHAIJBQCBjFm1BIGj4GAYOAQSCGCBjFG0OgDJlBwCBgEEgoBIziTSgkDR+DgEHAIBBDBIzijSFQhswgYBAwCCQUAkbxJhSSho9BwCBgEIghAkbxxhAoQ2YQMAgYBBIKAaN4EwpJw8cgYBAwCMQQAaN4YwiUITMIGAQMAgmFgFG8CYWk4WMQMAgYBGKIgFG8MQTKkBkEDAIGgYRCwCjehELS8DEIGAQMAjFEwCjeGAJlyAwCBgGDQEIhYBRvQiFp+BgEDAIGgRgiYBRvDIEyZAYBg4BBIKEQiNOfd9eV40/axCRY/9xNTOid0aCuhODjjLdjWmLXpXF7Wu1xbN+T4s9KvtjUq2nRlucJRy3X05ApPnVJWSd/tupJYyO2+ajnaWARW7meNX2C/+mfZ90gU3/sEcDkwMf6d+Jiz+XplXieJvO/DbvE7iX9NxSNsn080nFWvBhwwcHBMmGtfyodgCNP/2lzvHt6ej5eiifk4g9Ooi7P5J7kkixxvSNhYeEUGhrKf3bdM9FWavDHn3fHn3Z/1sHZ38iDbMDc3d39qYoXGhYmfzjUzS1mG7G7AQHkyn+ENHXq1E9VzsdV9jSxCwoKknkWl37CGMRCq+fp49oU1zzMfcjo4eGRqPXEVb5nWc71Ew6xEQBgQrkC0HE//EhrVq+jv//eQfv27qe/tv9NWzZvpcWLljHQLnThwgU6dPAwFStRjBRPZGd/LRhp+DBb0d/WlVLXdf36DZo4cRKVLFGcUqRIQWE8QREcacEHQZeTCH/pOhDHO8rpsqDV+RiIJ4770tx5v1G5cmVE8djyIRzo0HZbvUjHxxlPSeQv0GuZ9BP17tyxi7Zu205lypS201hl0jxRRteh5cXEhhA6rmmscVgdLkyDPF2vyO4S9S8igzfK3bhxg86cOUvp0qUjKL3Vq9fSn39spMqVK0r9j3jY+omL2NM1D13/I9mBzyOsQQc+oMO7LqexwvPH8T/Rg/v3ybuAtyx+mhayA38JaBdjsHXrNvrov5/ypHanEiWL2+UBja5HyxQejnptMuu69RO0VlkkDiaR2OAVATwggy6neV+9eo3On78g2EGJ/b5wMe3evYfKlS8rtCgLnvqJcros+hLv4KnbqPOkgMMX+OADGjxnzZxDISEhlCdPHpJFy8LbxjNClCtorXIHBQXTp598RlmzZqHs2bMJ1hj7GDeg4y+7jBBB80LWIwyizj/koD0nTpzg+RlOadKkpvsPHtCECT9RjhzZKWPGjLGet+BpDVoOpOFdYyVzgtN0XNMhrrECBggyDyLnsMbFlh6zcSBMEuArZqaFpSLdOKxiLV5tZu+UKZOmU+EiBenlhg3o3r17Mhg2bdxMV69dEysmGXesDho0PB23tzpP0+IJRXv08DE7sNoiwkBgbO2dYF29NR9ndWjemsZaLiQ0hHxP+MnABh3a6+rKlVgCOgxyayx0ec0PpLZ6Uc7VUtL2ep+Vy5UrVyXiwspQ0+jytrKP8AKhznOsy4qftZz1XSqK/NJ8EEU7wO/y5Ss07vufaNKUCUKVL58XZcmSWd5t7f9nG3TbhYi/NF/MTatMyNd4adl1WV0GNAiVKlWgTJkyyrszK07oORcTbcb0OdR/QG+qWrWKxMFb8xcG/KX5wwhA0PVKJJqvJ/HQxXSbzp49R3Nm/0Y/jBsjWQULFZB6EUH9wCJ6njZcYyKX5qXrB8+LFy9Rrty5JMmdF0wE0CGAp67XsT+wWDV4uT5lzmzrY421KyaTQ3iE4T/HgM7TWKC+aVNn0qstm4myxQJ59MhxatHCZijpeaur0OW1nI7pOo6nM1rHNMQRrG3XskmG5Qu0VlwcZbDGdT2W4vF+jbXi1TVCsKJFi+goZc2WhfJ756MCBbztaejgNLwNhEV19OgxtlZTUgm2WlOlSmkHEtasn5+fgFW8eDGxHBwbivGQM1cOVuj3ZbDd4DJFixWhnDlz2vk84NX1xAlfUfoFCxSQAYluQCfcvXuXfH1PEhQeBluRIoVl+4M8dMypU6fowvmLIjsmdZYsmewDGPl+fqfoCiunzJkzcb1FZUD7+9+ihw8DOS0LHT58mLJly8aLTW57OV3v8WMn6CHvDnLmzEEFChaQrTGwy5A+PYEHcMGkgdWWJk0ae3uQd/r0aVEqXl5eMpAh26lTp0UOWBAYZ+fPn2Mr1Z1y5copbQWeaKe3d366ffs2HT9+gt00IZSbJ2gBxgVyaXwhB2j8TvpRtuxZaO/efYQ+AK/AwEDpxwsXLtp3GaDLBAy43yHfCebtye6S4sWLUsqUKYUeU/fixYtiQWN3An7IA7+rV68y71x0+tQZ7hiiYoyllgWF83rloZQ8RhDQzixZsnA9N+ncufPc/hzSb3A5Qc70GdJxWZsLCm4hLM4nWb5bLFdGVt4FGWsoFPTfuXPn2LrLSnfu3KXr16+zlZcdM5mSs3wneVy4urnKuIQshw4dFl6FCxWizLz4AC8tz6VLl8TVBd7Z2Yq7eeMmneWdQvr0aWn//gPSnrx52foMtSkaTGzIi/Fz+9Ztxjib9AtwDwkJpYu8I8yaLasswsDMyysv5z+aP1Jx5BfkuMU80AcYBwULFaQMGdLLOAYJxjfwQhoCxjzkw5i7xsYPxgqsUOxAsTgULVqY51p6aSvwyZEjp+B07dp1yp8/n8ii+wZz68jho2JVFylSSHa76NtMmWzzBO0E/pAhRYrksgMoUOCavMPaRVuBwXnux/w8LsFfz01Y7Ch38+ZNHqO5pd+sY5Q4aDkwhjDHA9jFhPENSx9YYIxjbmIOIgQE3GMZzguWKVOmoJv+/jzmTvNu6oH0mx4bqBPWf9q0aXmBOEoenh4yXqOMg8I8DlhnaBmkggT4irWrwVonGq1B37RpiwiISRkaGirKCdbAurV/0BFu1MPAh7Ru3Z+yFalYsYJMiv37DtCnwz/nLU4E+Rw4RGvXrKfyvEWDzw4TBh2Az30GbP36P1nBHWXr7LJ07KwZc6lkqeJS55UrV+jLL76RSXDzpj/98st0KlTIm3LyZMU28L9DhsnkDefBsWD+IgoKDqLSpUvJYPl1+kya8esccnN3o+3b/qadO3dTalaANWpUExmnT59B83/7nZWbK82du4DusVIrW7aMKNtJv0yTyT5z5jyqUqWibNsgNzBBp47+ZixdvHSRFfRD+v67H7ktSuqFEl+2bCUPmOPStq1bt8vErVChnPjDMfk//t8Injx3ROH/8vM0yp0np0yGCbwdv8bKAzKEhYXSkA//R2fOnqHq1atJvT//PJnu3L5DefLmppGfjeJF76bU8d2343kieMrAsg5snwMHaRG7hjw93ekgT8qy7GLZx4pt+fLVVKduLVq4cBHN43afPnNaFOeSxcvpKuO9nd1Kt1hpr2C686xAKlYsL33+558buN3fkwfjuXHDZtqzex/VrFVdFMHXo75lWc/SlEm/Ur78XlSYB7V1QH875ntWgi6yAH791Rip46SvH929E0ATxv9C+Vgxp+FJMn3aDBkXO/7exQtsTlnUfvh+PC1ftooxSEZLlqyQCVqBxxn6Yjxjhok1/7dFlIzz4fYaO3Y8+fGCC6W0ft0GUWgHWHnC5QLltJpdaFWrVpZFY+5ctmjHTpQzBih3jIPqNaqKMkE/oo5Dh44wBhVo06bNPI7+omrVq/KidofGfjeONm/axu2MkHI32QgBxqG8s/rssy/Jx+cQK38/usHjBf2c39tLFkmNi36ePHmSx8SnokTQ/+t5Lp06dVbGHRb8wTwOoLhz57ZZwFjQx3A/NG/RVOSZO3c+j9kjPB//pIqVysvYLFjQm5VxWvpo6HBuix8rQD8ZWxMnTKZixYvIYg+jCXML/O6xQlu/fgMtX7pKFmcv3hnp8f7gQSDNnTOPx70/L7yXpb3evNDv2rmLXS97ZW76swKcPPlXkRELFHbGcFf+tX2HuEwm8bzNmCm99D/GKILmj3H85Rdf83zjRYzH3S8/TeVFJb/wwpj75uux1KjRy3Ju8s3X34oyrt/gJVnAB/5nCPmzXFDyM6bPJnc2CLHoHzjgQ5+NGCVjAHpiw5+buS98aR/rpXNnz8tis3LlGqpStRIbi6mijFWrHozTO3dsnAP7vaQsK2D16Sefq6VLl0ucVz95rlu3XrVp3VGxxSJxHuSq42tdFa/uKuhhkHrrzd6KB7vk4WvmjNlq4o8/2+Pgi8CrsGrauJVau3a9Pe+7b79X8+bNl/g3X49Rc+f8Zs/bs2ev6t/vPcULAJdZp6ZMmW7P27lzl+rO9UJGBl698nILxVad5POKqsaMHqv+894gnpsRin11akD//yhWnJLPHa569+yneNVVfn6nVKXydaTee/fu2/lrmTdu3KxavdpBseUheWxVq/HjfhSZdu3arV6u30ydYh4IbD2q1zt2U7xyi1xvduul2FcoefjasmWratKoleKVXO3ds0+9+85AyWMLUvV4q68aOuR/zMNfePft8446e/as+vuvHap9u8522cH7p4m/cDxIykJOLeu+ffvVoEH/tdMuWbJM/fD9BKFjP6LUh7YjrFq1RjVq+KrUgTiwaNOqI8sWoNhlIe24cP4CshhDpXiyqDVr1jEOAeqt7n3U5yNHKZ7Mgq/QKNsYwvvob75TGzduwqv6aOgwNfa7HxRPFomDx6APhso7MO339ruKrVWJL168VHDgySVx4AkMV61cLXGeiOqNLm+p48eOS3w/t7d50zbKN7I8+rJKxZcUL4CSzwpBdencXfn4HBRM3v/Ph/YxDIIhgz+SNuF9+/a/FCtEu5zAa8rkaciS8YyxdD9yfLCBoFq2aK+2bdsu/fzugPfV1KnT7VjMn79QffHFV1IWXxiDCBirgz/8SM34dabE8YWxW7VSPYXxjPAh99+e3XvlHV+QfeD7g7lsuNq8eauqVqW+Wr/+DxkjfD7D4/p9dezoMYX3zq+/qebMnmcvywub+umnSRKf9MsU9cXnX6kQnksIB/b7qGZNWqsdf++UuHUcQd4RI76w44gx0btXf/Ury63H2oIFv8sYQGFe1NVXo0YLH3zxoidz89Kly5KmyyDCClrwlAz+4h2G8GZrXJL+99EnairPc4zPXj3elvGIjNmz5qiFXKcOvDAKLohj3Dd+paXMO8SP8fioVaMh47UFUcU7JBlXbIxJ3CqPJMTjK86uBtHytkXJrvAdosTKlWqxtYPVDSFDhgxsnWQXi/gCb60COf8SW3/wA3t4eIozfsOfW+i1ju15+5bevtqFh4fxNi2rHHjpyrC6B/E2DtuP8+wmwDYLKx9WyGDePuze6SNWT8OGL4t7AlYkVk0cAOJAAavfsaPHqWWrpnYLA9snWHkzZ9gOLXxPnKQMGTOwFbyLsKLjFgKesBzgMsnrlZMaN3mFLfRHq6FeqQsU8BaZWZGz9VOFCvAW8s3uXeXwKuBuAL38yktyiIT2pE2bhjHKzVYc8ep7nQIfPGQ5auumijXrXcBLVu9CbCVevHhFLAseoLxDKCPbLfhpceDJY0FcMC4urmytpWBL4FtesSuLFdG12xtyWwM0sNKAFQK2oVH6juOgQYCbpFq1ytIfiGMrW6VqRdnmIZ6R8cmSJRO/JZOtJG6wHOft4CF2v6RMmYq3p6G0e9cewQu+1jZtWtm2bpGHZbynARsJqDOyWnErtW7bUnYdyMSWlQe+fFAXaPW5AS9G1KpVc3ExgAYyvfZaW9q7b7+cOWCMNG/RhIpEusYCefdVrXol3hUVlHrT8g6nYuXSsv1GAtqQny1ybE3R5x/9b7BYrxgHF9n1cv7cRelHKezwxapSZIZ8B3g30a5da0oVOT7g4mjXoZVYUrCO0eG1atUU6x1svPLmlcNdB5bsbvGna1evs0+7rz0LB7N161UXNxIS0W5Gz56P+tG/2AEEcx9Wr1GR6tV7SfqdDRKms9EKjixHdd7h6YD5iu07XFTYZb7R9XVxhyG/VOmS7BYrRqyINbm041EEb1F5V6pUUepFTg7GwM/vtMxbNjzEVcJGCoXwXHZhF8y5sxdlhwzXnE1+F3ERwfVUtmxpnuMbpa3BTL9vzyFiZUkVKpRnbPqIFb982Wr6duxXdrddax5vwM+Hrdub7IbCuZN2x8AFUrlqBdl5QTa4+kqWLsouLZsLFW6T3Ox2g686oUP8FK+DNI+63ZaBQZiS/bk64LQTnY7Jhqc7b0cBCgLimTNnpl59utsHtVZiGBxQIjoOenQ8Tu5x2gyfGVudorTgs0nFPsWPhg0UHxQG0ORJ2KrnohLsb4Q/cg/fwECnQnHDrYEAHxV8gh7uHjIYEIdMAB0n14GscF3d3KhV6xbiLhA/Km913JneGiAj5MX2b9RXI0VpH2FFPX3abFaglalf/77i1tCHISgLWVAfykZEhIsPHK4NBEwo8QmzwsPWDH66smVLisvmEh+uVOKbB1Dkp0+f4cl5TbaeaAfq/27s18SWCR3mbTDcIq+8Up86vf6abJ8h46Nge0f/SHikC6EbODxKiGC82RYTbKCggH+4KHDFT3Y9sXLF9hQLW0TEdfEH58+fT9qH7Rp8sxJQ5SO2tjRLElw/Fj3C5W03AEAosovINrmBXwoeHwjAEXilZpxCeWIhjkMdjC174HqT8bVEPbHDeGFHQFsQkI6+hwyoa/GipbLFLV2mpBgRBdmNhXwJLAIUHuQD7miSknEJLJVsUUEHOZCP8cYWu9QBOfXBn9BEyoF3BNSNMYGyydlNhANtBN3GdOnSCh+koV7rIqbHIfLQP7YzAH1ga6NG56IOLC5YiHXA3LKVt530Az8EjEUEiVvGD7ghiLz8BH62OInfVCKRX1iIcQUwnPFiA5ndcEGy1cdiCDkGvNtbXCYghwwIaC/e4eaDYQLXXWoeSx9/Moj7FYs+yTyEXNA5GHsIKAMjCa4yGGpwTZYuU0rmgy2fj7UhC7cLZfEEhnBJIkA+abNuoKQmzFeCKV4MIChCa3CMIxsHbvDpZmbHfGhIGDVp0th+kg2rDSsTLE8EDbwMKZ4oj+Lc+TxooThtB3V8Il65AiudylIOhxvsYuDOcKPp02dRjZrV2CJ6VfJ4C0YbN26VCZGPOwP+zY6dOsikAAGc8lhNcRCITvW/dYs6dGgnZfHF2xCRAx3lzjLYbiXYs+2TBYctYSxHw4YN5IODpa5delHTZk0oRXK+Ehc5iHVJTEpMfKy6167dIFizuN6FyYmyhw8dE6UJeihbdiXIoH2p3kuikHmrKHK1aNFMWCIfh0eNGr8inwsXLlKXTj3E9whrHZNEB7xj4gFLCZwFBYoABcVj0R7gIwWtnqjoE2CBp5a3Xbs2tsnJpeAb5K22KBz0y+OC8IwcQ7b3R9TA+VGd3P+iFG352MFgcXnppbr2O+PwLcP/i8lsU3qPhjomF+TV4wltdOUdQmTV9jyUhUU1fdpcWrl6oRzCoEZctUN/IUDJYBGFdaQD+wik/TjkY5eATHZND+scViMw407QReSJO+q6jUjQ8mH3B+vz1KlTcgUMZXkbz77oI1T3JdvOCJwwr3SA7xqLpK2dUEzoI1sunlaFjzp1HiiQB15YWNGnMF5wJoKxiHF57OgJatassa4qyhN46PmLcQMdoNth4+3GijFUdgHYKeKQsm3b1nYeuMoI3BF0OSwwwA/nPzjLQIBCXL58pb1PJk+aypZrQapduwZ9MuxzmjR5gtQx9rsJ1K3b63KLA+Wwa9m/zwevEmx12ICRMcZtxxhHsOHE48I6ASQn/l+Plrm48LIMHJwYQxFag3YF6DSQ48ABq1sWvkP4Ur1axP4jOVjCIc+IT7+QbQU62KoY0JnXWRlhBdIB9xbhMMegadP2VfpuzHjZRuDUk32pYunhND0rb4NxIOLre1IOPmb8OosPh65JvAIfCLGPiA9uJsrhC/uHaMrkGVIFDq6qVqsqh37so2J6X1q1cg19OmyUDCxYwtf4BoFj0HLj2bP7e3yg+Ie4CHCQiJsfuC6FFRsuC2vAASKsaAz0jp3a8kHCaLkfjXJfjRpDtevUkJNclCnNE3fb1h1sOQXwNj+zTEYcaODgAafGEnjs9On5Hm3YsFGsYRwcFStROKrlZ6OUCXaaD2pWc/shGwbjXe5PBGzTsYvQAZbendt37f2Dvrl5w1/cHLjBAFcS3Cs4UN2xYycNHvSxTGJMZmzRLUNGs7Q/YdGHhtqsFfCEVaQDlCcObhCA7fXrN0WhIt6kaWNeTLfJvVbcIsEitHbNn9Sgfj1kswXuL4ugRPgLbWB/uY6K8kRf6vEF/rdu3RHLCUokTZpUokCxiOCwdffu/YR6QAfL2seHD63WrZcFG9hhsUZo3rwpH+gtZot5idBDOZz0Pc3KoZaUvXz5qr1O0EMuWMOOAeO4fYc29M1XY3nh38r1HeSDuMn09/aD9r6B0sHBMXD/848N9Nvc36VdkBFKG4ufDki7wfhBeWFGXRE5HiltKEbcoEBb2rK7Z/rU2XxguUwWexzuwniyujU0XzyT8wK0Zs16GfPo7Js3b9msxkgiWJPYQWLeNmrckGbNmEfLlq6QOTp71lyaPfM3+y4B9cvCxkoXO83vWYnCnejLc/xHvh+8ZfM2MVSA/fZtOwluhcZNGvHBci76+edJMnaLFC0oiz90wB+My0w+SMdBGowZ8MaPcHSA4XP9qnUc2PQVrPSEDq6fcIgPU4CDjsStBZykY0uDgHQoNazWuPqBIFtUbgROU6FgMFGxsv7N22H4U1+qV0cGq171wQMfWEpu7i5Cj1UYAbwzss84f37b1Rec+u/atZsO8ilxDp78Xbt2Ed8pZIJSgaWBydumbSvm5SoTsUTJEnx3tLx0xI4du2SlbdCwnpT3zp+f0vJKi5sGJ3jF38PlMVkHvNtX2hOAbT9vG/X1Msik5cU7rj9VqFhafiyBiYIOhq8sL/vxMLmwihcsWBCkgl9ISDDly5dP/JNFixbltqWjndwe+MEqVapA7dq3sVsCmIipUqWQK2jAFu4Ohklk1Vf84GooWaqoLEAHDx5mf/pD6tK5o2y50F9WjLH9TZs2NR1l6w7XqPALQVhwuHUAPycWDFzdQcDWEHWjHvAApi6uySQOJVWG/XC4xoQfiWCAd+zUTqwUTH53D1fpQ0eLRhjz14MH9+W6WTa+YhUcEiRXoeCvRYDyh0y4dgcFibGEK4XYIYAGJ/V8eCZ+VfTD2/16iQ8dygV3s3ElD4sUAvzWKdE+vlYIWrQBCwPGI2RjeFjpBovfvWDBAnxNKQtt45sKuMpVhm+TNOQxgjODUqVKiD/dg2+E+Pr6MQZFxRLH9aQCBdjHz+0oW6600MKwSM0KvHefHlwmhyhZ9sLKFTnt7oKPPkXK5IIl5IRs6Cs80c+4UglcT/mdlh9o1G9QUyxGWPxe+fLS7Tu3eUHeLm6XBg3qiXGDq5OYm2m4f63jDcoE/Qv/NuQoXry4uKBQbyDPLZw7gB5X4CpVLi+3L+DffrlhfZl7uDqaO7ft+iTGgR5TuGJ2iW/yQKnJvOebPIUKFbRbpljY0WeoG+6fUrz9x/zAD7BgcL3dv7ecweh2o+0IqCtf/rxyXoCbIJm4bN++PWUMYjHq9mZncQOBFjs6GFp52FcN/y92Q5i/nnxdrHXrV2UMw9pG/3iy+wZjGfXA2MLOoFixomJcQQbsfvPlz2d3aWh5UE98Qpx/MhxdpVhBAZUGLlq6yAGl86301nedH93TkRYTDR2IYM2zpjvjhYGilZHOj668NV3TPu4JS0ZvNZ9U9nH5j8uz1u9IZ63fSod33V+O6TGJO5a11usMz5jwjC0N6sSIi5yfMuF1P1rl0Xz/KTMUnM6NHg/H9jjj/YhL1LGHdGv5J5W18sH7k+it+U8a5468HeNWXsjDNVGcK0CBIeAe9Hvvfkhfjhohi3h86xOm/GXl4ygDutjaR4+nffSLNs0bT2sZa7p+/2edUfk45utycX0+cnzFlUNkOQiGoFcEPB3TkK8boPMRx0RBHIMTT3wcgy6n06288a75WN0Umif463RNp/noOkGj+WgZdHk8tTKPzQTStFrp6jjqQQBfHSQtsu1aDq1AtIz/oLfwsPIEnZWHY/26Tjz1IqnTbGURsw08K19JtciupQcNyjnWC3qb7DYfoqZDurNgrUvewTOSUBCLrAdJmhfqRNAYWftR42fja1PO1vbaZJbij/jZovY4yuKjeel6dL023rZCuv2I6XxNH51cmg5lNC9rmuYVnRwACPTYBQAK6zhHOj7O+CJN12N91/RIg8ywDD94/3/U9c3XZJe6cMESPqdoJEoXsmlc8I6g68K75qXrsebrNI2PVW5HnmgX+h++c+Q50uo6wVPXqesHf2dlHGXR8mgsrHFmascK5RIiJLjFGxehrMDFpbwuEx0fx3THOMojTYOt+VmfzspY86N71+WQ/zj+zsrrsrEtZ+WlecSlfiuf2L7reuMje1zrTIy2OrYH8Zi2zbFsbNtlpX8cr8flWXnE5N3aPvhDDx48xFvxcPLOn09cNFBmVpqY8IyORsuN/CdhqmmtdFDKWFCtwZrmWMYxbi33tN6fC8X7tBpr6jEIGAQSBgEoL6vySxiuLw6XBHM1vDiQmZYaBF4sBLSFaG21UbpWNGL/bhRv7DEzJQwCLxQCRskmfHfH7x5vwstjOBoEDAIGgSSPgFG8Sb6LTQMNAgaB5w0Bo3iftx4x8hgEDAJJHgGjeJN8F5sGGgQMAs8bAkbxPm89YuQxCBgEkjwCRvEm+S42DTQIGASeNwSM4n3eesTIYxAwCCR5BIziTfJdbBpoEDAIPG8IGMX7vPWIkccgYBBI8ggYxZvku9g00CBgEHjeEDCK93nrESOPQcAgkOQRMIo3yXexaaBBwCDwvCFgFO/z1iNGHoOAQSDJI2AUb5LvYtNAg4BB4HlDwCje561HjDwGAYNAkkfAKN4k38WmgQYBg8DzhoBRvM9bjxh5DAIGgSSPgFG8Sb6LTQMNAgaB5w0Bo3iftx4x8hgEDAJJHgGjeJN8F5sGGgQMAs8bAkbxPm89YuQxCBgEkjwCRvEm+S42DTQIGASeNwSeyp93DwuLoNBQRWFhiiLCFSllgyFZMiIXl2Tk5sYfdzxdCGkmGAQMAgaBpIxAMsUhMRoIpiFBERQUFG5TuBGKlapzrQoRkAcFnDy5C3nyJzraxJDV8DQIGAQMAk8TgURRvKGhERT4IJxCQiJEgUajb//RTiwBUMJu7i6UKqUreXgaT8g/QDIJBgGDwL8egQRXvA8fhovSVbBw2Y0Ql6Bt8BQpWQGneirekLiIacoYBAwCBoE4IZCgihdW7oMHYeK3dSaNVqiOedFZxBGsvFOkcKXUaYzydcTMxA0CBoF/LwIJptEeBkavdLUbGQdprq7J7P5bKOJwPmyDgmUngz1dwwl6WNBQzKlSJ5iomr15GgQMAgaBZ4JAgli88OkG3A1z2gAoVdxWwCckJJzuBYTyM4zVLJG7myulSevBh2mufNsBNx8inFrLUNBp2OrFoRvKxc2B4VQ8k2gQMAgYBJ46AvE2I6EUH9wPlytiji4DKF0PD1e52eCz35/+3upP+7Y/oGunw1jREmX2cqUyVVNS9doZqWTpjKyE3Sk4ONyp8oULw93D3WleXFCLiIiQgzyUdXFJnFsU4VyHvjsXmzr0DiGxb3agHuCAgLogY0wCymEBdHHs8JgUttA8rXZaqozyGtcx8KzljtIIE/lXIhBvixfXxe4F/NOvC6WbnC3Z69eCaP6sczR1xG1q9GZKqlwzPWXPmZwnOdGNa8G0f08ALfnhHrUckIa6vOVFXt5pKDgo7B9uB/DDQVvKVK7xAhqTxplCwySMqeJ5kgBPo44nyfCkfGftjQA2XNAZPk/il5j5wFPLm1CyaX5WuZ2lWfOdvSeGbM7qMWlJC4F4KV6eD3T3Tqjc07UaP2LperqyYn1I48f40dHdQfT+iLxUpnwmSpnSTa6LYYLDtQAL98TROzTx2/M84YkGjyhI+Vn5QqHDx6sD6nJlnZsufdytXqtCvHbtGgUEBPDhXUrKkTMHufJKYM3X9cb2aeVx5cpVun//Hrc5JeXMmVMUmjU/Ot4hISGMTSgvNKmiI0mQ9ODgYLp8+bK0O3PmzJQ2bVrh+yQZw8LCKIjLpuJ2xUcRBgUFSX3JkyePtj2OsjjGoy0YTYa1/P379+natesyzrJnz85jIUU0paImo/0hIaFMnzxK+628o5YwMYNAVARitreMWsYewy/S8Gs0q9LFNTL4cx8GhtG8GefoxP5gGvVLEapROzv7ad3lMO22fxD58weKNwUr4nIVM9Pwr4tQ8hTJ6JcfztAt/2B2UbhEHrrZqkMd4exGDuW7wXEJYs0xEyjbL774kjDRGjduTnny5KYO7TvQsWPH7IoR/GH94IPJpJ+6XmuaptNloIju3LlDw4cPZ2Wbg5o0aUG5c+em11/vTCdPnoxah4U3eIaHs/+Fw99//02DBn3IkztE4ki3ygBaqwwgssat78LAydeu3bupatXq5O3tTSVLVqZ06dLRvHm/CR+0QXg4yAeFg3D06DHq1vVNXlTuS9wqnxUPLYcQRX5Z2zF58hSaPv1XezZcMyijy4EWsty9e5e2bt0mfacVvabRT9DqYOWBdx3wrsuvXr2Gx2MmHgNNBYNKlaoQMEHQPB3L6vZv2bKFWrZsLYsjFo+tW7fS7du37X1rLY9xh48JBgErAvHy8eJnwNbBLIxZQbqy4j28+ybN/PwOjVvpTYWLpGMFHUGXLwXSxvXXyPfoA1YkirwKpKD6DbNRPrZwc+dJRb3ezUfvtDhBO+vfoFea5uaBbHOR4okAzyLq9IzeQLIROnxjUsKNEBgYSG+91YNOnTpNhw8fZuWbQyzSGTNmUPHixTn9lExCTDA3t0fQ6MmqJyLiOk0/dZl79+5RmzbtJB/KPEuWLKww7tGkSZOocOHCdOHCRVbEuRiPyDp041hmzQuT+dChw7z4eEhLXGHqc0D9Vrw1PfLw7hhHujVoHKDEateuRVOnTqUGDRqQp6cn13dI3h88eMAYdZd6xPVikU9jEhISTL//voAmT54k7EGn69ZPXZeOazms7pwbN26Qu7u7zpJdh46gnFamDx8+FHlBj6Cx07z109o/oNPpeLdid/DgQV4QG9OKFSuoUuXKFMa7i4ULF1IVfj937hzlzZvXXtbKU7c/T5689PbbfaR/gFft2rXp/PnzlCFDBlk8Qafrjhy6onzj6xNHO0xIGgi4fsIhrk15+JCtQjbS9NzEwu7q6iJW6e/zLlC+ku7UpmNenlzJ6OKFB/Td56fowI775O4Jy1XRySMPaduft6lY6ZSUKXNyypjJk4JcA2nfzgCqUjMjb+XcxELWg5hrElFxC0LXGRPZtbJavXo1DRv2Mfn4HKD8+fOzCyAFpU+fnmrUqEEbN26WrWOlSpVESWNC7dmzh3bs2CEKIFu2bDKZIAsmPhQV8m76+wsPvU1dsmQpffPN17R37x62pvOImyFDhvRUs2YtVlZLKFu2rFSuXDmpAwp2z9699Ndff4v1lDVrVknHAnDihC9bpFVo586d5Ovry3xSiSsA9UM53L+PxSuC1q9fL8od9R844MO8/pKyHh6eogg0PloRol2vNGpKI0d+Rr169RRLFy4NWL4VK1aisWPHUvv27dk/n1zatmvXLpHB3/8W06aV7fjly1e43o3Uu3cPicMtcvToUdq+fTtdvXpV6oU8d+7cpePHjws+Wmn5+fmJ5Qrct2//SxRvzZo1RMzTp0/Ttm3bBFtY+9iVoJ1//PEHnT59VnYnGTNmFBxQ55EjRwS7W7dsfQCZgQ/wwliEpQzrNFeuXKIk9ThYunSZ4Dxs2DBx56RJk0b6ZN/e/VSsWFEZG+hfhNSpUwtPWLTgi3GAxQN9Cn6wdo8f9+U6ckq70S4ELLpY4K5cuULoV09eRHX9QmC+XmgE4uVqwH94EzUoHpS8NbwTTHs3B1LlGul5YrryljmC/lh9la5eCKGCJXGwhhP0ZJSngAclc1W0YvEVun8vlCeHK5WtkJ4Obwmhm9eD5M5vVP5wAdisPsf06OLY5mGiQPHMn7+Qxo0bLxMBylMHKIX169dSx44dJQmT7PXXu9AHH3zIyncvlS5dmrfh8yQPCuGzz0ZS2bJlad++/dT/7QFUrVpN0tbY99+PE+sW1o+1Dk9PD1bGu6h161bCB5Zx375v01vde7LCPCATf8qUqZIHBQKLslOnzrRs2XKaOXOWWMlQgghQRN26daPOnd+gFi1asD88iGbNms08yrKS3EWLFi2mAgW8WQGfEHq0HZMeAcrt9Clf3iq/KnHIiHyExo0b0cqVK0SxQWFULF+Z3n//A1Yix6lu3To0YsRnQufG1wDPnj1p3xWMHj1GMPLxOchunFGsgLKLcgUPLDJQwDr89NPPbGlPk2gEr9ravbJp0yaWuQAtXryEXS07pNyGDRsJSvXzz7/kulx50fyUzpw5I2UhS5kyZWj//v3Ur98AatSoCV26dEnysLv44IMPqHr12jR+/AR7HRqDokWLMq5Lafbs2aIYgR92F8tXLpdFGEodfb5jx04ttixm6HPgtZtdEq++2poXwPPiKlEqgmUcJQsGCqAfsYPay4tq/fr1eYHqI24ZLApaBjtj8/JiIsADIU6BFaBiX6y6cT1Y3bxh+9y4HqTu3g1Vh3xuqcoZt6nNG64ovmqmzpy+r/p02aO6d9itenTcrd7i51uv2T69Xt+tOjXbpQ4fvK34l2/qwD5/Kbt181XFtyUU34qw89f1hIdx5TEMYfwLDQRWdKx5UqlVq1bZS5486ad48qnff/9dsYJTbF1K3tix36u33+5np2OrDVpLXb9+XW3btl3eWQFIPluQqkGDlxX7jRXeM2bMpth/GKWstY7de/ZI3uTJk1XHjp0UKz2Jnz17VvheuHBB8cSW9y1bttr5fPfdWOXikkri69atk3xWsBK/edNfsfJXrGjt9M2aNVfss5U4KzfFCkPeWWlL2bt3A+y0eNFy6ES23FX//gN0VPH2XMqxj1yxm0be+XBOsXKRd1/fk0ILDDw8MqolS5Yottw5L6Xig0w7n88//0J9881oiX/66Qj19dffyHufPn3V4sW29iABNLzwSJ7GhrfzEge+6A9eRCSOOps2baY+/HCwxCdMmCD527mv0G7dNv2E3HPmzBUa8Hn55YYKfQ55EXhxVU2aNFNr1jzqR979ML2LQlm2ylWVKtWEr7+/v/A5ftyGvY+Pj8R5ERBerMRVixavKl48JY6+MMEgEC+L93FLVXgw3A7sGuB/DHOky4DfUUg7viLfw/mADjQIKCNvkXFJdPiyUTokRheNwueBvR6Q37x5k62euWJhtWjRnLfZ3/Oh3y22ZPcJtwULFrAlOYstnD0S37VrN8Hq/PLLLylfvnxiKeLGwpAhQ9hCXSyHasWLF2arKFTo8cXKmnnMEesJdUyeNIV/jfeQ+eyW7TwrfbZoZ8qBGujhf4TFVbhwMXE1IA2hbdu2XN8DsaxxCOXtXdhutWbMmIFWrVouJ+1//vmntGPFiuXCH2Vhaeng4mLzF0f2hB0P0MCaC2BLHFZos2ZNafDgwWJBsxIVnuCBPN1XeIcr5IMPBlGhQgWlCuBx585FtghfFUucKNBODwJWfty/th5EneCBMGbMaN7mFxfXwLRp02jUqNHsasgmedovrH3dcKd8+eUocQmAAHUOGvQBff31V8IPu5J33nmXqteozuMJbilb+/GE7LBuO3Z8jV0RAeKe6d27F7uabBY3rFz4nWEF85oo9ePL1mbsDGw8cKsB4ZFstqkEC7xQoSLiMsHBISz4sLBwgptL02v8JMF8vZAIxEvx8nHOP0Hjseru7koZC7oSW6h8E0HxxHCn3PmSU8CdcL6H+6jKFPz+8EEEZc/rwf8fgwcfQBD53wwhV49kfODjxoM9KntEMYci51HUzGhiemLAV9ezZy/Z1oMUg79y5Uq85VwiPlkoWJsfEgd4oaIccR3Mz+8UK2N/+vnnX/jQJY8oPu3HwwRHgK8YtJjQJUqUFN8j0lEH/MfLVywTpYAtMFwOmNCog60nKYfDPlxrghukYMGCku7lZTvggaJCSJ6cHeMcUGcIl2vevIldobDFx4prDL32WidR6KVLl6IuXd7g/zfDdutACkZ+5ciRXd7gi0WA4oMsCPDHpuMrZXC1wM+MGx8TJ/4kftZGjV4RGi0P9zKXjRA/KvyuCKG84KDNGnObgvG0ywka9B1+pYjwiBfxwrWI4AJYvnwF+6yzsuJ8m+5Zbk2AXsuJhStTJludwBABPnAE8AwODpGtPuJasdtkQQrxodpK6aO0adOwu6I0H4a2EdfOf//7kRw4BgUFs7slTZRxppU+5Me4RD+Ap+YfGmpzXQUGPmS/cWrpT9698Pjx40WoBbuuOkVpr00S8/2iIvDo6D6WCGAAivFkM1giS8OCUZQ2nQeVrJacDh0IoJp1svOkcKWXG2ejHetP0U33MM5nq4vLB9wOo3OHw+j173LzAYwHK+kIOnEsgPJXdKdMWZKLgooiFg94F7aItQUTJS+aiLaqMHG6dOksJ9BNmzYV/6Dmg+tfgwYN4UOltnzFKI0cVpUoUZwPn3rZucIqxQ2FsmXL0Jhvv5M8+GIR4AfOn9+LcBe2Q4f2VK/eSzzZWrIiKWKX9fr1G6z4e9LHH+NAh+8O58ghhzEDBvS31zF79hzGKqV81rPPGdYy7v8iwM+KgDoQcNClAw6ZRo4cKQpTLwq4qpU6dRohsS1YDDgHHKLxtpzYdUE//jjB7qdFHq6TtWrVmu9Kp2ff7kDm+Tl99NF/kSVKGU/I5+rqFnlg5c5WajHq2eNtsTjd3Ww3FIYP/0T8zTisIwq2YwCliHZUrVoVrMQaRXvgH3/jjS586OkjvlXk4QAROxIErTT1PeMiRQrTDz9MoO7du8uNDND89dd2eumlemKtYmymTm1TxLqPQYOAOLs0+P7yFbZCV9oS+RvjI3fuXOKXhZxQrlqpggjyZMhgs8BxgIyDP+GNyngwY9wgwE+NxcDar9gV3Lp1WxYktMVRJilovl4sBHggxDncvx8a1QfL/l74fPlHFer3386qsrRN7fr7pvhq4Z/dvOGq+qDfAdX+lZ2q7cs7VP/u+9Tq5RfV9atBQnP08B3VtOrf6udxJ9h/HCK+XasPGf7eAPYhxzbwRJIieI4bNw56SPF2VvGJtOJrRKpq1RqS1rDhK4onmzpy+IjEv//+B8U3F9TQoUMlzpag0j49+CT5VJ75jZc8+P0Q2NpSX331taTxNTWp47ffflPly1eUtE6dXhc6PiGXOGhRBys5id+6dUvBtwsZW7duy37GteJ/RhzyIPz444+qV6/e8o4v7XOdM2eO2rx5ixo8eIiU79evP/vcbb5ctB1tQ2BFLfmvvdZR8a0ItWnTZjVw4AeSBl4IQ4YMFZnh02aXi6pdu67k8zaffdDwd5Lie7wK8uIdPnG0Y8KEHyXOd5bVg8BAeefbA4oPzNSwYcMljjYj9O3bT/FBZaT/nRT8v3yHWcGfDZ74XLp0WXzreP/f/z7m+CXFClny+va19QEfoElc+8S7dXtTMEIdus141+NAY48+3Lhxo8g2frytH9nlAFI1atRXwhNjxOoPfhgUpNidI3nwH/OiLe/Az8/vlOIri6pOnZdUy5atuB+3qN9+my/52u9vlUcqMl8vJALx+uVaSDD/5zj8c2FZ9HlmIGAbjR8/3L4VQqOGH+dVPhkNGlaEsmZLzr4uxTceQnj1DxIrJl16T8qY0ZOtLhf5z3N+meBH+/n/cvh8fFHKkzcVWw5Rf70G3vgvInGVCG3ZAABAAElEQVRTIraBe9duaWziE/SpfLIO90DhwoXYV9pStvjw37Zq1VJcBvDzLmbf5sWLl6ggWzHdunUVKw/1Ygu5YMFCtgKP8Q2JbFKmQoUK0iZYM6gLvtZp06azNefPdRRkH20btl5zyf1h+D9hNbGSky02rCkvLy+xyGGR4ioTTsTBe9GiRWKVNmrUiE/uG4nLAVeuYKU3a9ZMYODJTGvXraM5bDHjNgX8s7DA4B4ZNepLsa51+/UT907hXlm7dj1lYldBxUoVqF279nZfLR+Iify4cYHT/ObNm0mbMmXKzO6T6lLf6506yXWrM2fOipy4UoarU9hWlyxZUmSDzxpY3759R3zScEPA4sf94ZWrVvH/9+Aityn27t0ntwHwS7/GjRuzy6Y44QZEly5d+NZIVeKDLuJDRb7p8Tpfe6sgFigs1yNHjoovGDsMpCMsW7ZMdgbVq1e39wnSoQFtdr/tdgf867gFAtdC8eLF2FXTgcqXLw9SHqO3aMaMmeKbr169KlviZfgmxxlu2+tyMwTXyLp16yZ9s2HDBlrFPtxmvJOqW7euWPDz5y8QC97mT+4omAlj82UQYATipXgxie/cDuUtGbZwj/CEgvTknwyfOH6XRrx/kgqW8qSuvfLJT4Hd+a9LaFouTmHsmrh88QEtmHOeVv8aQCOn5KeKVbKwDw3/HaSFKYTlT7oM7qy0oqY/qvnxb1rpaCr44+CffVzAgZO+g4ryCFouKDzt+9M8rHXgHYc0+o6vpsHTSudYh+bvSId4BF9dgrLSwapM2KKz+1eRb61D0zumQ+lgcYSC0Hl4ahmssul8necYxyGSG1/70ul4alpH2YTIyZeVzvpuJbW2y7EPrHlWbKIrD18teFj7yMrDsf1WPs7erWUd5bfmOStr0l4cBOKleAFTdP/5OQYZDsiOHblN4785Q5d8w6j1W/hfyNJR5qy2u7z+N4PJ93gALZvjL77h94Z5USVWuvgpsWOAMk+I/xQdciFohYB3xzShYDpHGh13nED/KB+DOnS9mqdjPCY8UQYhNrS2Es6VsrVd1neUYWdNtP8bmSOtNe74Dl7WNiOO8CQ6a74jvY7j6Yw30h2DIz/kIw0BPBzz/xEHnVBHlR1JVj7O4pHFzOMFRiDeihcKEVYvG1s8YKMiiQEI5Xv1SiBt33KdNqy6RX67QskFR3pMG8GH6blLuVHdRumodr1slNcrtShdjH9HXuCM/yAHfxAzIYIz5eqMr+OEs9KAx5OkeVx5zetxNDGpw84nBvJoWv1E3QjRKazHyaZ56OfjaGPajpjS2euE7DoSh2dCtt+x+ti2xbG8iSddBOKteAEN/iex+/f++V85Ik+7HaCY79wO5v8m8iFfc8L1Jfy3ke7s+00hPxV2ZYUawj5dZwoAPBLiv4SEPCYYBAwCBoFnjUCCKF40AooXf6YH/kLHAMWJdByi4amtWRhb2MKGsWtB0zgri8M6WLsmGAQMAgaBpIBAgileKFH8WZ9gvungTPkiX2/rHIGDlauVsTUPyhiHcWnTuTnlaaU17wYBg4BB4N+CQIIpXjQYyhWWbzC7HqBJnSnTmAIDpQtLN01ao3RjipmhMwgYBP4dCCSo4tVNhssBf3U4nK+KRWfNalrHp3Y54AZDfP/MjyNvEzcIGAQMAs8DAomieNEwKF0oYPzIAu8IzpSw1QUBF4WHpwtfG7P9VWIpZL4MAgYBg0ASQyDRFK/GCUoXf64HfzkC77BooWwRcAyXjH8MgR9EuPOtBrgWcLvBBIOAQcAgkJQRSHTFawVPrFso3shEUbz8IyxnV8is5cy7QcAgYBBISgg8VcWblIAzbTEIGAQMAnFF4NGP/uPKwZQzCBgEDAIGgVghYBRvrOAyxAYBg4BBIP4IGMUbfwwNB4OAQcAgECsEjOKNFVyG2CBgEDAIxB8Bo3jjj6HhYBAwCBgEYoWAUbyxgssQGwQMAgaB+CNgFG/8MTQcDAIGAYNArBAwijdWcBlig4BBwCAQfwSM4o0/hoaDQcAgYBCIFQJG8cYKLkNsEDAIGATij4BRvPHH0HAwCBgEDAKxQsAo3ljBZYgNAgYBg0D8EcDf+32q4R9//gd/qeKpSmAqMwgYBAwCzxaBp6J4tbK1/Ufo/1Sz1vxnC4ep3SBgEDAIJD4Cia54I/jvuru4PPJoBAYGUkhIiLTMzc2NUqdObf//eB1pE7/5pgaDgEHAIPD0EUhUxasVKZ6+vr70999/k4+PD12/fl3+4nCmTJmoZMmSVLVqVSpevDj/BQoP/gsVURV1QkICyxof60Kg+Vvrtb7r/Jg+nyfr/XmSBfgBV2e7nifhjXaY/yw/piPQ0P0bEEi0/whdT6aAgAD6/fffac6cOVS+fHmqXLky5cyZU5TftWvXaP/+/bRlyxZq3rw5derYkbJmy5aoyhedYibyv2FoOpcxPDxcxo5RxM7xMan/DgQSRfFale7EiRNpz5499O6771LFihUpefLkUZAJDQ2lw4cPE+jSpUtHAwcOpOzZsyeK8kVdmLiQwap88R4UFESenp4yqYOCgtn6dndqGUcR3kkEfOBCwedZh7CwMMLHEfNnIRdDzBg/lF2Nq6urHX/0B1xPkNGZMsVYQr9hN2TNt/bfs2iPqdMgEB8EHjlf48PFUhYTAlt5TPh58+bRgQMHaNSoUVSzZk27AgANJhSCu7s7lStXjkaMGCETcPLkyfTgwQPhoWks7OP0qvmsWrWaatWqS2fOnJFJDBkRLl68RE2bNqdbt25RcHAwVahQkc6dOyd5KIsPZNYfyeAv/O24CE6H8kBA2aFDP6Jt27ZL/LFlI/lZeTt7ByOpxyKDppNKkB+Jp35qeXbs2EEffjhEFhXQanmiK4fyOmhe8oyUVeehzVHyI2XT+dYn6kQ4duwYpUyZklauWiVxLePly5epb9+3CTsjBC2jLoe+aty4Cd27d0/yd+3aRf7+/tJ/oIEcj6S2YYE0BMmLlFWnSYb5Mgg8YwQSXPHq9hw5coQWLFgglm6BAgVsEzVyEsBygXLWEwMTCFZu3759aefOnfIBH9BZJ5XmHdfnnTt32PreSd9++50sDNoqhcLcuPFPUZzubFm99967cugn9fAlDMgKWfTHPom5PS6cDgsOAVbZli3b6P59m5JAmmNZrVA0L2u+s3epC/VYZNDv4I988NJpeGp57t9/QOvWrRe5tCzIj64c+Og+icIzsu1adrQ5Sn6kbMLY8gVeur7169dJzpTJU2Vh1diH8uL366/T7TsE0OMD/gipU6ehLl26UIoUKSRepUoVgosKQbdd35OxxyPLgof1I4XMl0HgOUAgQffDeuDjuXXrVrFy4V7QARPWGvTk0mlFixalZs2asRLcSNWqVZPJhsmeLFJZaLq4PlF9mTLlafz4cVS/fj1q2bKlsNJiQW7IWLduHUqTJo3kuSRzoUuXLhEWEg8PT/ZTl6O0adOKZQYFASVw6NAhUXZFihQhb+98PNltyg35V65cEVcKFA0s+/Tp04vSP336DOXKlVMOGi9evEg1atQQXtghABdgkS8feNkwQz1Hjx5lpf6A072oWLFioqyQj6368ePH2XK/KAsY8rSiKlmyBMt/mU6e9JX2lClThnCoiXIPHgTSwYM+dOPGTZEFB51wt+jg5+cnh6KgL1u2rOThVgp2CDlyZCc/v1Ms81UqXBjtzq+L2Z96PACDadN+pT/++IO++GKU+PWxA0LALe5KlarIbgNt8Pe/xW0vQnnz5pX81KlTSV+hjQcPHqTq1WtI+YwZM4pr6uzZc+TllVesabTp6tWr9PDhQ8qfP7/sbHQ/4iwBdQIXLOY2VKUK82UQePoI8ORIsMBKUnjxll11795drVmzRuI6/XEVaZrdu3erNm3aKN7qCzlvSR9XLEZ5msfEiT+pwYOHqLVr12LuqbNnz0r5Eyd8Jc6TVvGklXe+hSF5bDFKvHfvPsrLq4CqUaOWYiUoeZAVfFq1aqPeeKObqlu3nsRRBmHjxk0S79GjlypVsoxKly6L4m2yYiWiataqo95/f6DkDx/+idqzZ68qXryU6tbtTdWjR09JX758ufDZu3efxF95pbHq16+/vC9YsFDy2C1j5/Phh4Mlr0+fPgp48qGlxF+qV1/17z9AVa5cTRUoWERkYDeLevfd91T58hXVkCFDha4rt4F91MJ3ytSpkvbOO+9G8uwr6azEJf7aa51U585vcD+/JXHeqUi+7kdE9PvixYuVd4HCCnWOHPm5tEGI+ev06dPK27uQqlPnJdWhw2vc/u7Cb8WKlULCi5rKmDGrYldFZNtdJX/RokWKFbq88wKh2ampLDdkQhg6dKhq3bqtql27rkqRIpNid4Wka7kkYr4MAs8AAWzXEizoAc0WomrRooViC0V46/THVaRpzp8/L2XZwhRyrTQfV/ZJeZrHTz/9pPr0sSkQKJQuXbpKUfYjygSG4oXigTK9cPGiunXrtrzv3bvXXsWAAe+osWPHihLx8vJWo0ePseetX/+H0G/fvl0FBNyTd75CZ88fPHiwGjXqK8WHRarLG10l/+DBQ5L/ySefqoYNX7HTrly5UpQUEpA3fvwEe96sWbNEUSFh6dJlwod9pZKPBQvy79q1W2mFvWXrVsljP6rk/fXXXwrKCnRsRUseFhMsHsDg2LHjkod+RGArV+XN663Wr1+v7ty5K3ljxoyxK9ZPPvlEDRr0odDqL9sSrASnFi1eVVCUCKgP9epFT2P/448/6qIKCw5osIBjPGTNmoPxDBBepUqV4bbtEtqLLF+uXF7qzBnbAorEuXPn8uI6WPJHjx4tfHgHpdidZJdXMs2XQeAZIpCgrgaeLPbAyk4OzuwJMXxx48M2xkM+MSwSYzK4AO7etR3isDUk2+VevXpQwYIF/8HDjf22J06ckHS2ymTbim0q2rVmzVpxhdy+dZfat29nL1unTm3mmVfcEKdO+Uk6Kw7CAZKnZ3I+nQ+j774bR926daUg3g5PnjyFSpUqKXT16tWjTz4Zzj7x9/gwqbFs3xs0aCB5H3wwkG7evMn+6b0EflOmTOP8wuyTDpHtOw4kc+TIIbTYosOXjRsiGzZs4C13YapcqbLkYdvNFjW7N26I66BJk6bsbmlDH300RO5Tjx37LWXIkIGWL19BRYoUp3379hEraUqVKhWnp6M//9xAJUqUEF448NJuENzB5kVH+kynsZYTF9HJkydp2bKl1KFDe3EVwO2AgANILy8vwQrx1q3b4CGhfv368oSrI0+ePCzvFakLvmv2Jtj9wVwhuybQn9CvtoCxExFhi/PCScOGDWfXUV3JRJ4JBoHnAYFEOVzDTQX4QaEsYhtu880CTDCrrzG2PKKnV7wYuMlkz549Gy1evITq1GnMJ+7HpQhb3faimKQhIcES9/X1YyW0n/3W2yhfvnzUr18/OYhLniK5/aYGykLpFCpkO0iEUkQ4edKP9u61lc3Gd5THjftO6EJCQil37lxCg7K1atUktgK5fCH64Ydx/CzIftFpkg/lly9ffmKrkP3DodSwYQO5YgW/540bN0RZghCHhJA7ZcpUUg6LhHd+L14sbLc3cIsDZXCtC4vIggXzafTor2jHjp18k6MCdezYiX221wX/Eyf82Kd8jHbv3suHnbuoU6eOXG9DwmEYUQpRgFKJpV4dx1MrYCh/hM2bN9OgQYNp7tx5/IOZajR79hxRkDiQREjBWEJ2fFC2fPlK4guXTP5Cuq1/bD5tW3oyXhSiXk+EXx3tRkBbvb295R1t1zJJgvkyCDxDBBLF4oW1hYMm3M/FgQYGPGyNxx1o6AkHKxM/sMicOXOCw4IFQR+2gHnz5s1YiXanN9/swRO9Isup1yFPkRk3LRAGDOhnL4df4PHWVtp3/folVqwnKUuWLHISj4Vmy5aNfAj3JWXLllXKvv12X7tihOWMAzL8TBr3hLXSgbJglwEV4UOl/v37yQfKFgduUIjduvUgdj1QkyaNhScWjP37fVim1GIxw3ps3bq1LFbAkX2c1KdPb7F6Xd1gJdqQRz3AAFYtLOfdu/dQmzat5ccro8eMphLFS4qChNVcsWJZvoo2SOrDF7tPpGyK5CnYis5tv62APPDEVTEdoCBR171792WRWsVXyGDFQxGizVDoJUoU54XmjBw2opyv70mus4KwuH37Ni90u0VOtKdw4aLSBrTD09ND2gVC5Pn72yxoKchfGD9p09oORqHM3bj9CJDHBIPA84JAwo7GSAWLyQWFiwlnvw8baYU4azgsFEwM3M+EgqlVq5Z9Qmql4axcbNNu377Di8ERqQvKAZb1wIHvs4yneKLv4YlsuxfKtqNcecJ2vmfPXqzwmvGW+29RSlhQ/PxOUtasWWnChAmiHPmwTm5xDBz4gYiEO6n52DKG26Bu3XqyrYa1jGt1589fEAUJa/PhwyB7E9ifSsX4JgP7UeUGBR/MEftGZRHy5psS27ZtIx8+1Z8xYyYr2VY0f/48UZ7t2rVn98W3bEmPk6087kzPmjWDXQcl5O7runVrREHpirZt+0tuRkBZtm3bhr75ZjSXO0R/sWI9e/a03AaoUaM6uzV28YLzDlvr+9hVsFz609ZPyXjhORnFGkV79a4B9UAhIugrZLihgoA6EYoXL8YLa06aOXOW/f5upUoVCTgC5zZt27ELp4Pc7Lh//z4r5eNixWIs3L17j2+ljJcFDzcbcCMC1wMPHPBh181kGj58uFj+qAdYa9eScTIAEROeFwRc+WDkk4QSBnaV+PZ4guAKEqw7fCpVqiTKxrZVjFobJikUICb1zJkzRVG/9dZbYmFqyylqibjFMGlxfQrKr2zZMmJBgT+svzp16vK2Pw8/a4ucqdkXWoF/3gzrGIuAq6sLuyUWsxLaS59++glvuzuJ8i5durT4SufPX8BXyg6zomzOirauuAvgc61evTpbt6lo0aLF8us9+JXffLObKKbMmbPw1bbSbBlnkwbhmhf4/fbbfPHNwhUwdOgQyscKHNfQtmzZSstZAebJk5tGjhzJ9bsyxpn5J9iVxGKF1YsfiKRIkVJ8x7ly5WKlc5flK8fWfAWx/IB1unRp+aqWl/zfGK1atWa+m6Ucrmp9+eWX0l4snD169BDXx9KlSwmWOh+mSR7cGRkzZpI+hTsJITDwIftr81BpbgPGAK7/4Qme7du3F6sdWKMPIAOelStX4HK4GpePcShLvXr1Ft8y/MjN+Urh4MEfihWNXwLCAoflD7nKlCklCxPwAWa1a9eSe9/YBcBf3rlzZ/EdY4GETx1X71AHVyz1slgmGASeOQKJ+pNhbMvxizQoFFyC1wdAjq3G1nLhwoU88ZbTxx9/LJNaT1BH2oSOP84FYpVB+wixSCBYFwW8I1i3s45lka9/NGDNQ7o1jgUIP5F1/JkvaJAO5YMAeSALlJgOUIraN27lqfOje+Leq/Unu9aycA/AUrXWEx2f+KajXrRLW8ZWOZzxtuZrN4YzOpNmEHjeEEgUxYtG6kmBS/E//PCDbN1fffVVORWH/xYTGQoXynnFihVyEo//zwH/iY61vEQS+UvL6qwa5CFoxWONW99B48jHWb6VF951cKRFuqRBsTpYa9Z6oiun5dX8HZ/RlQMdylrrQJozeqQnVHBWn7M2PInOMT+h5DN8DAIJiUCiKV4IqScBTt75LiVt2rRJfp3lAV8fT25YcPglF/zBuEKEq0PWchJ5Sl9Wy9f6rqtHWxCiUwbR5SHdWVlndVhpHfk58tDYgg5B5+PdmYxIdxaeVE7nW3lGJ7sz/o9Lc+TjrC6Ud0YXRZ7H9M3j6jd5BoFnhUCiKl40Cv+hiv6pMCxc3OPEgQkCTsLh48StAARMPOuEkkTzZRAwCBgEkhgCia54gZfVHxodfjGhia6sSTcIGAQMAv8mBJ6K4gUgsGb1VtIRIFi5xtJ1RMXEDQIGgaSKwFNTvEkVQNMug4BBwCAQWwQS9gcUsa3d0BsEDAIGgRcQAaN4X8BON002CBgEni0CRvE+W/xN7QYBg8ALiIBRvC9gp5smGwQMAs8WAaN4ny3+pnaDgEHgBUTAKN4XsNNNkw0CBoFni4BRvM8Wf1O7QcAg8AIiYBTvC9jppskGAYPAs0XAKN5ni7+p3SBgEHgBETCK9wXsdNNkg4BB4NkiYBTvs8Xf1G4QMAi8gAgYxfsCdrppskHAIPBsETCK99nib2o3CBgEXkAEjOJ9ATvdNNkgYBB4tggYxfts8Te1GwQMAi8gAkbxvoCdbppsEDAIPFsEjOJ9tvib2g0CBoEXEAG3p91mxz//Y/7kz9PuAVOfQcAg8KwReCqKVyvb6P62mjX/WQNi6jcIGAQMAomNQKIrXse/HhwcHEyhoaHyhy/d3NwoRYoU9j906Uib2I03/A0CBgGDwLNAIFEVr1WRnjp1inbt2kU+Pj507do1UbyZMmWikiVLUpUqVahw4cIERWwtk1iAoA5tZbu4uNgV/5Pq02Xi4h6JT9knyZWQ+XGVM6aYPo6/4oaoyL4Bxuib6MLj+ERXBum6Du50Oxne4tKndgbgG/lXtKPb1VlpzbtBINH+yrBWoA8ePKClS5fSjBkzqEiRIqJkc+bMKZMKCnjfvn20e/duatOmDbVv356gjHXZhO4ePTkcJ3Ri1ZfQ8j+v/Jzh5yzNKj/6wqrsnClSZ2lWHgn5DnkfpzStsljfIQPi1rYkpFyGV9JEIFEUr5509+/fp0mTJtHGjRvpvffeE6WbKlWqKEjC9QArePz48ZQnTx6hy5IlS4IrX+vkCAwMpLt375KHh4coeghkzY8ioCUSEhJCrq6u8rEkx+g1JCSULXrXx1pxMWKUyETh4eEUHh7B2Lg/sSYrZsDm1q1b5ML4ZObFE4ubNV8zg5sJecAR1iesTSvdnTt36eHDQEqZMiWlS5dOilnzNR+MsYgIJZjqtJg8UU7LoOnd3R+11VldztJQFukIULrgGxBwj9KkSR2n8SGMzNcLg0D0e7k4QoDBiImFgbhgwQLavn07ff3111SvXj3SShc0yEfw9PSkypUr0xdffEG3b9+mqVOn8sR7aOcRRzGiFNMTB3UuWrSIKlasSlWr1qLMmTPT++8PpCtXrsjk0RMJdHi3yom0ESM+EwsdzMPCwuw0iGt6vOsAJYaABWjgwA/o6NGjEtfpEuEva1ldpzwjZQCdprGm294fyYq4DkKvI5byOknKOmnnli1b6fPPPxflBFrIauVrLa+tvK1bt1Lt2nUpR44cVKRwKd65dKD9+/fbrUDdXvRvv34DaOzYscITShe4gk9AQACNHj2GvLyKSN+kT5+efvxxoowFrdh03XhOnTqNxo0bJ0lotbXPpO0WLECk23Dq1Gnq+kY36tr1Td5ltZNPly5v0Lx58ygoKEhk0W1GGbyj/oMHD4o8QWwoTJ48hd1muyUdeVd554b+zZAhPZ07d05kgjw6WOXR745PK21EZL9baaLkR/abpkOelVanI82E5xQB7pwEDTzghB8PVPXyyy8rnpR2/jyI2YVny0ci3pGGD8KhQ4dUk8aN1aZNmyRupZWEOH5p/qtWrcJIVKtXr1E8QZSPz0HVvHkLVbduPcXK/rF1hoWFq8qVq9pls4ryJDlv3bot9f7119/WYv9413I6ZoRbMHPMc4w7yoK4Y5qzejTN77//rmrUqOXINgoP4RlJsXjxYmnb7Nmzla+vr/Lz81OsWCWN3UhCxRamPP/44w9JRx+ADoEXMHl++ukIVaBAYbVnzx7pm82bNwvtt99+J/mO7Vi3bp1asWKl5EX3pduEfP1+4MAB4bt48RK1c+dOtW3bdjVnzlxJmzZtWnSs1N69e1WfPn0V75bUf/7zH7V58xY77YIFC1XmzDmlTQ8fBtnTH410W5KWwU5geXFsnyXL/hpdeWf9qQtFV0bnm+ezQSBBD9e4CWIF4Llt2zZxLeDgDAFpsIStAdYCPshDwEFb02bNxDWBcsmTJxdLxrGclceT3q318mSlzz4bSY0avSLF8uYl+v77seTt7U1nz56jokWLiDzXr1+nkydPyjv80vA7I8A3DXkvX74sFl3BggXlUBBpN2/eJPiz8zJTxHnA05kzZyh79uzk7u7GbpQCcnjo7+9PgWzR58mdW3ji69KlS1IG/CEvDiJhOeXIkZOKFStKLswPFiEsRtAcPnyY0qZNSwUKFKDjx4/ThQsXKX36dExbjFKnTk1w31y8eFHq1rsMyKfrBZ6w7k6e9KMbN66LzMAAcru4uAoe164BA1/ZNpcoUULqg2ygEUz5efXqVWrVqhUtX76CmjVram/Pu+++y7uIq5FWaTnboSmXnTVrtnyOHDlCa9euo7ff7iv80bbhw4fRhg0bqEKFCsIHOK5cuZJ69uzLnx7SLrhAXF1hJxOVK1dOMMY7+gNuI4RDhw6ziyItQWbsprTMkslfkB+hZs2avOOx9WuNGtXpQeAD3qEtpI4dO8rhL9xd16/fIPSXl1deGQPjx48Teb/55hs6f/6C9Ad2PjinaNWqmdQH9rCqc+TILu4S1AUXzL1794WPVdYjR45SqtSpqGSJkjzWPUEqAeVPnz5F+fPnJ8gB90vevHlEdowrXrSkfrjmihQpLPMKGMJ9lpnpjzK+2GUBA+zqHDHQ9ZjnM0SAOyXBgl5dWUGoHm+9pWBhxjTosrBC2rZtq86fPy9FH7eax4Q3+GrevDUVy2bXzl3q3r179uI8YBUrTYlrS6t9+9dU82YthP7YsWOS17Nnb7YGa6oWLV5Vb77ZXfLmz58vebCaatd+yW7BwTLiblWw8mDx4R0WPSsf5ZWvoKShICxt5C1ZskT4jBr1lcS7dXtTnuPHT5B0PoCU+LBhw+W5Zs0aLrNU3t9+u788wYcnuWJlIXHUpwMs0po1a0sU7WV3QGTZfvIENghr1qyVeIsWLVWXLl2Vm2tq1bJla8WTX/LRHxrPFStWMG0yxQpd8tBObcHyxFfswrG3ExYu5GOFzJj8Ke+sLKQcLwKqUaPGqk2btmI1Ajsd0B72H0tU14sILOT//Od9Sf/qq69U7tz5VefOXVTXrt2E96effmrfScHy1GX5PEHyWalKWf01ZcoU1a5de8GuadPm6r///Ujovv76G4VdQM1adexyoJ2VK1dTfGisFi5cKHTe3oXU6693Zqv//+1dB3xUVfY+6QkhoYeSAAEpodfQVZoI0kFAwcLaEJQiCsiuruKuBVdxAZUFlaarwh9BabIgRUA6okhHpPeEGiD9/c93Jnd8zM4EsiZhSM79wbx3+7nfffPdc889b7Jf4rwgmqal/n33dZT4u++OsyIiyjK2j1hPPPGklH3llVedOLHJQ9IefLCf1bFjJ6t16zZWjx49pS76ff3vr0u+GeeUKVMkz2jywOT++3vzs9hSyvGiLPlm/BLRj1uOAFbDbAtmco+fOGF17drVgrkBwaRn1pEpA8Lt0qWLtXPXLin+R4kXjZg22IvCGjlylDyQkZHl5Yu7YMECJwmzpit5s2bNcvY9cOAzQrIglIEDB1nt2rUXckOB2bP/j8sHS9n58+db+LLAJIEAQr377tZimgBxGOKFDLjfu3eflAM5Ig7iZ3u43GPhQmBNWOIgfkNcQ4YMtVjTFBlQb+7ceVIWfUC+DRs2yniQxzZlycMHZO3bt5/E+SDTio6+Q0gGCViIUP4Y9wfTEO5/+GGdlDXyGpORIVZkTpgwUYjOzJ3rVRrI+GB7rTV06DCJmcXGtIlE1uLZNNVO+m7cuKnF9nTBI6O6cw5NnO3BFggLAXJA5j179kocJg7EDx48JHH7YoFnEnkwU6Dc+vXrM+aRLPa8sdiGKwSMMuz+KPVZo+dnspuVlORYAHhHwYtRdwvPDgLwBPYIFy5csMLDSzhNKUhD/cdZEUGYPHmK9A+zDML27Y75Z03Y4l2K5PFuUfJ4l2K1adNWMEYCiL5mzTrO5xXjM+OE6Qz3RhEAxs2atbBgBkEw3wGJ6MctRyBbTQ088Y7A20r+gvIW23FajCfCscEzBTxfUYdREX9Oz6WylmNMFRERETR27Ft8wDOI9u7dK94UnTt3lsawpcQ2EKFjR8e2GfXeeedt2ZYjHYdww4cP40OUIohS9erV2NQQLfJiC8sPN6ditPzJY+APuTejhwkAMrAGKYeOVapUFpPMiy+Olm3psu++IyZH2brCFGC2z2z35ANIh8lm+PDnqGTJkoLvSy+9TD16dJfDnvr169Ff//qymBfOnj37uwwZEqSlpYrc2ILOnPlv+uCDiVS0aFHJjW0UK9tryPYTH4o1a3YnH3A5+sNWFYdQ2MaagLGZLTtrYc57k26wQB7MRejzgw8+5LE9SLyIsCkkmZhQaPHib6l58+ZSH9viRYsWyjYdc8OEKHlM1vTmm2/IizZM7DZz1e9P1JUrCWJCwrYbAVtwH58w8Y5A3MiFeyP3e+/9U8wqKSnJIuO0adOpT58+Yr5gMqQ5c76i2NhYVOE6+MSYceXANz4+8NpwRIOCgtmc4njWkX7p0lnH/Duy+fP3w2SYi159dQxVrlxZciMjy8gV871r127i3ZSMG4kwcQ0ZMlgO/hDnMwKqU6e2uF8ysTqfD7hj1qtXF0WIz1XkCtw7duzA83ZB4r8L74jq561FIEeIFy9ChIWFiX0MwzPP680MFQ8mXI1gn8uOYL6seFBXrlzFBBYrNk3YEPGQPvLII2wbrUW8dZcvLG/v5IHGlxWLB9ya8B+kCiLBvQmIo118mVEeRI0rAu5xAm7iSEN5hIcffohtnZ9R7z692cd5gRAm0s/FnxN74PerVtMZtr2C4OFJAdstXKwQwsMdLlbA+LXXxlDLlncTmxzoiScel3zYfEGgrgGEgAAZ4uPixe0JcSwGwBq2RATW2JnYI2TsIH6UB7G5m8UKFaKFGKZMmSweK8Aa/yHbihUreUH4mGbN+lK8OXbu/IWvdWj58uWCIfoEoQ4e/KwQH2vYYnuHnR3/u3btwvbWB6hu3bri392sWdPrsOR9lNPGy9Yk5yLPgorMlnVZ5gVxe4B8CB99NIWio8vL/GGckBkBdnoE2HV/D4ZoM+aW5xvPhplbYIQ4AuTy8Qn9r76BqyP/ell5p+JMZ/OXLKpIABGDPPFmJx4p9MXdsm33CD/H37Nt/qw8H2PG/I1t/RWlfNWqNWwLE/HYEp0ySif64TUIXH/alU1iwf8Sb6IZ9ykhphu0bR5i3oKJ1mYOtG5Q7YbZpl0czHTseB+xSeC6OiCpTp3a80HKGekXWlccExNkhvYNooDLGerjoMy0h0awQERGRkp7OJQCOZsvMAh548Z1Qmqogy+FIS+Qf0pKKn0972s5CILmjIAve/369WnMa6/SpEkfsovd66x5NpFFDLLUrVOfycbxBcbh11dfzaVWrVqxW9UEket5dmkaP36CkCfag3wmHDt2VBaUkJACVKNmNdq3b79kgQAha/fuPeVQD3MHH16jGeKKND8/x6Mic5mxuJiDMGiuCBg7/mO848ePd2p1kPMvf3mJZsyYTt9+u5gXinmsdc+QOjt27OSDp8vUuXMnOTSUxIwPHGwiXLr0u7adkSVjMYtzUFCgHGCaPCx6lSrFOMdg0nF1LEBBTP6OV9WxkEJmQ8gYH+bULFSog/ZSU1OkT8SB14IF3/DcOg70QNyhoY4FGZhbloO8URYBB7U4/ERAWbMTRNwxRw7ir1AhWhYEHJSBdBHg3of+IRdIuG3bNrzg4vn4gJ+Pv/NhZH05QEN5+BCbZwx1cWBnnsesKD+oqyGHEeAvSbYFfnidbcHdp1u3bs5DMtYInHmuNyYPBykDBgzgA6jPnEXsbToTs3hj2jDuZB9//Im4ksG+Cnclhtjik3axReNAo1Onzhb7oVr80Evep5865CEKtZYtW+bsHa5PqAv7GeywuJ8/f4G0PWLESInjsA6HR8hbneFaB3lgo0QaDnVMOHDggKRNGD9B2nPYkEnctIxtkjUdKQ5bIuo/9dQAsY/CNS42trE1adIkkadVqzYW7MG7d++xzIENDnQQeDGRukyIbAfebb3wwgiJYxxws4qIiHIeJMGeGRAQxgdEc6Uu5srgiQSUhxxsSmDMfrI2b94i9k6kQdYjR45KPtyxEOx1eZGQPByymXlgTwYZD7DFAWOdOvW5nTipa54TRF5++RVr8OAhkj5q1IvW6NF/lnt84IwB/bOHg6TZZYYcyINcCKZNjB0Bh4LIh+3XBDO3sKfjcO7ll/8qZWC7RcBc4jDWhNat21qDBj0j2OK8AO3hMAwBcuLZMAEHkMiHPZ41Z7mHLR725YkT35c45hgBB3Yoyy8lybx+/vnnEse5iMkzh6Ao/+yzg8W1D/dmfLjXcOsR8HuVA09mtgSsyvzFktUZ9kM+aWW3mN/EVoaVHnl4UuyBIZBVH1d+kMT2ygcRomWhPFb77AiQDe5f0BCxNZ86dTpv8+eLpoK36+DKhjJt27YVeyZcn9jDgvh0nG1/vSWvcOFQqlWr1nXbQWjBTZs2le19rVq1RePctWun9NOyZSvps1Sp0jJGaLqwmaIfaJHQqvr27StbRmjUxYoVlVenl7Nb1Zw5c3lbeZgmT55MtWvXFpkiIkqyG1Rz0aKh4Tz22GOsJf7CNsDZtGzZd6y1dmMzxsOsGQWLSWXVqu/FVgmbMDCNioqUtuA6Bnc9vEzC5MEaXmkxfeClBV78WDuvRA3ZvgnsMS9FioSxuaO61MdcmHSMIyYmhk027cQO+eab77B9egtjWYN4QRHNcefOHazJl2fbZRfR9OQZ4DbRBrDAG32N2X7dqnUraWvatBksy+cynqZNm9A//jFW8IYc6A//EWC7hLsd5g0aYpkykWKSQR6TKWu0oTzGRoIz0kxdbOHDwsIFR2M2Mm3iCrNFeHiYmDggH+TFFTsR9jAh2NvxMlDLli15bu9gTKJEFrj51a1bB12JfXwNu1PiGYINd8CAp3m3VFLahKxIq169upRNYVkLFjT9waY7RFwT8UzWqlWT57SHuI9hbiEHcGQ/dJk77NL4sI7HHSPPB57FZs2aOzVq9AWTGtwOEcw4JaIftxSBHH1lGKYG8DoOUEAwxo7oOmI8IOxOxfbAWfTSSy8JkZkvmmvZ/zXu2p4cFvEXrRD7w5pgL4MvKLaBZltozzPlzRWLidnKudYzZbJ6ZZcq2Vp6+rLY5YFdEltKs/U2eSANyGMIBjKYPHOPbbPJt+fdjLz28ugLmEKGrLaHumaBBWnC9ODYvoeKGPZ+bkau7Cxj7zsrc+sO+xvJdfjwETFt9evX1zmXb7z5Jl28cIEPhcdeN3eYc+OjfaN2Nd/7EMgR4sUwzQMLZ/9x48YJMbCLmWglsN+CUHCQxm5SfLq9WF4Y4DeCnCe6pn52QoY2EVzJDF8SH9bAQJ6u/XqqIw3ZPlzLubZjK+rx1rUNFHSXZhpw14dJM1dT1n5112Zm5e11Xe/dtYUydjJ1reMunl3tuGv7j6a5ynYjrFzzXeOu8uCxhCLP5iN+5bomNWveiLXkp2jNmrVi54eXB85M5Dnlgvbn11U217Y17p0I5Bzx8niNFgg3LH6RgFatWiXbQmhEeHigbUFDatasGbVr107emAJMN3pQ/yiU5mE17dgfZNO/uzx3ctnThNYzyF2+SRnbY9Omu35c00zZrPRvyuJqb++6ceKbbZMHZe35rvUyi6Oua7C3hTxT32Bi4u7qmTxT1l7G5NnTcG/6Q7793pRDWmZ1PeWZtt3l2/uRe5Cgiyz2/s29kdFckW5vH23hP7R+aPvwCIF3CswY8FrBYR/yTR3pO6Nxk4aovYyJcyXn9zCjil68AIEcI14zNvvDABcY+Mri4UI6tkr4YRXYpjw9lKYdvSoCeR0B+3fFPlZP6fYyen97IZDjxAs4bmbbeTNlbi9oVVpFIOsI4HtgiNZcjf07661pDW9FIFeIF4PHQ4T/7gK0XfuWyV0ZTVMEFAFFIK8gkGvEm1cA03EoAoqAIvBHEcgeJ9k/KoXWVwQUAUUgHyGgxJuPJluHqggoAt6BgBKvd8yDSqEIKAL5CAEl3nw02TpURUAR8A4ElHi9Yx5UCkVAEchHCCjx5qPJ1qEqAoqAdyCgxOsd86BSKAKKQD5CQIk3H022DlURUAS8AwElXu+YB5VCEVAE8hECSrz5aLJ1qIqAIuAdCCjxesc8qBSKgCKQjxBQ4s1Hk61DVQQUAe9AQInXO+ZBpVAEFIF8hIASbz6abB2qIqAIeAcCSrzeMQ8qhSKgCOQjBJR489Fk61AVAUXAOxBQ4vWOeVApFAFFIB8h4J/bY73uL8nqX0DNbfi1P0VAEfACBHKFeM3fWpO/rYZBM+Hagz3fnq73ioAioAjkRQRynHhBqvY/ZJmSkkKpqamCpZ+fHwUGBjrz07msrwsp50XQdUyKgCKQvxHIUeK1/8n2w4cP09atW2n79u10+vRp+YvDxYoVoxo1alBsbCzdcccdhD9jba+TnVOTmVZt8kx/9oXCpOXk1fSf2/3m5Ji0bUVAEfCMQI79lWFDoNeuXaNFixbRjBkzKDIykho3bkxlypQRkgUB//jjj7Rjxw564IEHqEePHlS4cOEcI193MLhq5O7KaJoioAgoAtmJQI4QryHdq1ev0rRp02jBggU0bNgwatasGYWHh18n/xUus43Jd+LEiVS9enUaPHgwFS1aNNvJNy0tTfqFecM1QF4jMw7//Fjzzs0A2aDtQuPXoAgoAnkfgWz/pkODBIHgOnfuXFq6dCm988471L59eyfpIg//EUILFKAWLVrQ2LFj6ejRozR9+nRKSkpymh3+6BSAUBHWr19PgwY9SwkJCRI36SC9sWPfpm+/XUKrVq2iSR9Oknx8oIyR1VxNponbr8jDqOxp5t7UkzI8dnv/7733T1q9eo0UyUqfpi3Th7l6Ske+BkVAEbj1CGQ/8WaMaffu3fTpp5/Sc889RzVr1pRUQyrwaoCGByIwadHR0aLtLlu2jDZv3izls8PmacimVKlSNGXKv2jnzl3SttGAjx07Rn/+82gqX748nT0bRytXrpJ8fGABgQz2/0hHm/Y0cy/pnG/i9quRw9Q12i008O++W05nzpxB04KHvR7uTV3XdJR3TTPl3aWbPNTToAgoArcOgWwlXhCE8UpYu3YtNWjQQMwLGB4I1klkGeMFERgCQlKdOnXovvvuY/JbKVov8lHvjwS0gYDDu/79/0QrViyXuOkXJF8huhLVqlWT0tJSqXTp0pKPj4SEK/TLL7/QmjVraP/+/ZzvMFegTWjlu3btEk11z549lJycLCR45coVOnnypOTv3LmTNmzYQOfPn5c8Q7rQurdt+4m2bNlC5y9coAoVoikgIABdkr+/P6GNn3/+mTZu3ESXLl1y1kW7qHv58mXatGmT0zvkwIHf6Icf1hEOMBEgH+qBzBNZTtjQN27ceF1bUlA/FAFF4NYgwGSQbYFJUtpiorGefPJJa+HChTfdtqnLRGX16tXLYrOD1GWyu+k2PBVk9zXJ+uab+WIJuHDhgsSR3rt3H+v99z+Q+EcffWwNGPC03PPBnxUb21jK9+zZS64ff/yJ5GF8/fo9LGl9+jwg1zfeeFPymKglPnToMKtb1+5WgwaxVtGipawjR45I/r59+6zKlWOsWrXqWvfd14n/d7TKlq1off31N5K/f/+vVtWqNaxGjZpyegVpiwlV8p5//gXrmWcGW507d5H0c+fOWePGjZP77t16yHXOnDlSdv36DVbJklHWCy+MsCB/aGhRq0WLu6zTp89IfnbgKg3phyKgCGQZAWxjsy0Y8jxx4oTVtWtXi7U2adukZ9aRKQOS6dKli8XapBTPDoIwxHv8+HEhJ9YOpe0DBw5I3PQ15aOPrKeeGiB5kydPZlJ+wErLWEwWLVosZZEJkqxbt4HFHhtSdt269ZLHh4nWoUOH5H7q1GmSx9opl61vffHFFxJv1669BQJFXYx54cJFUn758uWS36pVG4sPJOUeHxMmTHTK9Pbbb0vZefO+tpISk6zZs/+PCbqJxdqtlGfNVvKB/6+//ppRdp7kYbEpUaK0xR4mEs8OXKUh/VAEFIEsI5Ctpgajs7MUsg0OCgqSJDDAzQa8UIH6TEo3W+WG5YxZAW5srNGKKQOVsNW/666WYoZA3NfH17nl79u3Lx8K/oMOHTzE2/gfaCF7ZrRp01ZMCu3a3UMLF35Dp06dEnv0PD5E5A0+mnCaI3r27CHxggULEu4xHmz/ly5dwjI8RcHBwWIS6NChPXtxlJL7s2fPsmzLOS9EzBvoNyysINumJ0tfKckpNHLUi9StW1cKDArkA8Fv2ZTTVMwhK1auoLi4OOlzy5atlJLxkkrbtm0lrVChQvT0008Sa8kShzkiK/MilfRDEVAEsgWBHHmBAnZKEI7zS54FUVkzI/NGWxaqZVoUJMManrTbvXs39m4YTM8++4wcavX/06Py9hwaQDnYahGOHDlKQ4YMFVttjx7dqVLlSrSd7b0oA4IcPvwFfhHkDHXs2IEqVKxAhcIdLnBmwQAGJiQlJUrfcK9DCAsLkyv6QrnWre+ShSoxMVHSQbhJScmEeLlyZQleD1iMriVeo+rVqjnr+vn5iu35yy9nsR35AoFcX311jPhJJ7L/dGxsEylrPhK5PtrRoAgoArcWgd/ZIRvlgK9upcqVCZ4NTZs2FbK6UfMgBJAab5EpIiKC8FZbdgaj9darV49KlSpJX301l/bu3UcjR45wdoMy8CGGLKNGjeIXOrozSQ+UfGjHvMUXjZi3/1StWgzNmTNb8iDzoEGDKIRd47BolC0b7WwTN9Bu2argHBObOFiGUkL4OCxDO0OGPCsvj6D8sGFDnVr4xYsXxdMCcvn64hVrxyEcdgYhIQUI2veQIUNQTcKSJUuEeOPPxXN+yHXYBwUFC9GbsnpVBBSBW4NAjpgaQDQtmjeXrTDbG2Vk0Dg9BeSB9LAVB3E057ogGgSQcXYE0w5IHVv1xx9/jL0u6lN0dLSzeXgLwL0MAVrpwYMHiW227N/7PXtEPEFr1zq8G0Bov/32m/zfyN4FgwcPlTr79+2jq1evsT/yoetMJXFx8awln3GSNvyWodXCK+Jvf/u71IWmjz7HjHmNOnToJK9X79u3n80DA2nmzJlSF7LB48GE/v0fpaFDhzJxz6GDLOfs2bO5bgfOtiiNTQ2rV6/kRcSUJjFXYIzOYM90JuqNIqAI5DQCfq9yyK5OQG7YauNapEgRcXniAy1q2LChEAfyXLe6SIOWiDBr1iz66aefiD0icuTVYaNVh4eHiZlgwIABspU36edYSyxYMJQaNWpEMTExohVPmzZDzA1DhjzD2iZs1j7Uq9f9YqaYOfNTOskLy1NPPcHb/MLi5lW1agwVK15cFg/jIhYfHycabtWqVdltrRZVqlSJJk54Xwgdfd15152SBl/i+vXrswwF2K77sWjYjRvH0uuvvy7a62m2KUdXiBZtGLjBZg0b7vTpM2je3Hm8EBzi+2mEfuLZllu6dBlq3qI5Bfj7A16xAaMPuNYhmMVIIvqhCCgCuYZAjrwybIgMP4jzyiuv0L333ku9e/d2arGuo4MWh9eK8XsOo0eP5gOvuxwEzQSePfqua4+e40Z2lMCvqMEua15zvsY2V/gp49AQWjrMBMgDgSWzTTbdShezgr0Ne0/2dNhvEYf2jOBQPn//JTf4CcMGbOzBpq7r1VHXEtKHXd2YVETR5Q8WzRlMXWeC3igCisAtQSDHiBejASFt27ZNXhmGzZbdxKhKlSpCwMjD9hrbeZzO40WF4cOHU8uWLQWIW00Srv3b4/Z7COsalwF4+LhRWXf5nn4uE2UR7JqruzQPomiyIqAI3CIEcoR4MRY7geA3GGC7Xb16NeH3eHH6DrKAvRFbZvxiGd5YAym71pWEHPiwy2eadyUtE0c+5DVx+72nvMzI0LRj+jVXU8c13zXdxE09e3l7HtJd40ZeU1evioAikPsI5BjxmqHYv/x45RUHRDhEQzq2xvipSNgqjZ3XXt60oVdFQBFQBPISAjlOvAALWq2xPXoC72bKeKqr6YqAIqAI3E4I5ArxAhBosvjvLmA7bN8SuyujaYqAIqAI5BUEco148wpgOg5FQBFQBP4oAjnyAsUfFUrrKwKKgCKQlxFQ4s3Ls6tjUwQUAa9EQInXK6dFhVIEFIG8jIASb16eXR2bIqAIeCUCSrxeOS0qlCKgCORlBJR48/Ls6tgUAUXAKxFQ4vXKaVGhFAFFIC8joMSbl2dXx6YIKAJeiYASr1dOiwqlCCgCeRkBJd68PLs6NkVAEfBKBJR4vXJaVChFQBHIywgo8ebl2dWxKQKKgFci4PhjXF4pmgqlCCgC3oSAhx8X9CYRvUYW/sHFTIMSb6bwaKYioAiAcEEkNyITRep6BAQ3JLkhYSXe67HSmCKgCNgQMKSLpKSkNP6jBu5/U9tWRW8ZIn9/XwoIdFhy7RgacJR4DRJ6VQQUgesQMISRmmrRfxYfoxXfxlMa/zUZpGtwj4DZFYQU8KduvUpR42YRbncK+kPo7vHTVEUgXyMAbjU75LmzD9PoPkepee8gSkvFX5P5PS9fg+Rm8MDNlxXdlBSL9ixIpUnrKlOjJiXkr+/Y/8qOEq8b8DRJEcjvCBht91x8Eg174hcKLsDb5wAfSknGX67O7+hkPn7eFFBwiC+di0ulKtVD6OXXa/If870eNDU1ZI6h5ioC+RqBlJQ0Jtt0Jl5fSmbSJfyDWqchUwQSE9OFbBPZLp6Whns/x04hg3/VjzdT+DRTEcjfCEC7xXkayNb3eqUtfwNzg9EDKxxEAjK7icFUU+I1SOhVEVAE3COQoeGqouseHk+pIF1PuwMlXk+oaboioAg4EFDGzfYnQW282Q6pNqgIKAJZQgDE7saM4UlbdB7ucT2p6lLXXT1Tx12ekdWUMfGcvCrx5iS62naeQsDib62x1+EewcTNQJHuIAOf67gks/L2Nuzl7Pdo38RNX/Yr2kC+vS17vrfe+/nLhpxS2f3Kn+992DiKe7hk+bp4ApgxwHYKtzZ4WaAcymdMhxQJCHRhYk5FfnqaRejPE8Gmsb+yvR3TX05clXhzAlVtM08hYAjNTmrm3uRhwObefO1NHHnuyrtLN+Xsebi3t4W4u2Cv6y7f29JAmqeOpFDSFaKIsv508mAq+TIjRVX0p7jTaXT6QBr5B/uQf6BDIU5JIkpjz4oS0X5Uoow/nTqaSgnn0qlcjL94EAi5sivXkf0plHiZSTSNR8x9pDOhForwpRKR/nT8txS6HJdOgSGOdkHgqdyurx/3W9Wfgjjd4jZyOijx5jTC2v5tjYCd8Hbu3EUbNmxk96pUKl6iGDVt2oQiI8vI+KCF+bK2duTIUdrxyw66864WFBYWJoQJFWvtmrUUHh5OderUdpLo1atXpb3GjRtTaCg7ynI4dOgwrVm9lhISrlChwuEUG9uQKleuJMSNvF+4bRCsxc6ivuyilHA5gRo0rE8RESVo06bNIlNoaKizD2nUCz9AdPGn0uj+R0vQnS0jKDjYn1JS02jjujga98IJGjm+DNVvUIwSE9MoNZXfluMxBAb4UiC/hvvzT+dp7NDj9PKHZSkyqgBNm3yUzp1NEfIML+RPg8aXo0KFMtgaY+fK27aep2/nxtNr4ytSiYhguoZ2U9Idr/Zyu2msDX/15THavuUqhRX2Ze04Z0Hj9UCDIqAIeELAaJH/WbKUxr71LpUoUYKJrh5dvXKFnn/uRdq3b39GVVAD0RIu17HTfbT9518y0vl7zyS5aOESenHkX+nEiRNO7TcxMZEmT/pE2kJhkPpLfx5DAQH+1DC2PoUEB9OoES/R+vUbpK09e/bSpzM+Z1JIZzJKZeJgzS4pkbU9Xzp//gL9c9wkApkjYMHwJsUgIgAADA9JREFUxgCxgliLPXU4lbr1K04PP3aHbP937jgvBHv/A9E07O3SjAlruxmEWLVaEYrh/3gxwT/AT0iycmwgtb4nkmrVLUZ331PUoS2zaaJAqB81bBTB5Boi5f14MSwYFki9+1agRwdGsi8yFixfIfqatYtJuTReNPHbCrKg5RJsqvF649OpMnkFAunQKnk/fPDgIfr4oxn09juvU4UK0SIbNNGCBQvS7Flf0Z//MkrKHT9+guLj4mn+/IVClo2bNOIvtL+QZHR0Obp06RJ9NedrenrgU0Ku2ECXLRfJbzkFC2GOe2cijRg1TLRcdII+SpUuRZ9w302aNGGyCKI2bVtSl66dRAb7x+HDR5icKrEcrEp6cYB5AeQbfyid7m4dQXFnk6hc+R+pEGNxkeU+fKgeNb8zgu4t9xN9UvMMrdiRSPv21uMcH4qp/jO1bxRESzYl09LFFRmzVDp6NJEaNy1OM4ucomR+aQFtp7Amu3jBUer36DHq0TaE5n6XTHt316b6DYtS5cKbKYBV4PZ9QunDmXVpyaLj9FD/I3Rvw2AqVtqPwnNB28X0KPECBQ2KQCYIbN36I7Vt10pIF5pkWhprY0yoHTt1pCZsbkDcl42TW7dsFaJs3boVLVm8VAgbZgLUucik++CDvemHH9bTihUr6d577xEGunr1Gmt8/rRn9x6qULE8NWzYQCSBRos+GjWKpXLlyrE2xvZN7sdotFgU0C6uAQEBUufatUS+5pLKlglemWWBGDGW4MI+dPZ0IjVoFEbLl1aiTevO05a1V+iVF/ZShcpBdNejwRQY5DgICwrCYuJDPdqEiP0XGnPdBsWZpC/TmpVn6dnhMdSyQzjNnXqOKlTykR0A6gQwvRUq6kf31A1gTdhfzAstWgcIwUaVDxQtt1Bhf+rQOISq1Q+ii+fx62uZSZ99eUq82YeltpSHEACpGTPDufhzVL58ORkd0kGIILygoEAqU6a0pCclJdHmzT/SI4/2E3vtnXc3pw3rN4p9FuUvX7pMESUjqN9DD9IzA4cxoTbkLXeQkCcO4+Lj46k8a8Vmu4s66Auvmho7ckBAIG3fvpPeffef0j/yL19KoCFDn2HbZ6AQs7dPAYvMOwA+yKriT9P+dVQIsfU9ZeiuVqUp8Voq7dh+nmZOOca263QqVIRt2KfhaeBYTOCVcPRACrXqHE5FigbRp1N/o+dHx1O/P1Wku9uUoA9fiCfizQBst63alqHd+4qL50NRLhsc4k9TPtgnh2rJiZb85gSaBdFevWDJ69A4VPPJJeOrEq+3P6kq3y1HACR47do1kQMkYEwQsNHGxcVRVFSUHIrt2LGbtm37iY7yAdvJE6fo4G+HqFv3LnLIBkJNSEigqlWrUM/7u9KXX8ymB/v2EfMB2vT3D2C7psM+C61VXjflOilsxz1z5gwTfBkmoHQqWzaSunbt7CReaMZFihSmkydPibkDsiGYK/o1C4hk3OIPaLtw/wou4EPxp1Pp+cf3UqNWoVSzThhVrhpGTZpHUMVKYTR66E75hS+7Ap+S5CDgxs2KMV4+1LlHJLXtUJJNPv5UqXIhuvuhYCZs3n2wrTchIYXOnrkmWi36jGKN15/TU9krQjwXuCkseCBfiwnd3k9uQJRL/J4bQ9E+FIHsQ8CheTq+6FFlo2gLa7MI0EBN2LljF7315juiaW778Se2ydajAgUKsPZ6jjXdOyiVTQM4EEOAOcDiQxyEHj27sW3yOC1bttzh+cDp0Gq3bdsu5GyIEteTJ0/S0MEjhJQRjyhZgipVuoOqVKksJF6jRnXRwI35A5ovAhYL2KdNW5LoBR/wo8Xv+1ppPvTGxGo0cFQZGvPWefpy6imqW/8XmvHJrzzGEIqpVYASLqZRQKhDaJBn/MF0qlQriKpVL0znzyWKJhweHsALXYJDc+5QhM6fTeM58qEfVp+mpi120yvDfqX+HXYwrqnU5t5SlMDaLQgX7Tlmgz+RkMtBiTeXAdfubj8EYBaABjtv7tf8VxiShdCg6X7yyXQm0a7s8pRIixf9R8wIndijoVfvntSpc0e6p11rWrF8lWiffv5+cpqO0cPN7OFH+tL0qf+my+wOlsJaK4g0KqoMzZzxGV1hjwkQJq6fffYFtbu3NYUWDJW+r7FN+Ap7LqDepcuX2ZvhvADqy+Wh/eIALyk5WfLhkgYTiDcFaPIFQn3p0O4UXox8qWOXsvTWmGJUvGQgPdK9INWpV1hcueLOJFMg23LTUhzSA48N7H52Z+si7GYXSP+a8CtVjdlOD7XaQb0q72AiTmJtuYSYFqDFwq0MB3G1mwZTQAjRieNXGEM/0XiRj+Ag4FvAuty3mhpkCvRDEfhvBKAxwgxQuHBhevmVF+mD9yfTunUb+bArijXZfexpEEutW7eSw7KKd0QTNGOE5OQUtrkGUMMG9Zms54sZIjgo2KnxQjutVi2GHn70AVq88D9MzA6n0eeGD6GpU6fTyBF/oZiYKlIvKiqS+jzQS9oNZK1569afafx7E4WsoUXDb7h//4fYBFGWQMqT//WxaNfw8YVtun2HdnKQh3F4g/aLoVq8aSgW6Uvvv/srDRtVhUa+XIPO8EFbgQJ+TI4B9M1Xh+m3PUlUKop9ey/zyw34qS8my8JMlSDX06eu0qbvr9Cg/qFsJ/elnZsS2U83nt3LylCDZmH8Vls6Y0p0/nA6JTdgO/ipdDYVpVB0xTCqUjeITp9IFq3Y2HOFiHOZf/WH0OWR1g9FwDMChrSg2cJtKykxiUqWKkkl+bAM4eLFS/xF9hX3MsRNeVwvXrzIJBwk2igO44KCMg7UWIOD/fYya60gdpA8AswTR/hFCWizJUoUF9uuIUz0f4XtwGgXTIR0/NYrXr5Au2gLtl3pn0kqnW3CwewLDA07qwFdcPNMiFdp8KM7KLwoywf+c5iQs9rcdeXRNpu06fJ5x+/8Nm0ZTmXLh/LCkUo/brpIu7Zdo6IRzM7cX9I1i6rW5EWL6+zflUi1Ghagi+dS6fCBZLETg5BTWSsOK+RLFasG04mjyVQ8IoA9JlLo9PEUPlTz4XYtKlshkEqWCaRf91yjC/FpVDDclyrFhNDJ40l05kSqaNfZMTYzUEzn1YR0iuJ+//aP2qLdG0xRRonXIKVXRSATBAyZuhaxpzMHgCtuKtjrmQru0pDnKd3Uy4mrIYmcIF7HmBzkm8wHZvEn04RgQfSFmXALMcmbPzEEt+SEiw62L8jkeiEuTV7AKFAQb5s58IbmCrvxpXhehLhM4tV0CmFzBkwV0LDRRuIVS4gQbcPOjDfVQPwFwrgcu61hvNkZbkS8amrITrS1rTyLALRLEKA9IM2ejnvXYEjTXE2+KWtPt7dlL+csi0QXGaQc5JCs6+WTPP4w9U3cG66ASn7ohkmwdHSAaNfQXs0P4EBGlIEWCm0WAeaDIiWYRaWcIx/pgAReDsX5BQiUCWaTBerhv2kjONSHQtjGK6YOLg/zRREmeSnH8dwOSry5jbj2d9si4InAPKVjoCbPXF0H75ruGreXF1oHk3gImdX1UOWWJ4M0za+COcb33yKBTE3IMIebqPMq7ThM5Y4fx3HmOG6EYF3SPLXlUixHokq8OQKrNqoIKAJZQSCT9SQrzdw2ZR06/G0jrgqqCCgCuY6AZyU710XJKx0q8eaVmdRxKAI5hUAG8Sr/Zg1gmI49afJKvFnDUksrAvkKAdhOQR74n/HiXb4a//86WGCFn6QEfq6HsmhTbbz/K7JaTxHIBwgEBPqxjzD/MDgzCK5w//KkxeUDOG5qiCDdYH6xI+FiCr8Ugt+IcOi3dtzUj/emoNRCikD+RWDBvKM0oscRatwz0OGOBWaxs8htAw3L7XC8y7j+L4KbNjzU5QUKP9KTnJROhzan0YeLq/DvABcXrdfudaLE6wE/TVYE8jsCxswA39oVS0/y/7iMN+PyOzKex4/1CLhB0+3cs5SQrrvSSrzuUNE0RUAREAQM+SKCv30GEtZwYwTwCjl+JQ3BjqGpqcRrkNCrIqAIuEUAxIFwW1oXHKLfkk/7W4muAijxuiKicUVAEfCIgCFhjwU0QxC40SKlXg36oCgCisBNI3AjQrnphvJ5QfXjzecPgA5fEVAEch+B/wfD5g4z52zZNQAAAABJRU5ErkJggg==[/img][br][/left][url=https://www.geogebra.org/calculator?examMode=suite]https://www.geogebra.org/calculator?examMode=suite[/url][br]start GeoGebra Calculator Suite in examenmodus. Hierbij kunnen de leerlingen alle rekenkundige toepassingen gebruiken.[br][br][url=https://www.geogebra.org/calculator?examMode=bayern_cas]https://www.geogebra.org/calculator?examMode=bayern_cas[/url][br]start GeoGebra Calculator Suite in een speciale examenmodus voor de Duitse deelstaat Beieren.[br][br][url=https://www.geogebra.org/calculator?examMode=niedersachsen]https://www.geogebra.org/calculator?examMode=niedersachsen[/url][br]start GeoGebra Calculator Suite in een speciale examenmodus voor de Duitse deelstaat Nedersaksen.[br][br][url=https://www.geogebra.org/calculator?examMode=vlaanderen]https://www.geogebra.org/calculator?examMode=vlaanderen[/url][br]start GeoGebra Calculator Suite in een speciale examenmodus voor Vlaanderen.[br][br][br]
[table] [tr][br] [td][b][center]Wat[/center][/b][/td][br] [td][b][center]Link[/center][/b][/td][br] [td][b][center]Configuratiesleutel[/center][/b][/td][br] [td][b][center]Hash[/center][/b][/td][br][/tr][br] [tr][br] [td]Beperkt [br]Grafisch[/td][br] [td][url=https://www.geogebra.org/graphing?examMode=graphing]https://www.geogebra.org/graphing[/url][br][url=https://www.geogebra.org/graphing?examMode=graphing]?examMode=graphing[/url][br][/td][br] [td]d13a012250fe725cb9dac545f0b0af6efd3[br]97b3b2a77b5e28448a927fb155df2[br][justify][/justify][/td][br] [td][code]746c0e52[/code][br][br][br][/td][br][/tr][br] [tr][br] [td]Suite: Kies[/td][br] [td][url=https://www.geogebra.org/calculator?examMode=choose]https://www.geogebra.org/calculator[/url][br][url=https://www.geogebra.org/calculator?examMode=choose]?examMode=choose[/url][/td][br] [td]0e3cce08df781108c27729de7217abd29f[br]7de2d8473fcb393a926982e8b8d4f0[br][justify][/justify][/td][br] [td][code]da651d95[/code][br][br][br][/td][br][/tr][br] [tr][br] [td]Suite: Suite[/td][br] [td][url=https://www.geogebra.org/calculator?examMode=suite]https://www.geogebra.org/calculator[/url][br][url=https://www.geogebra.org/calculator?examMode=suite]?examMode=suite[/url][br][/td][br] [td]4b2d5908c8da2b235e9e2083435d6b02d2[br]c1976303a1af40c45ca9faf8c3dac7[br][br][/td][br] [td][code]2d2889b2[/code][br][br][br][/td][br][/tr][br] [tr][br] [td]Suite: [br]Beieren_cas[/td][br] [td][url=https://www.geogebra.org/calculator?examMode=bayern_cas]https://www.geogebra.org/calculator[/url][br][url=https://www.geogebra.org/calculator?examMode=bayern_cas]?examMode=bayern_cas[/url][br][/td][br] [td]2281129519bce0cc5a06f381f2261bf8f0b6[br]d61d9b4cf69a7b81b090ebc99419[br][br][/td][br] [td][code]584447e8[/code][br][br][br][/td][br][/tr][br] [tr][br] [td]Suite: [br]Nedersaksen[/td][br] [td][url=https://www.geogebra.org/calculator?examMode=niedersachsen]https://www.geogebra.org/calculator[/url][br][url=https://www.geogebra.org/calculator?examMode=niedersachsen]?examMode=niedersachsen[/url][/td][br] [td]bb90ce60ff24307b84148db439fc7f48c789[br]c817e38d289ab34275052170e043[br][br][/td][br] [td][code]a1f07791[/code][br][br][br][/td][br][/tr][br] [tr][br] [td]Suite: [br]Vlaanderen[/td][br] [td][url=https://www.geogebra.org/calculator?examMode=vlaanderen]https://www.geogebra.org/calculator[/url][br][url=https://www.geogebra.org/calculator?examMode=vlaanderen]?examMode=vlaanderen[/url][/td][br] [td]8458a0caba270e8143587cf4e0b2569fb3b[br]3f9cbfc3fd188a51600422bd812f5[br][justify][/justify][/td][br] [td][code]625cf893[/code][br][br][br][/td][br][/tr][br][/table]