Medianele unui triunghi.

[b][color=#741b47]Folosiți aplicația următoare pentru a rezolva sarcinile de mai jos! In acest fel veți descoperi ce proprietăți mai au medianele unui triunghi![/color][/b]

[i][b][color=#9900ff]* Construiți un triunghi ABC cu ajutorul instrumentului [/color][color=#ff00ff]poligon[/color][color=#9900ff] .(după selectare faceți 3 clik-uri pentru cele trei vârfuri A, B, C și apoi din nou pe A pentru închiderea poligonului)[/color][/b][/i]

[b][color=#ff7700]Reamintim! Mediana unui triunghi este segmentul care unește vârful unui triunghi cu mijlocul laturii opuse.[/color][/b] [br][b][color=#9900ff]* Pentru a construi o mediană avem nevoie de mijlocul laturilor.[/color][/b](dacă ați uitat cum se construiește mediana, revedeți lecția [url=http://invatamate.com/Lectii/Clasa6/medianaprop1.html]Mediana unui triunghi[/url]) [b][i][color=#9900ff]Redenumiți mijloacele astfel M mijlocul lui BC, N mijlocul lui AB și P mijlocul lui AC.[/color][/i][/b]

[b][i][color=#9900ff]* Acum mai trebuie să uniți printr-un segment vârful A și mijlocul M, vârful B și mijlocul P, vârful C și mijlocul N. (Alegeți instrumentul [/color][color=#ff00ff]segment[/color][color=#9900ff] și dați clik pe punctele vârf și mijloc)[/color][/i][/b]

[i][color=#00ff00][size=100][size=150]Ați construit astfel cele trei mediane ale triunghiului. Modificați forma triunghiului. Ceputeți spune despre cele trei mediane?[/size][/size][/color][/i]

Medianele se intersectează în același punct Medianele sunt congruente Medianele nu se intersectează

[color=#3c78d8][b]Personalizare! Puteți colora triunghiul , laturile și punctele. Pentru aceasta selectați cu ajutorul instrumentului selecție elementul pe care vreți să îl personalizați și din meniul cu proprietăți selectați ce culoare vreți.[/b][/color]

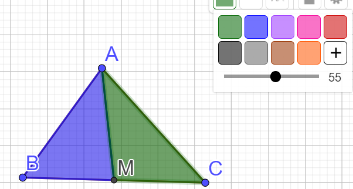
[b][i][color=#9900ff]* Cu instrumentul [/color][color=#ff00ff]intersecție[/color][color=#9900ff] vom construi un punct acolo unde cele trei mediane se intersectează. Selectați instrumentul intersecție și apoi clik pe două dintre mediane.[/color][/i][/b]

[b][i][color=#9900ff]* Vom renota acest punct de intersecție cu G. Acest punct se numește ”centru de greutate” al triunghiului.[/color][/i][/b]

[size=150][color=#00ff00][i]Unde se află centrul de greutate dacă triunghiul este ascuțitunghic?[/i][/color][/size]

În interiorul triunghiul Într-un vârf al triunghiului În exteriorul triunghiului Pe o latură a triunghiului

[size=150][color=#00ff00][i]Unde se află centrul de greutate dacă triunghiul este dreptunghic?[/i][/color][/size]

În exteriorul triunghiului În interiorul triunghiul Pe o latură a triunghiului Într-un vârf al triunghiului

[size=150][color=#00ff00][i]Unde se află centrul de greutate dacă triunghiul este obtuzunghic?[/i][/color][/size]

Pe o latură a triunghiului În exteriorul triunghiului Într-un vârf al triunghiului În interiorul triunghiul

[b][i][color=#9900ff]* În continuare vă propun să măsurați segmentele AG și GM. Pentru aceasta selectați instrumentul [/color][color=#ff00ff]distanță [/color][color=#9900ff]și apoi clik pe punctul A și pe punctul G. Astfel ați obținut lungimea segmentului AG. Clik pe G și apoi pe M. Astfel ați obținut lungimea segmentului GM.[/color][/i][/b]

[size=150][color=#00ff00][i]Care este raportul dintre AG și GM?[/i][/color][/size]

[math]\frac{2}{1}[/math] [math]\frac{2}{3}[/math] [math]\frac{1}{3}[/math] [math]\frac{3}{2}[/math] [math]\frac{1}{2}[/math]

[size=150][color=#00ff00][i]Care este raportul dintre AG și AM?[/i][/color][/size]

[math]\frac{3}{2}[/math] [math]\frac{2}{3}[/math] [math]\frac{1}{3}[/math] [math]\frac{2}{1}[/math] [math]\frac{1}{2}[/math]

[size=150][color=#00ff00][i]Care este raportul dintre GM și AM?[/i][/color][/size]

[math]\frac{1}{3}[/math] [math]\frac{2}{1}[/math] [math]\frac{2}{3}[/math] [math]\frac{3}{2}[/math] [math]\frac{1}{2}[/math]

[size=150][color=#00ff00][i]Care este raportul dintre GM și AG?[/i][/color][/size]

[math]\frac{3}{2}[/math] [math]\frac{2}{3}[/math] [math]\frac{1}{3}[/math] [math]\frac{2}{1}[/math] [math]\frac{1}{2}[/math]

[i][color=#00ff00][size=150]Bifați propozițiile corecte![/size][/color][/i]

GM este o treime din AM Punctul G se află la o treime din mediană față de latură Punctul G se află la două treimi din mediană față de vârful triunghiului AM este de trei ori mai mare ca AG GM este jumătate din AG AG este de două ori mai mare ca GM

[b][color=#1e84cc]Acum puteți verifica dacă proprietățile descoperite mai sus despre punctul G sunt respectaet și pentru medianele BP și CN![/color][/b]

Medianele unui triunghi.

Information: Medianele unui triunghi.