circles, ovals, ellipses and architecture
We know the circle as an elementary figure that's often used in architecture, sometimes as a cosmic symbol. We know the ellips as a conic and since Kepler also as the orbit planets follow around the sun. Compared with circle and ellipse the oval is the ugly duc. It cannot be described by one equation, we say that baroc architects used ovals as an approximation of an ellips, in books and touristic guides ovals and ellipses are mixed etc. However the history of the oval reads as a fascinating and ancient story. Based on a lot of articles, supplemented by GeoGebra applets I will try to guide you through this story, thanks to some support of some ex colleagues from school.
Table of Contents
- circle
- San Vitale
- The spheres of Ptolemaeus
- central scheme in the renaissance
- A look to Roman Antiquity
- The amphitheater of Verona
- Rome - Colosseum
- oval schemes
- elongating the central scheme
- Serlio 1
- Serlio 2
- Serlio 3
- Serlio 4
- realisations
- Vignola - Sant'Anna dei Palafrenieri
- Capriani - San Giacomo degli Incurabili
- Bernini - Sant'Andrea al Quirinale
- Borromini - San Carlo alle quattro fontane
- Cosmas Damian and Egid Quirin Asam - Weltenburg
- Bathasar Neumann - Vierzehnheiligen
- ellipse
- ellipse as a flat curve
- ellipse in 3d
- Dandelin's spheres
- Dürer
- Dürer 2
- da Vinci and others
- ovals, ellipses, the Saint Peters Square and a coffee can
- oval and ellipse
- perpendicular lines to an oval and an ellipse
- Bernini - St Peters Square (1656)
- St Peters Square as an ellipse...
- coffee pot
- links
- link with Kepler?
- Link with Carolus Borromeus?
- links
San Vitale
cosmologic references
The early-christian basilic of San Vitale (526-547) in Ravenna shows clear cosmologic references in the cross vault and the abse. [br]In the apex of the cross vault a lamb is depicted in a blue sky full of stars, sustained by four angels.[br]In the abse mozaic Christ is sitting on a blue mandorla, as the ruler of the universe.
The amphitheater of Verona
In th artikel [url=https://www.researchgate.net/publication/277908088_Baroque_Oval_Churches_Innovative_Geometrical_Patterns_in_Early_Modern_Sacred_Architecture]Baroque Oval Churches: Innovative Geometrical Patterns in Early Modern Sacred Architecture[/url] Sylvie Duvernoy describes how well-known renaissance architects as Giovanni Battista da Sangallo, Baldassare Peruzzi, Sebastiano Serlio and Andrea Palladio studied the amphitheaters of Verona and Rome. Based on this studies they described how to design oval shaped buildings.[br][br][size=150]circumference[/size][br]The Roman designers had to design the building so that they could devide the circumpherence into equal arches to be used as the entrances for the public.[br]De length l of a circular arch can be written as:[br]l = 2 x [math]\pi[/math] x R x [math]\alpha[/math]/360° (with R as the radius and [math]\alpha[/math] as the angle of the circular arch.[br]The drawings of Peruzzi show that in the amphitheater of Verona each circular arch contains 18 arches. In other words: the four circular arches have an equel lenght.[br][br][size=150]radii and angles[/size][br][size=100]What are the radii R1 and R2 and the angles [math]\alpha[/math]1 en [math]\alpha[/math]2 of the circular arches in Verona?[br]With equal circular arches in a symmetric oval, one can write:[br]2 x [math]\pi[/math] x R1 x [math]\alpha[/math]1 = 2 x [math]\pi[/math] x R2 x [math]\alpha[/math]2 and [math]\alpha[/math]1+ [math]\alpha[/math]2 = 180°[br][/size]thus: R1 x [math]\alpha[/math]1 = R2 x [math]\alpha[/math]2 and [math]\alpha[/math]1+ [math]\alpha[/math]2 = 180°[br]finally: R1/R2 = [math]\alpha[/math]2/[math]\alpha[/math]1[br][br][size=100]In Verona Peruzzi found the ratio R1/R2 = [math]\alpha[/math]2/[math]\alpha[/math]1 = 5/3.[br]5/3 is a classic ratio known as [i]superbipartiens tertias[/i] (tertius).[/size]
elongating the central scheme
Renaissance architects were familiar to oval schemes for they studied the amphitheaters in Rome and Verona. Architects as Baldassare Peruzzi (1481 - 1536) and his pupil Sebastiano Serlio (1475 - 1536) studied ancient monuments and in the first of his 7 books Serlio describes some basic constructions to design oval shapes.
design
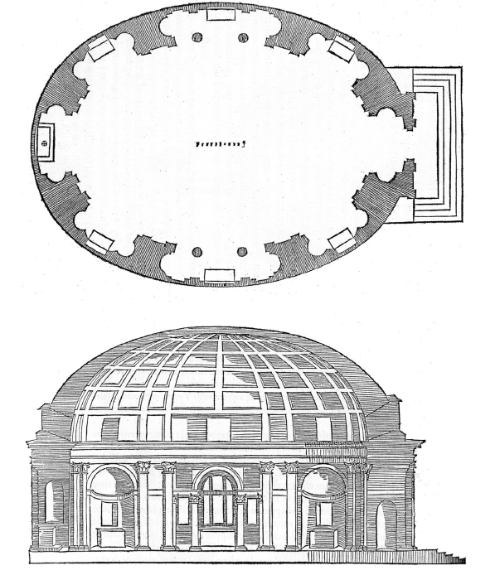
In his fifth book [i]Le diverse Forme dei Tepli Sacri[/i] Serlio draws a desing of his own for an oval church that looks like an elongated version of the Pantheon.
Vignola - Sant'Anna dei Palafrenieri
elongated central plan
During the 15th century renaissance central plans were very pompular. Mid 16th century Jacopo Barozzi da Vignola (1507-1573) introduced a new interpretation by elongating the central space. He and his followers were the first to design and build churches with oval plans.[br]During the counter reformation a lot of new religious congregations were founded. As abbeys in the middle ages gave a boost to the roman style and Bourgundy in France became a lab for religious art, Rome became a lab for religious architecture in 16th and 17th century.
first realisations
For the Gesu church in Rome Vignola first designed a church with an oval plan, but eventually it was rejected and the Gesu church was realised with a classic rectangular nave and a circular dome.[br]At the border of the Vatican and the city of Rome Vignola could realise the first oval church: Sant'Anna dei Palafrenieri for the fraternity of the papal grooms'. The works began in 1572, one year before Vignola's death and was finished by his son.[br]Briefly afte this Francesco Capriani da Volterra (1535–1594), a pupil of Vignola, designed the second oval church in Rome: San Giacomo degli Incurabili.[br][url=https://www.researchgate.net/publication/277908088_Baroque_Oval_Churches_Innovative_Geometrical_Patterns_in_Early_Modern_Sacred_Architecture]Sylvie Duvernoy[/url] writes that every church is different, but at the same time a variation on the same principles.[br]You can describe anu oval by the ratio of its axes and the place of its centers. Hereby more schemes were used than described by Serlio.[br]For example Vignola designed Sant'Anna dei Palafrenieri starting from Pythagorian 3-4-5-triangles, while Capriano used equilateral triangles (= Serlio 4).[br][br]
ellipse as a flat curve
locus
a locus is a geometric figure containing a set of points matching a specific condition.[br]For example: [br][list][*]the perpendicular bisecor of two points is the locus of the points at the same distance from two given points.[/*][*]the circle is the locus of twe points at the same distance from a given point.[br][/*][*]the bisector of two intersecting lines is the locus of the points at the sams distance from two given lines.[/*][/list]
ellipse as a locus
Een ellips is the locus of a point which moves in a plane such that the sum of its distances from two given points (called foci) add up to a constant.[br]This means you can draw an ellips with the help of a rope: Put down two stakes and loop a piee of rope around them. Pull the loop taut and mark the points aroud a curve.
applet
The method is illustrated in the applet below.[br][list][*]Drag the point F[sub]1[/sub] and define the distance between the two foci. [/*][*]Drag the point C and define the lenghts of the rope.[/*][*]Drag teh point Pand draw the ellipse.[/*][/list]
gardener's method
This construction is called [i]the gardener's method[/i] because it was used in Engelse gardens to mark flowerbeds. Architects and military ingeneers mention it in tractates.[br]E.g. Ambroise Bachot mentions the methode in his book from 1598 on architecture, fortifications and weapons of war.
oval and ellipse
epilogue of a conflict
We can't blame Serlio and his renaissance contemporaries. There wasn't an equation for an ellipse yet, since analytic geometry was introduced only in the 17th century. [br]However despite what's known in mathematics the abiguity and confusion remains until now. In the article [url=https://www.researchgate.net/publication/328307082_ELLIPSES_AND_OVALS_IN_THE_PHYSICAL_SPACE_OF_ST_PETER'S_SQUARE_IN_ROME]Ellipses and ovals in the physical space of St.Peter's square in Rome[/url] autors Alessandra Carlini and Paola Magrone write:[br]"[i]An ambiguity of use use between the terms ellipse and oval remains in some kind of literature, as toutistic literature and some school textbooks. For exemple, the Coliseum and the plan od St Peter's square are both described als elliptical shaped. Moreover, in thouristic guids (in the fout we consulted) St Peter's square is described al elliptical[/i]". [br]The autors also quote the bestseller book 'Angels and Demons' by Dan Brown:[br]"[i]Two fountains flanked the obelisk in perfect symmetry. Art historians knew the fountains marked the exact geometric focal points of Bernini's elliptical piazza, but it was an architectural oddity Langdon had never really considered unti today. It seemed Rome was suddenly filled with ellipses, pyramids and startling geometry[/i]".[br][br]Talking about ambiguity and confusion I can confirm what the autors write. In all kinds of touristic guides and even books on architecture ovals and ellipses are mixed together. In one the tourist is encouraged to place himself upon the round stones in St Peter's Square that indicate the centre of the colonnade and lok towards the colonnade. These stones mark the foci of the ellipsoid square, says the guide...[br]In some books on architecture you read about ovals and on the next line about 'elliptic shapes'.[br]In his artikel [url=https://www.academia.edu/1130844/Ellissi_e_ovali_Epilogo_di_un_conflitto]Ellissi e ovali, epilogo di un conflitto[/url] Riccardo Miglari focusses on this matter and with the word 'epilogue' in the title he makes clear that as far as he's concerned the discussion is finished.[br]According to him the solutions is not to be found in measuring but in building traditions and literature, both of them very clear.
an inevitable discussion
Migliari calls the discussion inevitable, referring to humanist autors, who were using both names wrongly and mixed together. Pietro Cataneo describes the construction of a curve using a rope and calls it 'figure ovale'. Vincenzo Scamozzi explains the construction of an curve 'the Greek call ellipse'... but draws an oval. [br]Migliari continuous: "Therefore I'm inclined to accept the promiscuity of our two curves whitin this discussion. But in a contemporary technical-scientifical context the two names stand for curves that are far apart, not only by their origin, but also by their appearance, so you can't be an architect or ingeneer and not distinguish both." He continuous: "It's important for me to add that I'm not willing to award a primacy of intellectual nobility to the ellipse an oval wouldn't have.[br]Yes, the ellipse is a cone, the planets follow an elliptical orbit , the ellipse was described throughout the ages from Apollonius to Dessargues. The ovaal has got a more modest origin. It's just a concatenation of circular arcs that's in its practical use more interessanting than mathematical theory.[br]According to some because it's easier to construct than an ellips, especially in large dimensions.[br]But on closer inspection in architecture in fact the oval is the most interesting option."[br]But how can you draw these curves?[br]
an oval that looks almost an ellipse
[list][*]Construct two circles with equal radius as in the figure below.[/*][*]Draw a line starting from the intersection points of the two circles through the center of the circles and define the other intersection point with the circle.[br][/*][*]Now compose the oval out of two green circular arcs with the green centers and two red circular arcs with the red centers.[/*][*]Define r as half the long axis of the oval.[/*][/list]
an ellipse that looks almost an oval
Select the checkbox and show the ellipse with the same axes as the oval.[br]Construct the ellipse as follows:[list][*]Mark the intersection point of the vertical axis and the oval.[/*][*]Draw a circle with radius r and center this intersection point.[br][/*][*]Define the foci F1 and F2 as the intersection points of the circle and the long axis of the oval.[/*][*]Create the ellipse with foci F1 and F2 and long axis 2r.[/*][/list]Notie the minimal difference between oval and ellipse.[br]Only at an angle of [math]\approx[/math] 45° from the centers of both small circles there's a little difference. For exemple the St-Peter's Square, with a log axis of 240 m the maximum difference is just 1,6 m and for the greatest part of both curves the difference is almost negligible. Of course the little difference doesn't help to dispel the misconception the square is elliptical.
link with Kepler?
renaissance versus baroc
It is tempting to characterise art movementss ans tyles with features that are easy to distinguish. Doing so the renaissance style is often linked to the circle, baroc to the ellipse.
renaissance and the cirkel
The Uomo Vitruviano van Leonardo da Vinci is nice coat reck for renaissance.[br]One drawing refers to Antiquiti, as well as to the circle as perfect basic figure and to Leonardo da Vinci as the personaliaation of the renaissance.
baroc and ellipse
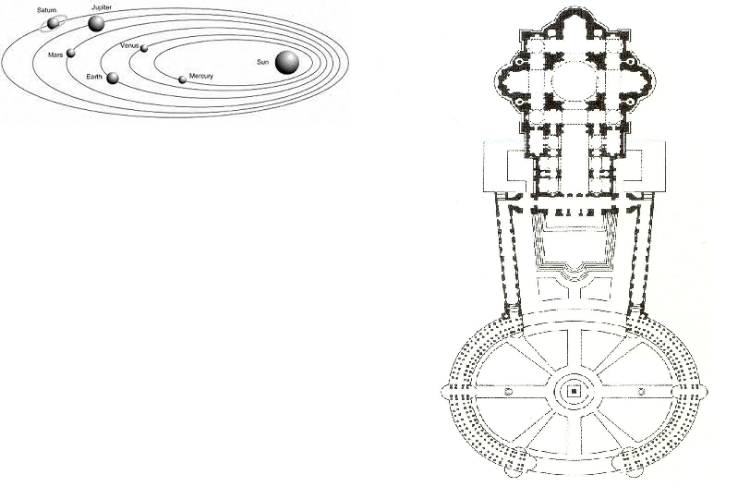
The opposite of the Uomo Universale of da Vinci stands the tandem Bernini-Kepler as iconic contrast.[br]da Vinci is looking back to Antiquity, Bernini joins the scientific revolution of Kepler's worldview and resolutely prefers the ellips. and for St Peters Square supplies the ideal picture.
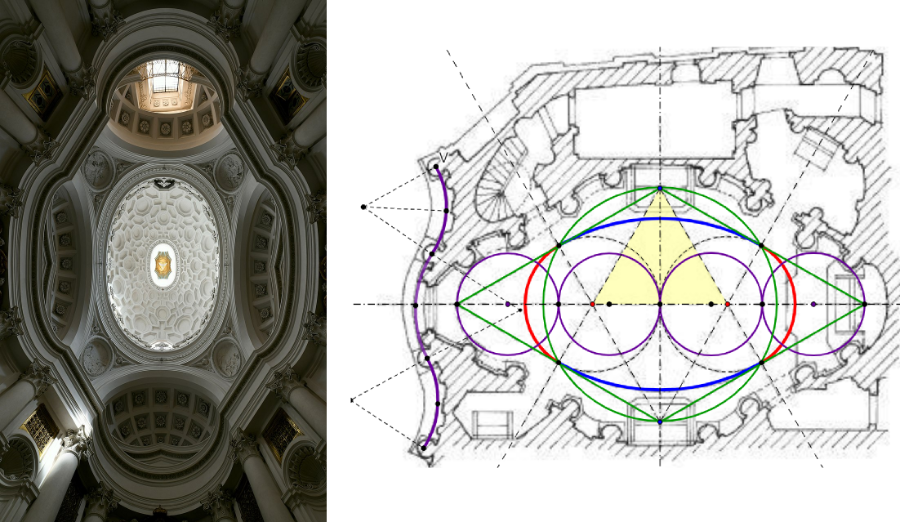
Unfortunately for one who loves clear contrasts, is reality history is much more fluid than this. [br]In fact the people that studied the oval shape of the Roman amphiathers and designed the first oval schemes themselves were renaissance architects as Sebastiano Serlio (1475-1554). And the first oval churches of Vignola (1507-1573) and Capriano (1535-1594) date from before Kepler's publication in 1609. Even without speaking about practivcle advantages of ovals, analyzing the plans it's obvious that dat architects as Bernini and Borromini stood in a building tradition that was familiar with the use of circles and ovals and just enriched and developed this tradition.[br]An autor as Valerie Shrimplin emphasizes the cosmic interests of Borromini and links both [url=https://www.valerieshrimplin.com/pdfs/20190622-kepler-borromini-and-harmonices-mundi-wide-ppt.pdf]Borromini en Kepler[/url], but it's unlucky that she expicitely points to Borromini's masterpiece San Carlo alle Quattro Fontane, an excellent exemple of the possibilities of circles and ovals and therefore not even an ellipse.[br]A picture of the dome of this church is clearly identificable as an oval.
