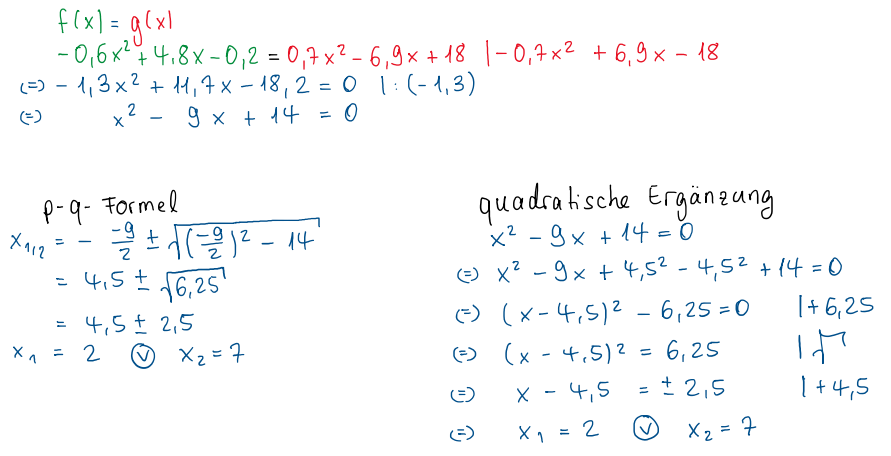
Auswertung der Einstiegsaufgabe
Schrittweise Bestimmung der Fläche zwischen zwei Graphen
Im Folgenden wird nun dargestellt, wie die [b]Fläche zwischen den beiden Funktionen [/b]und schrittweise bestimmt wird.
Klicke im linken Teil der Grafik auf die schwarzen Kreisringe, um dir die notwendige Fläche anzuzeigen, bzw. sie wieder auszublenden.
Bei der Betrachtung der Fläche zwischen den beiden Funktionen fällt auf, dass sie links und rechts durch die Schnittpunkte der beiden Funktionen beschränkt ist. Weil diese beiden Schnittpunkte die Grenzen der Flächen - also der Integrale - sind, müssen sie berechnet werden.[br][br]An den Schnittpunkten liegen beide Funktionen an dem gleichen Punkt. Wollen wir diese Stelle also bestimmen, müssen wir berechnen, wo die Funktionsgleichungen die gleichen Werte annehmen. Dafür nutzen wir (wie bei der Schnittpunktbestimmung von Geraden) das Gleichsetzungsverfahren. Anschließend wird nach 0 umgestellt und die Lösung der Gleichung bestimmt.[br][br]Zeichnet man die Flächen unterhalb der Funktionen bis zur x-Achse in den Grenzen der Schnittstellen ein, so fällt auf, dass sich diese Flächen in einem Bereich überdecken. Im anderen Bereich wird die Fläche ausschließlich durch die Fläche unter einer Funktion bestimmt. Diese Fläche ist dabei genau die Fläche zwischen den beiden Funktionen. Da wir genau hieran interessiert sind, muss von der größeren Fläche die kleinere Fläche abgezogen werden. Übrig bleibt dann nur noch die Fläche zwischen den beiden Funktionen.
Zusammenfassend lassen sich also vier Schritte aufstellen:[br][list=1][*]Funktionen gleichsetzen, um Schnittstellen zu berechnen ([math]f\left(x\right)=g\left(x\right)[/math])[/*][*]Fläche unter der ersten Funktion im Bereich der Schnittstellen bestimmen.[/*][*]Fläche unter der zweiten Funktion im Bereich der Schnittstellen bestimmen.[/*][*]Kleine Fläche von der größeren Fläche subtrahieren.[/*][/list][br]Diese Schritte werden im Folgenden beispielhaft gezeigt:
[b]Schritt 1:[/b] [br]Zunächst müssen die Schnitt[b]stellen[/b] von [math]f[/math] und [math]g[/math] bestimmt werden, damit wir unsere [b]Integralgrenzen[/b][br]erhalten.[br]
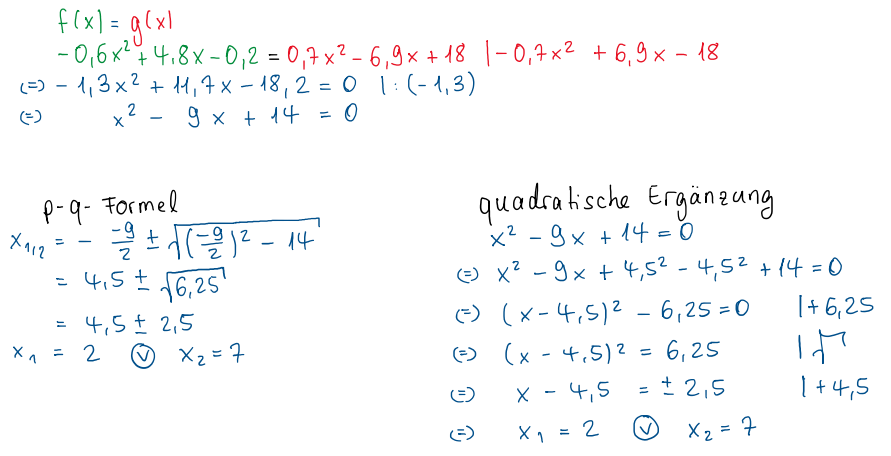
[b]Schritt 2:[br][/b]Bestimme die [b]Fläche [/b]unter der Funktion [math]f[/math] im Bereich von 2 bis 7. Bilde dazu zunächst die Stammfunktion von [math]f[/math].[br][br][br]
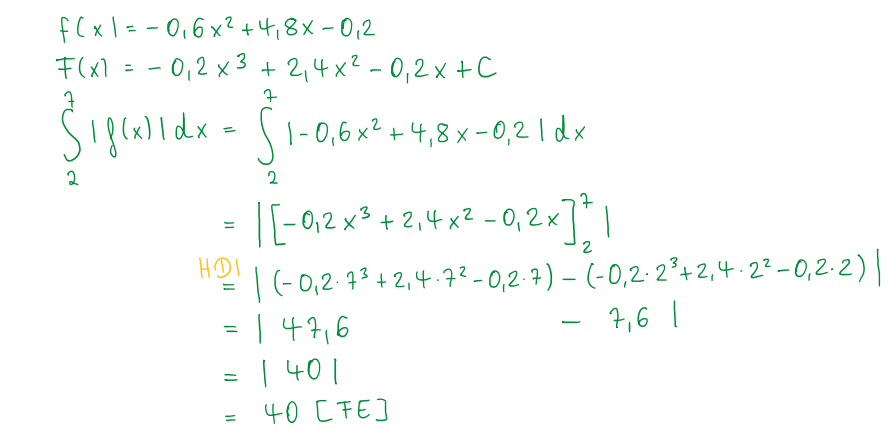
[b]Schritt 3:[/b] [br]Bestimme die [b]Fläche [/b]unter der Funktion [math]g[/math] im Bereich von 2 bis 7. Bilde dazu zunächst die Stammfunktion von [math]g[/math].[br][br][br]
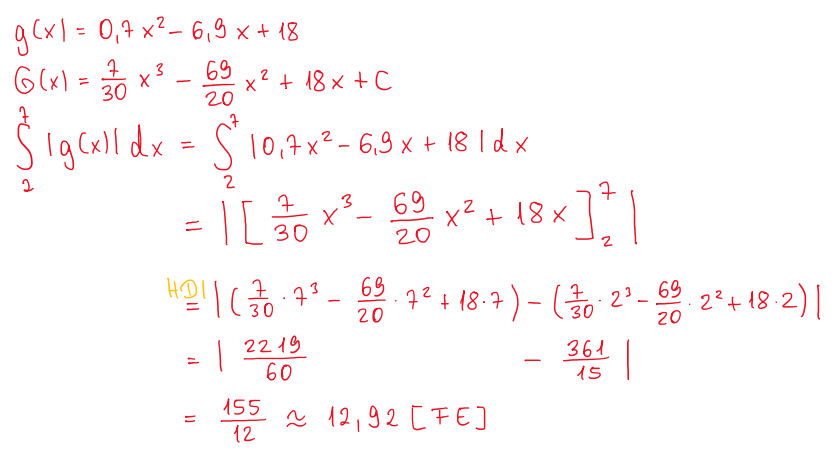
[b]Schritt 4:[/b] [br]Bestimme die [b]Fläche [/b]zwischen den beiden Funktionen [math]f[/math] und [math]g[/math] im Bereich von 2 bis 7. Subtrahiere dazu die kleinere von der größeren Fläche, das heißt die Fläche von [math]g[/math] wird von der Fläche von [math]f[/math] abgezogen. [br][br][br]

[b]Ergebnis:[/b] [br]Die Fläche, die von [math]f[/math] und [math]g[/math] eingeschlossen wird, beträgt [b]27,08 Flächeneinheiten[/b].
